五年级下册数学青岛版(五四学制)圆的周长课件(23张PPT)
文档属性
| 名称 | 五年级下册数学青岛版(五四学制)圆的周长课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
圆一周的长度就是圆的周长
复习导入
圆的周长和我们以前学习的周长有什么不同之处?
探究新知
小组合作探究
1.四人一小组利用手中的工具测量圆的周长。
2.相互说一说,你是怎样测量的。
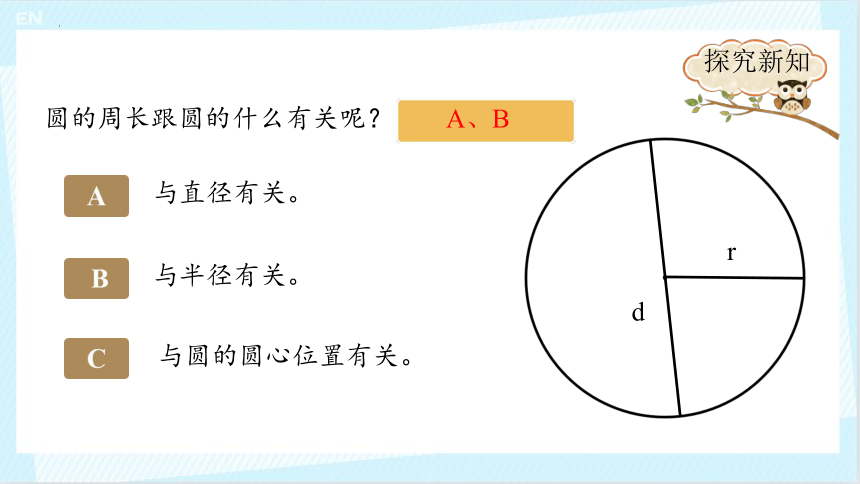
圆的周长跟圆的什么有关呢?
与直径有关。
与半径有关。
与圆的圆心位置有关。
r
d
探究新知
A、B
探究新知
圆的周长跟圆的半径、直径有关
正方形的周长=边长×4
d的倍数
小组合作,算出周长和直径的比值,把结果填入下表中,看看有什么发现。
探究新知
探究新知
探究新知
圆的直径和周长存在着哪种关系?
圆的周长和直径的比值不是固定的值。
圆的周长和直径的比值是固定的值,大约是3.14。
圆的周长和直径的比值就是3.14。
B
探究新知
周长
∶
直径
=
固定比值
3.1415926535……
圆周率
无限不循环小数
圆周率
3.1415926535……
探究新知
总结圆的周长公式:
上层直径30米
祭天台上层圆台周长是多少米?
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
天坛主要由圜丘和祈谷(祈年殿)两坛组成。
圜丘坛俗称祭天台,共有三层。上层圆台直径30米,中层直径50米,下层直径70米。
祈年殿殿顶周长是100米。
祈年殿殿顶周长是100米
祈年殿殿顶的
直径是多少米?
2
中层直径50米
下层直径70米
二、合作探索
3.14×30=94.2(米)
答:祭天台上层的周长是94.2米。
祭天台上层的周长是多少?
二、合作探索
祈年殿殿顶的周长是100米,它的直径是多少米?
解:设祈年殿殿顶的直径是χ米。
χ×3.14=100
χ×3.14÷3.14=100÷3.14
χ≈31.85
答:祈年殿殿顶的直径约是31.85米。
除不尽时,
得数一般保留两位小数。
试一试
3.14×20
=62.8(cm)
求下面各圆的周长。
20cm
4dm
80mm
3m
3.14×(4×2)
=25.12(dm)
3.14×80
=251.2(mm)
3.14×(3×2)
=18.84(m)
三、自主练习
3.14×(1.2×2)
=3.14×2.4
=7.536(米)
答:绕石碾走一圈大约是7.536米。
3.
三、自主练习
时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
3.14×(12×2)
=3.14×24
=75.36(厘米)
3.14×(18×2)
=3.14×36
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
4.请将表格补充完整。(单位:米)
三、自主练习
三、自主练习
7.85÷3.14=2.5(cm)
2.5cm<2.6cm
答:这个储钱罐能放进一元的硬币。
6.火眼金睛辨对错。
三、自主练习
(1)圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。( )
(2)圆的周长与它直径的比的比值是π。 ( )
(3)两圆半径的比是2:1,则其周长的比是4:1 ( )
(4)用4个圆心角都是90°的扇形一定可以拼成一个圆。 ( )
×
×
×
√
(5)半圆的周长就是圆周长的一半。 ( )
×
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,
需要增加多长的篱笆?
三、自主练习
(1)3.14×5÷2
=15.7÷2
=7.85(米)
答:需要7.85米篱笆。
(2)3.14×(5+2)÷2
=21.98÷2
=10.99(米)
10.99-7.85=3.14(米)
答:需要增加3.14米篱笆。
7.如图,依墙而建的鸡舍围成半圆形,其直径为5米。
三、自主练习
1.57×40÷3.14÷2
=62.8÷3.14÷2
=20÷2
=10(米)
答:这个水池的半径是10米。
三、自主练习
.
.
85.39m
3.14×73+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
道的示意图。跑道的一周是
多少米?
9.右面是一个国际标准田径跑
回顾今天所学内容,完成填空。
课堂总结
圆一周的长度就是圆的周长
复习导入
圆的周长和我们以前学习的周长有什么不同之处?
探究新知
小组合作探究
1.四人一小组利用手中的工具测量圆的周长。
2.相互说一说,你是怎样测量的。
圆的周长跟圆的什么有关呢?
与直径有关。
与半径有关。
与圆的圆心位置有关。
r
d
探究新知
A、B
探究新知
圆的周长跟圆的半径、直径有关
正方形的周长=边长×4
d的倍数
小组合作,算出周长和直径的比值,把结果填入下表中,看看有什么发现。
探究新知
探究新知
探究新知
圆的直径和周长存在着哪种关系?
圆的周长和直径的比值不是固定的值。
圆的周长和直径的比值是固定的值,大约是3.14。
圆的周长和直径的比值就是3.14。
B
探究新知
周长
∶
直径
=
固定比值
3.1415926535……
圆周率
无限不循环小数
圆周率
3.1415926535……
探究新知
总结圆的周长公式:
上层直径30米
祭天台上层圆台周长是多少米?
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
天坛主要由圜丘和祈谷(祈年殿)两坛组成。
圜丘坛俗称祭天台,共有三层。上层圆台直径30米,中层直径50米,下层直径70米。
祈年殿殿顶周长是100米。
祈年殿殿顶周长是100米
祈年殿殿顶的
直径是多少米?
2
中层直径50米
下层直径70米
二、合作探索
3.14×30=94.2(米)
答:祭天台上层的周长是94.2米。
祭天台上层的周长是多少?
二、合作探索
祈年殿殿顶的周长是100米,它的直径是多少米?
解:设祈年殿殿顶的直径是χ米。
χ×3.14=100
χ×3.14÷3.14=100÷3.14
χ≈31.85
答:祈年殿殿顶的直径约是31.85米。
除不尽时,
得数一般保留两位小数。
试一试
3.14×20
=62.8(cm)
求下面各圆的周长。
20cm
4dm
80mm
3m
3.14×(4×2)
=25.12(dm)
3.14×80
=251.2(mm)
3.14×(3×2)
=18.84(m)
三、自主练习
3.14×(1.2×2)
=3.14×2.4
=7.536(米)
答:绕石碾走一圈大约是7.536米。
3.
三、自主练习
时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
3.14×(12×2)
=3.14×24
=75.36(厘米)
3.14×(18×2)
=3.14×36
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
4.请将表格补充完整。(单位:米)
三、自主练习
三、自主练习
7.85÷3.14=2.5(cm)
2.5cm<2.6cm
答:这个储钱罐能放进一元的硬币。
6.火眼金睛辨对错。
三、自主练习
(1)圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。( )
(2)圆的周长与它直径的比的比值是π。 ( )
(3)两圆半径的比是2:1,则其周长的比是4:1 ( )
(4)用4个圆心角都是90°的扇形一定可以拼成一个圆。 ( )
×
×
×
√
(5)半圆的周长就是圆周长的一半。 ( )
×
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,
需要增加多长的篱笆?
三、自主练习
(1)3.14×5÷2
=15.7÷2
=7.85(米)
答:需要7.85米篱笆。
(2)3.14×(5+2)÷2
=21.98÷2
=10.99(米)
10.99-7.85=3.14(米)
答:需要增加3.14米篱笆。
7.如图,依墙而建的鸡舍围成半圆形,其直径为5米。
三、自主练习
1.57×40÷3.14÷2
=62.8÷3.14÷2
=20÷2
=10(米)
答:这个水池的半径是10米。
三、自主练习
.
.
85.39m
3.14×73+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
道的示意图。跑道的一周是
多少米?
9.右面是一个国际标准田径跑
回顾今天所学内容,完成填空。
课堂总结
