苏教版五年级下册数学第六单元《圆》检测卷(含答案解析)
文档属性
| 名称 | 苏教版五年级下册数学第六单元《圆》检测卷(含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 363.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览



文档简介
五年级数学下册单元检测卷
第六单元《圆》
姓名:_________ 班级:_________ 学号:_________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.答题完成后,请再检查一下哦!
一、选择题
1.一个圆的直径是10cm,如果它的直径扩大为原来的2倍,则扩大后的圆的半径为( )
A.10cm B.5cm C.20cm D.15cm
2.任何圆的周长总是等于它的直径的( )。
A.3倍 B.3.14倍 C.3.1415926倍 D.π倍
3.在一个边长为2厘米的正方形内,画一个最大的圆,这个圆的直径是( )厘米.
A.1 B.2 C.4
4.从12时起,经过( )小时,时针经过的扇形圆心角是150°。
A.4 B.10 C.5 D.3
5.用一张长是7分米,宽2分米的长方形剪出一个最大的圆,像这样的圆最多可以剪( )个。
A.1 B.2 C.3 D.4
6.一个半圆的直径是6厘米,那么这个半圆的周长是( )厘米。
A.3π B.3π+6 C.6π D.6π+6
7.半径3厘米的圆的圆周率( )半径5厘米的圆的圆周率.
A.大于 B.小于 C.等于
8.圆周率π是一个( )。
A.有限小数 B.无限循环小数
C.无限不循环小数 D.以上都不对
二、填空题
9.如图,长方形的宽是4cm,图中阴影部分面积是________cm2
10.如图,将一个半径2厘米的圆形纸片平均分成若干份,剪开后拼成一个近似的长方形,拼成的近似长方形的周长是__________厘米。
11.圆周率是圆的周长与__________的比值,用字母__________来表示;它是一个__________小数,实际应用中一般取它的近似值,即__________。
12.把一个圆平均分成若干份,可以拼成一个近似的长方形,长方形的长相当于圆周长的,宽相当于圆的__________。
13.图中阴影部分的面积__________平方厘米。(单位:厘米)(π取3.14)
14.如图,点__________是圆心,线段__________是半径,线段__________是直径,如果已知OA=3cm,,那么OC=__________cm.,OB=__________cm,BC=__________cm.
三、判断题
15.把一张圆形纸片对折后打开,换个方向再对折.两条折痕的交点就是这个圆的圆心.( )
16.当圆的直径和正方形的边长相等时,正方形的面积比圆的面积大.( )
17.下图中长方形周长是24厘米,半圆面积就是25.12平方厘米。( )
18.一个圆形轮子的半径增加0.5米,那么这个轮子滚一周的长度就增加1米。( )
19.一个圆的半径增加3厘米,直径就会增加6厘米。( )
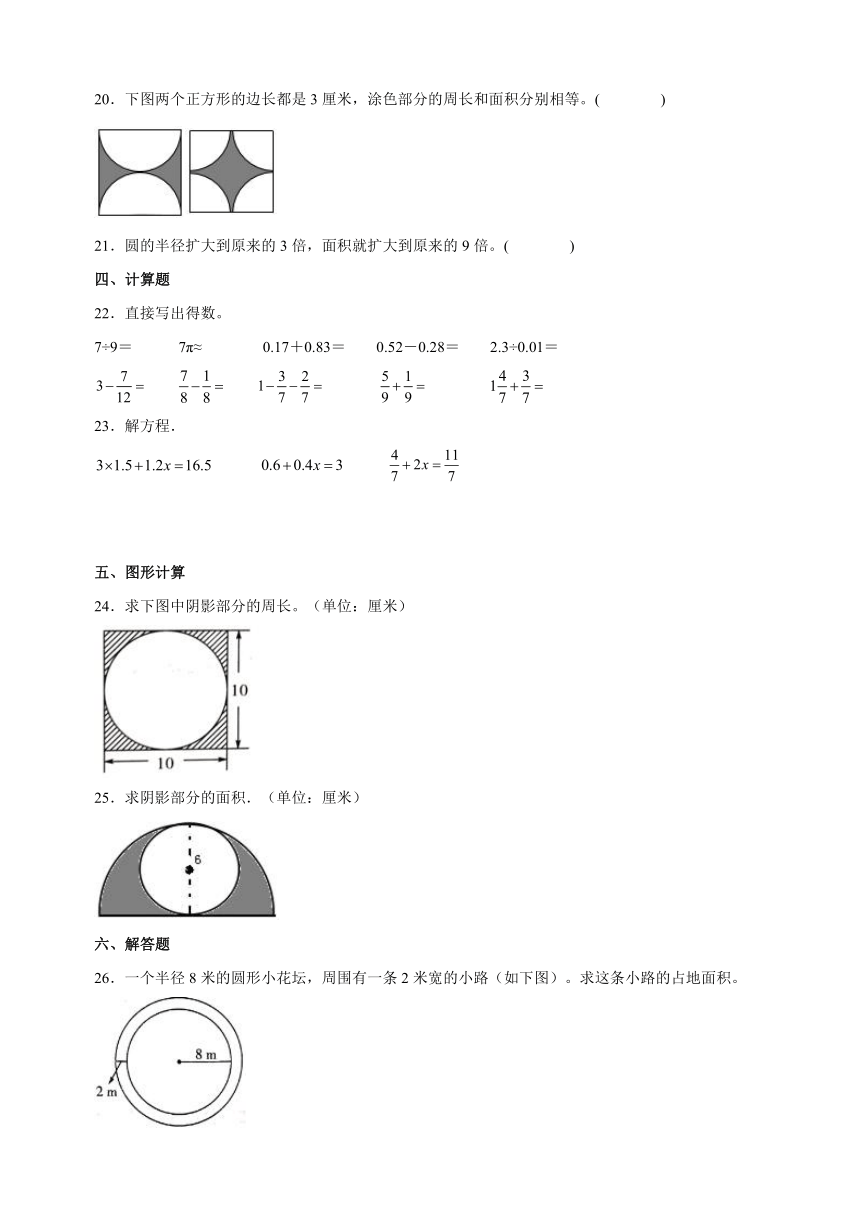
20.下图两个正方形的边长都是3厘米,涂色部分的周长和面积分别相等。( )
21.圆的半径扩大到原来的3倍,面积就扩大到原来的9倍。( )
四、计算题
22.直接写出得数。
7÷9= 7π≈ 0.17+0.83= 0.52-0.28= 2.3÷0.01=
23.解方程.
五、图形计算
24.求下图中阴影部分的周长。(单位:厘米)
25.求阴影部分的面积.(单位:厘米)
六、解答题
26.一个半径8米的圆形小花坛,周围有一条2米宽的小路(如下图)。求这条小路的占地面积。
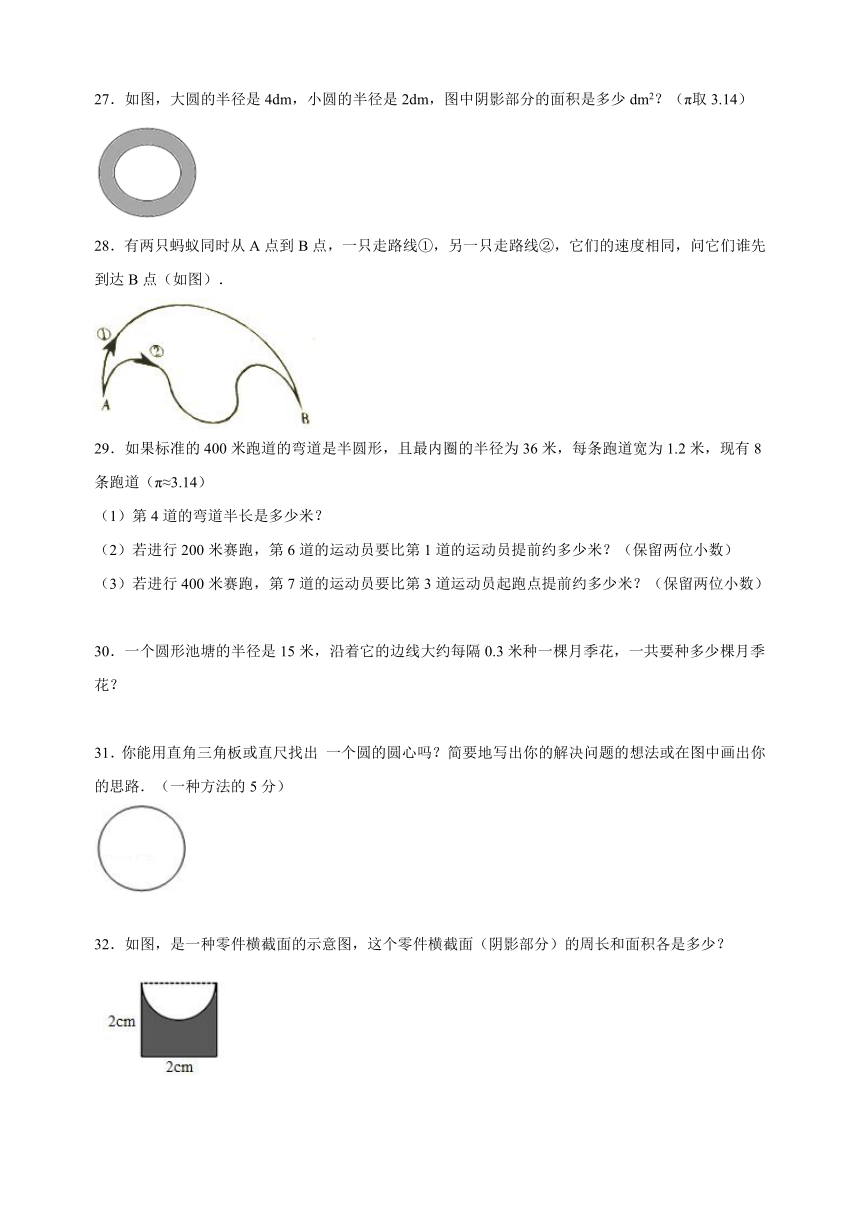
27.如图,大圆的半径是4dm,小圆的半径是2dm,图中阴影部分的面积是多少dm2?(π取3.14)
28.有两只蚂蚁同时从A点到B点,一只走路线①,另一只走路线②,它们的速度相同,问它们谁先到达B点(如图).
29.如果标准的400米跑道的弯道是半圆形,且最内圈的半径为36米,每条跑道宽为1.2米,现有8条跑道(π≈3.14)
(1)第4道的弯道半长是多少米?
(2)若进行200米赛跑,第6道的运动员要比第1道的运动员提前约多少米?(保留两位小数)
(3)若进行400米赛跑,第7道的运动员要比第3道运动员起跑点提前约多少米?(保留两位小数)
30.一个圆形池塘的半径是15米,沿着它的边线大约每隔0.3米种一棵月季花,一共要种多少棵月季花?
31.你能用直角三角板或直尺找出 一个圆的圆心吗?简要地写出你的解决问题的想法或在图中画出你的思路.(一种方法的5分)
32.如图,是一种零件横截面的示意图,这个零件横截面(阴影部分)的周长和面积各是多少?
参考答案
1.A
【详解】试题分析:根据同圆中半径和直径的关系可知“r=d÷2”,进行解答即可。
解:原来圆的直径是l0cm,如果它的直径扩大为原来的2倍,则变成了20cm,根据r=d÷2=20÷2=10(厘米);故选A.
点评:此题考查了同圆中半径和直径的关系。
2.D
【详解】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,即圆的周长是直径的π倍。
故答案为:D。
3.B
【详解】抓住“最大的圆就是直径等于正方形边长2厘米的圆”,即可解决问题。此题关键是根据正方形内最大的圆的特点得出:圆的直径等于正方形的边长。
4.C
【解析】根据题意,因为分针每转一个大格是30°,所以我们用总角度除以30°即可。
【详解】150÷30=5
故答案为:C
【点睛】此题考查学生需要知道在钟表内,分针每转一个大格是30°。
5.C
【详解】试题分析:在一张长是7分米,宽2分米的长方形里面剪最大的圆,应以长方形的宽边为圆的直径剪,看一看长7分米里面有几个2分米即可。
解:以长方形的宽边为圆的直径剪,
最多可以剪:7÷2=3(个)…1;
答:像这样的圆最多可以剪3个。故选C
点评:此题考查在长方形里剪圆的个数,应以宽边为直径剪,再看长边里有几个宽边的长度即可确定圆的个数。
6.B
【解析】半圆的周长是由半圆弧加直径组成,通过圆的周长公式:,求出圆的周长,再除以2,最后加上直径即可解答。
【详解】6×π÷2+6
=6π÷2+6
=3π+6(厘米)
故答案为:B
【点睛】此题关键在于理解半圆的周长是由半圆弧加直径组成。
7.C
【详解】试题分析:根据圆周率的含义“圆的周长和它直径的比值,叫做圆周率”可知:圆周率是定值,不随圆的大小的变化而变化;进而解答即可。
解:根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率”可知:
半径3厘米的圆的圆周率等于半径5厘米的圆的圆周率;
故选C.
点评:此题考查了圆周率的含义。
8.C
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,用字母“π”表示它是一个无限不循环小数,进而解答。
【详解】根据圆周率的含义可知:圆周率π是一个无限不循环小数。
故答案为:C
【点睛】此题主要考查了学生对圆周率含义的理解。
9.3.44
10.16.56
【分析】拼成的长方形的两个长是圆的周长,宽是圆的半径,据此求出长方形的周长。
【详解】2×3.14×2+2×2
=12.56+4
=16.56(厘米)
【点睛】解答此题的关键是明白:拼成的长方形的两个长是圆的周长,宽是圆的半径。
11.直径,π,无限不循环,3.14。
【详解】试题分析:根据圆周率的含义:圆的周长和它直径的比值叫做圆周率,用字母“π”表示,π是一个无限不循环小数,计算时一般取它的近似值3.14;据此解答。
解:圆周率是圆的周长与 直径的比值,用字母 π来表示;它是一个 无限不循环小数,实际应用中一般取它的近似值,即 3.14。
故答案为直径,π,无限不循环,3.14。
点评:明确圆周率的含义是解答此题的关键。
12. ;半径
【分析】根据圆的面积推导公式,长方形的长相当于圆周长的一半,宽是圆的半径。
【详解】把一个圆平均分成若干份,可以拼成一个近似的长方形,长方形的长相当于圆周长的,宽相当于圆的半径。
【点睛】掌握圆面积的推导公式是解题关键,可以通过实际操作加深印象。
13.392.5
【分析】根据圆环面积公式:,即可代数解答。
【详解】3.14×(15-10)
=3.14×125
=392.5(平方厘米)
【点睛】此题主要考查了学生对圆环面积公式的实际解题能力,掌握公式是解题的关键。
14.O,OA,BC,3,3,6
【详解】试题分析:根据圆心、半径和直径的含义及同一圆中半径和直径之间的关系:把圆中心的一点叫做圆心,圆心用字母O表示,连接圆心和圆上任意一点的线段叫做半径;通过圆心并且两端都在圆上的线段叫做直径;同圆中直径是半径的2倍,据此解答即可。
解:由分析可知:点O是圆心,线段OA是半径,线段BC是直径,如果已知OA=3cm,那么OC=3cm,OB="3" cm,BC=6cm;
故答案为O,OA,BC,3,3,6。
点评:此题应根据圆心、半径和直径的含义及同一圆中半径和直径之间的关系进行解答。
15.√
【分析】通过圆心并且两端都在圆上的线段叫做直径,所以把圆形纸对折后形成的抓痕就是圆形纸的直径,据此即可解答。
【详解】根据直径的定义可知圆心一定在直径上,而两条折痕都是圆的直径,并且两条折痕只一个交点,说明这个交点就是圆心。
故答案为:正确。
【点睛】本题考查学生对圆、圆心、直径的认识。
16.正确
17.√
【分析】由图可知,长方形的长是宽的2倍,半圆的半径是长方形的宽,可求半圆的半径为24÷(2×2+1×2)=4厘米,再根据圆的面积公式求出半圆面积即可。
【详解】半圆半径:
24÷(2×2+1×2)
=24÷6
=4(厘米)
半圆面积:
=3.14×8
=25.12(平方厘米)
故答案为:√
【点睛】本题考查长方形周长和圆的面积,关键是从图中得知长方形的宽就是半圆的半径,长是半圆的直径。
18.×
【分析】圆的周长=2×π×半径,半径增加0.5米,周长增加(0.5×2×π)米。
【详解】半径增加0.5米,那么这个轮子滚一周的长度就增加:0.5×2×π=π(米),与题干不符。
故答案为:×
【点睛】此题考查半径改变,对周长的影响,需熟练掌握圆的周长公式。
19.√
【分析】圆的直径d=2r,据此解答。
【详解】一个圆的半径增加3厘米,直径增加2×3=6(厘米),原题说法正确。
故答案为:√
20.×
【分析】观察图形可知,左图涂色部分的周长等于直径是3厘米的圆的周长+3厘米×2,右侧图形涂色部分的周长等于直径是3厘米的圆的周长,所以左图涂色部分的周长大于右侧涂色部分的周长;左图涂色部分的面积等于边长是3厘米的正方形的面积减去直径是3厘米的圆的面积,右图涂色部分的面积等于边长是3厘米的正方形的面积减去直径是3厘米的圆的面积。所以左图涂色部分面积等于右图涂色部分面积。据此判断。
【详解】由分析可知,涂色部分的周长不相等,面积相等,原题说法错误。
故答案为:×
【点睛】此题考查了有关圆的阴影部分周长和面积的计算,认真观察图形解答即可。
21.√
【分析】假定圆的半径是1,面积是;半径扩大到原来的3倍后是3,面积是,据此解答。
【详解】假定圆的半径是1,根据题意则:
=9π÷π
=9
故原题说法正确。
【点睛】假定一个利用计算的数字做为圆的半径,正确运用圆的面积公式是解答本题的关键。
22.;21.98;1;0.24;230;
;;;;2
23.x=10;x=6;x=
24.71.4厘米
【详解】3.14×10+10×4=71.4(厘米)
25.28.26平方厘米
【详解】6÷2=3(厘米)
3.14×6×6÷2﹣3.14×3×3
=56.52﹣28.26
=28.26(平方厘米)
答:阴影部分的面积是28.26平方厘米.
26.113.04平方米
【详解】3.14×(8+2)2-3.14×82=113.04(平方米)
答:这条小路的占地面积是113.04平方米。
27.37.68 dm2
【分析】大圆的半径是4dm,小圆的半径是2dm,然后根据圆环的面积公式S=π(R2-r2);列式计算即可求解。
【详解】3.14×(42-22)
=3.14×12
=37.68(dm2)
答:阴影部分的面积是37.68dm2。
【点睛】本题考查了圆环的面积公式S=π(R2-r2)的灵活运用。
28.两只蚂蚁同时到达B点
【详解】首先根据图示,可得大圆的半径等于两个小圆的半径的和;然后根据圆的周长=2πr(r是圆的半径),可得大圆的周长的一半与两个小圆的周长的一半相等,所以两只蚂蚁走的路程相等,同时到达B点。
29.(1)39.6米(2)18.84米(3)30.144米
【详解】(1)36+(4-1)×1.2
=36+3.6
=39.6(米)
答:第4道的弯道半长是39.6米。
(2)(6-1)×1.2π
=5×12π
≈18.84(米)
答:第6道的运动员要比第1道的运动员提前约18.84米。
(3)(7-3)×1.2×2π
=4×1.2×2π
≈30.14(米)
答:第7道的运动员要比第3道运动员起跑点提前约30.14米。
30.314棵
【分析】根据圆的周长公式:周长=π×2×半径,代入数据,求出半径是15米的圆形池塘的周长;沿着它的边线每隔0.3米种一颗月季花,由于圆是封闭图形,相当于植树问题中的一端植树,一端不植树,即间距数=棵数,由此可知用圆的周长除以0.3,即可求出种多少棵月季花。
【详解】3.14×2×15÷0.3
=6.28×15÷0.3
=94.2÷0.3
=314(棵)
答:一共要种314棵月季花。
【点睛】利用圆的周长公式以及植树问题进行解答。
31.如图
【详解】试题分析:根据直径所对的圆周角是直角画图即可。
解:
(1)选择合适的直角三角板,用等腰直角三角板;
(2)用直角三角板的直角和圆上一点重合,沿两直角边划直线,连接两条直线与圆的交点,两圆之间的线段即为⊙O的直径;
(3)因为直角三角板上角的度数是一定的,所以过直角三角形的顶点向斜边作垂线即可。
斜边与垂线的交点即为该圆的圆心。
点评:本题是圆周角定理在实际生活中的运用,锻炼了学生对所学知识的应用能力。
32.9.14厘米;2.43平方厘米
【分析】由图可知:横截面的周长=3条正方形边长+直径是2厘米的圆的周长的一半;横截面的面积=边长是2厘米的正方形的面积-直径是2厘米的半圆的面积;代入数据计算即可。
【详解】横截面的周长:2×3+3.14×2÷2
=6+3.14
=9.14(厘米)
横截面的面积:2×2-3.14×(2÷2)2÷2
=4-3.14÷2
=2.43(平方厘米)
答:这个零件横截面(阴影部分)的周长9.14厘米,面积是2.43平方厘米。
【点睛】本题主要考查阴影部分的周长和面积,灵活运用圆的周长、面积公式计算即可。
第六单元《圆》
姓名:_________ 班级:_________ 学号:_________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.答题完成后,请再检查一下哦!
一、选择题
1.一个圆的直径是10cm,如果它的直径扩大为原来的2倍,则扩大后的圆的半径为( )
A.10cm B.5cm C.20cm D.15cm
2.任何圆的周长总是等于它的直径的( )。
A.3倍 B.3.14倍 C.3.1415926倍 D.π倍
3.在一个边长为2厘米的正方形内,画一个最大的圆,这个圆的直径是( )厘米.
A.1 B.2 C.4
4.从12时起,经过( )小时,时针经过的扇形圆心角是150°。
A.4 B.10 C.5 D.3
5.用一张长是7分米,宽2分米的长方形剪出一个最大的圆,像这样的圆最多可以剪( )个。
A.1 B.2 C.3 D.4
6.一个半圆的直径是6厘米,那么这个半圆的周长是( )厘米。
A.3π B.3π+6 C.6π D.6π+6
7.半径3厘米的圆的圆周率( )半径5厘米的圆的圆周率.
A.大于 B.小于 C.等于
8.圆周率π是一个( )。
A.有限小数 B.无限循环小数
C.无限不循环小数 D.以上都不对
二、填空题
9.如图,长方形的宽是4cm,图中阴影部分面积是________cm2
10.如图,将一个半径2厘米的圆形纸片平均分成若干份,剪开后拼成一个近似的长方形,拼成的近似长方形的周长是__________厘米。
11.圆周率是圆的周长与__________的比值,用字母__________来表示;它是一个__________小数,实际应用中一般取它的近似值,即__________。
12.把一个圆平均分成若干份,可以拼成一个近似的长方形,长方形的长相当于圆周长的,宽相当于圆的__________。
13.图中阴影部分的面积__________平方厘米。(单位:厘米)(π取3.14)
14.如图,点__________是圆心,线段__________是半径,线段__________是直径,如果已知OA=3cm,,那么OC=__________cm.,OB=__________cm,BC=__________cm.
三、判断题
15.把一张圆形纸片对折后打开,换个方向再对折.两条折痕的交点就是这个圆的圆心.( )
16.当圆的直径和正方形的边长相等时,正方形的面积比圆的面积大.( )
17.下图中长方形周长是24厘米,半圆面积就是25.12平方厘米。( )
18.一个圆形轮子的半径增加0.5米,那么这个轮子滚一周的长度就增加1米。( )
19.一个圆的半径增加3厘米,直径就会增加6厘米。( )
20.下图两个正方形的边长都是3厘米,涂色部分的周长和面积分别相等。( )
21.圆的半径扩大到原来的3倍,面积就扩大到原来的9倍。( )
四、计算题
22.直接写出得数。
7÷9= 7π≈ 0.17+0.83= 0.52-0.28= 2.3÷0.01=
23.解方程.
五、图形计算
24.求下图中阴影部分的周长。(单位:厘米)
25.求阴影部分的面积.(单位:厘米)
六、解答题
26.一个半径8米的圆形小花坛,周围有一条2米宽的小路(如下图)。求这条小路的占地面积。
27.如图,大圆的半径是4dm,小圆的半径是2dm,图中阴影部分的面积是多少dm2?(π取3.14)
28.有两只蚂蚁同时从A点到B点,一只走路线①,另一只走路线②,它们的速度相同,问它们谁先到达B点(如图).
29.如果标准的400米跑道的弯道是半圆形,且最内圈的半径为36米,每条跑道宽为1.2米,现有8条跑道(π≈3.14)
(1)第4道的弯道半长是多少米?
(2)若进行200米赛跑,第6道的运动员要比第1道的运动员提前约多少米?(保留两位小数)
(3)若进行400米赛跑,第7道的运动员要比第3道运动员起跑点提前约多少米?(保留两位小数)
30.一个圆形池塘的半径是15米,沿着它的边线大约每隔0.3米种一棵月季花,一共要种多少棵月季花?
31.你能用直角三角板或直尺找出 一个圆的圆心吗?简要地写出你的解决问题的想法或在图中画出你的思路.(一种方法的5分)
32.如图,是一种零件横截面的示意图,这个零件横截面(阴影部分)的周长和面积各是多少?
参考答案
1.A
【详解】试题分析:根据同圆中半径和直径的关系可知“r=d÷2”,进行解答即可。
解:原来圆的直径是l0cm,如果它的直径扩大为原来的2倍,则变成了20cm,根据r=d÷2=20÷2=10(厘米);故选A.
点评:此题考查了同圆中半径和直径的关系。
2.D
【详解】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,即圆的周长是直径的π倍。
故答案为:D。
3.B
【详解】抓住“最大的圆就是直径等于正方形边长2厘米的圆”,即可解决问题。此题关键是根据正方形内最大的圆的特点得出:圆的直径等于正方形的边长。
4.C
【解析】根据题意,因为分针每转一个大格是30°,所以我们用总角度除以30°即可。
【详解】150÷30=5
故答案为:C
【点睛】此题考查学生需要知道在钟表内,分针每转一个大格是30°。
5.C
【详解】试题分析:在一张长是7分米,宽2分米的长方形里面剪最大的圆,应以长方形的宽边为圆的直径剪,看一看长7分米里面有几个2分米即可。
解:以长方形的宽边为圆的直径剪,
最多可以剪:7÷2=3(个)…1;
答:像这样的圆最多可以剪3个。故选C
点评:此题考查在长方形里剪圆的个数,应以宽边为直径剪,再看长边里有几个宽边的长度即可确定圆的个数。
6.B
【解析】半圆的周长是由半圆弧加直径组成,通过圆的周长公式:,求出圆的周长,再除以2,最后加上直径即可解答。
【详解】6×π÷2+6
=6π÷2+6
=3π+6(厘米)
故答案为:B
【点睛】此题关键在于理解半圆的周长是由半圆弧加直径组成。
7.C
【详解】试题分析:根据圆周率的含义“圆的周长和它直径的比值,叫做圆周率”可知:圆周率是定值,不随圆的大小的变化而变化;进而解答即可。
解:根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率”可知:
半径3厘米的圆的圆周率等于半径5厘米的圆的圆周率;
故选C.
点评:此题考查了圆周率的含义。
8.C
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,用字母“π”表示它是一个无限不循环小数,进而解答。
【详解】根据圆周率的含义可知:圆周率π是一个无限不循环小数。
故答案为:C
【点睛】此题主要考查了学生对圆周率含义的理解。
9.3.44
10.16.56
【分析】拼成的长方形的两个长是圆的周长,宽是圆的半径,据此求出长方形的周长。
【详解】2×3.14×2+2×2
=12.56+4
=16.56(厘米)
【点睛】解答此题的关键是明白:拼成的长方形的两个长是圆的周长,宽是圆的半径。
11.直径,π,无限不循环,3.14。
【详解】试题分析:根据圆周率的含义:圆的周长和它直径的比值叫做圆周率,用字母“π”表示,π是一个无限不循环小数,计算时一般取它的近似值3.14;据此解答。
解:圆周率是圆的周长与 直径的比值,用字母 π来表示;它是一个 无限不循环小数,实际应用中一般取它的近似值,即 3.14。
故答案为直径,π,无限不循环,3.14。
点评:明确圆周率的含义是解答此题的关键。
12. ;半径
【分析】根据圆的面积推导公式,长方形的长相当于圆周长的一半,宽是圆的半径。
【详解】把一个圆平均分成若干份,可以拼成一个近似的长方形,长方形的长相当于圆周长的,宽相当于圆的半径。
【点睛】掌握圆面积的推导公式是解题关键,可以通过实际操作加深印象。
13.392.5
【分析】根据圆环面积公式:,即可代数解答。
【详解】3.14×(15-10)
=3.14×125
=392.5(平方厘米)
【点睛】此题主要考查了学生对圆环面积公式的实际解题能力,掌握公式是解题的关键。
14.O,OA,BC,3,3,6
【详解】试题分析:根据圆心、半径和直径的含义及同一圆中半径和直径之间的关系:把圆中心的一点叫做圆心,圆心用字母O表示,连接圆心和圆上任意一点的线段叫做半径;通过圆心并且两端都在圆上的线段叫做直径;同圆中直径是半径的2倍,据此解答即可。
解:由分析可知:点O是圆心,线段OA是半径,线段BC是直径,如果已知OA=3cm,那么OC=3cm,OB="3" cm,BC=6cm;
故答案为O,OA,BC,3,3,6。
点评:此题应根据圆心、半径和直径的含义及同一圆中半径和直径之间的关系进行解答。
15.√
【分析】通过圆心并且两端都在圆上的线段叫做直径,所以把圆形纸对折后形成的抓痕就是圆形纸的直径,据此即可解答。
【详解】根据直径的定义可知圆心一定在直径上,而两条折痕都是圆的直径,并且两条折痕只一个交点,说明这个交点就是圆心。
故答案为:正确。
【点睛】本题考查学生对圆、圆心、直径的认识。
16.正确
17.√
【分析】由图可知,长方形的长是宽的2倍,半圆的半径是长方形的宽,可求半圆的半径为24÷(2×2+1×2)=4厘米,再根据圆的面积公式求出半圆面积即可。
【详解】半圆半径:
24÷(2×2+1×2)
=24÷6
=4(厘米)
半圆面积:
=3.14×8
=25.12(平方厘米)
故答案为:√
【点睛】本题考查长方形周长和圆的面积,关键是从图中得知长方形的宽就是半圆的半径,长是半圆的直径。
18.×
【分析】圆的周长=2×π×半径,半径增加0.5米,周长增加(0.5×2×π)米。
【详解】半径增加0.5米,那么这个轮子滚一周的长度就增加:0.5×2×π=π(米),与题干不符。
故答案为:×
【点睛】此题考查半径改变,对周长的影响,需熟练掌握圆的周长公式。
19.√
【分析】圆的直径d=2r,据此解答。
【详解】一个圆的半径增加3厘米,直径增加2×3=6(厘米),原题说法正确。
故答案为:√
20.×
【分析】观察图形可知,左图涂色部分的周长等于直径是3厘米的圆的周长+3厘米×2,右侧图形涂色部分的周长等于直径是3厘米的圆的周长,所以左图涂色部分的周长大于右侧涂色部分的周长;左图涂色部分的面积等于边长是3厘米的正方形的面积减去直径是3厘米的圆的面积,右图涂色部分的面积等于边长是3厘米的正方形的面积减去直径是3厘米的圆的面积。所以左图涂色部分面积等于右图涂色部分面积。据此判断。
【详解】由分析可知,涂色部分的周长不相等,面积相等,原题说法错误。
故答案为:×
【点睛】此题考查了有关圆的阴影部分周长和面积的计算,认真观察图形解答即可。
21.√
【分析】假定圆的半径是1,面积是;半径扩大到原来的3倍后是3,面积是,据此解答。
【详解】假定圆的半径是1,根据题意则:
=9π÷π
=9
故原题说法正确。
【点睛】假定一个利用计算的数字做为圆的半径,正确运用圆的面积公式是解答本题的关键。
22.;21.98;1;0.24;230;
;;;;2
23.x=10;x=6;x=
24.71.4厘米
【详解】3.14×10+10×4=71.4(厘米)
25.28.26平方厘米
【详解】6÷2=3(厘米)
3.14×6×6÷2﹣3.14×3×3
=56.52﹣28.26
=28.26(平方厘米)
答:阴影部分的面积是28.26平方厘米.
26.113.04平方米
【详解】3.14×(8+2)2-3.14×82=113.04(平方米)
答:这条小路的占地面积是113.04平方米。
27.37.68 dm2
【分析】大圆的半径是4dm,小圆的半径是2dm,然后根据圆环的面积公式S=π(R2-r2);列式计算即可求解。
【详解】3.14×(42-22)
=3.14×12
=37.68(dm2)
答:阴影部分的面积是37.68dm2。
【点睛】本题考查了圆环的面积公式S=π(R2-r2)的灵活运用。
28.两只蚂蚁同时到达B点
【详解】首先根据图示,可得大圆的半径等于两个小圆的半径的和;然后根据圆的周长=2πr(r是圆的半径),可得大圆的周长的一半与两个小圆的周长的一半相等,所以两只蚂蚁走的路程相等,同时到达B点。
29.(1)39.6米(2)18.84米(3)30.144米
【详解】(1)36+(4-1)×1.2
=36+3.6
=39.6(米)
答:第4道的弯道半长是39.6米。
(2)(6-1)×1.2π
=5×12π
≈18.84(米)
答:第6道的运动员要比第1道的运动员提前约18.84米。
(3)(7-3)×1.2×2π
=4×1.2×2π
≈30.14(米)
答:第7道的运动员要比第3道运动员起跑点提前约30.14米。
30.314棵
【分析】根据圆的周长公式:周长=π×2×半径,代入数据,求出半径是15米的圆形池塘的周长;沿着它的边线每隔0.3米种一颗月季花,由于圆是封闭图形,相当于植树问题中的一端植树,一端不植树,即间距数=棵数,由此可知用圆的周长除以0.3,即可求出种多少棵月季花。
【详解】3.14×2×15÷0.3
=6.28×15÷0.3
=94.2÷0.3
=314(棵)
答:一共要种314棵月季花。
【点睛】利用圆的周长公式以及植树问题进行解答。
31.如图
【详解】试题分析:根据直径所对的圆周角是直角画图即可。
解:
(1)选择合适的直角三角板,用等腰直角三角板;
(2)用直角三角板的直角和圆上一点重合,沿两直角边划直线,连接两条直线与圆的交点,两圆之间的线段即为⊙O的直径;
(3)因为直角三角板上角的度数是一定的,所以过直角三角形的顶点向斜边作垂线即可。
斜边与垂线的交点即为该圆的圆心。
点评:本题是圆周角定理在实际生活中的运用,锻炼了学生对所学知识的应用能力。
32.9.14厘米;2.43平方厘米
【分析】由图可知:横截面的周长=3条正方形边长+直径是2厘米的圆的周长的一半;横截面的面积=边长是2厘米的正方形的面积-直径是2厘米的半圆的面积;代入数据计算即可。
【详解】横截面的周长:2×3+3.14×2÷2
=6+3.14
=9.14(厘米)
横截面的面积:2×2-3.14×(2÷2)2÷2
=4-3.14÷2
=2.43(平方厘米)
答:这个零件横截面(阴影部分)的周长9.14厘米,面积是2.43平方厘米。
【点睛】本题主要考查阴影部分的周长和面积,灵活运用圆的周长、面积公式计算即可。
