山东省聊城市第四中学人教版高中数学必修五学案:2.1 数列的概念与简单表示方法(2)(无答案)
文档属性
| 名称 | 山东省聊城市第四中学人教版高中数学必修五学案:2.1 数列的概念与简单表示方法(2)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 31.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-12 00:00:00 | ||
图片预览

文档简介
数列的概念与简单表示方法(2)
一、学习目标
1.探索并掌握数列的几种简单表示方法.
2.了解数列的递推公式,并会利用递推公式求数列的前若干项.
3.会用通项公式表示一些数列并能应用它解决一些简单的问题
二、课前知多少:
1.函数的表示方法: .
2.什么是数列的通项公式?________________________________________________.
三、合作探究 问题解决
函数的表示法 数列的表示法
问题1:如何表示一个数列?
问题2:你能分别举例说明吗?
数列的表示法 例子
问题3:谈一谈你对数列表示方法的认识.
例题1.下图中的三角形称为谢宾斯基三角形 ( http: / / www.21cnjy.com ).在下图四个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在坐标系中画出它的图象
例题2.已知数列满足,,写出该数列的前5项以及它的通项公式.
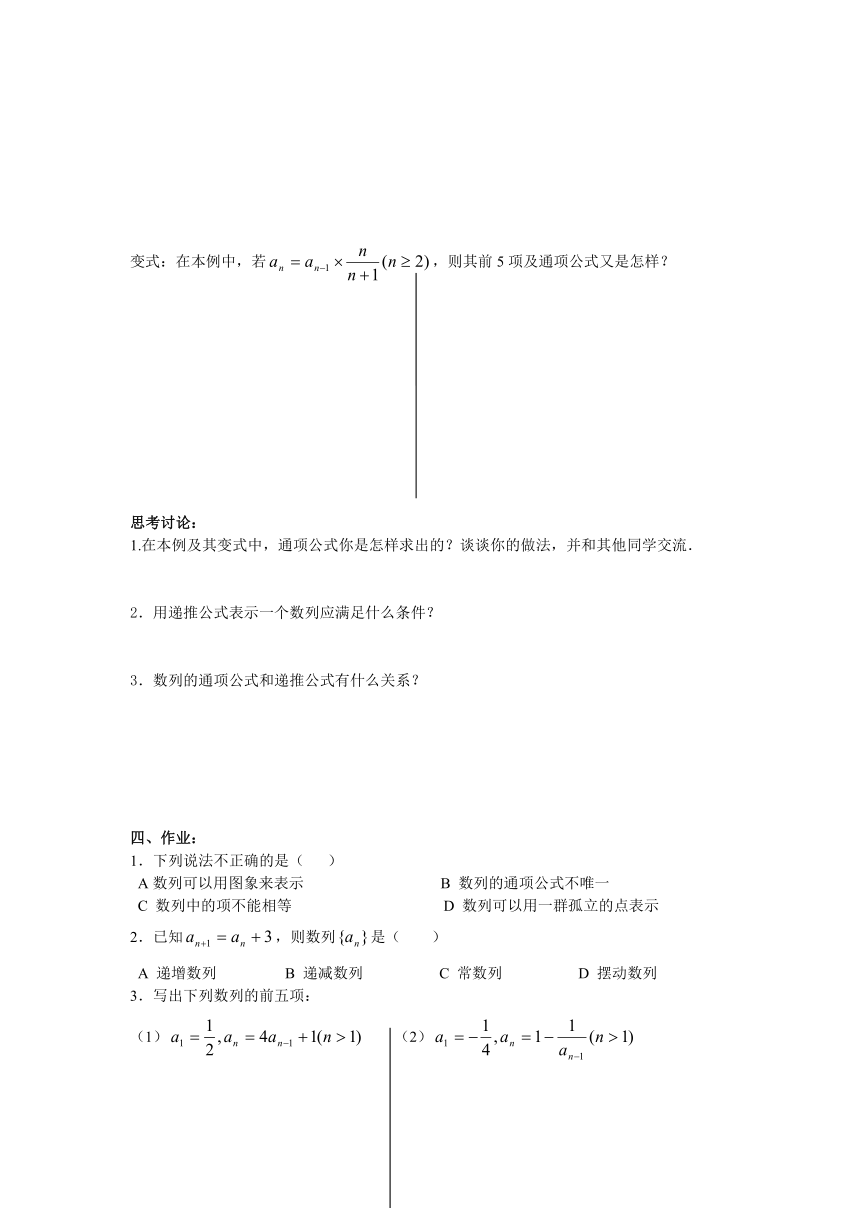
变式:在本例中,若,则其前5项及通项公式又是怎样?
思考讨论:
1.在本例及其变式中,通项公式你是怎样求出的?谈谈你的做法,并和其他同学交流.
2.用递推公式表示一个数列应满足什么条件?
3.数列的通项公式和递推公式有什么关系?
四、作业:
1.下列说法不正确的是( )
A数列可以用图象来表示 B 数列的通项公式不唯一
C 数列中的项不能相等 D 数列可以用一群孤立的点表示
2.已知,则数列是( )
A 递增数列 B 递减数列 C 常数列 D 摆动数列
3.写出下列数列的前五项:
(1) (2)
思考:在(2)中,______
4.分别写出三角形数(见教材第28页)构成的数列的第5项,第6项和第7项,并写出它的一个递推公式.
5.(1)在数列中,,则是此数列的第_____项.
(2)数列的通项公式,则是此数列的第_____项.
6.根据下面4个数列的通项公式,分别作出它们的图象:
(1); (2);
(3); (4)
7.已知数列的第一项是1,第二项是2,以后各项由给出.
(1)写出这个数列的前5项;
(2)利用上面的数列,通过公式构造一个新的数列,试写出数列的前5项
8.在数列中,,通项公式是项数n的一次函数.
求数列的通项公式;
88是否是数列中的项
x 1 2 3 4 5
f(x) 5 1 3 4 2
9.(选做)函数定义如右表,数列满足,且对任意的自然数均有.则( )
A 1 B 2 C 4 D 5
一、学习目标
1.探索并掌握数列的几种简单表示方法.
2.了解数列的递推公式,并会利用递推公式求数列的前若干项.
3.会用通项公式表示一些数列并能应用它解决一些简单的问题
二、课前知多少:
1.函数的表示方法: .
2.什么是数列的通项公式?________________________________________________.
三、合作探究 问题解决
函数的表示法 数列的表示法
问题1:如何表示一个数列?
问题2:你能分别举例说明吗?
数列的表示法 例子
问题3:谈一谈你对数列表示方法的认识.
例题1.下图中的三角形称为谢宾斯基三角形 ( http: / / www.21cnjy.com ).在下图四个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在坐标系中画出它的图象
例题2.已知数列满足,,写出该数列的前5项以及它的通项公式.
变式:在本例中,若,则其前5项及通项公式又是怎样?
思考讨论:
1.在本例及其变式中,通项公式你是怎样求出的?谈谈你的做法,并和其他同学交流.
2.用递推公式表示一个数列应满足什么条件?
3.数列的通项公式和递推公式有什么关系?
四、作业:
1.下列说法不正确的是( )
A数列可以用图象来表示 B 数列的通项公式不唯一
C 数列中的项不能相等 D 数列可以用一群孤立的点表示
2.已知,则数列是( )
A 递增数列 B 递减数列 C 常数列 D 摆动数列
3.写出下列数列的前五项:
(1) (2)
思考:在(2)中,______
4.分别写出三角形数(见教材第28页)构成的数列的第5项,第6项和第7项,并写出它的一个递推公式.
5.(1)在数列中,,则是此数列的第_____项.
(2)数列的通项公式,则是此数列的第_____项.
6.根据下面4个数列的通项公式,分别作出它们的图象:
(1); (2);
(3); (4)
7.已知数列的第一项是1,第二项是2,以后各项由给出.
(1)写出这个数列的前5项;
(2)利用上面的数列,通过公式构造一个新的数列,试写出数列的前5项
8.在数列中,,通项公式是项数n的一次函数.
求数列的通项公式;
88是否是数列中的项
x 1 2 3 4 5
f(x) 5 1 3 4 2
9.(选做)函数定义如右表,数列满足,且对任意的自然数均有.则( )
A 1 B 2 C 4 D 5
