第五单元 三角形(单元练习)2023-2024学年四年级下册数学人教版(含答案)
文档属性
| 名称 | 第五单元 三角形(单元练习)2023-2024学年四年级下册数学人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 111.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览

文档简介
第五单元 三角形(单元练习)2023-2024学年四年级下册数学人教版
一、单选题
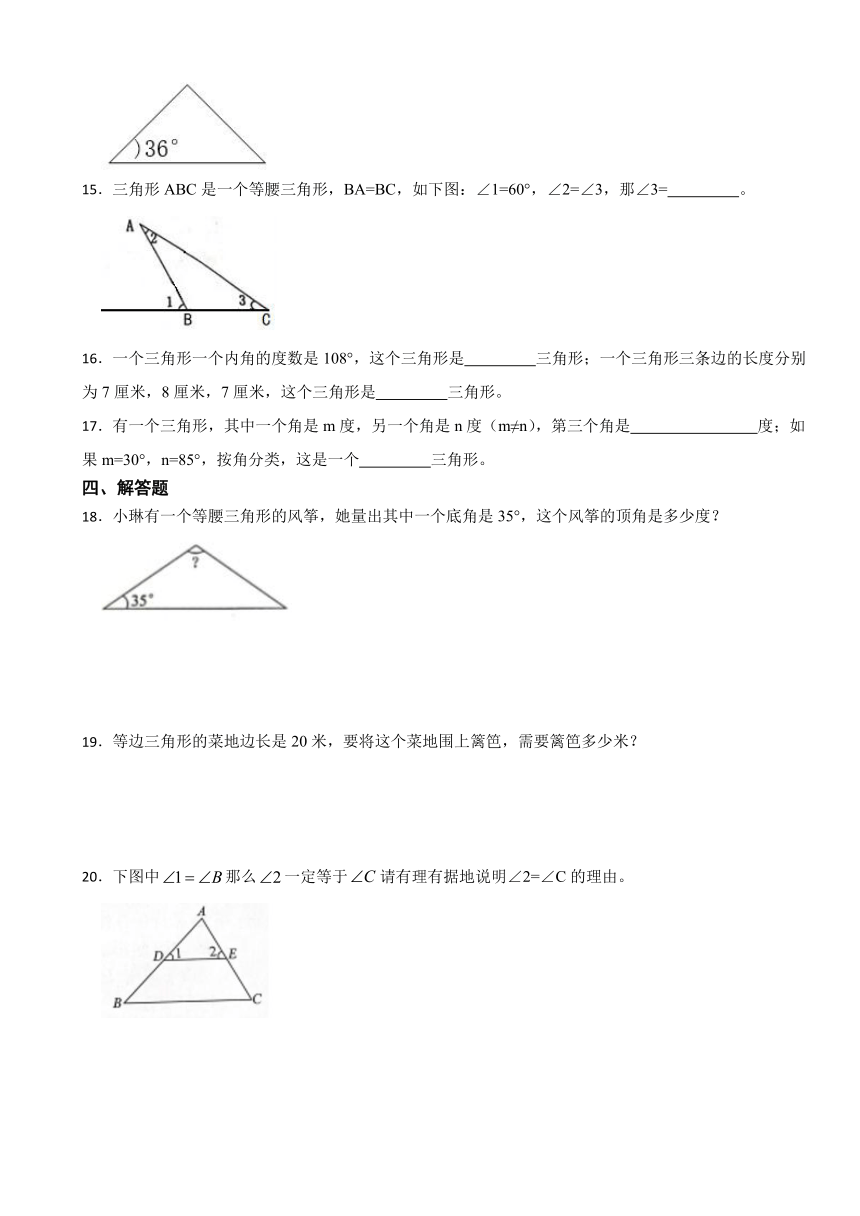
1.把直线外一点与直线上任意一点连接起来,可以画很多条( )。
A.射线 B.直线 C.线段
2.下面被遮住的三角形中,( )一定是钝角三角形。
A. B. C.
3.等腰三角形中有一个底角是55度,顶角是( )度。
A.55 B.125 C.70
4.一个三角形的两条边分别是3cm和4cm,这个三角形一定不是( )三角形。
A.锐角 B.等腰 C.等边
5.一个钝角三角形,已知它的两条边的长度都是6cm,那么这个三角形第三条边的长度可能是( )
A.6 cm B.10 cm C.14 cm
二、判断题
6.用5cm,9cm,4cm长的三根小棒,可以拼成一个三角形。( )
7.一个等腰三角形的一个腰和底边的长度可以是5cm和8cm。( )
8.如果直角三角形的一个锐角是45°,这个三角形一定是等腰三角形。( )
9.三角形都有三条高,两个锐角。 ( )
10.用3根分别长6厘米、7厘米、8厘米的小棒一定能围成三角形.( )
三、填空题
11.房屋的屋架做成三角形是应用了三角形的 ,还有 也是运用这一特性设计的。
12.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 。
13.等边三角形的三条边长度 ,每个内角都是 度。
14.如图,一个等腰三角形有一个底角度数是36°,另外两个内角度数是 和 ,这还是一个 三角形。
15.三角形ABC是一个等腰三角形,BA=BC,如下图:∠1=60°,∠2=∠3,那∠3= 。
16.一个三角形一个内角的度数是108°,这个三角形是 三角形;一个三角形三条边的长度分别为7厘米,8厘米,7厘米,这个三角形是 三角形。
17.有一个三角形,其中一个角是m度,另一个角是n度(m≠n),第三个角是 度;如果m=30°,n=85°,按角分类,这是一个 三角形。
四、解答题
18.小琳有一个等腰三角形的风筝,她量出其中一个底角是35°,这个风筝的顶角是多少度?
19.等边三角形的菜地边长是20米,要将这个菜地围上篱笆,需要篱笆多少米?
20.下图中那么一定等于请有理有据地说明∠2=∠C的理由。
21.三角形ABC是一个直角三角形,三角形BDC是一个等腰三角形,∠1=∠2,∠3=42°,求∠4的度数。
22.一个等腰三角形的周长是23厘米,它的底边比一条腰长的2倍少1厘米,这个三角形的底边长多少厘米?
23.把一根15cm长的吸管剪成3段(每段都是整厘米数),怎样剪才能围成一个三角形?共有几种不同的剪法?请说明理由并全部列举出来。
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】错误
7.【答案】正确
8.【答案】正确
9.【答案】正确
10.【答案】正确
11.【答案】稳定性;照相机的支架
12.【答案】三角形具有稳定性
13.【答案】相等;60
14.【答案】36°;108°;钝角
15.【答案】30°
16.【答案】钝角;等腰
17.【答案】(180-m-n);锐角
18.【答案】解:180°-(35°+35°)
=180°-70°
=110°
答:这个风筝的顶角是110度。
19.【答案】解:20×3=60(米)
答:需要篱笆60米。
20.【答案】解:在三角形ADE中,∠2=180度-∠A-∠1.
在三角形ABC中,∠C=180度-∠A-∠B.
因为∠1=∠B,所以∠2=∠C。
21.【答案】解:90°-42°=48°
180°-48°×2
=180°-96°
=84°
答:∠4的度数是84°。
22.【答案】解:23+1=24(厘米)
24÷(1+1+2)=6(厘米)
23-6×2=11(厘米)
答:这个三角形的底边长11厘米。
23.【答案】解:①1cm、7cm、7cm;
②2cm、6cm、7cm;
③3cm、5cm、7cm;
④3cm、6cm、6cm;
⑤4cm、4cm、7cm;
⑥4cm、5cm、6cm;
⑦5cm、5cm、5cm;
答:共有7种不同的剪法。因为三角形任意两边之和大于第三边。
一、单选题
1.把直线外一点与直线上任意一点连接起来,可以画很多条( )。
A.射线 B.直线 C.线段
2.下面被遮住的三角形中,( )一定是钝角三角形。
A. B. C.
3.等腰三角形中有一个底角是55度,顶角是( )度。
A.55 B.125 C.70
4.一个三角形的两条边分别是3cm和4cm,这个三角形一定不是( )三角形。
A.锐角 B.等腰 C.等边
5.一个钝角三角形,已知它的两条边的长度都是6cm,那么这个三角形第三条边的长度可能是( )
A.6 cm B.10 cm C.14 cm
二、判断题
6.用5cm,9cm,4cm长的三根小棒,可以拼成一个三角形。( )
7.一个等腰三角形的一个腰和底边的长度可以是5cm和8cm。( )
8.如果直角三角形的一个锐角是45°,这个三角形一定是等腰三角形。( )
9.三角形都有三条高,两个锐角。 ( )
10.用3根分别长6厘米、7厘米、8厘米的小棒一定能围成三角形.( )
三、填空题
11.房屋的屋架做成三角形是应用了三角形的 ,还有 也是运用这一特性设计的。
12.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 。
13.等边三角形的三条边长度 ,每个内角都是 度。
14.如图,一个等腰三角形有一个底角度数是36°,另外两个内角度数是 和 ,这还是一个 三角形。
15.三角形ABC是一个等腰三角形,BA=BC,如下图:∠1=60°,∠2=∠3,那∠3= 。
16.一个三角形一个内角的度数是108°,这个三角形是 三角形;一个三角形三条边的长度分别为7厘米,8厘米,7厘米,这个三角形是 三角形。
17.有一个三角形,其中一个角是m度,另一个角是n度(m≠n),第三个角是 度;如果m=30°,n=85°,按角分类,这是一个 三角形。
四、解答题
18.小琳有一个等腰三角形的风筝,她量出其中一个底角是35°,这个风筝的顶角是多少度?
19.等边三角形的菜地边长是20米,要将这个菜地围上篱笆,需要篱笆多少米?
20.下图中那么一定等于请有理有据地说明∠2=∠C的理由。
21.三角形ABC是一个直角三角形,三角形BDC是一个等腰三角形,∠1=∠2,∠3=42°,求∠4的度数。
22.一个等腰三角形的周长是23厘米,它的底边比一条腰长的2倍少1厘米,这个三角形的底边长多少厘米?
23.把一根15cm长的吸管剪成3段(每段都是整厘米数),怎样剪才能围成一个三角形?共有几种不同的剪法?请说明理由并全部列举出来。
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】错误
7.【答案】正确
8.【答案】正确
9.【答案】正确
10.【答案】正确
11.【答案】稳定性;照相机的支架
12.【答案】三角形具有稳定性
13.【答案】相等;60
14.【答案】36°;108°;钝角
15.【答案】30°
16.【答案】钝角;等腰
17.【答案】(180-m-n);锐角
18.【答案】解:180°-(35°+35°)
=180°-70°
=110°
答:这个风筝的顶角是110度。
19.【答案】解:20×3=60(米)
答:需要篱笆60米。
20.【答案】解:在三角形ADE中,∠2=180度-∠A-∠1.
在三角形ABC中,∠C=180度-∠A-∠B.
因为∠1=∠B,所以∠2=∠C。
21.【答案】解:90°-42°=48°
180°-48°×2
=180°-96°
=84°
答:∠4的度数是84°。
22.【答案】解:23+1=24(厘米)
24÷(1+1+2)=6(厘米)
23-6×2=11(厘米)
答:这个三角形的底边长11厘米。
23.【答案】解:①1cm、7cm、7cm;
②2cm、6cm、7cm;
③3cm、5cm、7cm;
④3cm、6cm、6cm;
⑤4cm、4cm、7cm;
⑥4cm、5cm、6cm;
⑦5cm、5cm、5cm;
答:共有7种不同的剪法。因为三角形任意两边之和大于第三边。
