2.长方体和正方体的表面积 (课件)-五年级下册数学人教版(共55张PPT)
文档属性
| 名称 | 2.长方体和正方体的表面积 (课件)-五年级下册数学人教版(共55张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 20:00:11 | ||
图片预览







文档简介
(共55张PPT)
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
第1课时 长方体、正方体的展开图
1.通过动手操作,知道长方体、正方体的不同的展开图,加深对正方体、长方体特点的认识。
2.经历展开与折叠的活动过程,在想象、操作等活动中,初步感知平面图形与立体图形的关系,发展空间观念。
3.激发学习数学的兴趣,渗透转化思想。
学习目标
【重点】
经历纸盒展开的过程,能在自己的展开图上找到对应的面。
【难点】
能指出其他展开图中相对的面,根据展开图判断能否围成长方体或正方体。
投票箱
晨光小学要举行大队委选举,需要制作一个投票箱(如图)。
应该如何制作呢?
课堂导入
新知探究
把一个长方体或正方体的纸盒展开是什么形状的呢?
要沿着棱剪开。
我展开了一个长方体的纸盒。
正方体的纸盒可以这样展开。
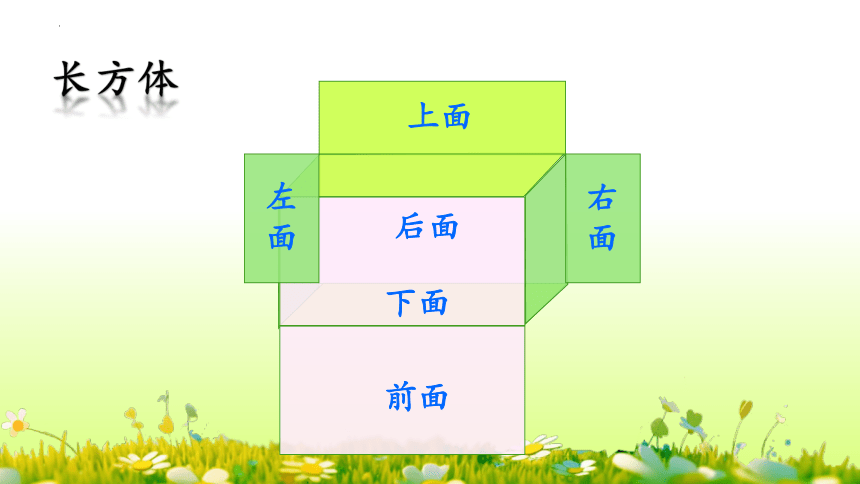
长方体
上面
前面
右面
左面
后面
下面
上面
前面
后面
下面
右面
左面
左面
长方体
上
前
右
左
后
下
观察长方体展开图,回答下面的问题。
(1)哪些面的面积相等?
前面=后面
上面=下面
左面=右面
上
后
右
前
下
a
b
h
a
a
b
b
左
b
h
b
h
a
h
a
h
上
下
左
右
前
后
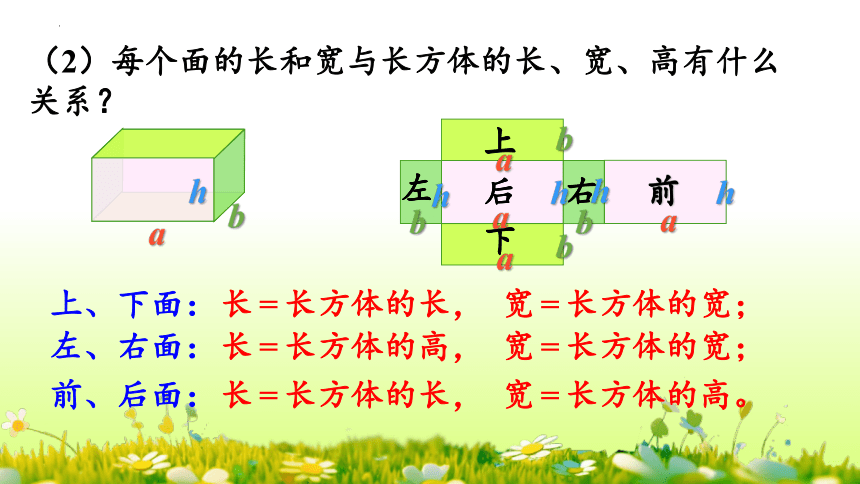
上、下面:长=长方体的长, 宽=长方体的宽;
左、右面:长=长方体的高, 宽=长方体的宽;
前、后面:长=长方体的长, 宽=长方体的高。
(2)每个面的长和宽与长方体的长、宽、高有什么关系?
上
前
右
左
后
下
上
左
后
右
前
下
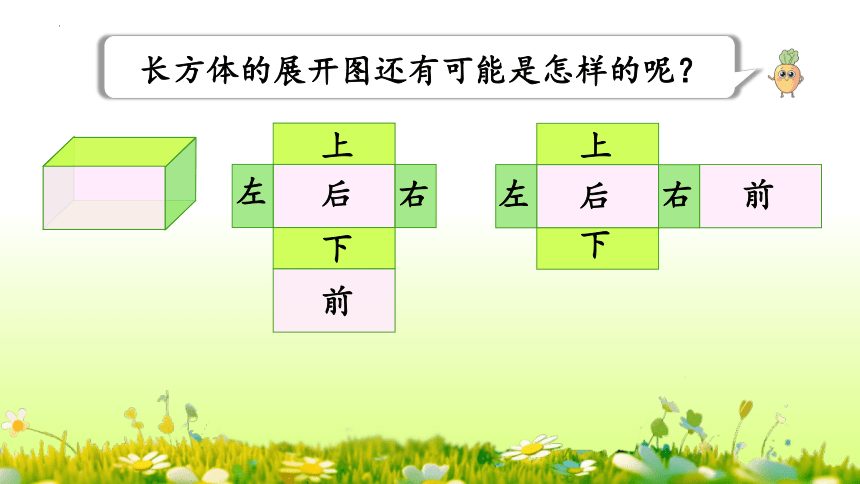
长方体的展开图还有可能是怎样的呢?
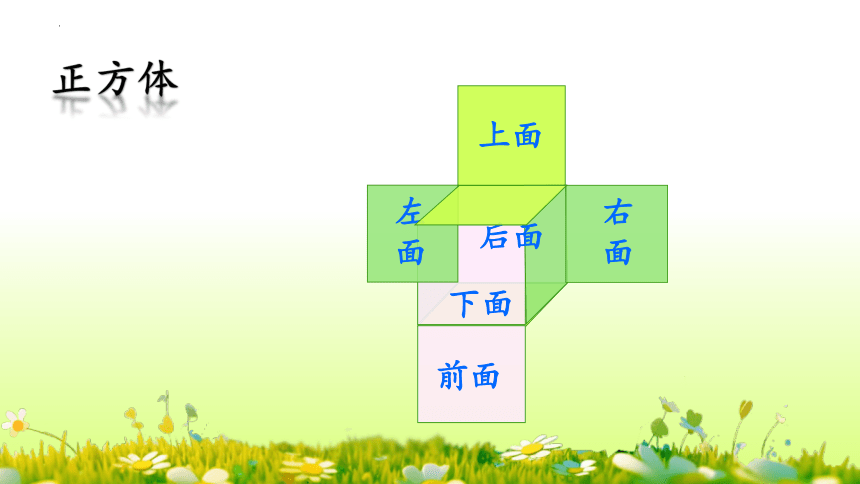
正方体
上面
前面
右面
左面
后面
下面
上面
前面
右面
左面
后面
下面
正方体
正方体的展开图还有可能是怎样的呢?
“141”型
“231”型
“222”型
“33”型
注意:任何正方体的展开图不能是“田字型”,
也不能是“凹字型”。
1.下列哪些图形是长方体的展开图?在括号内画“√”。
( )
( )
( )
课堂练习
2.下列哪些图形是正方体的展开图?在括号内画“√”。
( )
( )
( )
( )
正方体的展开图不能是“凹字型”,也不能是“田字型”。
3.下面是一幅不完整的正方体展开图。
①
②
③
④
⑤
⑥
(1) 可能在图中的哪个位置。
(2)图中①的对面是( ) ,
②的对面是( )。
⑥
⑤
④
⑥
⑥
(3)如果前面是②,右面是③,
那么上面是( ),下面是( )。
①
⑤
4.把下面这个展开图折成一个长方体。
(1)如果字母A在底部,那么字母( )在上面。
拓展提升
A
B
C
D
F
E
E
4.把下面这个展开图折成一个长方体。
A
B
C
D
F
E
(2)如果字母F在前面,从左边看是字母B,那么字母( )在上面。
E
课堂小结
展开图
1.长方体和正方体展开图的形状不是唯一的,展开的方法不同,得到的展开图不相同。但不管怎样展开,相对的两个面不可能相邻。
2.借助长方体和正方体的展开图可以探究各个面之间的关系。
这节课你有哪些收获?
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
第2课时 长方体、正方体表面积的计算
1.理解长方体和正方体的表面积意义,初步学会计算长方体和正方体表面积的方法。
2.能根据现实情景和信息,通过动手操作、小组合作、观察思考等解决问题的方法,去探求、经历、感受长方体和正方体的表面积概念和计算方法,初步培养探究意识和提升探求能力。
3. 感受到数学与生活的密切联系,培养初步的数学应用意识,并在探究过程中获得积极的数学情感体验。
学习目标
【重难点】
理解表面积的意义,探索长方体和正方体表面积的计算方法,能根据实际情况计算物体的表面积。
长方体或正方体6个面的总面积,叫作它的表面积。
日常生活和生产中,经常需要计算一些长方体或正方体的表面积。
课堂导入
制作尺寸如下图所示的长方体和正方体保温箱,各需要多少平方分米的泡沫板?(单位:dm)
这里要求的是这个长方体和正方体的 。
表面积
新知探究
长方体和正方体6个面的面积之和,叫作它的表面积。
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
新知探究
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
S表
6×5
=148(dm )
6×4
4×5
+
=30+30+24+24+20+20
S上
=
+
S下
S前
S后
S左
S右
+
+
+
+
6×5
6×4
4×5
+
+
+
+
=6×5×2+6×4×2+5×4×2
新知探究
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
=60+48+40
=148(dm2)
新知探究
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
=(6×5+6×4+5×4)×2
=74×2
=148(dm2)
答:需要148平方分米的泡沫板。
长方体的表面积
S表=2ab+2ah+2bh
宽(b)
长(a)
高(h)
S表=(ab+ah+bh)×2
公式推导
=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
新知探究
正方体表面积=棱长×棱长×6
S表=6a
棱长(a)
棱长(a)
棱长(a)
新知探究
棱长(a)
棱长(a)
棱长(a)
=5×5×6
=25×6
=150 (dm2)
答:需要150平方分米的泡沫板。
课堂练习
0.75m
0.5m
1.6m
0.75×1.6×2+0.5×1.6×2+0.75×0.5
=2.4+1.6+0.375
=4.375(m )
答:至少需要4.375 m 的布料。
教材第24页做一做
1. 一个长0.75 m、宽0.5 m、高1.6 m的简易衣柜需要换布罩(如图,没有底面)。至少需要多少平方米布料?
没有底面,这个布罩就只有5个面,要求的就是前后左右面和上面这5个面的面积和。
2. 计算下面长方体的表面积。(单位:dm)
(12×5+12×5+5×5)×2
=145×2
=290(dm )
12×5×4+5×5×2
=240+50
=290(dm )
方法1:
方法2:
12
5
5
答:长方体的表面积是290 dm 。
拓展提升
3. 下面是一个长方体的展开图,求长方体的表面积。(单位:dm)
由图片可知:
前
上
下
左
右
后
a
a
h
h
b
a
b
b
a
h
b
h
(6×4+6×8+4×8)×2
=104 × 2
=208(dm )
宽是4dm,高是8dm;
长和宽合起来是10dm,
长是10-4=6(dm)。
答:长方体的表面积是208dm 。
课堂小结
表面积
1.长方体或正方体6个面的总面积,叫作它的表面积。
2.长方体的表面积
S表=2ab+2ah+2bh=(ab+ah+bh)×2
正方体的表面积
S表=6a
这节课你有哪些收获?
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
练习
长方体的表面积 S表=2ab+2ah+2bh=(ab+ah+bh)×2
正方体的表面积 S表=6a
重点回顾
练习巩固
1.在展开图上找出相对的面,并用“上、下、前、后、
左 、右”标出,再用a、b、c标出每条棱。
教材第25页练习六
a
b
c
前
上
右
后
左
下
b
a
b
a
b
c
c
c
a
b
b
a
b
c
c
a
c
c
c
2.将下面的展开图围成正方体后,哪两个面分别相对?
晨钟
冬
夏
暮鼓
秋
春
春对
秋对
暮鼓对
夏
冬
晨钟
3.
(1)计算各长方体中前面的面积。
4×2=8(cm )
2×2=4(cm )
2×2.5=5(cm )
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(2)计算各长方体中右侧面的面积。
3×2=6(cm )
3×2=6(cm )
2×2.5=5(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(3)计算各长方体中上面的面积。
4×3=12(cm )
3×2=6(cm )
2×2=4(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(4)计算各长方体的表面积。
4×2×2+3×2×2+3×4×2=52(cm )
2×2×2+3×2×4=32(cm )
2×2.5×4+2×2×2=28(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
4.做一个长5dm、宽4dm、高3dm的长方体布艺
收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
答:至少需要94dm 的布。
=94(dm )
5.一个长方体的饼干盒,长10cm,宽6cm,高12cm。
如果围着它贴一圈商标纸(上、下面不贴),这张
商标纸的面积至少有多少平方厘米?
(10×12+6×12)×2
答:这张商标纸的面积至少有384cm 。
=(120+72)×2
=192×2
上、下面不贴,只贴前、后、左、右四个面,要求这四个面的面积和。
=384(cm )
6. 把一个棱长46cm的正方体纸箱各面都贴上红纸,
作为捐款箱。
(1)至少需要多少平方厘米的红纸?(开口处忽
略不计。)
46×46×6=12696(cm )
答:至少需要12696cm 的红纸。
红纸的面积就是捐款箱的表面积。
46×12=552(cm) 552cm=5.52m
答:一卷4.5m长的胶带纸不够用。
5.52>4.5
6. 把一个棱长46cm的正方体纸箱各面都贴上红纸,
作为捐款箱。
(2)如果只在棱上粘贴一圈胶带纸,一卷4.5m
长的胶带纸够用吗?
7.先根据给出的数据判断物体是正方体还是长方体,
再计算表面积。
图形名称 长 宽 高 表面积
15cm 15cm 10cm
12m 12m 12m
13dm 12dm 10dm
长方体
1050cm
正方体
864m
长方体
812dm
8.一个正方体玻璃鱼缸的棱长为3dm,制作这个鱼
缸至少需要多少平方分米的玻璃?(上面没有盖。)
3×3×5=45(dm )
答:制作这个鱼缸至少需要45dm 的玻璃。
鱼缸没有盖,只有五个面。
9.一个正方体礼品盒的棱长为1.2dm。如果包装这
个礼品盒的用纸是其表面积的1.5倍,至少要用
多少平方分米的包装纸?
1.2×1.2×6×1.5=12.96(dm )
答:至少要用12.96dm 的包装纸。
10.一个新建的游泳池长50m,长是宽的2倍,深2.5m。
现在要在游泳池的四周和底面贴上瓷砖,一共需
要贴多少平方米的瓷砖?
50×25+(50×2.5+25×2.5)×2=1625(m )
答:一共需要贴1625m 的瓷砖。
50÷2=25(m)
11.学校要粉刷教室。已知教室的长是8m,宽是6m,
高是3m,门窗的面积是11.4m 。如果每平方米需
要花6元涂料费,粉刷这个教室需要多少涂料费?
8×6+(8×3+6×3) ×2 11.4=120.6(m )
6×120.6=723.6(元)
答:粉刷这个教室需要723.6元涂料费。
教室底面不用粉刷,需要粉刷上面和前、后、左、右四个面,这五个面的面积减去门窗的面积就是要粉刷的面积。
12.右面这个颁奖台是由3个长方体拼成的。
它的前后两面涂黄色油漆,其他露出来
的面涂红色油漆。涂黄色油漆和红色油
漆的面积各是多少?(单位:cm)
涂黄色油漆的面积:
40×40×2+40×65×2+40×(65 10)×2=12800(cm2)
涂红色油漆的面积:
40×40×3+65×40×2=10000(cm2)
答:涂黄色油漆的面积是12800cm ,
涂红色油漆的面积是10000cm 。
13.如何把这个长方体木块分成两个棱长为4cm的正
方体?这两个正方体的表面积之和与原长方形的
表面积相等吗?
原来长方体的表面积:
两个小正方体的表面积:
8×4×4+4×4×2=160(cm2)
4×4×6×2=192(cm2)
增加的表面积:
192-160=32(cm2)
8cm
4cm
4cm
4cm
4cm
分开后,增加了两个截面,所以两个正方体的总表面积大于原长方体的表面积。表面积增加2个面。
4×4×2=32(cm2)
Thank you!
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
第1课时 长方体、正方体的展开图
1.通过动手操作,知道长方体、正方体的不同的展开图,加深对正方体、长方体特点的认识。
2.经历展开与折叠的活动过程,在想象、操作等活动中,初步感知平面图形与立体图形的关系,发展空间观念。
3.激发学习数学的兴趣,渗透转化思想。
学习目标
【重点】
经历纸盒展开的过程,能在自己的展开图上找到对应的面。
【难点】
能指出其他展开图中相对的面,根据展开图判断能否围成长方体或正方体。
投票箱
晨光小学要举行大队委选举,需要制作一个投票箱(如图)。
应该如何制作呢?
课堂导入
新知探究
把一个长方体或正方体的纸盒展开是什么形状的呢?
要沿着棱剪开。
我展开了一个长方体的纸盒。
正方体的纸盒可以这样展开。
长方体
上面
前面
右面
左面
后面
下面
上面
前面
后面
下面
右面
左面
左面
长方体
上
前
右
左
后
下
观察长方体展开图,回答下面的问题。
(1)哪些面的面积相等?
前面=后面
上面=下面
左面=右面
上
后
右
前
下
a
b
h
a
a
b
b
左
b
h
b
h
a
h
a
h
上
下
左
右
前
后
上、下面:长=长方体的长, 宽=长方体的宽;
左、右面:长=长方体的高, 宽=长方体的宽;
前、后面:长=长方体的长, 宽=长方体的高。
(2)每个面的长和宽与长方体的长、宽、高有什么关系?
上
前
右
左
后
下
上
左
后
右
前
下
长方体的展开图还有可能是怎样的呢?
正方体
上面
前面
右面
左面
后面
下面
上面
前面
右面
左面
后面
下面
正方体
正方体的展开图还有可能是怎样的呢?
“141”型
“231”型
“222”型
“33”型
注意:任何正方体的展开图不能是“田字型”,
也不能是“凹字型”。
1.下列哪些图形是长方体的展开图?在括号内画“√”。
( )
( )
( )
课堂练习
2.下列哪些图形是正方体的展开图?在括号内画“√”。
( )
( )
( )
( )
正方体的展开图不能是“凹字型”,也不能是“田字型”。
3.下面是一幅不完整的正方体展开图。
①
②
③
④
⑤
⑥
(1) 可能在图中的哪个位置。
(2)图中①的对面是( ) ,
②的对面是( )。
⑥
⑤
④
⑥
⑥
(3)如果前面是②,右面是③,
那么上面是( ),下面是( )。
①
⑤
4.把下面这个展开图折成一个长方体。
(1)如果字母A在底部,那么字母( )在上面。
拓展提升
A
B
C
D
F
E
E
4.把下面这个展开图折成一个长方体。
A
B
C
D
F
E
(2)如果字母F在前面,从左边看是字母B,那么字母( )在上面。
E
课堂小结
展开图
1.长方体和正方体展开图的形状不是唯一的,展开的方法不同,得到的展开图不相同。但不管怎样展开,相对的两个面不可能相邻。
2.借助长方体和正方体的展开图可以探究各个面之间的关系。
这节课你有哪些收获?
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
第2课时 长方体、正方体表面积的计算
1.理解长方体和正方体的表面积意义,初步学会计算长方体和正方体表面积的方法。
2.能根据现实情景和信息,通过动手操作、小组合作、观察思考等解决问题的方法,去探求、经历、感受长方体和正方体的表面积概念和计算方法,初步培养探究意识和提升探求能力。
3. 感受到数学与生活的密切联系,培养初步的数学应用意识,并在探究过程中获得积极的数学情感体验。
学习目标
【重难点】
理解表面积的意义,探索长方体和正方体表面积的计算方法,能根据实际情况计算物体的表面积。
长方体或正方体6个面的总面积,叫作它的表面积。
日常生活和生产中,经常需要计算一些长方体或正方体的表面积。
课堂导入
制作尺寸如下图所示的长方体和正方体保温箱,各需要多少平方分米的泡沫板?(单位:dm)
这里要求的是这个长方体和正方体的 。
表面积
新知探究
长方体和正方体6个面的面积之和,叫作它的表面积。
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
新知探究
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
S表
6×5
=148(dm )
6×4
4×5
+
=30+30+24+24+20+20
S上
=
+
S下
S前
S后
S左
S右
+
+
+
+
6×5
6×4
4×5
+
+
+
+
=6×5×2+6×4×2+5×4×2
新知探究
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
=60+48+40
=148(dm2)
新知探究
上、下每个面,长 ,宽 ,面积是 ;
前、后每个面,长 ,宽 ,面积是 ;
左、右每个面,长 ,宽 ,面积是 。
6 dm
5 dm
4 dm
6 dm
5 dm
(6×5)dm2
6 dm
4 dm
(6×4)dm2
5 dm
4 dm
(5×4)dm2
=(6×5+6×4+5×4)×2
=74×2
=148(dm2)
答:需要148平方分米的泡沫板。
长方体的表面积
S表=2ab+2ah+2bh
宽(b)
长(a)
高(h)
S表=(ab+ah+bh)×2
公式推导
=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
新知探究
正方体表面积=棱长×棱长×6
S表=6a
棱长(a)
棱长(a)
棱长(a)
新知探究
棱长(a)
棱长(a)
棱长(a)
=5×5×6
=25×6
=150 (dm2)
答:需要150平方分米的泡沫板。
课堂练习
0.75m
0.5m
1.6m
0.75×1.6×2+0.5×1.6×2+0.75×0.5
=2.4+1.6+0.375
=4.375(m )
答:至少需要4.375 m 的布料。
教材第24页做一做
1. 一个长0.75 m、宽0.5 m、高1.6 m的简易衣柜需要换布罩(如图,没有底面)。至少需要多少平方米布料?
没有底面,这个布罩就只有5个面,要求的就是前后左右面和上面这5个面的面积和。
2. 计算下面长方体的表面积。(单位:dm)
(12×5+12×5+5×5)×2
=145×2
=290(dm )
12×5×4+5×5×2
=240+50
=290(dm )
方法1:
方法2:
12
5
5
答:长方体的表面积是290 dm 。
拓展提升
3. 下面是一个长方体的展开图,求长方体的表面积。(单位:dm)
由图片可知:
前
上
下
左
右
后
a
a
h
h
b
a
b
b
a
h
b
h
(6×4+6×8+4×8)×2
=104 × 2
=208(dm )
宽是4dm,高是8dm;
长和宽合起来是10dm,
长是10-4=6(dm)。
答:长方体的表面积是208dm 。
课堂小结
表面积
1.长方体或正方体6个面的总面积,叫作它的表面积。
2.长方体的表面积
S表=2ab+2ah+2bh=(ab+ah+bh)×2
正方体的表面积
S表=6a
这节课你有哪些收获?
3 长方体和正方体
2.长方体和正方体的表面积
数学人教版五年级下册
练习
长方体的表面积 S表=2ab+2ah+2bh=(ab+ah+bh)×2
正方体的表面积 S表=6a
重点回顾
练习巩固
1.在展开图上找出相对的面,并用“上、下、前、后、
左 、右”标出,再用a、b、c标出每条棱。
教材第25页练习六
a
b
c
前
上
右
后
左
下
b
a
b
a
b
c
c
c
a
b
b
a
b
c
c
a
c
c
c
2.将下面的展开图围成正方体后,哪两个面分别相对?
晨钟
冬
夏
暮鼓
秋
春
春对
秋对
暮鼓对
夏
冬
晨钟
3.
(1)计算各长方体中前面的面积。
4×2=8(cm )
2×2=4(cm )
2×2.5=5(cm )
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(2)计算各长方体中右侧面的面积。
3×2=6(cm )
3×2=6(cm )
2×2.5=5(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(3)计算各长方体中上面的面积。
4×3=12(cm )
3×2=6(cm )
2×2=4(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
(4)计算各长方体的表面积。
4×2×2+3×2×2+3×4×2=52(cm )
2×2×2+3×2×4=32(cm )
2×2.5×4+2×2×2=28(cm )
3.
4cm
3cm
2cm
2cm
3cm
2cm
2cm
2cm
2.5cm
4.做一个长5dm、宽4dm、高3dm的长方体布艺
收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
答:至少需要94dm 的布。
=94(dm )
5.一个长方体的饼干盒,长10cm,宽6cm,高12cm。
如果围着它贴一圈商标纸(上、下面不贴),这张
商标纸的面积至少有多少平方厘米?
(10×12+6×12)×2
答:这张商标纸的面积至少有384cm 。
=(120+72)×2
=192×2
上、下面不贴,只贴前、后、左、右四个面,要求这四个面的面积和。
=384(cm )
6. 把一个棱长46cm的正方体纸箱各面都贴上红纸,
作为捐款箱。
(1)至少需要多少平方厘米的红纸?(开口处忽
略不计。)
46×46×6=12696(cm )
答:至少需要12696cm 的红纸。
红纸的面积就是捐款箱的表面积。
46×12=552(cm) 552cm=5.52m
答:一卷4.5m长的胶带纸不够用。
5.52>4.5
6. 把一个棱长46cm的正方体纸箱各面都贴上红纸,
作为捐款箱。
(2)如果只在棱上粘贴一圈胶带纸,一卷4.5m
长的胶带纸够用吗?
7.先根据给出的数据判断物体是正方体还是长方体,
再计算表面积。
图形名称 长 宽 高 表面积
15cm 15cm 10cm
12m 12m 12m
13dm 12dm 10dm
长方体
1050cm
正方体
864m
长方体
812dm
8.一个正方体玻璃鱼缸的棱长为3dm,制作这个鱼
缸至少需要多少平方分米的玻璃?(上面没有盖。)
3×3×5=45(dm )
答:制作这个鱼缸至少需要45dm 的玻璃。
鱼缸没有盖,只有五个面。
9.一个正方体礼品盒的棱长为1.2dm。如果包装这
个礼品盒的用纸是其表面积的1.5倍,至少要用
多少平方分米的包装纸?
1.2×1.2×6×1.5=12.96(dm )
答:至少要用12.96dm 的包装纸。
10.一个新建的游泳池长50m,长是宽的2倍,深2.5m。
现在要在游泳池的四周和底面贴上瓷砖,一共需
要贴多少平方米的瓷砖?
50×25+(50×2.5+25×2.5)×2=1625(m )
答:一共需要贴1625m 的瓷砖。
50÷2=25(m)
11.学校要粉刷教室。已知教室的长是8m,宽是6m,
高是3m,门窗的面积是11.4m 。如果每平方米需
要花6元涂料费,粉刷这个教室需要多少涂料费?
8×6+(8×3+6×3) ×2 11.4=120.6(m )
6×120.6=723.6(元)
答:粉刷这个教室需要723.6元涂料费。
教室底面不用粉刷,需要粉刷上面和前、后、左、右四个面,这五个面的面积减去门窗的面积就是要粉刷的面积。
12.右面这个颁奖台是由3个长方体拼成的。
它的前后两面涂黄色油漆,其他露出来
的面涂红色油漆。涂黄色油漆和红色油
漆的面积各是多少?(单位:cm)
涂黄色油漆的面积:
40×40×2+40×65×2+40×(65 10)×2=12800(cm2)
涂红色油漆的面积:
40×40×3+65×40×2=10000(cm2)
答:涂黄色油漆的面积是12800cm ,
涂红色油漆的面积是10000cm 。
13.如何把这个长方体木块分成两个棱长为4cm的正
方体?这两个正方体的表面积之和与原长方形的
表面积相等吗?
原来长方体的表面积:
两个小正方体的表面积:
8×4×4+4×4×2=160(cm2)
4×4×6×2=192(cm2)
增加的表面积:
192-160=32(cm2)
8cm
4cm
4cm
4cm
4cm
分开后,增加了两个截面,所以两个正方体的总表面积大于原长方体的表面积。表面积增加2个面。
4×4×2=32(cm2)
Thank you!
