人教版五年级下册4.2真分数和假分数 同步课件(62张PPT)
文档属性
| 名称 | 人教版五年级下册4.2真分数和假分数 同步课件(62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-24 00:00:00 | ||
图片预览






文档简介
(共62张PPT)
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第1课时 真分数和假分数(1)
1. 理解、掌握真分数和假分数的意义和特征,能辨别真分数和假分数。了解带分数的概念,知道带分数是假分数的另一种表示方法。
2. 在数学活动中,提高观察、比较、分析、概括能力,渗透数形结合的思想,进一步发展数感。
学习目标
【重点】
理解、掌握真分数和假分数的意义与特征。
【难点】
建构对假分数意义的理解。
课堂导入
算一算,说一说。
学校有排球12个,篮球11个。篮球的个数是排球的几分之几?排球的个数是篮球的几分之几?
求一个数是另一个数的几分之几,用除法计算。
11
12
11÷12 =
12
11
12÷11 =
这两个问题有什么关系?它们的结果有什么不同?
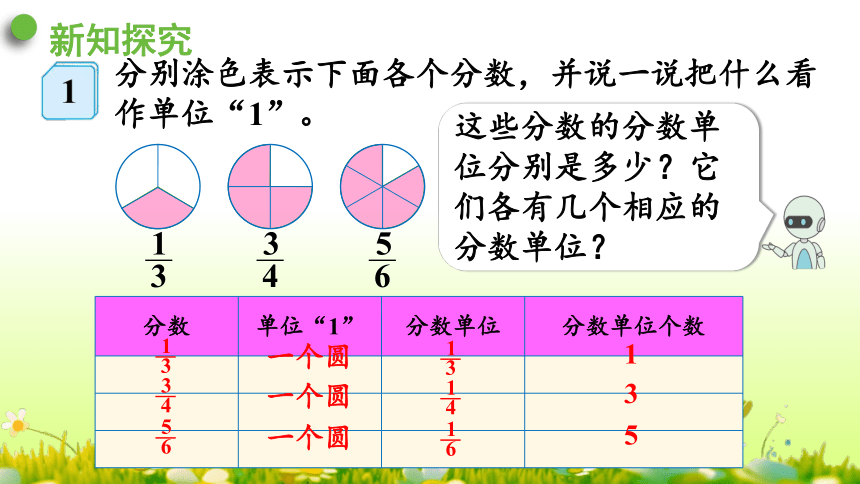
分别涂色表示下面各个分数,并说一说把什么看作单位“1”。
新知探究
3
1
4
3
6
5
这些分数的分数单位分别是多少?它们各有几个相应的分数单位?
分数 单位“1” 分数单位 分数单位个数
3
1
3
1
一个圆
1
4
3
4
1
一个圆
3
6
5
6
1
一个圆
5
3
1
4
3
6
5
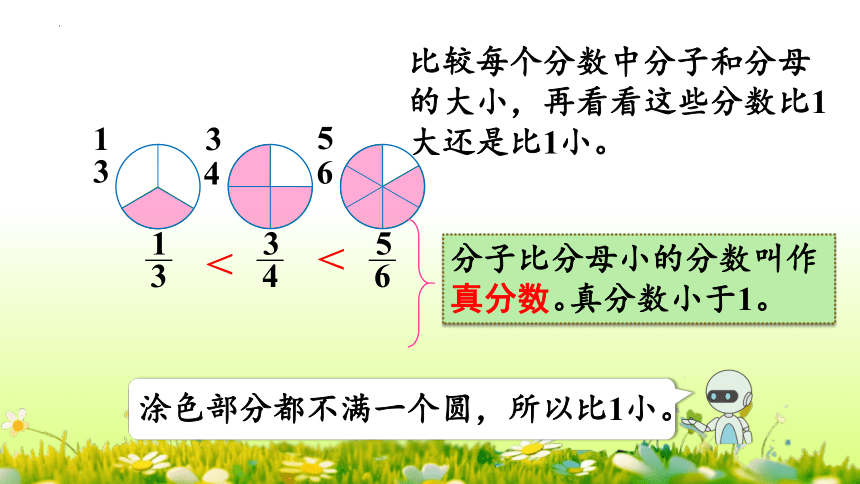
分子比分母小的分数叫作真分数。
比较每个分数中分子和分母的大小,再看看这些分数比1大还是比1小。
1
3
<
3
4
5
6
<
真分数小于1。
涂色部分都不满一个圆,所以比1小。
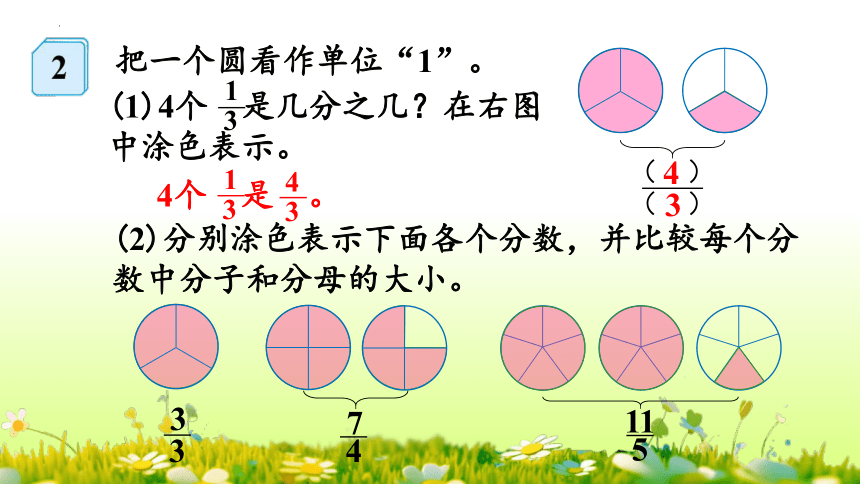
把一个圆看作单位“1”。
(1)4个 是几分之几?在右图中涂色表示。
3
1
( )
( )
4个 是 。
3
1
3
4
3
4
(2)分别涂色表示下面各个分数,并比较每个分数中分子和分母的大小。
3
3
4
7
5
11
3
3
4
7
5
11
( )
( )
3
4
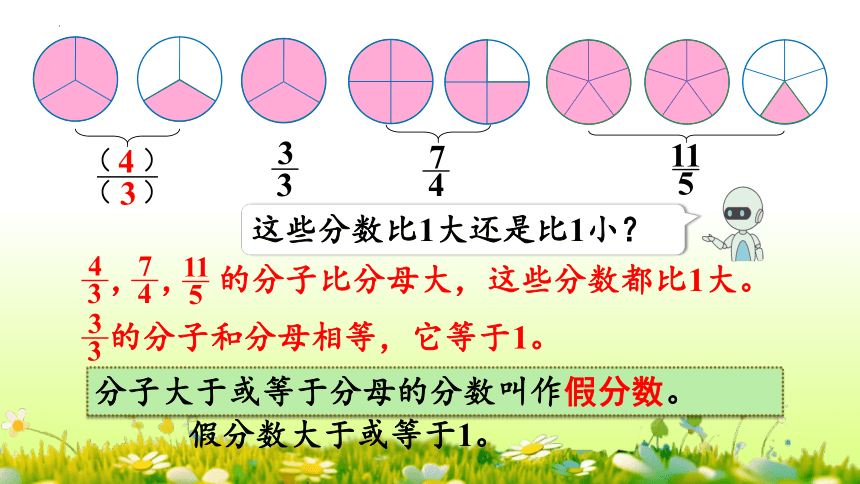
这些分数比1大还是比1小?
, , 的分子比分母大,这些分数都比1大。
3
4
4
7
5
11
的分子和分母相等,它等于1。
3
3
分子大于或等于分母的分数叫作假分数。
假分数大于或等于1。
4
7
5
11
( )
( )
3
4
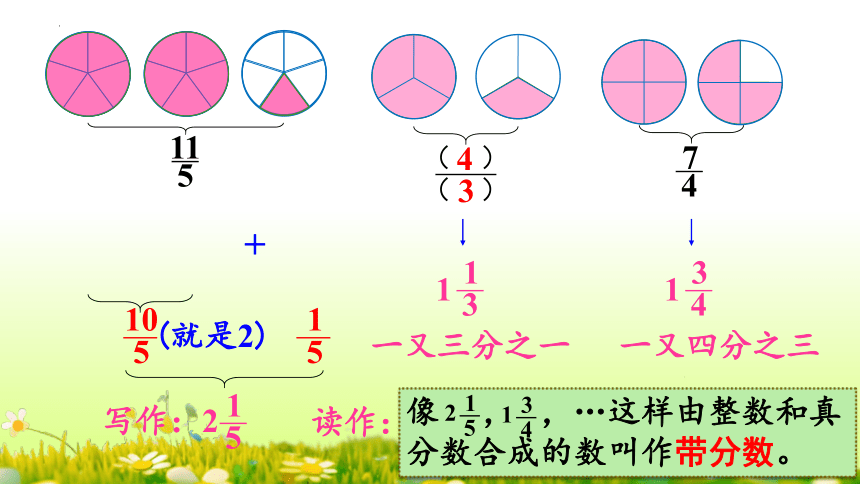
+
5
1
5
10
(就是2)
写作:2
5
1
读作:二又五分之一
1
3
1
1
4
3
一又四分之三
一又三分之一
一又三分之一
像 , ,…这样由整数和真分数合成的数叫作带分数。
2
5
1
1
4
3
举例 概念 与1的大小比较
真分数
假分数
带分数
回顾小结
3
1
4
3
,
…
,
3
3
4
7
,
…
,
3
2
1
5
1
,
…
,
2
分子比分母小的分数叫作真分数。
分子大于或等于分母的分数叫作假分数。
由整数和真分数合成的数叫作带分数。
小于1
大于1或等于1
大于1
根据分子与分母的大小,分数分为真分数和假分数两类,带分数是假分数的另一种表现形式。
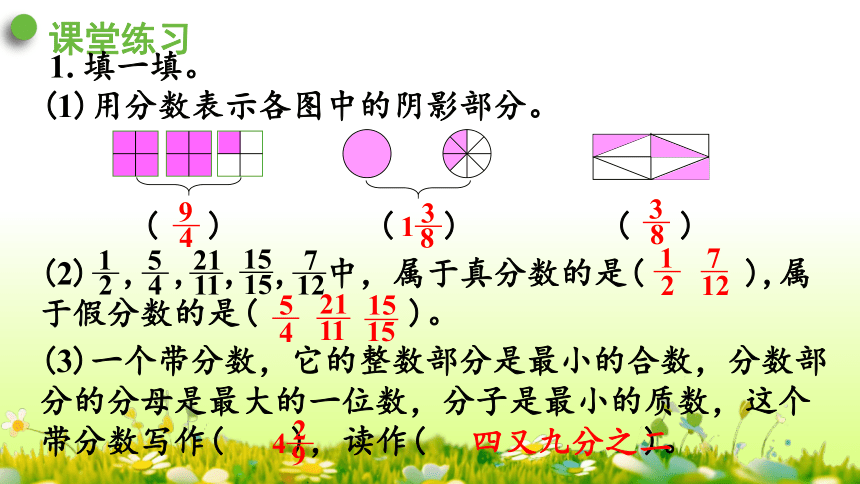
(1)用分数表示各图中的阴影部分。
( ) ( ) ( )
课堂练习
1. 填一填。
4
9
(2) , , , , 中,属于真分数的是( ),属于假分数的是( )。
8
3
1
8
3
11
21
(3)一个带分数,它的整数部分是最小的合数,分数部分的分母是最大的一位数,分子是最小的质数,这个带分数写作( ),读作( )。
2
1
四又九分之二
2
1
4
5
11
21
15
15
12
7
12
7
4
5
15
15
9
2
4
2. 下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
3
1
3
3
3
5
6
1
6
5
6
7
13
6
答: , , 是真分数; , , , 是假分数。
3
1
6
1
6
5
3
3
3
5
6
7
13
6
0
1
2
3
1
3
3
3
5
6
1
6
5
6
7
6
13
教材第54页“做一做”
2. 下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
3
1
3
3
3
5
6
1
6
5
6
7
13
6
看一看,表示真分数的点和表示假分数的点,分别在直线的哪一段上。
0
1
2
3
1
3
3
3
5
6
1
6
5
6
7
6
13
真分数
假分数
真分数可以用直线上0和1之间的点表示,假分数可以用直线上1以及大于1的点表示。
教材第54页“做一做”
3.
下面的说法对吗?为什么?
(教材第55页第2题)
(1)我吃了一个西瓜的 。 ( )
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。 ( )
(3)一块巧克力,我吃了 ,表哥吃了 。 ( )
4
5
5
3
5
2
5
1
6
5
6
1
×
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
×
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
√
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
4. 连一连。
2
2
8
9
6
5
1
4
9
5.
5
7
7÷5 =
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
熊冬眠约 5 个月
睡鼠冬眠约 7 个月
7
5
5÷7 =
答:睡鼠的冬眠时间是熊的 ,熊的冬眠时间是睡鼠的 。
7
5
5
7
规范解答
教材第56页第7题
5.
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
5
7
7÷5 =
7
5
5÷7 =
熊
睡鼠
被除数
除数
除数
被除数
分子
分母
分母
分子
两个问题同属求一个数是另一个数的几分之几或几倍的问题,都是用除法。因为标准量不同,所以除数不同,结果也不同,它们的分子和分母刚好换了一个位置。
对比发现
教材第56页第7题
5.
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
拓展运用
(1)男生人数是女生的 ,则女生人数是男生的 。
( )
( )
6
5
5
6
(2)桃树棵数是梨树的 ,则梨树棵数是桃树的 。
( )
( )
11
12
12
11
教材第56页第7题
提升练习
思路引导
1. 如果 是假分数(x是非0自然数), 是真分数,那么x=( )。
规范解答
答:x = 7。
是假分数
7
x
7
x
8
x
x是大于或等于7的自然数
是真分数
8
x
x是小于8的自然数
x一定是7
7
2 . 一个分数,分子与分母的和是30,如果分子加上8,这个分数就等于1。原来的分数是多少?
思路引导
分子加上8,这个分数就等于1
分子加上8,和就和分母相等
原来分数的分母比分子大8
分子与分母的和是30
列方程求解
2 . 一个分数,分子与分母的和是30,如果分子加上8,这个分数就等于1。原来的分数是多少?
规范解答
解:设原来分数的分子为x ,则原来分数的分母是x +8。
x + x +8 = 30
2x + 8-8 = 30-8
2x = 22
x = 11
x +8 = 11+8 = 19
答:原来的分数是 。
11
19
课堂小结
同学们,这节课你们学会了哪些知识?
真分数、假分数和带分数
一个分数
分子<分母
真分数
分子≥分母
假分数
(小于1)
(大于或等于1)
带分数
(大于1)
由整数和真分数合成的数
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第2课时 真分数和假分数(2)
1. 掌握假分数化成整数或带分数的方法,能正确地把假分数化成整数或带分数。
2. 培养观察、比较、抽象、概括能力,渗透数形结合和转化的数学思想,发展数感。
学习目标
【重点】理解、掌握带分数的意义及特征。
【难点】能正确地把假分数化成整数或带分数。
真分数
假分数
课堂导入
分一分,说一说。
把下面的分数分一分,然后说说各类分数的特征。
1
3
11
12
7
6
5
5
7
13
37
15
1
6
2
33
11
8
9
是不是假分数?
1
6
2
分子比分母小的分数叫做真分数。真分数小于1。
分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于1或等于1。
由整数和真分数合成的数叫做带分数。带分数是假分数的另一种表示方式,带分数都大于1。
涂一涂,说一说。
把下面每个图形看作单位“1”,在图中涂色表示下面的分数,然后看看有什么发现?
12
4
17
6
3
3
=1
=3
=2
6
5
有些假分数的分子恰好是分母的倍数,它们实际上是整数;有些假分数的分子不是分母的倍数,这样的假分数可以写成带分数。
新知探究
(1)把 、 化成整数。
3
3
4
8
方法一
根据分数的意义画图理解。
4
8
1
2
是3个 ,3个 是1,所以 =1。
3
3
3
1
3
3
3
1
3
3
是8个 ,4个 是1,8个 是2,所以 =2。
4
8
4
1
4
1
4
8
4
1
新知探究
方法二
根据分数与除法的关系来计算。
4
8
= 3÷3
3
3
= 1
= 8÷4
= 2
相比而言,方法二简便多了。
假分数的分子恰好是分母的倍数时,那么这个假分数可以化成整数。常用方法:分子除以分母。
(1)把 、 化成整数。
3
3
4
8
(2)把 、 化成带分数。
3
7
5
6
方法一
根据分数的意义画图理解。
3
7
3
1
3
6
=2
是 (就是2)和 合成的数,等于 。
3
7
3
6
3
1
3
1
2
(2)把 、 化成带分数。
3
7
5
6
方法一
根据分数的意义画图理解。
5
6
5
1
5
5
=1
是 (就是1)和 合成的数,等于 。
5
6
5
5
5
1
5
1
1
(2)把 、 化成带分数。
3
7
5
6
方法二
根据分数与除法的关系来计算。
7份里面有2个3份余1份,2个3份是2个整圆,也就是2;余1份就是 ,所以结果是 。
3
1
3
1
2
5
6
= 7÷3
3
7
= 2……1
= 6÷5
= 1……1
6份里面有1个5份余1份,1个5份是1个整圆,也就是1;余1份就是 ,所以结果是 。
5
1
5
1
1
方法分析
(2)把 、 化成带分数。
3
7
5
6
方法二
根据分数与除法的关系来计算。
5
6
= 7÷3
3
7
= 6÷5
解答过程
= 2
3
1
= 1
5
1
= 2……1
= 1……1
余数
分子
商
整数部分
分母不变
商
整数部分
余数
分子
分母不变
假分数的分子不是分母的倍数,那么这个假分数可以化成带分数。常用方法:用分子除以分母,商作为带分数的整数部分,余数作分数部分的分子,分母不变。
回顾小结
假分数
分子是分母的倍数
整数
分子不是分母的倍数
带分数
分子÷分母
没有余数:商
有余数:商
分母
余数
(1) 读作( ),它的分数单位是( ), 它有( )个这样的分数单位,去掉( )个这样的分数单位就是最小的假分数。
课堂练习
1. 填一填。
7
1
(2) , , , , 中,能化成整数的是( ),能化成带分数的是( )。
11
23
(3)已知 (x为非0自然数),当x为( )时,它是真分数;当x为( )时,它是假分数,当x为( )时,它是最小假分数,当x为( )时,它可以化成最小的带分数。
7
7
3
5
7
7
11
23
14
35
12
36
12
36
3
5
14
35
25
7
4
3
三又七分之四
18
9
x
小于9的数
大于或等于9的数
9
10
2. 把下面的假分数化成带分数或整数。
(教材第54页“做一做”)
5
8
21
7
15
2
50
9
43
12
69
20
= 15÷2
= 7
2
1
= 7……1
= 8÷5
= 1
5
3
= 1……3
= 21÷7
= 3
= 50÷9
= 5
9
5
= 5……5
= 43÷12
= 3
12
7
= 3……7
= 69÷20
= 3
20
9
= 3……9
30
15
= 30÷15
= 2
熟练以后,计算过程可以省略哦。
3. 在直线上面的 里填上适当的假分数,下面的 里填上适当的带分数。
(教材第55页第5题)
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
5
2
5
3
5
1
5
2
4.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
你认为带分数和假分数哪个更容易看出数的大小?
一般情况下,将假分数化成带分数或整数再比较容易些。
当然是带分数啦。
(教材第56页第9题)
5. 连一连。
2
6
8
13
6
31
4
19
6
1
5
4
3
4
8
5
1
3
6. 一板药共10粒,每天早、中、晚各1粒。这版药能吃多少天?(用带分数表示。)
教材第55页第4题
求10粒药里面有几个3粒,用除法。
3
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
7.
合唱队有男生19人,女生11人。女生人数是男生的几分之几?男生人数是女生的几倍(用带分数表示)?
19
11
11÷19 =
11
8
=1
11
19
19÷11 =
答:女生人数是男生的 ,男生人数是女生的 倍。
19
11
11
8
1
思路引导
求一个数是另一个数的几分之几或几倍,都是用除法。
规范解答
提升练习
思路引导
1. 在 中,a是非0自然数。当a=( )时, 是分数单位;当a=( )时, 是最小的合数;当a=( )时,
是最小的质数。
5
a
5
a
5
a
5
a
(1)根据分数单位的意义, 的分数单位是 ,因此 a = 1。
5
a
5
1
(2)最小的合数是4,即 = 4,因此,分子 a = 5×4 = 20。
5
a
(3)最小的质数是2,即 = 2,因此,分子 a = 5×2 = 10。
5
a
规范解答
1 20 10
1
20
10
2 . 一个带分数,分数部分的分子是3,把它化成假分数后分子是13。这个带分数可能是多少?
思路引导
带分数的分子是3,化成假分数后分子是13
分析、尝试列举
带分数的整数部分和分母的积是10
带分数的可能情况
规范解答
13-3 =10,
1×10 =10,
2×5 =10,
所以,这个带分数可能是 或 。
10
3
1
5
3
2
答:这个带分数可能是 或 。
10
3
1
5
3
2
课堂小结
同学们,这节课你们学会了哪些知识?
假分数化成整数或带分数
把假分数化成整数或带分数,要用分子除以分母,能整除,商就是整数;不能整除,商是整数部分,余数是分子,分母不变。
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第3课时 分数与除法
重点回顾
做一做,说一说。
(1)
圈出下面分数中的真分数,说一说剩下的假分数哪些可以化成整数,哪些可以化成带分数?
6
5
18
7
5
11
8
53
12
36
2
1
15
31
17
34
4
4
可以化成整数的有:
可以化成带分数的有:
分子是分母的倍数
分子不是分母的倍数
分子比分母小的分数叫作真分数,分子大于或等于分母的分数叫作假分数,假分数可以化成整数或带分数。
(2)将上面的假分数化成整数或带分数。
12
36
17
34
4
4
5
11
8
53
15
31
12
36
=36÷12=3
17
34
=34÷17=2
4
4
=4÷4=1
5
11
=11÷5=2
5
1
8
53
=53÷8=6
8
5
15
31
=31÷15=2
15
1
假分数化成整数或带分数的方法:用假分数的分子除以分母,如果没有余数,结果(商)是整数;如果有余数,结果 是带分数。
分母
余数
(商 )
( )
( )
练习巩固
(教材第55页练习十三)
1.
把一个图形看作单位“1”,用分数表示各图中的涂色部分,再读一读。
4
7
读作:四分之七
6
23
读作:六分之二十三
2.
判断下面的说法是否正确,并说一说你的理由。
(1)我吃了一个西瓜的 。
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。
(3)一块巧克力,我吃了 ,表哥吃了 。
4
5
5
3
5
2
5
1
6
5
6
1
不正确
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
不正确
正确
3÷3 =
3
3
3. 有3杯水。
(1)3个人平均分,每人分 杯,也就是 杯。
( )
( )
(2)2个人平均分,每人分 杯。
3
3
1(杯)
=
3÷2 =
2
3
(杯)
1
2
3
4.一板药共10粒,每天早、中、晚各吃1粒。这板药能吃多少天?(用带分数表示。)
每天吃3粒
求10粒药里面有几个3粒,用除法。
3
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
5.
在直线上面的 里填上适当的假分数,直线下面的
里填上适当的带分数。
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
2
5
2
2
5
3
2
5
1
3
5
2
3
6.
把一个图形看作单位“1”,用分数表示各图中的涂色部分。
2
1
3
( )
( )
3
1
2
7.
5
7
7÷5 =
睡鼠的冬眠时间约是熊的几分之几?
熊的冬眠时间约是睡鼠的几分之几?
7
5
5÷7 =
答:熊的冬眠时间约是睡鼠的 ,睡鼠的冬眠时间约是熊的 。
7
5
5
7
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
真分数是分子比分母小的分数。
(2)写出分子是7的所有假分数。
(1)
分母是7的真分数,其分子一定小于7。
分母可能是1,2,3,4,5,6。
(1)分母是7的真分数有:
7
1
7
2
7
3
7
4
7
5
7
6
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
(2)写出分子是7的所有假分数。
假分数是分子比分母大或分子和分母相等的分数。
(2)
分子是7的假分数,其分母一定等于或小于7。
分子可能是1,2,3,4,5,6,7。
规范解答
(2)分子是7的假分数有:
1
7
2
7
3
7
4
7
5
7
6
7
7
7
9.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
10. 指出下面的分数中哪些是真分数,哪些是假分数。把等于 1 的假分数涂上颜色,看看你有什么发现。
真分数
假分数
=1
<1
>1
发现:真分数的分子比分母小,假分数的分子大于或等于分母,1 可以写成任何非0自然数为分母的分数。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
逐步分解法。
方法一
(1)把30写成两个整数相乘的形式。如:30=2×15。
30
2
15
(2)判断两个因数是不是都是质数。2是质数,不需要再分解;15是合数,需要再分解,15分解成3×5。
3
5
(3)2,3,5都是质数,不需要再分解。
= 2×3×5
拓展提升
解决问题
短除法。
方法二
3 0
2
1 5
(2)用 30 的因数中的质数去除,一般从最小的质数开始,写在短除号左侧,每次除得的商写在短除号的下面。一直除到商是质数为止。
3
5
(3)把30写成除数和最后的商相乘的形式。
30 = 2×3×5
(1)把要分解的30写在短除号 里。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
认识质因数和分解质因数
2
15
3
5
30
= 2×3×5
30 = 2×3×5
3 0
2
1 5
3
5
质数
质数
质数
像 30 = 2×3×5 这样,每个合数都可以写成几个质数相乘的形式,我们就把其中的每个质数叫作这个合数的质因数。把一个合数用质因数相乘的形式表示出来,就叫作分解质因数。
试一试
(1)把12分解质因数,正确的是( )。
12=3×4 B. 12=2×2×3
C. 12=2×6 D. 12=2×2×3×1
合数
合数
不是
质数
B
(2)把下面各数分解质因数。
8
24
75
8
2
4
2
2
8 = 2×2×2
2 4
2
1 2
2
6
24 = 2×2×2×3
2
3
7 5
3
2 5
5
5
75 = 3×5×5
Thank you!
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第1课时 真分数和假分数(1)
1. 理解、掌握真分数和假分数的意义和特征,能辨别真分数和假分数。了解带分数的概念,知道带分数是假分数的另一种表示方法。
2. 在数学活动中,提高观察、比较、分析、概括能力,渗透数形结合的思想,进一步发展数感。
学习目标
【重点】
理解、掌握真分数和假分数的意义与特征。
【难点】
建构对假分数意义的理解。
课堂导入
算一算,说一说。
学校有排球12个,篮球11个。篮球的个数是排球的几分之几?排球的个数是篮球的几分之几?
求一个数是另一个数的几分之几,用除法计算。
11
12
11÷12 =
12
11
12÷11 =
这两个问题有什么关系?它们的结果有什么不同?
分别涂色表示下面各个分数,并说一说把什么看作单位“1”。
新知探究
3
1
4
3
6
5
这些分数的分数单位分别是多少?它们各有几个相应的分数单位?
分数 单位“1” 分数单位 分数单位个数
3
1
3
1
一个圆
1
4
3
4
1
一个圆
3
6
5
6
1
一个圆
5
3
1
4
3
6
5
分子比分母小的分数叫作真分数。
比较每个分数中分子和分母的大小,再看看这些分数比1大还是比1小。
1
3
<
3
4
5
6
<
真分数小于1。
涂色部分都不满一个圆,所以比1小。
把一个圆看作单位“1”。
(1)4个 是几分之几?在右图中涂色表示。
3
1
( )
( )
4个 是 。
3
1
3
4
3
4
(2)分别涂色表示下面各个分数,并比较每个分数中分子和分母的大小。
3
3
4
7
5
11
3
3
4
7
5
11
( )
( )
3
4
这些分数比1大还是比1小?
, , 的分子比分母大,这些分数都比1大。
3
4
4
7
5
11
的分子和分母相等,它等于1。
3
3
分子大于或等于分母的分数叫作假分数。
假分数大于或等于1。
4
7
5
11
( )
( )
3
4
+
5
1
5
10
(就是2)
写作:2
5
1
读作:二又五分之一
1
3
1
1
4
3
一又四分之三
一又三分之一
一又三分之一
像 , ,…这样由整数和真分数合成的数叫作带分数。
2
5
1
1
4
3
举例 概念 与1的大小比较
真分数
假分数
带分数
回顾小结
3
1
4
3
,
…
,
3
3
4
7
,
…
,
3
2
1
5
1
,
…
,
2
分子比分母小的分数叫作真分数。
分子大于或等于分母的分数叫作假分数。
由整数和真分数合成的数叫作带分数。
小于1
大于1或等于1
大于1
根据分子与分母的大小,分数分为真分数和假分数两类,带分数是假分数的另一种表现形式。
(1)用分数表示各图中的阴影部分。
( ) ( ) ( )
课堂练习
1. 填一填。
4
9
(2) , , , , 中,属于真分数的是( ),属于假分数的是( )。
8
3
1
8
3
11
21
(3)一个带分数,它的整数部分是最小的合数,分数部分的分母是最大的一位数,分子是最小的质数,这个带分数写作( ),读作( )。
2
1
四又九分之二
2
1
4
5
11
21
15
15
12
7
12
7
4
5
15
15
9
2
4
2. 下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
3
1
3
3
3
5
6
1
6
5
6
7
13
6
答: , , 是真分数; , , , 是假分数。
3
1
6
1
6
5
3
3
3
5
6
7
13
6
0
1
2
3
1
3
3
3
5
6
1
6
5
6
7
6
13
教材第54页“做一做”
2. 下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
3
1
3
3
3
5
6
1
6
5
6
7
13
6
看一看,表示真分数的点和表示假分数的点,分别在直线的哪一段上。
0
1
2
3
1
3
3
3
5
6
1
6
5
6
7
6
13
真分数
假分数
真分数可以用直线上0和1之间的点表示,假分数可以用直线上1以及大于1的点表示。
教材第54页“做一做”
3.
下面的说法对吗?为什么?
(教材第55页第2题)
(1)我吃了一个西瓜的 。 ( )
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。 ( )
(3)一块巧克力,我吃了 ,表哥吃了 。 ( )
4
5
5
3
5
2
5
1
6
5
6
1
×
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
×
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
√
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
4. 连一连。
2
2
8
9
6
5
1
4
9
5.
5
7
7÷5 =
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
熊冬眠约 5 个月
睡鼠冬眠约 7 个月
7
5
5÷7 =
答:睡鼠的冬眠时间是熊的 ,熊的冬眠时间是睡鼠的 。
7
5
5
7
规范解答
教材第56页第7题
5.
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
5
7
7÷5 =
7
5
5÷7 =
熊
睡鼠
被除数
除数
除数
被除数
分子
分母
分母
分子
两个问题同属求一个数是另一个数的几分之几或几倍的问题,都是用除法。因为标准量不同,所以除数不同,结果也不同,它们的分子和分母刚好换了一个位置。
对比发现
教材第56页第7题
5.
(1)睡鼠的冬眠时间是熊的几分之几?
(2)熊的冬眠时间是睡鼠的几分之几?
拓展运用
(1)男生人数是女生的 ,则女生人数是男生的 。
( )
( )
6
5
5
6
(2)桃树棵数是梨树的 ,则梨树棵数是桃树的 。
( )
( )
11
12
12
11
教材第56页第7题
提升练习
思路引导
1. 如果 是假分数(x是非0自然数), 是真分数,那么x=( )。
规范解答
答:x = 7。
是假分数
7
x
7
x
8
x
x是大于或等于7的自然数
是真分数
8
x
x是小于8的自然数
x一定是7
7
2 . 一个分数,分子与分母的和是30,如果分子加上8,这个分数就等于1。原来的分数是多少?
思路引导
分子加上8,这个分数就等于1
分子加上8,和就和分母相等
原来分数的分母比分子大8
分子与分母的和是30
列方程求解
2 . 一个分数,分子与分母的和是30,如果分子加上8,这个分数就等于1。原来的分数是多少?
规范解答
解:设原来分数的分子为x ,则原来分数的分母是x +8。
x + x +8 = 30
2x + 8-8 = 30-8
2x = 22
x = 11
x +8 = 11+8 = 19
答:原来的分数是 。
11
19
课堂小结
同学们,这节课你们学会了哪些知识?
真分数、假分数和带分数
一个分数
分子<分母
真分数
分子≥分母
假分数
(小于1)
(大于或等于1)
带分数
(大于1)
由整数和真分数合成的数
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第2课时 真分数和假分数(2)
1. 掌握假分数化成整数或带分数的方法,能正确地把假分数化成整数或带分数。
2. 培养观察、比较、抽象、概括能力,渗透数形结合和转化的数学思想,发展数感。
学习目标
【重点】理解、掌握带分数的意义及特征。
【难点】能正确地把假分数化成整数或带分数。
真分数
假分数
课堂导入
分一分,说一说。
把下面的分数分一分,然后说说各类分数的特征。
1
3
11
12
7
6
5
5
7
13
37
15
1
6
2
33
11
8
9
是不是假分数?
1
6
2
分子比分母小的分数叫做真分数。真分数小于1。
分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于1或等于1。
由整数和真分数合成的数叫做带分数。带分数是假分数的另一种表示方式,带分数都大于1。
涂一涂,说一说。
把下面每个图形看作单位“1”,在图中涂色表示下面的分数,然后看看有什么发现?
12
4
17
6
3
3
=1
=3
=2
6
5
有些假分数的分子恰好是分母的倍数,它们实际上是整数;有些假分数的分子不是分母的倍数,这样的假分数可以写成带分数。
新知探究
(1)把 、 化成整数。
3
3
4
8
方法一
根据分数的意义画图理解。
4
8
1
2
是3个 ,3个 是1,所以 =1。
3
3
3
1
3
3
3
1
3
3
是8个 ,4个 是1,8个 是2,所以 =2。
4
8
4
1
4
1
4
8
4
1
新知探究
方法二
根据分数与除法的关系来计算。
4
8
= 3÷3
3
3
= 1
= 8÷4
= 2
相比而言,方法二简便多了。
假分数的分子恰好是分母的倍数时,那么这个假分数可以化成整数。常用方法:分子除以分母。
(1)把 、 化成整数。
3
3
4
8
(2)把 、 化成带分数。
3
7
5
6
方法一
根据分数的意义画图理解。
3
7
3
1
3
6
=2
是 (就是2)和 合成的数,等于 。
3
7
3
6
3
1
3
1
2
(2)把 、 化成带分数。
3
7
5
6
方法一
根据分数的意义画图理解。
5
6
5
1
5
5
=1
是 (就是1)和 合成的数,等于 。
5
6
5
5
5
1
5
1
1
(2)把 、 化成带分数。
3
7
5
6
方法二
根据分数与除法的关系来计算。
7份里面有2个3份余1份,2个3份是2个整圆,也就是2;余1份就是 ,所以结果是 。
3
1
3
1
2
5
6
= 7÷3
3
7
= 2……1
= 6÷5
= 1……1
6份里面有1个5份余1份,1个5份是1个整圆,也就是1;余1份就是 ,所以结果是 。
5
1
5
1
1
方法分析
(2)把 、 化成带分数。
3
7
5
6
方法二
根据分数与除法的关系来计算。
5
6
= 7÷3
3
7
= 6÷5
解答过程
= 2
3
1
= 1
5
1
= 2……1
= 1……1
余数
分子
商
整数部分
分母不变
商
整数部分
余数
分子
分母不变
假分数的分子不是分母的倍数,那么这个假分数可以化成带分数。常用方法:用分子除以分母,商作为带分数的整数部分,余数作分数部分的分子,分母不变。
回顾小结
假分数
分子是分母的倍数
整数
分子不是分母的倍数
带分数
分子÷分母
没有余数:商
有余数:商
分母
余数
(1) 读作( ),它的分数单位是( ), 它有( )个这样的分数单位,去掉( )个这样的分数单位就是最小的假分数。
课堂练习
1. 填一填。
7
1
(2) , , , , 中,能化成整数的是( ),能化成带分数的是( )。
11
23
(3)已知 (x为非0自然数),当x为( )时,它是真分数;当x为( )时,它是假分数,当x为( )时,它是最小假分数,当x为( )时,它可以化成最小的带分数。
7
7
3
5
7
7
11
23
14
35
12
36
12
36
3
5
14
35
25
7
4
3
三又七分之四
18
9
x
小于9的数
大于或等于9的数
9
10
2. 把下面的假分数化成带分数或整数。
(教材第54页“做一做”)
5
8
21
7
15
2
50
9
43
12
69
20
= 15÷2
= 7
2
1
= 7……1
= 8÷5
= 1
5
3
= 1……3
= 21÷7
= 3
= 50÷9
= 5
9
5
= 5……5
= 43÷12
= 3
12
7
= 3……7
= 69÷20
= 3
20
9
= 3……9
30
15
= 30÷15
= 2
熟练以后,计算过程可以省略哦。
3. 在直线上面的 里填上适当的假分数,下面的 里填上适当的带分数。
(教材第55页第5题)
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
5
2
5
3
5
1
5
2
4.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
你认为带分数和假分数哪个更容易看出数的大小?
一般情况下,将假分数化成带分数或整数再比较容易些。
当然是带分数啦。
(教材第56页第9题)
5. 连一连。
2
6
8
13
6
31
4
19
6
1
5
4
3
4
8
5
1
3
6. 一板药共10粒,每天早、中、晚各1粒。这版药能吃多少天?(用带分数表示。)
教材第55页第4题
求10粒药里面有几个3粒,用除法。
3
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
7.
合唱队有男生19人,女生11人。女生人数是男生的几分之几?男生人数是女生的几倍(用带分数表示)?
19
11
11÷19 =
11
8
=1
11
19
19÷11 =
答:女生人数是男生的 ,男生人数是女生的 倍。
19
11
11
8
1
思路引导
求一个数是另一个数的几分之几或几倍,都是用除法。
规范解答
提升练习
思路引导
1. 在 中,a是非0自然数。当a=( )时, 是分数单位;当a=( )时, 是最小的合数;当a=( )时,
是最小的质数。
5
a
5
a
5
a
5
a
(1)根据分数单位的意义, 的分数单位是 ,因此 a = 1。
5
a
5
1
(2)最小的合数是4,即 = 4,因此,分子 a = 5×4 = 20。
5
a
(3)最小的质数是2,即 = 2,因此,分子 a = 5×2 = 10。
5
a
规范解答
1 20 10
1
20
10
2 . 一个带分数,分数部分的分子是3,把它化成假分数后分子是13。这个带分数可能是多少?
思路引导
带分数的分子是3,化成假分数后分子是13
分析、尝试列举
带分数的整数部分和分母的积是10
带分数的可能情况
规范解答
13-3 =10,
1×10 =10,
2×5 =10,
所以,这个带分数可能是 或 。
10
3
1
5
3
2
答:这个带分数可能是 或 。
10
3
1
5
3
2
课堂小结
同学们,这节课你们学会了哪些知识?
假分数化成整数或带分数
把假分数化成整数或带分数,要用分子除以分母,能整除,商就是整数;不能整除,商是整数部分,余数是分子,分母不变。
4 分数的意义和性质
2.真分数和假分数
数学人教版五年级下册
第3课时 分数与除法
重点回顾
做一做,说一说。
(1)
圈出下面分数中的真分数,说一说剩下的假分数哪些可以化成整数,哪些可以化成带分数?
6
5
18
7
5
11
8
53
12
36
2
1
15
31
17
34
4
4
可以化成整数的有:
可以化成带分数的有:
分子是分母的倍数
分子不是分母的倍数
分子比分母小的分数叫作真分数,分子大于或等于分母的分数叫作假分数,假分数可以化成整数或带分数。
(2)将上面的假分数化成整数或带分数。
12
36
17
34
4
4
5
11
8
53
15
31
12
36
=36÷12=3
17
34
=34÷17=2
4
4
=4÷4=1
5
11
=11÷5=2
5
1
8
53
=53÷8=6
8
5
15
31
=31÷15=2
15
1
假分数化成整数或带分数的方法:用假分数的分子除以分母,如果没有余数,结果(商)是整数;如果有余数,结果 是带分数。
分母
余数
(商 )
( )
( )
练习巩固
(教材第55页练习十三)
1.
把一个图形看作单位“1”,用分数表示各图中的涂色部分,再读一读。
4
7
读作:四分之七
6
23
读作:六分之二十三
2.
判断下面的说法是否正确,并说一说你的理由。
(1)我吃了一个西瓜的 。
(2)爷爷把一块菜地的 种了西红柿, 种了茄子, 种了辣椒。
(3)一块巧克力,我吃了 ,表哥吃了 。
4
5
5
3
5
2
5
1
6
5
6
1
不正确
因为一个西瓜平均分成4份,4份全部吃完是这个西瓜的 ,所以吃了 是不可能的。
4
4
4
5
因为一块菜地平均分成5份,3份种西红柿,2份种茄子,地就种满了,种不了辣椒。
因为一块巧克力平均分成6份,我吃了5份,表哥吃了1份,刚好吃完。
不正确
正确
3÷3 =
3
3
3. 有3杯水。
(1)3个人平均分,每人分 杯,也就是 杯。
( )
( )
(2)2个人平均分,每人分 杯。
3
3
1(杯)
=
3÷2 =
2
3
(杯)
1
2
3
4.一板药共10粒,每天早、中、晚各吃1粒。这板药能吃多少天?(用带分数表示。)
每天吃3粒
求10粒药里面有几个3粒,用除法。
3
10
10÷3 =
3
1
=3
答:这板药能吃 天。
3
1
3
(天)
5.
在直线上面的 里填上适当的假分数,直线下面的
里填上适当的带分数。
0
1
2
3
4
5
5
5
10
5
20
5
8
5
12
5
15
5
18
5
1
1
5
4
2
5
3
3
5
6
5
7
5
11
5
13
5
14
5
16
5
17
5
1
2
5
2
2
5
3
2
5
1
3
5
2
3
6.
把一个图形看作单位“1”,用分数表示各图中的涂色部分。
2
1
3
( )
( )
3
1
2
7.
5
7
7÷5 =
睡鼠的冬眠时间约是熊的几分之几?
熊的冬眠时间约是睡鼠的几分之几?
7
5
5÷7 =
答:熊的冬眠时间约是睡鼠的 ,睡鼠的冬眠时间约是熊的 。
7
5
5
7
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
真分数是分子比分母小的分数。
(2)写出分子是7的所有假分数。
(1)
分母是7的真分数,其分子一定小于7。
分母可能是1,2,3,4,5,6。
(1)分母是7的真分数有:
7
1
7
2
7
3
7
4
7
5
7
6
规范解答
8. (1)写出分母是7的所有真分数。
思路引导
(2)写出分子是7的所有假分数。
假分数是分子比分母大或分子和分母相等的分数。
(2)
分子是7的假分数,其分母一定等于或小于7。
分子可能是1,2,3,4,5,6,7。
规范解答
(2)分子是7的假分数有:
1
7
2
7
3
7
4
7
5
7
6
7
7
7
9.
在 里填上“>”“<”或“=”。
9
7
9
7
1
75
25
25
1
3
46
12
4
9
2
8
74
9
<
>
<
=
真分数<1
带分数>1
76
25
3
10
12
3
48
12
74
9
2
9
8
10. 指出下面的分数中哪些是真分数,哪些是假分数。把等于 1 的假分数涂上颜色,看看你有什么发现。
真分数
假分数
=1
<1
>1
发现:真分数的分子比分母小,假分数的分子大于或等于分母,1 可以写成任何非0自然数为分母的分数。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
拓展提升
解决问题
逐步分解法。
方法一
(1)把30写成两个整数相乘的形式。如:30=2×15。
30
2
15
(2)判断两个因数是不是都是质数。2是质数,不需要再分解;15是合数,需要再分解,15分解成3×5。
3
5
(3)2,3,5都是质数,不需要再分解。
= 2×3×5
拓展提升
解决问题
短除法。
方法二
3 0
2
1 5
(2)用 30 的因数中的质数去除,一般从最小的质数开始,写在短除号左侧,每次除得的商写在短除号的下面。一直除到商是质数为止。
3
5
(3)把30写成除数和最后的商相乘的形式。
30 = 2×3×5
(1)把要分解的30写在短除号 里。
每个合数都可以由几个质数相乘得到。例如:4=2×2,
15=3×5……你能把30写成几个质数相乘的形式吗?
认识质因数和分解质因数
2
15
3
5
30
= 2×3×5
30 = 2×3×5
3 0
2
1 5
3
5
质数
质数
质数
像 30 = 2×3×5 这样,每个合数都可以写成几个质数相乘的形式,我们就把其中的每个质数叫作这个合数的质因数。把一个合数用质因数相乘的形式表示出来,就叫作分解质因数。
试一试
(1)把12分解质因数,正确的是( )。
12=3×4 B. 12=2×2×3
C. 12=2×6 D. 12=2×2×3×1
合数
合数
不是
质数
B
(2)把下面各数分解质因数。
8
24
75
8
2
4
2
2
8 = 2×2×2
2 4
2
1 2
2
6
24 = 2×2×2×3
2
3
7 5
3
2 5
5
5
75 = 3×5×5
Thank you!
