4.约分 (课件)-数学人教版五年级下册(共62张PPT)
文档属性
| 名称 | 4.约分 (课件)-数学人教版五年级下册(共62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览








文档简介
(共62张PPT)
4 分数的意义和性质
4.约分
数学人教版五年级下册
第1课时 分数的产生和意义
1. 理解两个数的公因数和最大公因数的意义。掌握求两个数的公因数和最大公因数的方法,能熟练地求两个数的最大公因数。
2. 结合具体例题,培养学生观察、分析、抽象、归纳等能力。
3. 激发学生的学习积极性,发展积极的学科情感。
学习目标
【重难点】
掌握求两个数的公因数和最大公因数的方法。
课堂导入
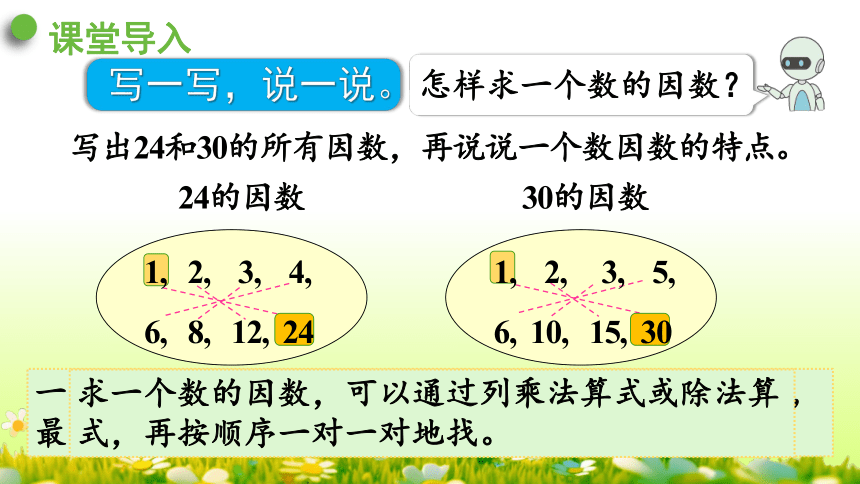
写一写,说一说。
写出24和30的所有因数,再说说一个数因数的特点。
怎样求一个数的因数?
24的因数
30的因数
一个数因数的个数是有限的。其中,最小的因数是1,最大的因数是它本身。
求一个数的因数,可以通过列乘法算式或除法算式,再按顺序一对一对地找。
1, 2, 3, 4,
6, 8, 12, 24
1, 2, 3, 5,
6, 10, 15, 30
新知探究
(教材第60页例1)
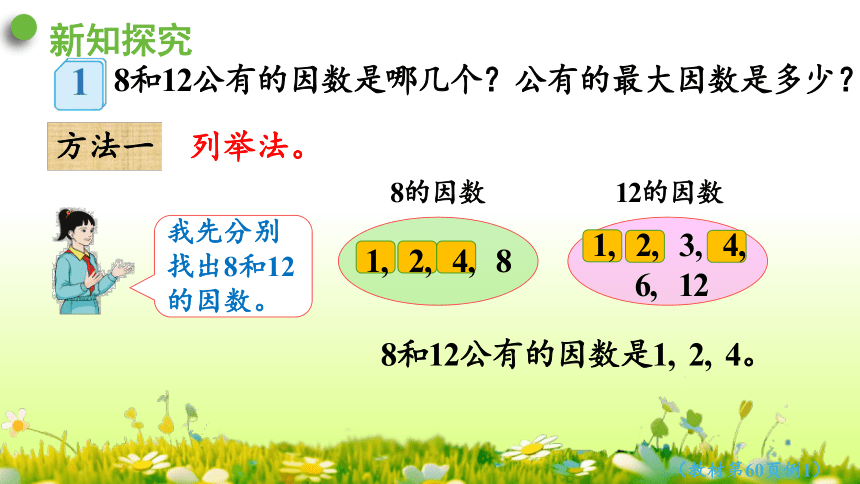
8和12公有的因数是哪几个?公有的最大因数是多少?
我先分别找出8和12的因数。
8的因数
12的因数
8和12公有的因数是1, 2, 4。
1, 2, 4, 8
方法一
列举法。
1, 2, 3, 4,
6, 12
还可以这样表示。
8的因数
12的因数
8
3, 6,
12
方法二
集合法。
8和12公有的因数
1, 2, 4是8和12公有的因数,叫作它们的公因数。其中,4是最大的公因数,叫作它们的最大公因数。
8和12公有的因数是1, 2, 4;公有的最大因数是4。
1, 2,
4
(教材第60页例1)
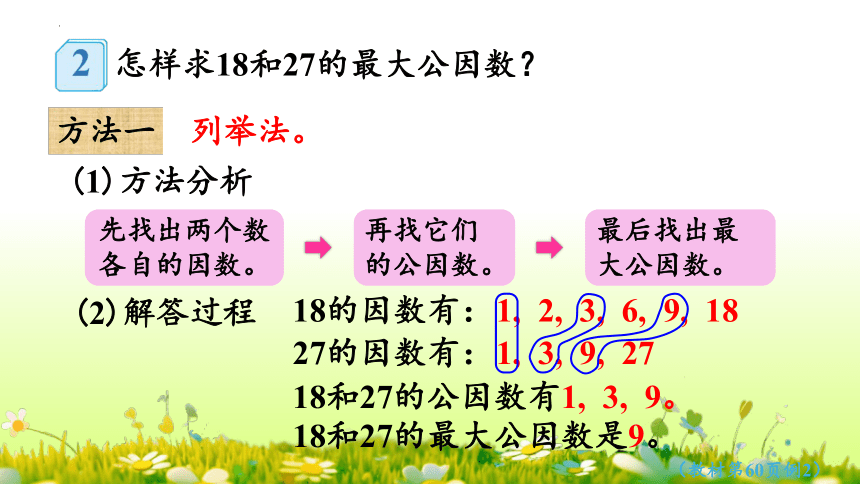
怎样求18和27的最大公因数?
方法一
列举法。
(1)方法分析
先找出两个数各自的因数。
再找它们的公因数。
最后找出最大公因数。
(2)解答过程
18的因数有:
1, 2, 3, 6, 9, 18
27的因数有:
1, 3, 9, 27
18和27的公因数有1, 3, 9。
18和27的最大公因数是9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法二
筛选法。
(1)方法分析
先找出一个数的因数。
再从中找出另一个数的因数。
最后找出最大公因数。
(2)解答过程
18的因数有:
1, 2, 3, 6, 9, 18
在18的因数中,
1, 3, 9也是27的因数。
18和27的最大公因数是9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法三
分解质因数法。
(1)方法分析
先分别把18和27分解质因数,将公有的质因数相乘,所得的积就是这两个数的最大公因数。
(2)解答过程
18 = 2×3×3
27 = 3×3×3
3
3
公有的质因数
3
3
18和27的最大公因数是3×3=9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法四
短除法。
(1)方法分析
用18和27公有的质因数连续去除,除到两个数的商只有公因数1为止,然后把所有的除数相乘,所得的积就是它们的最大公因数。
(2)解答过程
18
27
3
3
用公有的质因数3除
6
9
2
3
用公有的质因数3除
除到两个商只有公因数1为止
18和27的最大公因数是3×3=9。
(教材第60页例2)
你知道吗?
利用分解质因数的方法,可以比较简便地求出两个数的最大公因数。例如:
24=2×2×2×3
36=2×2×3×3
24和36的最大公因数:
2×2×3=12
24
36
2
12
18
2
6
9
3
2
3
…用公有的质因数2除
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公
因数1为止
24和36的最大公因数:
2×2×3=12
为了简便,通常写成右侧的形式。
可记作:(24,36)=12
怎样求18和27的最大公因数?
18和27的公因数有1, 3, 9;最大公因数是9。
讨论一下,两个数的公因数和它们的最大公因数之间有什么关系?
公因数1, 3, 9
最大公因数 9
因数
倍数
两个数的公因数是它们最大公因数的因数,最大公因数是公因数的倍数。
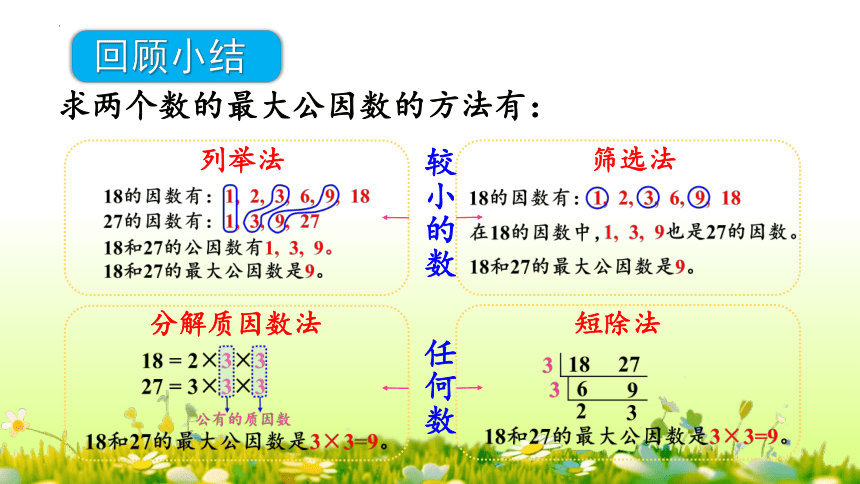
回顾小结
列举法
筛选法
分解质因数法
短除法
求两个数的最大公因数的方法有:
较小的数
任何数
课堂练习
1. 把16和24的因数、公因数分别填入相应的位置,再圈出它们的最大公因数。
16的因数
24的因数
16的因数
24的因数
1
2
4
8
16
1
2
3
4
6
8
12
24
1
2
4
8
16
3
6
12
24
16和24的公因数
(教材第61页“做一做”)
12的因数
18的因数
1
2
3
6
4
12
9
18
12和18的公因数
答:4、12是12的因数而不是18的因数,9、18是18的因数而不是12的因数,1、2、3、6是12和18的公因数。
2. 下面哪些数是12的因数而不是18的因数?哪些数是18的因数而不是12的因数?哪些数是12和18的公因数?
1 2 3 4 6 9 12 18
(教材第61页“做一做”)
3. 找出下面每组数的最大公因数。你发现了什么?
4和8
12和36
4的因数有:1, 2, 4
8的因数有:1, 2, 4, 8
4和8的最大公因数是4。
12的因数有:1, 2, 3, 4, 6, 12
12的因数也都是36的因数。
12和36的最大公因数是12。
1和7
8和9
1和7的最大公因数是1。
8和9的最大公因数是1。
(教材第61页“做一做”)
3. 找出下面每组数的最大公因数。你发现了什么?
12和35
12 和 35的最大公因数是1。
如果一个数是另一个数的倍数,那么较小数是这两个数的最大公因数。如果两个数的公因数只有1,那么它们的最大公因数也是 1 。
(教材第61页“做一做”)
5和11
5 和 11的最大公因数是1。
(2)一个自然数的最小倍数和最大因数都是12,这个数是( ),这个数和 18的公因数有( )个,最大公因数是( )。
(1)18的因数有( ),24的因数有(
),18和24的公因数有( );最大公因数是( )。
4. 填一填。
(3)在括号里填一个数,使它和已知数的公因数只有1。
9和( ) 16和( ) ( )和13。
1, 2, 3,
1, 2, 3, 6, 9, 18
1, 2, 3, 6
6
12
4
4, 6, 8, 12, 24
6
10
17
12
5. 先在第一列各数对应的因数下面画“√”,再填空。
(教材第63页第3题)
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
(1)8和16的公因数有 ,最大公因数是 。
(2)8和20的公因数有 ,最大公因数是 。
(3)16和20的公因数有 ,最大公因数是 。
(4)8、16和20的公因数有 ,最大公因数是 。
1
, 2
, 4
, 8
8
1
, 2
, 4
4
1
, 2
, 4
4
1
, 2
, 4
4
提升练习
1. 你能用短除法求出下面每组数的最大公因数吗?
30和45
16和40
30
45
5
3
6
9
2
3
16
40
2
2
8
20
4
10
2
2
5
30和45的最大公因数是5×3=15。
12和36的最大公因数是2×2×2=8。
2 . 写出下列各数与3的最大公因数,你有什么发现?
2 3 4 6 11 12 14
与3的最大公因数
3
1
1
1
1
3
3
我发现:当一个数是给定质数的倍数时,它们的最大公因数是( );当一个数不是给定质数的倍数时,它们的最大公因数是( );一个数与质数的最大公因数只有( )种情况。
质数本身
1
两
课堂小结
同学们,这节课你们学会了哪些知识?
公因数和最大公因数
几个数公有的因数,叫做这几个数的公因数;其中最大的一个公因数,叫做这几个数的最大公因数。
求两个数的最大公因数,常用的方法有:列举法、筛选法、分解质因数法和短除法。
4 分数的意义和性质
4.约分
数学人教版五年级下册
第2课时 分数与除法
新知探究
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用一种边长整分米数的正方形地砖将储藏室的地面铺满(用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
阅读与理解
16 dm
12 dm
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块)
整块正方形地砖正好铺满
可以选择边长是几分米的地砖?边长最大是几分米?
dm
边长最大是几分米?
地面长16 dm,宽12 dm。
用边长 1 dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
可以画图来探究。
16 dm
12 dm
长边:16÷1=16(块)
1 dm
1 dm
宽边:12÷1=12(块)
分析与解答
用边长 2 dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
16 dm
12 dm
长边:16÷2=8(块)
2 dm
2dm
宽边:12÷2=6(块)
分析与解答
用边长 3dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
16 dm
12 dm
长边:16÷3=5(块)……1
宽边:12÷3=4(块)
分析与解答
3dm
3dm
分析与解答
要使所用的地砖都是整块的,地砖的边长必须是12和16的公因数。
想一想:为什么边长是1dm、2dm的正方形地砖能铺满贮藏室地面,而边长是3dm的正方形地砖不能呢?
因为1、2是12和16的公因数,而3是12的因数,不是16的因数。
只要找出16和12的公因数和最大公因数,就能求出正方形地砖的边长以及最大边长是多少。
分析与解答
16的因数有:1, 2, 4, 8, 16
12的因数有:1, 2, 3, 4, 6, 12
12和16的公因数有:1, 2, 4。最大公因数是4。
所以,可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用边长是整分米数的正方形地砖将储藏室的地面铺满(使用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
12和16的公因数有:1, 2, 4。最大公因数是4。
答:可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
规范解答
回顾小结
在铺地砖问题中,要使地面铺满且使用的地砖都是整块,就是求长和宽的公因数;求地砖的边长最大是多少,就是求长和宽的最大公因数。
当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
课堂练习
(教材第63页第5题)
正方形的边长必须是70和50的公因数。
就是求70和50的最大公因数。
70的因数有:1,2 ,5 ,7 ,10,14, 35,70
50的因数有:1,2, 5,10,25,50
70和50的公因数有1,2,5,10,最大公因数是10。
答:剪出的正方形的边长最大是10厘米。
1. 有一张长方形纸,长70cm,宽50cm。如果要剪成若干张同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?
(2)两个连续自然数的和是23,这两个数的最大公因数是( )。
(1)5和7的最大公因数是( )。
2. 填一填。
(3)如果a=5b(且b>5),那么a与b的最大公因数是( )。
1
1
b
(4)1和任意非零自然数的最大公因数是( )。
1
(2) 24是48和96的( )。
A.因数 B.公因数 C.最大公因数
(1)既有公因数2又有公因数3的一组数是( )。
A.30和12 B.16和25 C.14和15
3. 选一选。
(3)甲数和乙数是两个连续的自然数(甲、乙都不为0),它们的最大公因数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
B
A
每排人数必须是48和36的公因数。
就是求48和36的最大公因数。
思路引导
先求出每排最多有多少人,再分别算出男、女生有几排。
4. 男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
规范解答
36
48
2
2
18
24
9
12
3
3
4
36和48的最大公因数是2×2×3=12。
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男生有4排,女生有3排。
4. 男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
16的因数有:1,2 ,4 ,8 ,16
12的因数有:1,2 ,3 ,4 ,6, 12
1.要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米?
12 cm
16 cm
44 cm
每段木棒的长度必须是12、16和44的公因数。
就是求12、16和44的最大公因数。
44的因数有:1,2 ,4 ,11,22, 44
12、16和44的公因数有:1,2 ,4,最大公因数是4。
答:每段最长是 4 厘米。
提升练习
(教材第64页第11*题)
2 . 把46块水果糖和38块巧克力分别平均分给几个小朋友。结果水果糖剩1块,巧克力剩3块,你知道最多有多少个小朋友吗?
思路引导
46块水果糖平均分给小朋友后,剩1块。
45块水果糖可以正好分完。
38块巧克力平均分给小朋友后,剩3块。
35块巧克力可以正好分完。
求小朋友最多有多少个,就是求45和35的最大公因数。
2 . 把46块水果糖和38块巧克力分别平均分给几个小朋友。结果水果糖剩1块,巧克力剩3块,你知道最多有多少个小朋友吗?
规范解答
46-1=45(块)
38-3=35(块)
45
35
5
9
7
45和35的最大公因数是5,即最多有5个小朋友。
答:最多有5个小朋友。
课堂小结
同学们,这节课你们学会了哪些知识?
公因数和最大公因数的应用
在铺地砖问题中,要使地面铺满且使用的地砖是整块时,就是求长和宽的公因数;要求地砖的边长最大是多少,就是求长和宽的最大公因数。
4 分数的意义和性质
4.约分
数学人教版五年级下册
第3课时 分数与除法
1. 理解约分和最简分数的意义,进一步加深对分数的基本性质、公因数、最大公因数的认识。探究并掌握约分的方法,能灵活运用所学知识正确约分。
2. 在活动中提升学生的观察操作能力、归纳概括能力。
3. 积累数学活动经验,体验数学学习的乐趣。
学习目标
【重点】
归纳、概括出最简分数的概念及约分的方法。
【难点】
理解约分的意义,掌握约分的方法。
课堂导入
在括号里填上适当的数。
32
20
( )
8
=
9
6
( )
3
=
5
2
24
18
( )
3
=
4
这是根据什么?
分数的基本性质:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
÷4
÷4
÷3
÷3
÷6
÷6
把下面各分数中分子和分母的最大公因数填在括号里。
8
7
( )
36
24
( )
20
15
( )
26
13
( )
1
12
5
13
新知探究
(教材第65页例4)
把 化成分子和分母比较小且分数大小不变的分数。
30
24
你是怎么考虑的?
利用分数的基本性质。
30
24
=
30÷2
24÷2
=
15
12
方法一
用分子和分母的公因数( 1 除外)去除。
15
12
=
15÷3
12÷3
=
5
4
把 化成分子和分母比较小且分数大小不变的分数。
30
24
=
30÷2
24÷2
=
15
12
方法一
用分子和分母的公因数( 1 除外)去除。
15
12
=
15÷3
12÷3
=
5
4
30
24
想一想:有没有更简便的方法?
方法二
用分子和分母的最大公因数去除。
30
24
=
30÷6
24÷6
=
5
4
30
24
15
12
5
4
=
变小
变小
变小
变小
=
像这样,把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。
同样是约分,把 约成 和 有什么不同?
30
24
15
12
5
4
15
12
5
4
分子分母的公因数还有3,还能继续除。
分子分母的公因数只有1,不能继续除。
的分子和分母只有公因数 1 , 像这样的分数叫作最简分数。
5
4
约分时,通常要约成最简分数。
30
24
=
30÷2
24÷2
=
15
12
15
12
=
15÷3
12÷3
=
5
4
30
24
=
30÷6
24÷6
=
5
4
约分时也可以这样写:
30
24
12
15
4
5
=
5
4
÷2
÷3
30
24
4
5
=
5
4
÷6
逐次约分法
一次约分法
回顾小结
与原来的分数相比,约分后的分数大小不变,但分子、分母都变小了。
约分时,每次都要用分子、分母的公因数或最大公因数去除。通常要约成分子和分母只有公因数1(互质)的最简分数。
课堂练习
(教材第65页“做一做”)
1. 下列分数中哪些是最简分数?把不是最简分数的化成最简分数。
16
15
21
10
30
17
45
20
91
31
18
4
11
6
48
12
15
9
45
20
4
9
=
9
4
÷5
18
4
2
9
=
9
2
÷2
48
12
1
4
=
4
1
÷12
15
9
3
5
=
5
3
÷3
2. 把上下两行相等的两个分数用线连起来。
7
3
6
4
5
2
8
6
9
3
21
9
4
3
3
1
25
10
3
2
(教材第65页“做一做”)
(2)分数 的分子和分母的最大公因数是( ) ,化成最简分数是( )。
(1)一个分数约分后,分数的大小( )。
3. 填一填。
(3)分母是 8 的最简真分数的和是( )。
不变
3
2
(4)一个最简真分数,分子和分母的积是7,这个分数是( )。
27
6
9
2
7
1
4. 在 里填上“>”“<”或“=”。
32
8
4
3
9
6
3
1
5
3
10
8
7
5
21
15
25
5
5
1
8
3
24
21
1
4
<
2
3
<
4
5
>
5
7
=
1
5
=
7
8
<
5. 在括号里填上最简分数。
8分米=( )米
450千克=( )吨
250毫升=( )升
150平方分米=( )平方米
35秒=( )分
2800平方米=( )公顷
8÷10=
8
10
4
5
=
5
4
450÷1000=
450
1000
9
20
=
20
9
250÷1000=
250
1000
1
4
=
4
1
2800÷10000=
2800
10000
7
25
=
25
7
150÷100=
150
100
3
2
=
2
3
35÷60=
35
60
7
12
=
12
7
(教材第66页第5题)
6. 兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
标准量。
80张
照片总数
喜欢的35张
占几分之几
其他的
占几分之几
思路引导
求一个数是另一个数的几分之几,用除法。分别表示出喜欢的照片和其他的照片各占总数的几分之几,再约分化简。
6. 兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
80张
照片总数
喜欢的35张
占几分之几
其他的
占几分之几
规范解答
35÷80 =
80
35
7
16
=
16
7
(80-35)÷80 =
80
45
9
16
=
16
9
答: 兰兰喜欢的照片和其他的照片分别占照片总数的 和 。
16
9
16
7
(教材第66页第5题)
提升练习
1. 化简一个分数时,用2约了两次,用3约了一次,得
。求原来的分数。
本题可用倒推法求解。
(教材第67页第13*题)
8
3
思路引导
( )÷2÷2÷3
( )÷2÷2÷3
=
8
3
÷2
÷2
÷2
÷2
÷3
÷3
×3
×3
×2
×2
×2
×2
8
3
24
9
=
48
18
96
36
=
×3
×3
=
×2
×2
×2
×2
提升练习
1. 化简一个分数时,用2约了两次,用3约了一次,得
。求原来的分数。
8
3
规范解答
3×3×2×2
8×3×2×2
=
96
36
答:原来的分数是 。
96
36
(教材第67页第13*题)
2 . 把 约成最简分数。
思路引导
分子、分母的最大公因数是100010001
分子、分母同时除以100010001就可得到最简分数。
202020202020
202120212021
202020202020
202120212021
分子202020202020=2020×100010001
分母202120212021=2021×100010001
规范解答
=
2020×100010001
2021×100010001
=
2021
2020
课堂小结
同学们,这节课你们学会了哪些知识?
约分
把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。分子和分母只有公因数1的分数,叫作最简分数。
Thank you!
4 分数的意义和性质
4.约分
数学人教版五年级下册
第1课时 分数的产生和意义
1. 理解两个数的公因数和最大公因数的意义。掌握求两个数的公因数和最大公因数的方法,能熟练地求两个数的最大公因数。
2. 结合具体例题,培养学生观察、分析、抽象、归纳等能力。
3. 激发学生的学习积极性,发展积极的学科情感。
学习目标
【重难点】
掌握求两个数的公因数和最大公因数的方法。
课堂导入
写一写,说一说。
写出24和30的所有因数,再说说一个数因数的特点。
怎样求一个数的因数?
24的因数
30的因数
一个数因数的个数是有限的。其中,最小的因数是1,最大的因数是它本身。
求一个数的因数,可以通过列乘法算式或除法算式,再按顺序一对一对地找。
1, 2, 3, 4,
6, 8, 12, 24
1, 2, 3, 5,
6, 10, 15, 30
新知探究
(教材第60页例1)
8和12公有的因数是哪几个?公有的最大因数是多少?
我先分别找出8和12的因数。
8的因数
12的因数
8和12公有的因数是1, 2, 4。
1, 2, 4, 8
方法一
列举法。
1, 2, 3, 4,
6, 12
还可以这样表示。
8的因数
12的因数
8
3, 6,
12
方法二
集合法。
8和12公有的因数
1, 2, 4是8和12公有的因数,叫作它们的公因数。其中,4是最大的公因数,叫作它们的最大公因数。
8和12公有的因数是1, 2, 4;公有的最大因数是4。
1, 2,
4
(教材第60页例1)
怎样求18和27的最大公因数?
方法一
列举法。
(1)方法分析
先找出两个数各自的因数。
再找它们的公因数。
最后找出最大公因数。
(2)解答过程
18的因数有:
1, 2, 3, 6, 9, 18
27的因数有:
1, 3, 9, 27
18和27的公因数有1, 3, 9。
18和27的最大公因数是9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法二
筛选法。
(1)方法分析
先找出一个数的因数。
再从中找出另一个数的因数。
最后找出最大公因数。
(2)解答过程
18的因数有:
1, 2, 3, 6, 9, 18
在18的因数中,
1, 3, 9也是27的因数。
18和27的最大公因数是9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法三
分解质因数法。
(1)方法分析
先分别把18和27分解质因数,将公有的质因数相乘,所得的积就是这两个数的最大公因数。
(2)解答过程
18 = 2×3×3
27 = 3×3×3
3
3
公有的质因数
3
3
18和27的最大公因数是3×3=9。
(教材第60页例2)
怎样求18和27的最大公因数?
方法四
短除法。
(1)方法分析
用18和27公有的质因数连续去除,除到两个数的商只有公因数1为止,然后把所有的除数相乘,所得的积就是它们的最大公因数。
(2)解答过程
18
27
3
3
用公有的质因数3除
6
9
2
3
用公有的质因数3除
除到两个商只有公因数1为止
18和27的最大公因数是3×3=9。
(教材第60页例2)
你知道吗?
利用分解质因数的方法,可以比较简便地求出两个数的最大公因数。例如:
24=2×2×2×3
36=2×2×3×3
24和36的最大公因数:
2×2×3=12
24
36
2
12
18
2
6
9
3
2
3
…用公有的质因数2除
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公
因数1为止
24和36的最大公因数:
2×2×3=12
为了简便,通常写成右侧的形式。
可记作:(24,36)=12
怎样求18和27的最大公因数?
18和27的公因数有1, 3, 9;最大公因数是9。
讨论一下,两个数的公因数和它们的最大公因数之间有什么关系?
公因数1, 3, 9
最大公因数 9
因数
倍数
两个数的公因数是它们最大公因数的因数,最大公因数是公因数的倍数。
回顾小结
列举法
筛选法
分解质因数法
短除法
求两个数的最大公因数的方法有:
较小的数
任何数
课堂练习
1. 把16和24的因数、公因数分别填入相应的位置,再圈出它们的最大公因数。
16的因数
24的因数
16的因数
24的因数
1
2
4
8
16
1
2
3
4
6
8
12
24
1
2
4
8
16
3
6
12
24
16和24的公因数
(教材第61页“做一做”)
12的因数
18的因数
1
2
3
6
4
12
9
18
12和18的公因数
答:4、12是12的因数而不是18的因数,9、18是18的因数而不是12的因数,1、2、3、6是12和18的公因数。
2. 下面哪些数是12的因数而不是18的因数?哪些数是18的因数而不是12的因数?哪些数是12和18的公因数?
1 2 3 4 6 9 12 18
(教材第61页“做一做”)
3. 找出下面每组数的最大公因数。你发现了什么?
4和8
12和36
4的因数有:1, 2, 4
8的因数有:1, 2, 4, 8
4和8的最大公因数是4。
12的因数有:1, 2, 3, 4, 6, 12
12的因数也都是36的因数。
12和36的最大公因数是12。
1和7
8和9
1和7的最大公因数是1。
8和9的最大公因数是1。
(教材第61页“做一做”)
3. 找出下面每组数的最大公因数。你发现了什么?
12和35
12 和 35的最大公因数是1。
如果一个数是另一个数的倍数,那么较小数是这两个数的最大公因数。如果两个数的公因数只有1,那么它们的最大公因数也是 1 。
(教材第61页“做一做”)
5和11
5 和 11的最大公因数是1。
(2)一个自然数的最小倍数和最大因数都是12,这个数是( ),这个数和 18的公因数有( )个,最大公因数是( )。
(1)18的因数有( ),24的因数有(
),18和24的公因数有( );最大公因数是( )。
4. 填一填。
(3)在括号里填一个数,使它和已知数的公因数只有1。
9和( ) 16和( ) ( )和13。
1, 2, 3,
1, 2, 3, 6, 9, 18
1, 2, 3, 6
6
12
4
4, 6, 8, 12, 24
6
10
17
12
5. 先在第一列各数对应的因数下面画“√”,再填空。
(教材第63页第3题)
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
(1)8和16的公因数有 ,最大公因数是 。
(2)8和20的公因数有 ,最大公因数是 。
(3)16和20的公因数有 ,最大公因数是 。
(4)8、16和20的公因数有 ,最大公因数是 。
1
, 2
, 4
, 8
8
1
, 2
, 4
4
1
, 2
, 4
4
1
, 2
, 4
4
提升练习
1. 你能用短除法求出下面每组数的最大公因数吗?
30和45
16和40
30
45
5
3
6
9
2
3
16
40
2
2
8
20
4
10
2
2
5
30和45的最大公因数是5×3=15。
12和36的最大公因数是2×2×2=8。
2 . 写出下列各数与3的最大公因数,你有什么发现?
2 3 4 6 11 12 14
与3的最大公因数
3
1
1
1
1
3
3
我发现:当一个数是给定质数的倍数时,它们的最大公因数是( );当一个数不是给定质数的倍数时,它们的最大公因数是( );一个数与质数的最大公因数只有( )种情况。
质数本身
1
两
课堂小结
同学们,这节课你们学会了哪些知识?
公因数和最大公因数
几个数公有的因数,叫做这几个数的公因数;其中最大的一个公因数,叫做这几个数的最大公因数。
求两个数的最大公因数,常用的方法有:列举法、筛选法、分解质因数法和短除法。
4 分数的意义和性质
4.约分
数学人教版五年级下册
第2课时 分数与除法
新知探究
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用一种边长整分米数的正方形地砖将储藏室的地面铺满(用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
阅读与理解
16 dm
12 dm
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块)
整块正方形地砖正好铺满
可以选择边长是几分米的地砖?边长最大是几分米?
dm
边长最大是几分米?
地面长16 dm,宽12 dm。
用边长 1 dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
可以画图来探究。
16 dm
12 dm
长边:16÷1=16(块)
1 dm
1 dm
宽边:12÷1=12(块)
分析与解答
用边长 2 dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
16 dm
12 dm
长边:16÷2=8(块)
2 dm
2dm
宽边:12÷2=6(块)
分析与解答
用边长 3dm 的地砖铺,长边上用上了整数块吗?宽边上呢?
16 dm
12 dm
长边:16÷3=5(块)……1
宽边:12÷3=4(块)
分析与解答
3dm
3dm
分析与解答
要使所用的地砖都是整块的,地砖的边长必须是12和16的公因数。
想一想:为什么边长是1dm、2dm的正方形地砖能铺满贮藏室地面,而边长是3dm的正方形地砖不能呢?
因为1、2是12和16的公因数,而3是12的因数,不是16的因数。
只要找出16和12的公因数和最大公因数,就能求出正方形地砖的边长以及最大边长是多少。
分析与解答
16的因数有:1, 2, 4, 8, 16
12的因数有:1, 2, 3, 4, 6, 12
12和16的公因数有:1, 2, 4。最大公因数是4。
所以,可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用边长是整分米数的正方形地砖将储藏室的地面铺满(使用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
12和16的公因数有:1, 2, 4。最大公因数是4。
答:可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
规范解答
回顾小结
在铺地砖问题中,要使地面铺满且使用的地砖都是整块,就是求长和宽的公因数;求地砖的边长最大是多少,就是求长和宽的最大公因数。
当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
课堂练习
(教材第63页第5题)
正方形的边长必须是70和50的公因数。
就是求70和50的最大公因数。
70的因数有:1,2 ,5 ,7 ,10,14, 35,70
50的因数有:1,2, 5,10,25,50
70和50的公因数有1,2,5,10,最大公因数是10。
答:剪出的正方形的边长最大是10厘米。
1. 有一张长方形纸,长70cm,宽50cm。如果要剪成若干张同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?
(2)两个连续自然数的和是23,这两个数的最大公因数是( )。
(1)5和7的最大公因数是( )。
2. 填一填。
(3)如果a=5b(且b>5),那么a与b的最大公因数是( )。
1
1
b
(4)1和任意非零自然数的最大公因数是( )。
1
(2) 24是48和96的( )。
A.因数 B.公因数 C.最大公因数
(1)既有公因数2又有公因数3的一组数是( )。
A.30和12 B.16和25 C.14和15
3. 选一选。
(3)甲数和乙数是两个连续的自然数(甲、乙都不为0),它们的最大公因数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
B
A
每排人数必须是48和36的公因数。
就是求48和36的最大公因数。
思路引导
先求出每排最多有多少人,再分别算出男、女生有几排。
4. 男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
规范解答
36
48
2
2
18
24
9
12
3
3
4
36和48的最大公因数是2×2×3=12。
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男生有4排,女生有3排。
4. 男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
16的因数有:1,2 ,4 ,8 ,16
12的因数有:1,2 ,3 ,4 ,6, 12
1.要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米?
12 cm
16 cm
44 cm
每段木棒的长度必须是12、16和44的公因数。
就是求12、16和44的最大公因数。
44的因数有:1,2 ,4 ,11,22, 44
12、16和44的公因数有:1,2 ,4,最大公因数是4。
答:每段最长是 4 厘米。
提升练习
(教材第64页第11*题)
2 . 把46块水果糖和38块巧克力分别平均分给几个小朋友。结果水果糖剩1块,巧克力剩3块,你知道最多有多少个小朋友吗?
思路引导
46块水果糖平均分给小朋友后,剩1块。
45块水果糖可以正好分完。
38块巧克力平均分给小朋友后,剩3块。
35块巧克力可以正好分完。
求小朋友最多有多少个,就是求45和35的最大公因数。
2 . 把46块水果糖和38块巧克力分别平均分给几个小朋友。结果水果糖剩1块,巧克力剩3块,你知道最多有多少个小朋友吗?
规范解答
46-1=45(块)
38-3=35(块)
45
35
5
9
7
45和35的最大公因数是5,即最多有5个小朋友。
答:最多有5个小朋友。
课堂小结
同学们,这节课你们学会了哪些知识?
公因数和最大公因数的应用
在铺地砖问题中,要使地面铺满且使用的地砖是整块时,就是求长和宽的公因数;要求地砖的边长最大是多少,就是求长和宽的最大公因数。
4 分数的意义和性质
4.约分
数学人教版五年级下册
第3课时 分数与除法
1. 理解约分和最简分数的意义,进一步加深对分数的基本性质、公因数、最大公因数的认识。探究并掌握约分的方法,能灵活运用所学知识正确约分。
2. 在活动中提升学生的观察操作能力、归纳概括能力。
3. 积累数学活动经验,体验数学学习的乐趣。
学习目标
【重点】
归纳、概括出最简分数的概念及约分的方法。
【难点】
理解约分的意义,掌握约分的方法。
课堂导入
在括号里填上适当的数。
32
20
( )
8
=
9
6
( )
3
=
5
2
24
18
( )
3
=
4
这是根据什么?
分数的基本性质:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
÷4
÷4
÷3
÷3
÷6
÷6
把下面各分数中分子和分母的最大公因数填在括号里。
8
7
( )
36
24
( )
20
15
( )
26
13
( )
1
12
5
13
新知探究
(教材第65页例4)
把 化成分子和分母比较小且分数大小不变的分数。
30
24
你是怎么考虑的?
利用分数的基本性质。
30
24
=
30÷2
24÷2
=
15
12
方法一
用分子和分母的公因数( 1 除外)去除。
15
12
=
15÷3
12÷3
=
5
4
把 化成分子和分母比较小且分数大小不变的分数。
30
24
=
30÷2
24÷2
=
15
12
方法一
用分子和分母的公因数( 1 除外)去除。
15
12
=
15÷3
12÷3
=
5
4
30
24
想一想:有没有更简便的方法?
方法二
用分子和分母的最大公因数去除。
30
24
=
30÷6
24÷6
=
5
4
30
24
15
12
5
4
=
变小
变小
变小
变小
=
像这样,把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。
同样是约分,把 约成 和 有什么不同?
30
24
15
12
5
4
15
12
5
4
分子分母的公因数还有3,还能继续除。
分子分母的公因数只有1,不能继续除。
的分子和分母只有公因数 1 , 像这样的分数叫作最简分数。
5
4
约分时,通常要约成最简分数。
30
24
=
30÷2
24÷2
=
15
12
15
12
=
15÷3
12÷3
=
5
4
30
24
=
30÷6
24÷6
=
5
4
约分时也可以这样写:
30
24
12
15
4
5
=
5
4
÷2
÷3
30
24
4
5
=
5
4
÷6
逐次约分法
一次约分法
回顾小结
与原来的分数相比,约分后的分数大小不变,但分子、分母都变小了。
约分时,每次都要用分子、分母的公因数或最大公因数去除。通常要约成分子和分母只有公因数1(互质)的最简分数。
课堂练习
(教材第65页“做一做”)
1. 下列分数中哪些是最简分数?把不是最简分数的化成最简分数。
16
15
21
10
30
17
45
20
91
31
18
4
11
6
48
12
15
9
45
20
4
9
=
9
4
÷5
18
4
2
9
=
9
2
÷2
48
12
1
4
=
4
1
÷12
15
9
3
5
=
5
3
÷3
2. 把上下两行相等的两个分数用线连起来。
7
3
6
4
5
2
8
6
9
3
21
9
4
3
3
1
25
10
3
2
(教材第65页“做一做”)
(2)分数 的分子和分母的最大公因数是( ) ,化成最简分数是( )。
(1)一个分数约分后,分数的大小( )。
3. 填一填。
(3)分母是 8 的最简真分数的和是( )。
不变
3
2
(4)一个最简真分数,分子和分母的积是7,这个分数是( )。
27
6
9
2
7
1
4. 在 里填上“>”“<”或“=”。
32
8
4
3
9
6
3
1
5
3
10
8
7
5
21
15
25
5
5
1
8
3
24
21
1
4
<
2
3
<
4
5
>
5
7
=
1
5
=
7
8
<
5. 在括号里填上最简分数。
8分米=( )米
450千克=( )吨
250毫升=( )升
150平方分米=( )平方米
35秒=( )分
2800平方米=( )公顷
8÷10=
8
10
4
5
=
5
4
450÷1000=
450
1000
9
20
=
20
9
250÷1000=
250
1000
1
4
=
4
1
2800÷10000=
2800
10000
7
25
=
25
7
150÷100=
150
100
3
2
=
2
3
35÷60=
35
60
7
12
=
12
7
(教材第66页第5题)
6. 兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
标准量。
80张
照片总数
喜欢的35张
占几分之几
其他的
占几分之几
思路引导
求一个数是另一个数的几分之几,用除法。分别表示出喜欢的照片和其他的照片各占总数的几分之几,再约分化简。
6. 兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
80张
照片总数
喜欢的35张
占几分之几
其他的
占几分之几
规范解答
35÷80 =
80
35
7
16
=
16
7
(80-35)÷80 =
80
45
9
16
=
16
9
答: 兰兰喜欢的照片和其他的照片分别占照片总数的 和 。
16
9
16
7
(教材第66页第5题)
提升练习
1. 化简一个分数时,用2约了两次,用3约了一次,得
。求原来的分数。
本题可用倒推法求解。
(教材第67页第13*题)
8
3
思路引导
( )÷2÷2÷3
( )÷2÷2÷3
=
8
3
÷2
÷2
÷2
÷2
÷3
÷3
×3
×3
×2
×2
×2
×2
8
3
24
9
=
48
18
96
36
=
×3
×3
=
×2
×2
×2
×2
提升练习
1. 化简一个分数时,用2约了两次,用3约了一次,得
。求原来的分数。
8
3
规范解答
3×3×2×2
8×3×2×2
=
96
36
答:原来的分数是 。
96
36
(教材第67页第13*题)
2 . 把 约成最简分数。
思路引导
分子、分母的最大公因数是100010001
分子、分母同时除以100010001就可得到最简分数。
202020202020
202120212021
202020202020
202120212021
分子202020202020=2020×100010001
分母202120212021=2021×100010001
规范解答
=
2020×100010001
2021×100010001
=
2021
2020
课堂小结
同学们,这节课你们学会了哪些知识?
约分
把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。分子和分母只有公因数1的分数,叫作最简分数。
Thank you!
