3 图形的运动(一)(课件)-数学人教版二年级下册(共94张PPT)
文档属性
| 名称 | 3 图形的运动(一)(课件)-数学人教版二年级下册(共94张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 23.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 20:04:17 | ||
图片预览






文档简介
(共94张PPT)
3 图形的运动(一)
第1课时 对称现象和轴对称图形
数学人教版二年级下册
学习目标
1.通过观察、操作、想象初步认识对称现象能举例说出生活中的对称现象。
2.通过观察和操作,结合实例说出什么是轴对称图形,能够指出它们的对称轴。
3.经历得到轴对称图形的过程,会判断一个图形是不是轴对称图形,发展空间观念。
【重点】
认识轴对称图形对折后完全重合的特征。
【难点】
准确判断一个图形是否是轴对称
图形。
探究新知
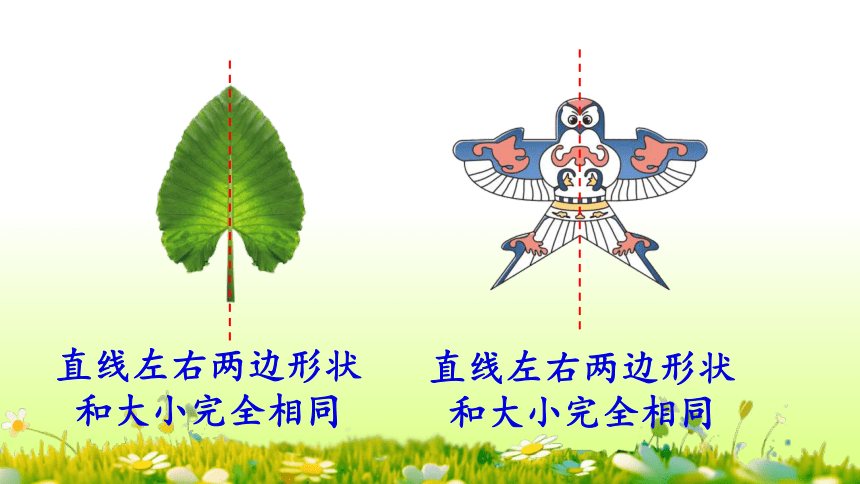
观察这些物体,它们有什么共同的特点?
直线左右两边形状和大小完全相同
直线左右两边形状和大小完全相同
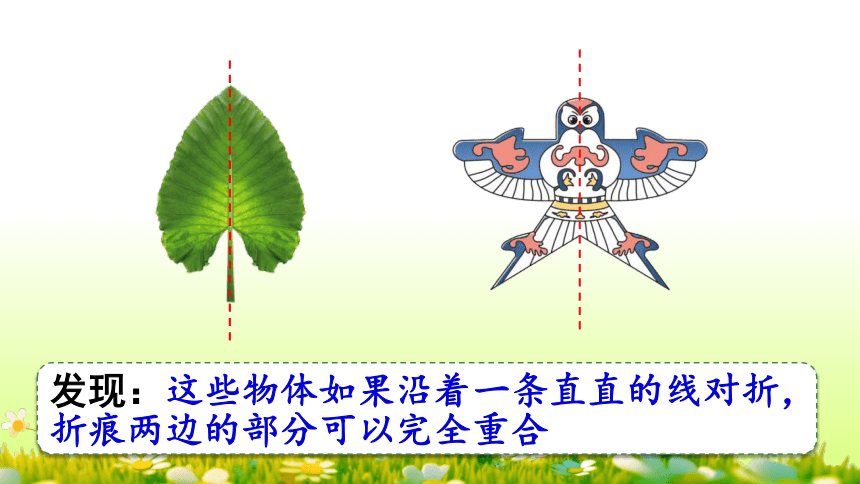
发现:这些物体如果沿着一条直直的线对折,折痕两边的部分可以完全重合
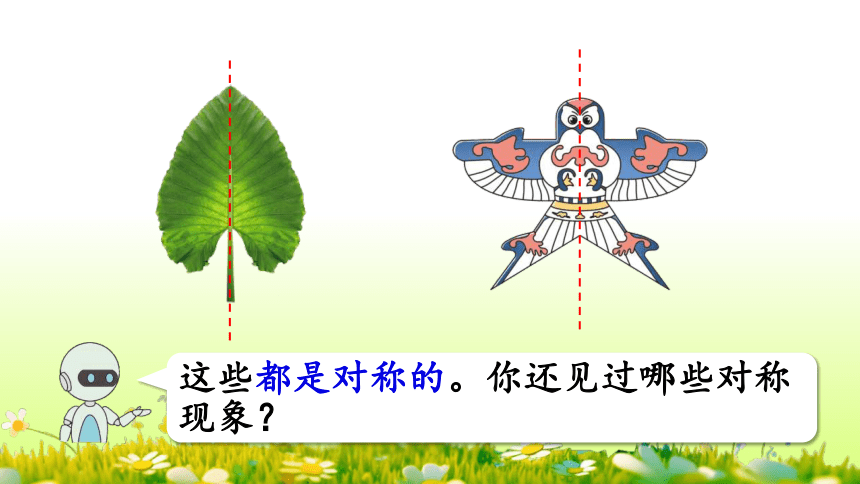
这些都是对称的。你还见过哪些对称现象?
窗花
脸谱
田字格
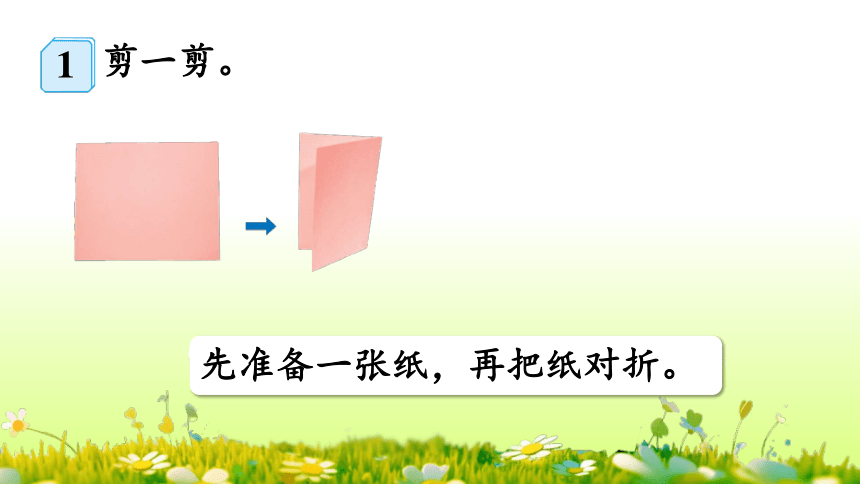
剪一剪。
先准备一张纸,再把纸对折。
1
在对折的纸上画线,再沿着画的线剪一剪。
1
剪一剪。
把图形展开,中间有一道折痕。
1
剪一剪。
试一试,看看你能得到什么图形。
1
剪一剪。
像这样剪出来的图形都是对称的,它们都是轴对称图形。
对折时,折痕所在的直直的线是它的对称轴。
对称轴
对称轴
对称轴
对称轴
怎么判断一个图形是不是轴对称图形?
一个图形如果沿某条直直的线对折,对折后折痕两侧的部分能够完全重合,那么这个图形就是轴对称图形。
回忆剪轴对称图形的过程,说一说为什么要对折纸?
为了使剪出来的图形两边完全一样。
为什么只在一边画图?
对折了。虽然只在一边画,但两边是一样的。
教材第29页“做一做”
下面哪些图形是轴对称图形?在( )里画“√”。
沿某条直直的线对折,对折后折痕两侧的部分能够完全重合。
( )
( )
( )
教材第29页“做一做”
下面哪些图形是轴对称图形?在( )里画“√”。
( )
( )
( )
√
√
课堂练习
中
D
√
√
√
×
下面这些图形中,哪些是轴对称图形?指出 它们的对称轴。
1.
下面的图形分别是从哪张纸上剪下来的?连一连。
2.
课堂小结
这节课你有什么收获?
物体左右两部分大小和形状完全相同,对折后能够完全重合,这种现象叫对称现象。
把一个图形沿着一条直线对折,对折后折痕两侧的部分能够完全重合,这样的图形就是轴对称图形。折痕所在的直线叫它的对称轴。
对称轴
对称轴
对称轴
3 图形的运动(一)
第2课时 认识平移
数学人教版二年级下册
学习目标
1.通过观察、模仿生活中的运动实例,初步感受平移现象。
2.在观察和操作活动中,直观认识物体的平移,能辨认简单图形平移后的图形。
3.通过移一移、画一画、想一想等活动,进一步巩固对平移的认识,发展空间观念。
【重点】
认识平移现象。
【难点】
能正确辨认平移后的图形。
课堂导入
游乐场中的缆车是怎样运动的?
游乐场中的缆车是怎样运动的?
在游乐场中,你还能找到一些做类似的运动的物体吗?
探究新知
它们的运动有什么共同特点?
都沿着直的线路移动。
移动过程中,物体的位置发生了变化,物体的大小、形状和自身的方向都没有改变。
这些都是平移现象。你还见过哪些平移现象?
行驶的汽车
自动门的开关
开关抽屉
行礼箱在传送带上运动
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
①
②
④
③
⑤
⑥
先平移①号小房子试一试。
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
移一移。哪几座小房子可以通过平移相互重合?
2
这五座小房子可以通过平移互相重合。
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
平移时,它们的方向没有变化,只是位置发生了变化。
还有能够通过平移互相重合的小房子吗?
①
②
④
③
⑤
⑥
①
②
④
③
⑤
⑥
剩余这座小房子方向与其它的不同,是不能通过平移相互重合的。
还有能够通过平移互相重合的小房子吗?
①
②
④
③
⑤
⑥
这两座小房子和①⑥的方向相同,能够通过平移和它们互相重合吗?
它们大小不同,不能通过平移互相重合。
这两座小房子和①⑥的方向相同,能够通过平移和它们互相重合吗?
①
②
④
③
⑤
⑥
通过学习,你对平移有怎样的认识?
平移是物体沿直的路线移动,可以是上下、左右、斜着移动。
平移过程中物体的形状、大小、方向不变,只是位置发生了改变。
怎样画出一排小汽车?要注意什么?
1.用下面的学具画一排小汽车。
课堂练习
可以将小汽车卡片放在这辆小汽车上,通过一次次平移画出一排小汽车。
1.用下面的学具画一排小汽车。
注意小汽车的大小和方向不变。
1.用下面的学具画一排小汽车。
2.下面哪架飞机通过平移可以与右侧飞机重合?把它圈出来。
可以根据平移的特点判断:平移后物体的大小、形状、方向不变。
2.下面哪架飞机通过平移可以与右侧飞机重合?把它圈出来。
拓展提升
观看游戏,说一说 是怎样平移的?
先向( )平移,再向( )平移,再向( )平移。
下
右
下
1.物体沿直的路线移动的现象就是平移。物
体平移时可以是上下、左右、斜着移动。
2.平移时物体的形状、大小、方向不变,只
是位置发生了改变。
课堂小结
这节课你有什么收获?
3 图形的运动(一)
第3课时 认识旋转
数学人教版二年级下册
学习目标
1.通过观察生活中的旋转运动,初步感受旋转现象。
2.通过观察和对比,直观认识物体的旋转,能辨认物体的运动是平移还是旋转。
3.通过说一说、找一找、做一做等活动,进一步巩固对旋转的认识,发展空间观念。
【重点】
认识旋转现象。
【难点】
能正确区分旋转和平移运动。
新课导入
下面的娱乐设施你们都玩过吗?
你知道这个娱乐设施是怎样运动的吗?
探究新知
它们的运动是平移吗?边模仿,边说一说它们的运动有什么特点?
3
风车绕着它的中心轴转动。
转轮绕着它的中心轴转动。
转盘绕着它的中心轴转动。
它们都在绕着一个点(或一条轴)做圆周运动。
它们的共同点是什么?
像上面的物体一样,物体绕着一个点或一条轴做圆周运动,就是旋转现象。
这些都是旋转现象。你还见过哪些旋转现象?
旋转门
钟表上的指针
电力风车的扇叶
摩天轮
齿轮的转动
大摆锤
教材第31页“做一做”
陀螺旋转以后,每个点转出什么形状?试一试吧!
课堂练习
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果圆形纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果正方形纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果这张纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
不管什么形状的纸,只要绕中心做圆周运动,每个点转出的都会是圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
距离中心越远,转出的圆越大;
距离中心越近,转出的圆越小。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
课堂练习
仔细观察,如果手表方向、大小没有发生改变,只是位置发生了改变,才是平移。
1.观察下图,判断每次发生了怎样的变化,在
括号里填上“平移”或“旋转”。
( )
( )
( )
平移
旋转
旋转
○
□
○
2.下面现象中,是平移的画“□”, 是旋转的画“○”。
□
生活中的数学
拓展提升
剪纸是我国一种历史悠久的民间艺术,下面这些剪纸图案是对称的。
利用平移的知识也可以设计美丽的图案。
利用旋转的知识也可以设计美丽的图案。
你能利用学过的轴对称、平移、旋转的知识设计美丽的图案吗?试一试。
课堂小结
这节课你有什么收获?
物体绕着一个点或一条轴做圆周运动,就是旋转现象。
旋转的特征:
变
本身的方向、位置发生改变
不变
大小、形状没有改变
3 图形的运动(一)
第4课时 利用图形的运动解决问题
数学人教版二年级下册
学习目标
1.通过观察剪纸作品,感受图形中蕴含的对称、平移等知识,进一步巩固本单元知识。
2.在探索如何剪出拉手纸人的活动中,综合运用知识,化繁为简思考解决问题,感受对折次数和图形个数之间的关系。
3.通过解决实际问题,发展空间观念。
【重点】
正确剪出符合要求的剪纸作品。
【难点】
感受对折次数和图形个数之间的
关系。
可以利用我们学过的对称知识创作。
课堂导入
下面的剪纸作品是怎么做出来的?
探究新知
知道了什么?
你能剪出下边这样手拉手的2个纸人吗?
每个小人都是轴对称图形。
要剪出2个形状、大小完全相同的纸人,还不能剪断。
4
我先剪1个纸人试试。
应该怎么做?
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
再试试剪2个纸人。
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
你能剪出下边这样手拉手的2个纸人吗?
4
再试试剪2个纸人。
应该怎么做?
我是这样做的。咦?剪出来的怎么出现半个纸人了?
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
应该把纸人的中线画在有折痕的一边。
你能剪出下边这样手拉手的2个纸人吗?
4
我是这样做的。咦?剪出来的怎么出现半个纸人了?
应该怎么做?
画的时候要认真观察和思考:怎样既不剪出半个纸人,还能让剪出的纸人手拉手。
你能剪出下边这样手拉手的2个纸人吗?
4
成功了吗?
我是这样折纸的,成功了。
我是这样折纸的,也成功了。
4
你能剪出下边这样手拉手的2个纸人吗?
应该怎么做?
对折两次可以剪出两个纸人,如果再对折一次就可以剪出4个纸人了。
你能剪出4个手拉手的纸人吗 试试看吧!
画和剪要注意什么?
沿着都是对折边的部分画。
对折的地方不要剪断,因为那是纸人连
接的地方。
对折1次
对折3次
……
对折2次
对比对折纸的次数和剪出的纸人的个数。你有什么发现?
对折1次
对折3次
……
对折2次
每多对折1次,就能剪出上次的两组那么多纸人。
课堂小结
这节课你有什么收获?
根据轴对称图形的特点,在折好的纸上画出图形的一半,就能剪出多个一模一样的图形。
Thank you!
3 图形的运动(一)
第1课时 对称现象和轴对称图形
数学人教版二年级下册
学习目标
1.通过观察、操作、想象初步认识对称现象能举例说出生活中的对称现象。
2.通过观察和操作,结合实例说出什么是轴对称图形,能够指出它们的对称轴。
3.经历得到轴对称图形的过程,会判断一个图形是不是轴对称图形,发展空间观念。
【重点】
认识轴对称图形对折后完全重合的特征。
【难点】
准确判断一个图形是否是轴对称
图形。
探究新知
观察这些物体,它们有什么共同的特点?
直线左右两边形状和大小完全相同
直线左右两边形状和大小完全相同
发现:这些物体如果沿着一条直直的线对折,折痕两边的部分可以完全重合
这些都是对称的。你还见过哪些对称现象?
窗花
脸谱
田字格
剪一剪。
先准备一张纸,再把纸对折。
1
在对折的纸上画线,再沿着画的线剪一剪。
1
剪一剪。
把图形展开,中间有一道折痕。
1
剪一剪。
试一试,看看你能得到什么图形。
1
剪一剪。
像这样剪出来的图形都是对称的,它们都是轴对称图形。
对折时,折痕所在的直直的线是它的对称轴。
对称轴
对称轴
对称轴
对称轴
怎么判断一个图形是不是轴对称图形?
一个图形如果沿某条直直的线对折,对折后折痕两侧的部分能够完全重合,那么这个图形就是轴对称图形。
回忆剪轴对称图形的过程,说一说为什么要对折纸?
为了使剪出来的图形两边完全一样。
为什么只在一边画图?
对折了。虽然只在一边画,但两边是一样的。
教材第29页“做一做”
下面哪些图形是轴对称图形?在( )里画“√”。
沿某条直直的线对折,对折后折痕两侧的部分能够完全重合。
( )
( )
( )
教材第29页“做一做”
下面哪些图形是轴对称图形?在( )里画“√”。
( )
( )
( )
√
√
课堂练习
中
D
√
√
√
×
下面这些图形中,哪些是轴对称图形?指出 它们的对称轴。
1.
下面的图形分别是从哪张纸上剪下来的?连一连。
2.
课堂小结
这节课你有什么收获?
物体左右两部分大小和形状完全相同,对折后能够完全重合,这种现象叫对称现象。
把一个图形沿着一条直线对折,对折后折痕两侧的部分能够完全重合,这样的图形就是轴对称图形。折痕所在的直线叫它的对称轴。
对称轴
对称轴
对称轴
3 图形的运动(一)
第2课时 认识平移
数学人教版二年级下册
学习目标
1.通过观察、模仿生活中的运动实例,初步感受平移现象。
2.在观察和操作活动中,直观认识物体的平移,能辨认简单图形平移后的图形。
3.通过移一移、画一画、想一想等活动,进一步巩固对平移的认识,发展空间观念。
【重点】
认识平移现象。
【难点】
能正确辨认平移后的图形。
课堂导入
游乐场中的缆车是怎样运动的?
游乐场中的缆车是怎样运动的?
在游乐场中,你还能找到一些做类似的运动的物体吗?
探究新知
它们的运动有什么共同特点?
都沿着直的线路移动。
移动过程中,物体的位置发生了变化,物体的大小、形状和自身的方向都没有改变。
这些都是平移现象。你还见过哪些平移现象?
行驶的汽车
自动门的开关
开关抽屉
行礼箱在传送带上运动
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
①
②
④
③
⑤
⑥
先平移①号小房子试一试。
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
移一移。哪几座小房子可以通过平移相互重合?
2
这五座小房子可以通过平移互相重合。
移一移。哪几座小房子可以通过平移相互重合?
2
①
②
④
③
⑤
⑥
平移时,它们的方向没有变化,只是位置发生了变化。
还有能够通过平移互相重合的小房子吗?
①
②
④
③
⑤
⑥
①
②
④
③
⑤
⑥
剩余这座小房子方向与其它的不同,是不能通过平移相互重合的。
还有能够通过平移互相重合的小房子吗?
①
②
④
③
⑤
⑥
这两座小房子和①⑥的方向相同,能够通过平移和它们互相重合吗?
它们大小不同,不能通过平移互相重合。
这两座小房子和①⑥的方向相同,能够通过平移和它们互相重合吗?
①
②
④
③
⑤
⑥
通过学习,你对平移有怎样的认识?
平移是物体沿直的路线移动,可以是上下、左右、斜着移动。
平移过程中物体的形状、大小、方向不变,只是位置发生了改变。
怎样画出一排小汽车?要注意什么?
1.用下面的学具画一排小汽车。
课堂练习
可以将小汽车卡片放在这辆小汽车上,通过一次次平移画出一排小汽车。
1.用下面的学具画一排小汽车。
注意小汽车的大小和方向不变。
1.用下面的学具画一排小汽车。
2.下面哪架飞机通过平移可以与右侧飞机重合?把它圈出来。
可以根据平移的特点判断:平移后物体的大小、形状、方向不变。
2.下面哪架飞机通过平移可以与右侧飞机重合?把它圈出来。
拓展提升
观看游戏,说一说 是怎样平移的?
先向( )平移,再向( )平移,再向( )平移。
下
右
下
1.物体沿直的路线移动的现象就是平移。物
体平移时可以是上下、左右、斜着移动。
2.平移时物体的形状、大小、方向不变,只
是位置发生了改变。
课堂小结
这节课你有什么收获?
3 图形的运动(一)
第3课时 认识旋转
数学人教版二年级下册
学习目标
1.通过观察生活中的旋转运动,初步感受旋转现象。
2.通过观察和对比,直观认识物体的旋转,能辨认物体的运动是平移还是旋转。
3.通过说一说、找一找、做一做等活动,进一步巩固对旋转的认识,发展空间观念。
【重点】
认识旋转现象。
【难点】
能正确区分旋转和平移运动。
新课导入
下面的娱乐设施你们都玩过吗?
你知道这个娱乐设施是怎样运动的吗?
探究新知
它们的运动是平移吗?边模仿,边说一说它们的运动有什么特点?
3
风车绕着它的中心轴转动。
转轮绕着它的中心轴转动。
转盘绕着它的中心轴转动。
它们都在绕着一个点(或一条轴)做圆周运动。
它们的共同点是什么?
像上面的物体一样,物体绕着一个点或一条轴做圆周运动,就是旋转现象。
这些都是旋转现象。你还见过哪些旋转现象?
旋转门
钟表上的指针
电力风车的扇叶
摩天轮
齿轮的转动
大摆锤
教材第31页“做一做”
陀螺旋转以后,每个点转出什么形状?试一试吧!
课堂练习
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果圆形纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果正方形纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
如果这张纸转动,陀螺上的各点都将绕着中心点转动,最后会形成圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
不管什么形状的纸,只要绕中心做圆周运动,每个点转出的都会是圆形。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
教材第31页“做一做”
距离中心越远,转出的圆越大;
距离中心越近,转出的圆越小。
剪下教材第119页中的学具,贴在硬纸板上,照样子做陀螺。
课堂练习
仔细观察,如果手表方向、大小没有发生改变,只是位置发生了改变,才是平移。
1.观察下图,判断每次发生了怎样的变化,在
括号里填上“平移”或“旋转”。
( )
( )
( )
平移
旋转
旋转
○
□
○
2.下面现象中,是平移的画“□”, 是旋转的画“○”。
□
生活中的数学
拓展提升
剪纸是我国一种历史悠久的民间艺术,下面这些剪纸图案是对称的。
利用平移的知识也可以设计美丽的图案。
利用旋转的知识也可以设计美丽的图案。
你能利用学过的轴对称、平移、旋转的知识设计美丽的图案吗?试一试。
课堂小结
这节课你有什么收获?
物体绕着一个点或一条轴做圆周运动,就是旋转现象。
旋转的特征:
变
本身的方向、位置发生改变
不变
大小、形状没有改变
3 图形的运动(一)
第4课时 利用图形的运动解决问题
数学人教版二年级下册
学习目标
1.通过观察剪纸作品,感受图形中蕴含的对称、平移等知识,进一步巩固本单元知识。
2.在探索如何剪出拉手纸人的活动中,综合运用知识,化繁为简思考解决问题,感受对折次数和图形个数之间的关系。
3.通过解决实际问题,发展空间观念。
【重点】
正确剪出符合要求的剪纸作品。
【难点】
感受对折次数和图形个数之间的
关系。
可以利用我们学过的对称知识创作。
课堂导入
下面的剪纸作品是怎么做出来的?
探究新知
知道了什么?
你能剪出下边这样手拉手的2个纸人吗?
每个小人都是轴对称图形。
要剪出2个形状、大小完全相同的纸人,还不能剪断。
4
我先剪1个纸人试试。
应该怎么做?
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
再试试剪2个纸人。
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
你能剪出下边这样手拉手的2个纸人吗?
4
再试试剪2个纸人。
应该怎么做?
我是这样做的。咦?剪出来的怎么出现半个纸人了?
你能剪出下边这样手拉手的2个纸人吗?
4
应该怎么做?
应该把纸人的中线画在有折痕的一边。
你能剪出下边这样手拉手的2个纸人吗?
4
我是这样做的。咦?剪出来的怎么出现半个纸人了?
应该怎么做?
画的时候要认真观察和思考:怎样既不剪出半个纸人,还能让剪出的纸人手拉手。
你能剪出下边这样手拉手的2个纸人吗?
4
成功了吗?
我是这样折纸的,成功了。
我是这样折纸的,也成功了。
4
你能剪出下边这样手拉手的2个纸人吗?
应该怎么做?
对折两次可以剪出两个纸人,如果再对折一次就可以剪出4个纸人了。
你能剪出4个手拉手的纸人吗 试试看吧!
画和剪要注意什么?
沿着都是对折边的部分画。
对折的地方不要剪断,因为那是纸人连
接的地方。
对折1次
对折3次
……
对折2次
对比对折纸的次数和剪出的纸人的个数。你有什么发现?
对折1次
对折3次
……
对折2次
每多对折1次,就能剪出上次的两组那么多纸人。
课堂小结
这节课你有什么收获?
根据轴对称图形的特点,在折好的纸上画出图形的一半,就能剪出多个一模一样的图形。
Thank you!
