第八章 成对数据的统计分析 章节练习卷3(含解析)-2023-2024学年高二数学-(人教A版2019选择性必修三)
文档属性
| 名称 | 第八章 成对数据的统计分析 章节练习卷3(含解析)-2023-2024学年高二数学-(人教A版2019选择性必修三) |
|
|
| 格式 | docx | ||
| 文件大小 | 728.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 00:00:00 | ||
图片预览





文档简介
第八章成对数据的统计分析章节练习卷3-2023-2024学年高二数学-(人教A版2019选择性必必修三)
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
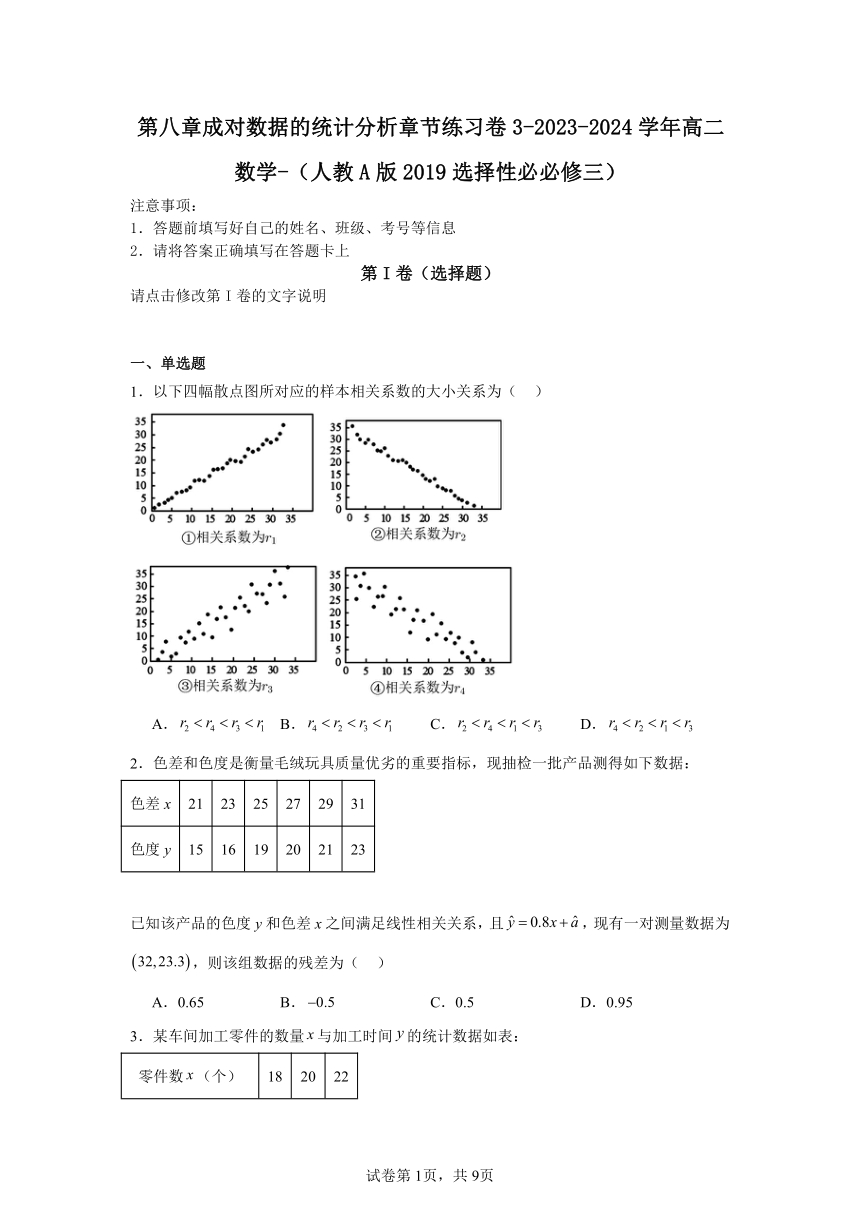
1.以下四幅散点图所对应的样本相关系数的大小关系为( )
A. B. C. D.
2.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得如下数据:
色差x 21 23 25 27 29 31
色度y 15 16 19 20 21 23
已知该产品的色度y和色差x之间满足线性相关关系,且,现有一对测量数据为,则该组数据的残差为( )
A.0.65 B. C.0.5 D.0.95
3.某车间加工零件的数量与加工时间的统计数据如表:
零件数(个) 18 20 22
加工时间(分) 27 33
现已求得上表数据的回归方程中的值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为102分钟,则的值为( )
A.28 B.29 C.30 D.32
4.部门所属的10个工业企业生产性固定资产价值与工业增加值数据如下(单位:百万元):
固定资产价值 3 3 5 6 6 7 8 9 9 10
工业增加值 15 17 25 28 30 36 37 42 40 45
根据上表数据计算的相关系数为( )
A.0 B.-0.8973 C.1.0228 D.0.9918
5.某研究所为了研究近几年中国留学生回国人数的情况,对2014至2018年留学生回国人数进行了统计,数据如下表:
年份 2014 2015 2016 2017 2018
年份代码 1 2 3 4 5
留学生回国人数/万 36.5 40.9 43.3 48.1 51.9
根据上述统计数据求得留学生回国人数(单位:万)与年份代码满足的线性回归方程为,利用回归方程预测年留学生回国人数为( )
A.63.14万 B.64.72万 C.66.81万 D.66.94万
6.用模型拟合一组数,若,,设,得变换后的线性回归方程为,则( )
A.12 B. C. D.7
7.通过随机询问相同数量的不同性别大学生在购买食物时是否看营养说明,得知有的男大学生“不看”,有的女大学生“不看”,若有99%的把握认为性别与是否看营养说明之间有关,则调查的总人数可能为( )
A.150 B.170 C.240 D.175
8.某大学为了解喜欢看篮球赛是否与性别有关,随机调查了部分学生,在被调查的学生中,男生人数是女生人数的2倍,男生喜欢看篮球赛的人数占男生人数的,女生喜欢看篮球赛的人数占女生人数的.若被调查的男生人数为,且有95%的把握认为喜欢看篮球赛与性别有关,则的最小值为( )
A.6 B.12 C.18 D.36
二、多选题
9.已知一组样本点,其中,根据最小二乘法求得的经验回归方程是,则下列说法不正确的是( ).
A.若所有样本点都在上,则变量间的样本相关系数为1
B.至少有一个样本点落在经验回归直线上
C.对所有的,响应变量的值一定与有误差
D.若的斜率,则变量x与y正拟合相关
10.“中国最具幸福感城市调查推选活动”由新华社《瞭望东方周刊》、瞭望智库共同主办,至今已连续举办15年,累计推选出80余座幸福城市,现某城市随机选取30个人进行调查,得到他们的收入、生活成本及幸福感分数(幸福感分数为0~10分),并整理得到散点图(如图),其中x是收入与生活成本的比值,y是幸福感分数,经计算得回归方程为.根据回归方程可知( )
A.y与x成正相关
B.样本点中残差的绝对值最大是2.044
C.只要增加民众的收入就可以提高民众的幸福感
D.当收入是生活成本3倍时,预报得幸福感分数为6.044
11.针对当下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”做了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数的,若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生有可能( )
附:
A. B. C. D.
三、填空题
12.由一组样本点、、、、,根据最小二乘法求得的回归方程为,则 .
13.某公司的广告费支出与销售额(单位:万元)之间有下列对应数据:由资料显示对呈线性相关关系.
2 4 5 6 8
30 40 60 50 70
根据上表提供的数据得到回归方程中的,预测销售额为115万元时约需 万元广告费.
14.下表是某饮料专卖店一天卖出奶茶的杯数y与当天气温x(单位:)的对比表,已知表中数据计算得到y关于x的线性回归方程为,则相应于点的残差为 .
气温 5 10 15 20 25
杯数y 26 20 16 14 14
第II卷(非选择题)
请点击修改第II卷的文字说明
四、解答题
15.垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多样,且具有污染性,所以需要无害化、减量化处理.某省为调查产生的垃圾数量,采用简单随机抽样的方法抽取20个县城进行了分析,得到样本数据,其中和分别表示第i个县城的人口(单位:万人)和该县年垃圾产生总量(单位:吨),并计算得:,,,,.
(1)求这20个县年垃圾产生总量的平均值;
(2)请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合.(当时,与的相关关系较强,否则相关关系较弱.)
参考公式:相关系数.
16.我国脱贫攻坚战取得全面胜利,现行标准下农村贫困人口全部脱贫,消除了绝对贫困.某村40户贫困家庭在扶贫工作组的帮助下于2017年全面脱贫,该工作组为了了解脱贫家庭的收入,消费支出,食品支出的关系,在这些脱贫家庭中利用简单随机抽样方法抽取了8户,调查统计这8户家庭每户2019年的年收入x,消费支出y,食品支出z(单位:千元),整理数据得到下面的折线图,由数据得到下表.
家庭(i) 1 2 3 4 5 6 7 8
消费支出(y) 27 30 33 35 37 40 42 44
食品支出(z) 9 10 11 13 12 11 12 12
(1)由折线图看出,可用线性回归模型拟合y与x的关系,求y关于x的回归方程(精确到0.01),并解释的现实生活意义;
(2)恩格尔系数,是食品支出额占家庭消费支出总额的比重.通常一个家庭收入越少,家庭收入中(或总支出中)用来购买食物的比重越大;一个家庭收入越多,家庭收入中(或总支出中)用来购买食物的比重越小,所以该系数是衡量居民生活水平的有效指标.根据联合国粮农组织提出的标准,恩格尔系数在59%以上为贫困,50%~59%为温饱,40%~50%为小康,30%~40%为富裕,低于30%为最富裕.根据上述样本数据,请估计该村脱贫家庭中达到最富裕的家庭户数.
参考数据:,,,.附:回归方程中斜率和截距的最小二乘估计公式分别为:,.
17.甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别抽查了两台机床生产的产品,产品的质量情况统计如下表:
一级品 二级品 合计
甲机床 30
乙机床 40
合计 90 200
(1)请将上述列联表补充完整;
(2)能否有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员,深受广大民众的喜爱,已成为最火爆的商品,“一墩难求”.某调查机构随机抽取100人,对是否有意向购买冰墩墩进行调查,结果如下表:
年龄/岁
抽取人数 10 20 25 15 18 7 5
有意向购买的人数 10 18 22 9 10 4 2
(1)若从年龄在的被调查人群中随机选出两人进行调查,求这两人中恰有一人打算购买冰墩墩的概率;
(2)若以年龄40岁为分界线,由以上统计数据完成下面的列联表,并判断是否有的把握认为购买冰墩墩与人的年龄有关?
年龄低于40岁的人数 年龄不低于40岁的人数 总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计
参考数据:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.某县城为活跃经济,特举办传统文化民俗节,小张弄了一个套小白兔的摊位,设表示第i天的平均气温,表示第i天参与活动的人数,,根据统计,计算得到如下一些统计量的值:
,,.
(1)根据所给数据,用相关系数(精确到0.01)判断是否可用线性回归模型拟合与的关系;
(2)现有两个家庭参与套圈,A家庭3位成员每轮每人套住小白兔的概率都为,B家庭3位成员每轮每人套住小白兔的概率分别为,每个家庭的3位成员均玩一次套圈为一轮,每轮每人收费20元,每个小白兔价值40元,且每人是否套住相互独立,以每个家庭的盈利的期望为决策依据,问:一轮结束后,哪个家庭损失较大?
附:相关系数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据散点图及相关系数的概念判断即可;
【详解】解:根据散点图可知,图①③成正相关,图②④成负相关,所以,,,,
又图①②的散点图近似在一条直线上,所以图①②两变量的线性相关程度比较高,
图③④的散点图比较分散,故图③④两变量的线性相关程度比较低,即与比较大,与比较小,所以;
故选:A
2.B
【分析】求出样本中心点,代入线性回归方程,求出,进而求出残差.
【详解】由表中数据可得,,将代入经验回归方程得到,所以.将代入,可得,因此其残差为.
故选:B
3.C
【分析】根据题意求得,再结合线性回归方程过样本中心点运算求解.
【详解】由题意可知:,
且当时,,解得,
可知,
又因为,
可知点在上,
即,解得.
故选:C.
4.D
【分析】根据已知条件,结合相关系数的公式,即可求解.
【详解】由表中数据可得,,,
,,
,
故.
故选:D.
5.D
【分析】先求出样本点的中心,代入线性回归方程即可求出,再将代入线性回归方程即可得到结果.
【详解】由题意知:,,
所以样本点的中心为,所以,解得:,
可得线性回归方程为,
年对应的年份代码为,令, 则,
所以预测2022年留学生回国人数为66.94万,
故选:D.
6.B
【分析】由已知,可根据,先计算出,然后把样本中心点带入线性回归方程为中计算出,从而得到线性回归方程,然后将方程化为指数形式,通过待定系数法分别对应出、的值,即可完成求解.
【详解】由已知,,所以,
,,所以
,
由题意,满足线性回归方程为,所以,所以,
此时线性回归方程为,即,
可将此式子化为指数形式,即为,
因为模型为模型,所以,,
所以.
故选:B.
7.C
【分析】由题意列出2×2列联表,并计算出,根据有99%的把握认为性别与是否看营养说明之间有关,列出不等式,解出,可得答案.
【详解】设男女大学生各有m人,根据题意画出2×2列联表,如下图:
看 不看 合计
男 m
女 m
合计 2m
所以,因为有99%的把握认为性别与对产品是否满意有关,所以,解得,所以总人数2m可能为240.
故选:C.
8.B
【分析】列出列联表,计算,解不等式,即可求解.
【详解】由题意得到如下列联表:
喜欢看篮球赛情况 性别 喜欢 不喜欢 总计
男
女
总计
所以.
因为有95%的把握认为喜欢看篮球赛与性别有关,所以,
即,得.
又,,为整数,所以的最小值为12.
故选:B
9.ABC
【分析】根据回归方程性质对选项一一判断即可.
【详解】选项A,所有样本点都在上,则变量间的样本相关系数,样本相关系数为,故A错误;
选项B,经验回归直线必过样本中心点,但样本点可能都不在经验回归直线上,故B错误;
选项C,样本点可能在直线上,即可能存在对应的响应变量与没有误差,故C错误;
选项D,样本相关系数r与符号相同,若的斜率,则,样本点的分布从左至右上升,变量x与y正相关,故D正确.
故选:ABC
10.ABD
【分析】根据给定散点图,利用相关性的意义判断A;计算残差判断B;举例说明判断C;利用回归方程计算判断D作答.
【详解】对于A,由散点图知,当x增大时,y也增大,y与x成正相关,A正确;
对于B,由图知,点A是残差绝对值最大的点,当时,,
则残差,所以残差的绝对值最大是2.044,B正确;
对于C,若增加民众的收入,而生活成本增加的更多,收入与生活成本的比值x反而减小,幸福感分数y减小,C不正确;
对于D,收入是生活成本的3倍,即,则,幸福感分数预报值为6.044,D正确.
故选:ABD
11.BC
【分析】先设男生人数为,,列出列联表,利用独立性检验计算观测值,再结合观测值列关系即得答案.
【详解】解:由题意被调查的男女生人数相同,设男生的人数为:,,由题意可列出列联表:
男生 女生 合计
喜欢锻炼
不喜欢锻炼
合计
.
由于有的把握认为是否喜欢抖音和性别有关,
所以;
解得:,因为,
故的可能取值为:9、10、11、12、13,即男生的人数可以是45,50,55,60,65.
则选项中被调查学生中男生的人数可能45或60.
故选:BC.
12.
【分析】求出样本中心点的坐标,代入回归直线方程即可求得的值.
【详解】由已知条件可得,,
将点的坐标代入回归直线方程可得,解得.
故答案为:.
13.15
【详解】试题分析:,
∴这组数据的样本中心点是(5,50)
∵b=6.5,
∴y=6.5x+a,
把样本中心点代入得a=19.75
∴线性回归方程是y=6.5x+19.75
当y=115时,x≈15
考点:回归方程
14..
【分析】由表中数据计算出,,代入线性回归方程求出,进而可求得结果.
【详解】,,
代入线性回归方程得,解得,
则线性回归方程为.
所以,则相应于点的残差为.
故答案为:.
15.(1)
(2)理由见解析
【分析】(1)根据直接计算可得;
(2)根据所给数据计算出相关系数,即可说明.
【详解】(1)依题意这个县年垃圾产生总量的平均值为(吨).
(2)依题意,
因为与的相关系数接近,所以与之间具有较强的线性相关关系,可用线性回归模型进行拟合.
16.(1)回归方程为,的现实意义为年收入每增加1千元,估计消费支出增加0.68千元;(2)(户).
【分析】(1)分析题意,按照求回归方程的步骤求出线性回归方程,并进行估计;
(2)根据题意计算样本中达到最富裕的家庭的频率,即可估计全部家庭中达到最富裕的家庭的个数.
【详解】解:(1)由题,可知,,
所以,
故.
所以y关于x的回归方程为.
的现实意义为年收入每增加1千元,估计消费支出增加0.68千元.
(2)由题意可知,8户脱贫家庭的恩格尔系数如下表所示:
家庭(i) 1 2 3 4 5 6 7 8
恩格尔系数 33.3% 33.3% 33.3% 37.1% 32.4% 27.5% 28.6% 27.2%
所以样本中达到最富裕的家庭有3个,
估计该村脱贫家庭中达到最富裕的家庭户数为(户).
【点睛】求线性回归方程的步骤:①求出;②套公式求出;③写出回归方程;④利用回归方程进行预报;
17.(1)列联表见解析
(2)有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异
【分析】(1)直接计算补充列联表即可;
(2)先计算,再和10.828比较作出判断即可.
【详解】(1)补充完整的列联表如下:
一级品 二级品 合计
甲机床 30 70 100
乙机床 60 40 100
合计 90 110 200
(2)∵,
∴有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异.
18.(1);
(2)列联表见解析,有的把握认为购买冰墩墩与人的年龄有关.
【分析】(1)运用列举法结合古典概型运算公式进行求解即可;
(2)根据表中数据直接完成列联表,结合题中所给的公式进行计算、表中所给的数据进行判断即可.
【详解】(1)因为年龄在之间抽取的人数为7,有意向购买的人数为,
为7人编号为1,2,3,4,5,6,7,其中有意向购买的人的编号为1,2,3,4,
从7人中抽取2人的所有基本事件为:
,共21种,
其中两人中恰有一人打算购买冰墩墩的基本事件有12种,
故所求概率为:.
(2)由调查表可得:
年龄低于40岁的人数 年龄不低于40岁的人数 总计
有意向购买冰墩墩的人数 50 25 75
无意向购买冰墩墩的人数 5 20 25
总计 55 45 100
,
所以有的把握认为购买冰墩墩与人的年龄有关.
19.(1)可用线性回归模型拟合y与x的关系.
(2)B家庭的损失较大
【分析】(1)计算相关系数,若接近1,则可用线性回归模型拟合与的关系.
(2)A家庭符合二项分布,直接用公式求期望,B家庭先根据题意列出分布列再求期望.
【详解】(1)由题可知
,
故可用线性回归模型拟合y与x的关系.
(2)设A家庭中套中小白兔的人数为,则,
所以.
设A家庭的盈利为元,则,
所以.
设B家庭中套中小白兔的人数为,
则的所有可能取值为0,1,2,3,
,
,
,
,
所以.
设B家庭的盈利为元,则,
所以.
因为,所以B家庭的损失较大
答案第1页,共2页
答案第1页,共2页
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.以下四幅散点图所对应的样本相关系数的大小关系为( )
A. B. C. D.
2.色差和色度是衡量毛绒玩具质量优劣的重要指标,现抽检一批产品测得如下数据:
色差x 21 23 25 27 29 31
色度y 15 16 19 20 21 23
已知该产品的色度y和色差x之间满足线性相关关系,且,现有一对测量数据为,则该组数据的残差为( )
A.0.65 B. C.0.5 D.0.95
3.某车间加工零件的数量与加工时间的统计数据如表:
零件数(个) 18 20 22
加工时间(分) 27 33
现已求得上表数据的回归方程中的值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为102分钟,则的值为( )
A.28 B.29 C.30 D.32
4.部门所属的10个工业企业生产性固定资产价值与工业增加值数据如下(单位:百万元):
固定资产价值 3 3 5 6 6 7 8 9 9 10
工业增加值 15 17 25 28 30 36 37 42 40 45
根据上表数据计算的相关系数为( )
A.0 B.-0.8973 C.1.0228 D.0.9918
5.某研究所为了研究近几年中国留学生回国人数的情况,对2014至2018年留学生回国人数进行了统计,数据如下表:
年份 2014 2015 2016 2017 2018
年份代码 1 2 3 4 5
留学生回国人数/万 36.5 40.9 43.3 48.1 51.9
根据上述统计数据求得留学生回国人数(单位:万)与年份代码满足的线性回归方程为,利用回归方程预测年留学生回国人数为( )
A.63.14万 B.64.72万 C.66.81万 D.66.94万
6.用模型拟合一组数,若,,设,得变换后的线性回归方程为,则( )
A.12 B. C. D.7
7.通过随机询问相同数量的不同性别大学生在购买食物时是否看营养说明,得知有的男大学生“不看”,有的女大学生“不看”,若有99%的把握认为性别与是否看营养说明之间有关,则调查的总人数可能为( )
A.150 B.170 C.240 D.175
8.某大学为了解喜欢看篮球赛是否与性别有关,随机调查了部分学生,在被调查的学生中,男生人数是女生人数的2倍,男生喜欢看篮球赛的人数占男生人数的,女生喜欢看篮球赛的人数占女生人数的.若被调查的男生人数为,且有95%的把握认为喜欢看篮球赛与性别有关,则的最小值为( )
A.6 B.12 C.18 D.36
二、多选题
9.已知一组样本点,其中,根据最小二乘法求得的经验回归方程是,则下列说法不正确的是( ).
A.若所有样本点都在上,则变量间的样本相关系数为1
B.至少有一个样本点落在经验回归直线上
C.对所有的,响应变量的值一定与有误差
D.若的斜率,则变量x与y正拟合相关
10.“中国最具幸福感城市调查推选活动”由新华社《瞭望东方周刊》、瞭望智库共同主办,至今已连续举办15年,累计推选出80余座幸福城市,现某城市随机选取30个人进行调查,得到他们的收入、生活成本及幸福感分数(幸福感分数为0~10分),并整理得到散点图(如图),其中x是收入与生活成本的比值,y是幸福感分数,经计算得回归方程为.根据回归方程可知( )
A.y与x成正相关
B.样本点中残差的绝对值最大是2.044
C.只要增加民众的收入就可以提高民众的幸福感
D.当收入是生活成本3倍时,预报得幸福感分数为6.044
11.针对当下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”做了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数的,若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生有可能( )
附:
A. B. C. D.
三、填空题
12.由一组样本点、、、、,根据最小二乘法求得的回归方程为,则 .
13.某公司的广告费支出与销售额(单位:万元)之间有下列对应数据:由资料显示对呈线性相关关系.
2 4 5 6 8
30 40 60 50 70
根据上表提供的数据得到回归方程中的,预测销售额为115万元时约需 万元广告费.
14.下表是某饮料专卖店一天卖出奶茶的杯数y与当天气温x(单位:)的对比表,已知表中数据计算得到y关于x的线性回归方程为,则相应于点的残差为 .
气温 5 10 15 20 25
杯数y 26 20 16 14 14
第II卷(非选择题)
请点击修改第II卷的文字说明
四、解答题
15.垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多样,且具有污染性,所以需要无害化、减量化处理.某省为调查产生的垃圾数量,采用简单随机抽样的方法抽取20个县城进行了分析,得到样本数据,其中和分别表示第i个县城的人口(单位:万人)和该县年垃圾产生总量(单位:吨),并计算得:,,,,.
(1)求这20个县年垃圾产生总量的平均值;
(2)请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合.(当时,与的相关关系较强,否则相关关系较弱.)
参考公式:相关系数.
16.我国脱贫攻坚战取得全面胜利,现行标准下农村贫困人口全部脱贫,消除了绝对贫困.某村40户贫困家庭在扶贫工作组的帮助下于2017年全面脱贫,该工作组为了了解脱贫家庭的收入,消费支出,食品支出的关系,在这些脱贫家庭中利用简单随机抽样方法抽取了8户,调查统计这8户家庭每户2019年的年收入x,消费支出y,食品支出z(单位:千元),整理数据得到下面的折线图,由数据得到下表.
家庭(i) 1 2 3 4 5 6 7 8
消费支出(y) 27 30 33 35 37 40 42 44
食品支出(z) 9 10 11 13 12 11 12 12
(1)由折线图看出,可用线性回归模型拟合y与x的关系,求y关于x的回归方程(精确到0.01),并解释的现实生活意义;
(2)恩格尔系数,是食品支出额占家庭消费支出总额的比重.通常一个家庭收入越少,家庭收入中(或总支出中)用来购买食物的比重越大;一个家庭收入越多,家庭收入中(或总支出中)用来购买食物的比重越小,所以该系数是衡量居民生活水平的有效指标.根据联合国粮农组织提出的标准,恩格尔系数在59%以上为贫困,50%~59%为温饱,40%~50%为小康,30%~40%为富裕,低于30%为最富裕.根据上述样本数据,请估计该村脱贫家庭中达到最富裕的家庭户数.
参考数据:,,,.附:回归方程中斜率和截距的最小二乘估计公式分别为:,.
17.甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别抽查了两台机床生产的产品,产品的质量情况统计如下表:
一级品 二级品 合计
甲机床 30
乙机床 40
合计 90 200
(1)请将上述列联表补充完整;
(2)能否有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员,深受广大民众的喜爱,已成为最火爆的商品,“一墩难求”.某调查机构随机抽取100人,对是否有意向购买冰墩墩进行调查,结果如下表:
年龄/岁
抽取人数 10 20 25 15 18 7 5
有意向购买的人数 10 18 22 9 10 4 2
(1)若从年龄在的被调查人群中随机选出两人进行调查,求这两人中恰有一人打算购买冰墩墩的概率;
(2)若以年龄40岁为分界线,由以上统计数据完成下面的列联表,并判断是否有的把握认为购买冰墩墩与人的年龄有关?
年龄低于40岁的人数 年龄不低于40岁的人数 总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计
参考数据:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.某县城为活跃经济,特举办传统文化民俗节,小张弄了一个套小白兔的摊位,设表示第i天的平均气温,表示第i天参与活动的人数,,根据统计,计算得到如下一些统计量的值:
,,.
(1)根据所给数据,用相关系数(精确到0.01)判断是否可用线性回归模型拟合与的关系;
(2)现有两个家庭参与套圈,A家庭3位成员每轮每人套住小白兔的概率都为,B家庭3位成员每轮每人套住小白兔的概率分别为,每个家庭的3位成员均玩一次套圈为一轮,每轮每人收费20元,每个小白兔价值40元,且每人是否套住相互独立,以每个家庭的盈利的期望为决策依据,问:一轮结束后,哪个家庭损失较大?
附:相关系数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据散点图及相关系数的概念判断即可;
【详解】解:根据散点图可知,图①③成正相关,图②④成负相关,所以,,,,
又图①②的散点图近似在一条直线上,所以图①②两变量的线性相关程度比较高,
图③④的散点图比较分散,故图③④两变量的线性相关程度比较低,即与比较大,与比较小,所以;
故选:A
2.B
【分析】求出样本中心点,代入线性回归方程,求出,进而求出残差.
【详解】由表中数据可得,,将代入经验回归方程得到,所以.将代入,可得,因此其残差为.
故选:B
3.C
【分析】根据题意求得,再结合线性回归方程过样本中心点运算求解.
【详解】由题意可知:,
且当时,,解得,
可知,
又因为,
可知点在上,
即,解得.
故选:C.
4.D
【分析】根据已知条件,结合相关系数的公式,即可求解.
【详解】由表中数据可得,,,
,,
,
故.
故选:D.
5.D
【分析】先求出样本点的中心,代入线性回归方程即可求出,再将代入线性回归方程即可得到结果.
【详解】由题意知:,,
所以样本点的中心为,所以,解得:,
可得线性回归方程为,
年对应的年份代码为,令, 则,
所以预测2022年留学生回国人数为66.94万,
故选:D.
6.B
【分析】由已知,可根据,先计算出,然后把样本中心点带入线性回归方程为中计算出,从而得到线性回归方程,然后将方程化为指数形式,通过待定系数法分别对应出、的值,即可完成求解.
【详解】由已知,,所以,
,,所以
,
由题意,满足线性回归方程为,所以,所以,
此时线性回归方程为,即,
可将此式子化为指数形式,即为,
因为模型为模型,所以,,
所以.
故选:B.
7.C
【分析】由题意列出2×2列联表,并计算出,根据有99%的把握认为性别与是否看营养说明之间有关,列出不等式,解出,可得答案.
【详解】设男女大学生各有m人,根据题意画出2×2列联表,如下图:
看 不看 合计
男 m
女 m
合计 2m
所以,因为有99%的把握认为性别与对产品是否满意有关,所以,解得,所以总人数2m可能为240.
故选:C.
8.B
【分析】列出列联表,计算,解不等式,即可求解.
【详解】由题意得到如下列联表:
喜欢看篮球赛情况 性别 喜欢 不喜欢 总计
男
女
总计
所以.
因为有95%的把握认为喜欢看篮球赛与性别有关,所以,
即,得.
又,,为整数,所以的最小值为12.
故选:B
9.ABC
【分析】根据回归方程性质对选项一一判断即可.
【详解】选项A,所有样本点都在上,则变量间的样本相关系数,样本相关系数为,故A错误;
选项B,经验回归直线必过样本中心点,但样本点可能都不在经验回归直线上,故B错误;
选项C,样本点可能在直线上,即可能存在对应的响应变量与没有误差,故C错误;
选项D,样本相关系数r与符号相同,若的斜率,则,样本点的分布从左至右上升,变量x与y正相关,故D正确.
故选:ABC
10.ABD
【分析】根据给定散点图,利用相关性的意义判断A;计算残差判断B;举例说明判断C;利用回归方程计算判断D作答.
【详解】对于A,由散点图知,当x增大时,y也增大,y与x成正相关,A正确;
对于B,由图知,点A是残差绝对值最大的点,当时,,
则残差,所以残差的绝对值最大是2.044,B正确;
对于C,若增加民众的收入,而生活成本增加的更多,收入与生活成本的比值x反而减小,幸福感分数y减小,C不正确;
对于D,收入是生活成本的3倍,即,则,幸福感分数预报值为6.044,D正确.
故选:ABD
11.BC
【分析】先设男生人数为,,列出列联表,利用独立性检验计算观测值,再结合观测值列关系即得答案.
【详解】解:由题意被调查的男女生人数相同,设男生的人数为:,,由题意可列出列联表:
男生 女生 合计
喜欢锻炼
不喜欢锻炼
合计
.
由于有的把握认为是否喜欢抖音和性别有关,
所以;
解得:,因为,
故的可能取值为:9、10、11、12、13,即男生的人数可以是45,50,55,60,65.
则选项中被调查学生中男生的人数可能45或60.
故选:BC.
12.
【分析】求出样本中心点的坐标,代入回归直线方程即可求得的值.
【详解】由已知条件可得,,
将点的坐标代入回归直线方程可得,解得.
故答案为:.
13.15
【详解】试题分析:,
∴这组数据的样本中心点是(5,50)
∵b=6.5,
∴y=6.5x+a,
把样本中心点代入得a=19.75
∴线性回归方程是y=6.5x+19.75
当y=115时,x≈15
考点:回归方程
14..
【分析】由表中数据计算出,,代入线性回归方程求出,进而可求得结果.
【详解】,,
代入线性回归方程得,解得,
则线性回归方程为.
所以,则相应于点的残差为.
故答案为:.
15.(1)
(2)理由见解析
【分析】(1)根据直接计算可得;
(2)根据所给数据计算出相关系数,即可说明.
【详解】(1)依题意这个县年垃圾产生总量的平均值为(吨).
(2)依题意,
因为与的相关系数接近,所以与之间具有较强的线性相关关系,可用线性回归模型进行拟合.
16.(1)回归方程为,的现实意义为年收入每增加1千元,估计消费支出增加0.68千元;(2)(户).
【分析】(1)分析题意,按照求回归方程的步骤求出线性回归方程,并进行估计;
(2)根据题意计算样本中达到最富裕的家庭的频率,即可估计全部家庭中达到最富裕的家庭的个数.
【详解】解:(1)由题,可知,,
所以,
故.
所以y关于x的回归方程为.
的现实意义为年收入每增加1千元,估计消费支出增加0.68千元.
(2)由题意可知,8户脱贫家庭的恩格尔系数如下表所示:
家庭(i) 1 2 3 4 5 6 7 8
恩格尔系数 33.3% 33.3% 33.3% 37.1% 32.4% 27.5% 28.6% 27.2%
所以样本中达到最富裕的家庭有3个,
估计该村脱贫家庭中达到最富裕的家庭户数为(户).
【点睛】求线性回归方程的步骤:①求出;②套公式求出;③写出回归方程;④利用回归方程进行预报;
17.(1)列联表见解析
(2)有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异
【分析】(1)直接计算补充列联表即可;
(2)先计算,再和10.828比较作出判断即可.
【详解】(1)补充完整的列联表如下:
一级品 二级品 合计
甲机床 30 70 100
乙机床 60 40 100
合计 90 110 200
(2)∵,
∴有99.9%的把握认为甲机床的产品质量与乙机床的产品质量有差异.
18.(1);
(2)列联表见解析,有的把握认为购买冰墩墩与人的年龄有关.
【分析】(1)运用列举法结合古典概型运算公式进行求解即可;
(2)根据表中数据直接完成列联表,结合题中所给的公式进行计算、表中所给的数据进行判断即可.
【详解】(1)因为年龄在之间抽取的人数为7,有意向购买的人数为,
为7人编号为1,2,3,4,5,6,7,其中有意向购买的人的编号为1,2,3,4,
从7人中抽取2人的所有基本事件为:
,共21种,
其中两人中恰有一人打算购买冰墩墩的基本事件有12种,
故所求概率为:.
(2)由调查表可得:
年龄低于40岁的人数 年龄不低于40岁的人数 总计
有意向购买冰墩墩的人数 50 25 75
无意向购买冰墩墩的人数 5 20 25
总计 55 45 100
,
所以有的把握认为购买冰墩墩与人的年龄有关.
19.(1)可用线性回归模型拟合y与x的关系.
(2)B家庭的损失较大
【分析】(1)计算相关系数,若接近1,则可用线性回归模型拟合与的关系.
(2)A家庭符合二项分布,直接用公式求期望,B家庭先根据题意列出分布列再求期望.
【详解】(1)由题可知
,
故可用线性回归模型拟合y与x的关系.
(2)设A家庭中套中小白兔的人数为,则,
所以.
设A家庭的盈利为元,则,
所以.
设B家庭中套中小白兔的人数为,
则的所有可能取值为0,1,2,3,
,
,
,
,
所以.
设B家庭的盈利为元,则,
所以.
因为,所以B家庭的损失较大
答案第1页,共2页
答案第1页,共2页
