第八章概率 章节练习卷2(含解析)-2023-2024学年高二数学-(苏教版2019选择性必修第二册)
文档属性
| 名称 | 第八章概率 章节练习卷2(含解析)-2023-2024学年高二数学-(苏教版2019选择性必修第二册) |  | |
| 格式 | docx | ||
| 文件大小 | 539.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 22:00:50 | ||
图片预览




文档简介
第八章概率章节练习卷1-2023-2024学年高二数学-(苏教版2019选择性必修第二册)
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.设X是一个离散型随机变量,则下列不能作为X的分布列的一组概率取值的数据是( )
A.,
B.0.1,0.2,0.3,0.4
C.p,
D.,,…,
2.给出下列四个命题:
①15秒内,通过某十字路口的汽车的数量是随机变量;
②在一段时间内,某候车室内候车的旅客人数是随机变量;
③一条河流每年的最大流量是随机变量;
④抛一枚硬币三次,正面向上出现的次数是随机变量.其中真命题的个数是( )
A.1 B.2
C.3 D.4
3.在某电路上有两个独立工作的元件,每次通电后,需要更换元件的概率为0.3,需要更换元件的概率为0.2,则在某次通电后有且只有一个需要更换的条件下,需要更换的概率是( )
A. B. C. D.
4.小明和李华在玩游戏,他们分别从1~9这9个正整数中选出一个数告诉老师,老师经过计算后得知他们选择的两个数不相同,且两数之差为偶数,那么小明选择的数是偶数的概率是( )
A. B. C. D.
5.若随机变量,且,则(X=4)的值是( )
A. B. C. D.
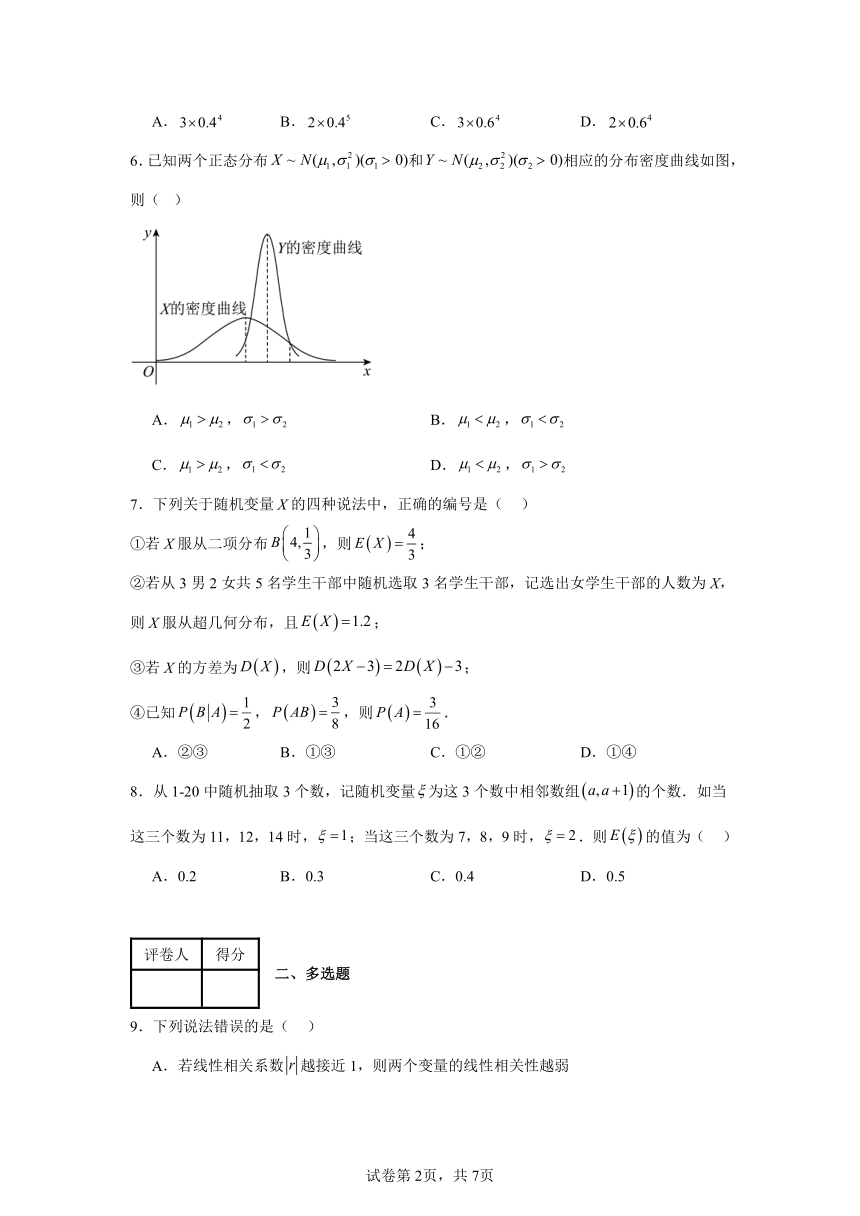
6.已知两个正态分布和相应的分布密度曲线如图,则( )
A., B.,
C., D.,
7.下列关于随机变量X的四种说法中,正确的编号是( )
①若X服从二项分布,则;
②若从3男2女共5名学生干部中随机选取3名学生干部,记选出女学生干部的人数为X,则X服从超几何分布,且;
③若X的方差为,则;
④已知,,则.
A.②③ B.①③ C.①② D.①④
8.从1-20中随机抽取3个数,记随机变量为这3个数中相邻数组的个数.如当这三个数为11,12,14时,;当这三个数为7,8,9时,.则的值为( )
A.0.2 B.0.3 C.0.4 D.0.5
评卷人得分
二、多选题
9.下列说法错误的是( )
A.若线性相关系数越接近1,则两个变量的线性相关性越弱
B.已知随机变量服从正态分布,则其期望
C.已知随机变量服从正态分布,且,则
D.已知一组数据的方差是3,则数据的标准差是12
10.随机变量X的分布列如下:
X 0 1 2
a
则下列说法正确的是( )
A. B. C. D.
11.下列四个命题中为真命题的是( )
A.已知随机变量服从正态分布,若,则
B.已知服从正态分布,且,则
C.二项式的展开式中的常数项是45
D.已知,且,则
评卷人得分
三、填空题
12.已知分布列
Y 1 2 3 4 5 6
P 0.1 x 0.35 0.1 0.15 0.2
则(1)x= ;
(2)P(Y>3)= ;
(3)P(1<Y≤4)= .
13.已知离散型随机变量X的分布列如表所示,则m的值为 .
0 1 2 3
14.一个质地均匀的小正方体,其中三面标有0,两面标有1,另一面标有2,将这个小正方体连续抛掷两次,若用随机变量表示两次中出现向上的面所标的数字之积,则的期望 .
评卷人得分
四、解答题
15.某人每次射击命中目标的概率为0.8,现连续射击3次,求击中目标的次数X的均值和方差.
16.设50件商品中有15件一等品,其余为二等品.现从中随机选购2件,用随机变量X表示所购2件商品中一等品的件数,写出X的概率分布.
17.已知某小学生参加了暑期进行的游泳培训,分别学习自由泳和蛙泳,经过一周训练后,她每次自由泳训练及格的概率为,蛙泳及格的概率为.考核采用积分制,每次自由泳、蛙泳及格分别得1分、2分,不及格均得0分,每次游泳的结果相互独立.若该小学生每天进行3次考核训练,其中自由泳2次,蛙泳1次.
(1)求“该小学生蛙泳不及格且恰好有1次自由泳及格”的概率;
(2)若该小学生的总得分为X,求X的分布列和数学期望.
18.2020年5月1日开始,新版《北京市生活垃圾管理条例》正式实施,垃圾分类标准为厨余垃圾、可回收物、有害垃圾和其他垃圾四类.生活垃圾中有一部分可以回收利用,回收1吨废纸可再造出0.8吨好纸,降低造纸的污染排放,节省造纸能源消耗.某环保小组调查了北京市某垃圾处理厂2020年6月至12月生活垃圾回收情况,其中可回收物中废纸和塑料品的回收量(单位:吨)的折线图如图所示:
(1)现从2020年6月至12月中随机选取1个月,求该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨的概率;
(2)从2020年6月至12月中任意选取2个月,记为选取的这2个月中废纸的回收量超过3.7吨的月份的个数.求的分布列及数学期望.
19.甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为,乙每次投篮命中的概率为,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数的分布列与期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据分布列的性质可知,所有的概率和等于1,且,逐一判断选项即可.
【详解】根据分布列的性质可知,所有的概率之和等于1,且,.
对于A,因为,满足,所以A选项能成为X的分布列的一组概率取值的数据;
对于B,因为,且满足,所以B选项能成为X的分布列的一组概率取值的数据;
对于C,因为,且满足,所以C选项能成为X的分布列的一组概率取值的数据;
对于D,因为,所以D选项不能成为X的分布列的一组概率取值的数据.
故选:D.
2.D
【分析】利用随机变量的定义直接判断即可.
【详解】如果随机试验的结果,可以用一个变量来表示,那么这个变量叫随机变量。
显然,四个命题中的随机试验的结果都可以用一个变量来表示,即都是随机变量,
故四个命题都是真命题,即真命题的个数为.
故选:D.
3.A
【分析】根据题意,结合独立事件的概率乘法公式和条件概率的计算公式,即可求解.
【详解】记事件为在某次通电后 有且只有一个需要更换,事件为需要更换,
则,
由条件概率公式可得.
故选:A.
4.A
【分析】根据条件概率公式求解即可.
【详解】解:设两数之差为偶数为事件,小明选择的数是偶数为事件,
由于他们选择的两个数不相同,且两数之差为偶数,则小明选择的数是偶数的概率为:.
故选:A.
5.A
【分析】先由二项分布的期望公式求出的值,再由二项分布求概率.
【详解】随机变量,则,解得
则
故选:A
6.D
【分析】由正态曲线和均值、标准差的意义判断即可.
【详解】由图象可得的密度曲线的对称轴在的密度曲线的对称轴的左侧,
故,
由图象可得的密度函数的最大值小于的密度函数的最大值,
所以,
故选:D .
7.C
【分析】根据二项分布的期望公式判断①;求出超几何分布的期望判断②;根据方差的性质判断③;根据条件概率公式判断④.
【详解】若X服从二项分布,则,①正确;
选出女学生干部的人数为X的值为,且服从超几何分布,
所以,②正确;
若X的方差为,则,③错误;
因为,,所以,④错误.
故选:C.
8.B
【分析】随机变量的取值为0,1,2,结合变量对应的事件写出概率,算出期望.
【详解】随机变量的取值为0,1,2,
当时,所取的三个数中仅两个数相邻,其中取1,2和19,20,对应取法为17种,其余17情况取法为16种,
,
当时,即所取的三个数中两两相邻,取法有18种,,
所以当时,即所取的三个数彼此不相邻,取法有种,
,
.
故选:B.
9.ABD
【分析】根据线性相关系数的概念可判断A,根据正态分布的概念及性质可判断BC,根据方差的性质可判断D.
【详解】对于A,线性相关系数越接近1,则两个变量的线性相关性越强,故A错误;
对于B,因为X服从正态分布,所以,故B错误
对于C,因为服从正态分布,则其正态分布曲线的对称轴为,
所以,
所以,故C正确;
对于D,根据方差的性质可知的方差为,
故所求标准差为,故D错误.
故选:ABD.
10.BC
【分析】对于A,根据所有概率和为1,可求出,对于B,由求解,对于C,利用期望公式求解,对于D,利用方差公式求解.
【详解】对于A,由题意得,得,所以A错误,
对于B,,所以B正确,
对于C,,所以C正确,
对于D,,所以D错误,
故选:BC
11.BCD
【分析】根据正态分布性质判断A,B选项,根据二项式展开式判断C选项,应用二项分布性质判断D选项.
【详解】 已知随机变量服从正态分布,若,
可得曲线的对称轴为,则,A不正确;
若服从正态分布,且,则,B正确;
二项式的展开式的通项公式为,由,
解得,可得常数项是,C正确;
因为,所以,即,D正确.
故选:BCD.
12. 0.1; 0.45; 0.55.
【分析】(1)由离散型随机变量的各个取值的概率之和为1即可求得x的值;
(2)将Y的值大于3的各种情况的概率值相加即得;
(3)将满足,即的各个概率相加即得.
【详解】解:(1)由概率和为1,∴,解得.
(2).
(3).
故答案为:0.1;0.45;0.55.
【点睛】本题考查离散型随机变量的性质,根据离散型随机变量的各个概率之和为1和离散型随机变量的概率分布有两条基本性质:
(1).;(2).另外离散型随机变量的各个值时互斥的,概率是可加的.
13./
【分析】利用分布列的性质,解关于m的方程,再验证作答.
【详解】依题意,,整理得,解得或,
当时,,,不符合题意,
当时,,,,,符合题意,
所以m的值为.
故答案为:.
14.
【分析】根据题意先求出随机变量的可能取值,然后分别求出随机变量每一个值对应的概率,最后代入离散型随机变量的均值公式即可求解.
【详解】由题意可知:随机变量的可能取值为,
当变量为时,表示两次中至少有一个为,这两个事件是相互独立事件,
所以,
同理;
;
,所以,
故答案为:.
15.
【分析】根据二项分布求得.
【详解】依题意,,
所以.
16.分布列见解析
【分析】根据超几何分布的知识求得的概率分布.
【详解】一等品件,二等品件.
的可能取值为,
,
,
所以的分布列为
17.(1);
(2)分布列见解析,.
【分析】(1)根据独立事件的概率计算公式,结合已知条件,直接计算即可;
(2)求得的取值,以及对应的概率,再结合分布列求数学期望即可.
【详解】(1)记“该小学生蛙泳不及格且恰好有1次自由泳及格”为事件A,
则
(2)X的所有可能取值为0,1,2,3,4,
则,
,
,
,
,
所以X的分布列为:
X 0 1 2 3 4
P
所以X的数学期望.
18.(1)
(2)分布列见解析,
【分析】(1)根据古典概型概率计算公式求得正确答案.
(2)利用超几何分布的分布列的求法求得分布列并求得数学期望.
【详解】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件,
由图知,只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨,∴
(2)6月至12月废纸的回收量超过3.7吨的月份有7月、8月、10月,共3个月.
∴的所有可能取值为0,1,2.
,,,
∴的分布列为:
0 1 2
∴数学期望.
19.(1);(2)分布列见解析,数学期望为
【分析】(1) 本题考查互斥事件的概率,设甲第次投中获胜的事件为,则彼此互斥,分别计算出的概率(可用相互独立事件同时发生的概率公式计算),然后相加即得;
(2) 甲的投篮次数的取舍分别1,2,3,注意这里事件含甲第次投中和第次投不中而接着乙投中,结合(1)的过程可很快求和各事件概率,从而得分布列,并依据期望公式可计算出期望值.
【详解】(1)设甲第i次投中获胜的事件为,则彼此互斥.
甲获胜的事件为.
;;
所以.
所以甲获胜的概率为.
(2)所有可能取的值为1,2,3.
则;
;
.
即X的概率分布列为
1 2 3
所以的数学期望.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.设X是一个离散型随机变量,则下列不能作为X的分布列的一组概率取值的数据是( )
A.,
B.0.1,0.2,0.3,0.4
C.p,
D.,,…,
2.给出下列四个命题:
①15秒内,通过某十字路口的汽车的数量是随机变量;
②在一段时间内,某候车室内候车的旅客人数是随机变量;
③一条河流每年的最大流量是随机变量;
④抛一枚硬币三次,正面向上出现的次数是随机变量.其中真命题的个数是( )
A.1 B.2
C.3 D.4
3.在某电路上有两个独立工作的元件,每次通电后,需要更换元件的概率为0.3,需要更换元件的概率为0.2,则在某次通电后有且只有一个需要更换的条件下,需要更换的概率是( )
A. B. C. D.
4.小明和李华在玩游戏,他们分别从1~9这9个正整数中选出一个数告诉老师,老师经过计算后得知他们选择的两个数不相同,且两数之差为偶数,那么小明选择的数是偶数的概率是( )
A. B. C. D.
5.若随机变量,且,则(X=4)的值是( )
A. B. C. D.
6.已知两个正态分布和相应的分布密度曲线如图,则( )
A., B.,
C., D.,
7.下列关于随机变量X的四种说法中,正确的编号是( )
①若X服从二项分布,则;
②若从3男2女共5名学生干部中随机选取3名学生干部,记选出女学生干部的人数为X,则X服从超几何分布,且;
③若X的方差为,则;
④已知,,则.
A.②③ B.①③ C.①② D.①④
8.从1-20中随机抽取3个数,记随机变量为这3个数中相邻数组的个数.如当这三个数为11,12,14时,;当这三个数为7,8,9时,.则的值为( )
A.0.2 B.0.3 C.0.4 D.0.5
评卷人得分
二、多选题
9.下列说法错误的是( )
A.若线性相关系数越接近1,则两个变量的线性相关性越弱
B.已知随机变量服从正态分布,则其期望
C.已知随机变量服从正态分布,且,则
D.已知一组数据的方差是3,则数据的标准差是12
10.随机变量X的分布列如下:
X 0 1 2
a
则下列说法正确的是( )
A. B. C. D.
11.下列四个命题中为真命题的是( )
A.已知随机变量服从正态分布,若,则
B.已知服从正态分布,且,则
C.二项式的展开式中的常数项是45
D.已知,且,则
评卷人得分
三、填空题
12.已知分布列
Y 1 2 3 4 5 6
P 0.1 x 0.35 0.1 0.15 0.2
则(1)x= ;
(2)P(Y>3)= ;
(3)P(1<Y≤4)= .
13.已知离散型随机变量X的分布列如表所示,则m的值为 .
0 1 2 3
14.一个质地均匀的小正方体,其中三面标有0,两面标有1,另一面标有2,将这个小正方体连续抛掷两次,若用随机变量表示两次中出现向上的面所标的数字之积,则的期望 .
评卷人得分
四、解答题
15.某人每次射击命中目标的概率为0.8,现连续射击3次,求击中目标的次数X的均值和方差.
16.设50件商品中有15件一等品,其余为二等品.现从中随机选购2件,用随机变量X表示所购2件商品中一等品的件数,写出X的概率分布.
17.已知某小学生参加了暑期进行的游泳培训,分别学习自由泳和蛙泳,经过一周训练后,她每次自由泳训练及格的概率为,蛙泳及格的概率为.考核采用积分制,每次自由泳、蛙泳及格分别得1分、2分,不及格均得0分,每次游泳的结果相互独立.若该小学生每天进行3次考核训练,其中自由泳2次,蛙泳1次.
(1)求“该小学生蛙泳不及格且恰好有1次自由泳及格”的概率;
(2)若该小学生的总得分为X,求X的分布列和数学期望.
18.2020年5月1日开始,新版《北京市生活垃圾管理条例》正式实施,垃圾分类标准为厨余垃圾、可回收物、有害垃圾和其他垃圾四类.生活垃圾中有一部分可以回收利用,回收1吨废纸可再造出0.8吨好纸,降低造纸的污染排放,节省造纸能源消耗.某环保小组调查了北京市某垃圾处理厂2020年6月至12月生活垃圾回收情况,其中可回收物中废纸和塑料品的回收量(单位:吨)的折线图如图所示:
(1)现从2020年6月至12月中随机选取1个月,求该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨的概率;
(2)从2020年6月至12月中任意选取2个月,记为选取的这2个月中废纸的回收量超过3.7吨的月份的个数.求的分布列及数学期望.
19.甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为,乙每次投篮命中的概率为,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数的分布列与期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据分布列的性质可知,所有的概率和等于1,且,逐一判断选项即可.
【详解】根据分布列的性质可知,所有的概率之和等于1,且,.
对于A,因为,满足,所以A选项能成为X的分布列的一组概率取值的数据;
对于B,因为,且满足,所以B选项能成为X的分布列的一组概率取值的数据;
对于C,因为,且满足,所以C选项能成为X的分布列的一组概率取值的数据;
对于D,因为,所以D选项不能成为X的分布列的一组概率取值的数据.
故选:D.
2.D
【分析】利用随机变量的定义直接判断即可.
【详解】如果随机试验的结果,可以用一个变量来表示,那么这个变量叫随机变量。
显然,四个命题中的随机试验的结果都可以用一个变量来表示,即都是随机变量,
故四个命题都是真命题,即真命题的个数为.
故选:D.
3.A
【分析】根据题意,结合独立事件的概率乘法公式和条件概率的计算公式,即可求解.
【详解】记事件为在某次通电后 有且只有一个需要更换,事件为需要更换,
则,
由条件概率公式可得.
故选:A.
4.A
【分析】根据条件概率公式求解即可.
【详解】解:设两数之差为偶数为事件,小明选择的数是偶数为事件,
由于他们选择的两个数不相同,且两数之差为偶数,则小明选择的数是偶数的概率为:.
故选:A.
5.A
【分析】先由二项分布的期望公式求出的值,再由二项分布求概率.
【详解】随机变量,则,解得
则
故选:A
6.D
【分析】由正态曲线和均值、标准差的意义判断即可.
【详解】由图象可得的密度曲线的对称轴在的密度曲线的对称轴的左侧,
故,
由图象可得的密度函数的最大值小于的密度函数的最大值,
所以,
故选:D .
7.C
【分析】根据二项分布的期望公式判断①;求出超几何分布的期望判断②;根据方差的性质判断③;根据条件概率公式判断④.
【详解】若X服从二项分布,则,①正确;
选出女学生干部的人数为X的值为,且服从超几何分布,
所以,②正确;
若X的方差为,则,③错误;
因为,,所以,④错误.
故选:C.
8.B
【分析】随机变量的取值为0,1,2,结合变量对应的事件写出概率,算出期望.
【详解】随机变量的取值为0,1,2,
当时,所取的三个数中仅两个数相邻,其中取1,2和19,20,对应取法为17种,其余17情况取法为16种,
,
当时,即所取的三个数中两两相邻,取法有18种,,
所以当时,即所取的三个数彼此不相邻,取法有种,
,
.
故选:B.
9.ABD
【分析】根据线性相关系数的概念可判断A,根据正态分布的概念及性质可判断BC,根据方差的性质可判断D.
【详解】对于A,线性相关系数越接近1,则两个变量的线性相关性越强,故A错误;
对于B,因为X服从正态分布,所以,故B错误
对于C,因为服从正态分布,则其正态分布曲线的对称轴为,
所以,
所以,故C正确;
对于D,根据方差的性质可知的方差为,
故所求标准差为,故D错误.
故选:ABD.
10.BC
【分析】对于A,根据所有概率和为1,可求出,对于B,由求解,对于C,利用期望公式求解,对于D,利用方差公式求解.
【详解】对于A,由题意得,得,所以A错误,
对于B,,所以B正确,
对于C,,所以C正确,
对于D,,所以D错误,
故选:BC
11.BCD
【分析】根据正态分布性质判断A,B选项,根据二项式展开式判断C选项,应用二项分布性质判断D选项.
【详解】 已知随机变量服从正态分布,若,
可得曲线的对称轴为,则,A不正确;
若服从正态分布,且,则,B正确;
二项式的展开式的通项公式为,由,
解得,可得常数项是,C正确;
因为,所以,即,D正确.
故选:BCD.
12. 0.1; 0.45; 0.55.
【分析】(1)由离散型随机变量的各个取值的概率之和为1即可求得x的值;
(2)将Y的值大于3的各种情况的概率值相加即得;
(3)将满足,即的各个概率相加即得.
【详解】解:(1)由概率和为1,∴,解得.
(2).
(3).
故答案为:0.1;0.45;0.55.
【点睛】本题考查离散型随机变量的性质,根据离散型随机变量的各个概率之和为1和离散型随机变量的概率分布有两条基本性质:
(1).;(2).另外离散型随机变量的各个值时互斥的,概率是可加的.
13./
【分析】利用分布列的性质,解关于m的方程,再验证作答.
【详解】依题意,,整理得,解得或,
当时,,,不符合题意,
当时,,,,,符合题意,
所以m的值为.
故答案为:.
14.
【分析】根据题意先求出随机变量的可能取值,然后分别求出随机变量每一个值对应的概率,最后代入离散型随机变量的均值公式即可求解.
【详解】由题意可知:随机变量的可能取值为,
当变量为时,表示两次中至少有一个为,这两个事件是相互独立事件,
所以,
同理;
;
,所以,
故答案为:.
15.
【分析】根据二项分布求得.
【详解】依题意,,
所以.
16.分布列见解析
【分析】根据超几何分布的知识求得的概率分布.
【详解】一等品件,二等品件.
的可能取值为,
,
,
所以的分布列为
17.(1);
(2)分布列见解析,.
【分析】(1)根据独立事件的概率计算公式,结合已知条件,直接计算即可;
(2)求得的取值,以及对应的概率,再结合分布列求数学期望即可.
【详解】(1)记“该小学生蛙泳不及格且恰好有1次自由泳及格”为事件A,
则
(2)X的所有可能取值为0,1,2,3,4,
则,
,
,
,
,
所以X的分布列为:
X 0 1 2 3 4
P
所以X的数学期望.
18.(1)
(2)分布列见解析,
【分析】(1)根据古典概型概率计算公式求得正确答案.
(2)利用超几何分布的分布列的求法求得分布列并求得数学期望.
【详解】(1)记“该垃圾处理厂可回收物中废纸和塑料品的回收量均超过4.0吨”为事件,
由图知,只有8月份的可回收物中废纸和塑料品的回收量均超过4.0吨,∴
(2)6月至12月废纸的回收量超过3.7吨的月份有7月、8月、10月,共3个月.
∴的所有可能取值为0,1,2.
,,,
∴的分布列为:
0 1 2
∴数学期望.
19.(1);(2)分布列见解析,数学期望为
【分析】(1) 本题考查互斥事件的概率,设甲第次投中获胜的事件为,则彼此互斥,分别计算出的概率(可用相互独立事件同时发生的概率公式计算),然后相加即得;
(2) 甲的投篮次数的取舍分别1,2,3,注意这里事件含甲第次投中和第次投不中而接着乙投中,结合(1)的过程可很快求和各事件概率,从而得分布列,并依据期望公式可计算出期望值.
【详解】(1)设甲第i次投中获胜的事件为,则彼此互斥.
甲获胜的事件为.
;;
所以.
所以甲获胜的概率为.
(2)所有可能取的值为1,2,3.
则;
;
.
即X的概率分布列为
1 2 3
所以的数学期望.
答案第1页,共2页
答案第1页,共2页
