列方程解决实际问题 (课件)-五年级下册数学苏教版(共75张PPT)
文档属性
| 名称 | 列方程解决实际问题 (课件)-五年级下册数学苏教版(共75张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 20:35:45 | ||
图片预览











文档简介
(共75张PPT)
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第1课时
1.联系具体情境认识等式,理解和掌握方程的意义,认识方程和等式之间的关系;能根据具体情境里数量间的联系列出相应的方程。
2.经历将现实问题里的数量关系抽象成等式与方程的过程,体会方程是反映数量之间相等关系的数学模型,发展观察、比较和抽象、概括等能力,感受分类的思想和模型思想。
学习目标
【重点】
认识方程的意义,用方程表示简单的数量关系。
【难点】
理解方程的意义。
探究新知
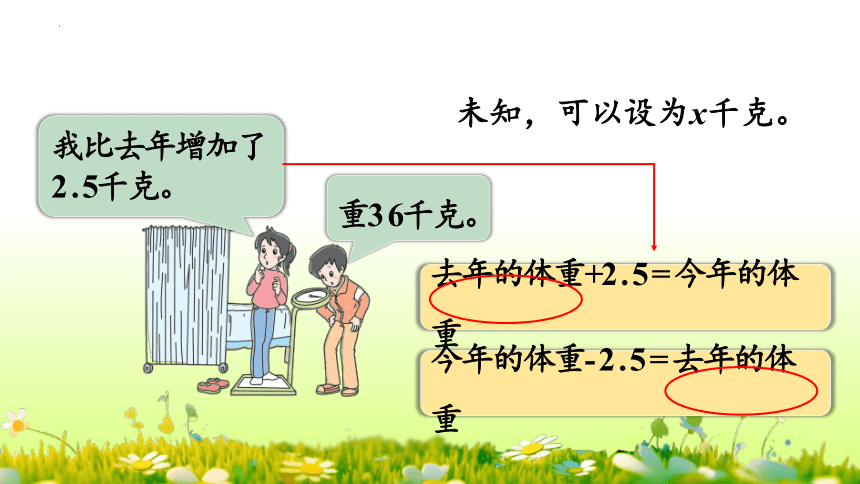
我比去年增加了2 . 5千克。
重3 6千克。
小红去年的体重是多少千克?
我比去年增加了2 . 5千克。
重3 6千克。
去年的体重+2 . 5 = 今年的体重
今年的体重- 2 . 5 = 去年的体重
未知,可以设为x千克。
根据“去年的体重+2.5 =今年的体重”列方程。
解:设小红去年的体重是 x千克。
x + 2.5 = 36
x = 36-2.5
x = 33.5
这句话必须写出来,解释未知数表示的含义。
方程中的x作为一个未知数,是一个数值,因此求出的解后面不加单位名称。
根据“今年的体重-2.5 =去年的体重”列方程。
解:设小红去年的体重是 x千克。
36-x = 2.5
36-x +x = 2.5 +x
36 = 2.5 +x
2.5 +x = 36
x = 33.5
答:小红去年的体重是32.5千克。
先检查方程列得是否正确,再检验方程的解。
你打算怎样检验?与同学交流。
看两种方程的解答结果是否相同。
列方程解决实际问题需要注意什么?
先弄清题意,找出未知量,并用字母表示。
要根据题中数量之间的相等关系列方程。
求出答案后,还要检验结果是否正确。
练一练
一头蓝鲸重165吨,大约是一头非洲象的33倍。这头非洲象大约重多少吨?(先把数量间的相等关系填写完整,再列方程解答)
一头非洲象的体重×33 = 一头蓝鲸的体重
165吨
未知量,设为x吨
33 x = 165
检验:
把x = 5代入原方程,
左边=33×5=165,
左边=右边,
所以x = 5是原方程的解。
答:这头非洲象大约重5吨。
解:设这头非洲象大约重x吨。
33 x = 165
33 x ÷33 = 165÷33
x = 5
检验:
把x = 5代入原方程,
左边=33×5=165,
左边=右边,
所以x = 5是原方程的解。
答:这头非洲象大约重5吨。
解:设这头非洲象大约重x吨。
33 x = 165
33 x ÷33 = 165÷33
x = 5
课堂练习
1.解方程。
x+56 = 102
解:x = 102-56
x = 46
x-970 = 270
解:x = 270+970
x = 1240
15x = 3
解:x = 3÷15
x = 0.2
x÷0.8 = 1.25
解:x = 1.25×0.8
x = 1
x-16=36
解:设白键有x个。
x=36+16
x=52
答:白键有52个。
钢琴的黑键有36个,比白键少16个。
2.
0.52x =23.4
解:设用电x千瓦·时。
x =23.4÷0.52
x =45
答:用电45千瓦·时。
3.某市居民用电每千瓦·时的价格是0.52元。芳芳家上个月付电费23.4元,用电多少千瓦·时?
1.5x =144
解:宽应是x厘米。
x =144÷1.5
x =96
答:宽应是96厘米。
4.中华人民共和国国旗的长应是宽的1.5倍。一面国旗长144厘米,宽应是多少厘米?
课堂小结
这节课你有什么收获?
1.抓住题目中的关键语句找出等量关系来列方程;
2.解方程并检验作答。
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第2课时
1. 理解和掌握列方程解决简单实际问题的方法与过程,能根据题中数量之间的相等关系列出方程,解方程求出问题结果。
2. 经历分析数量之间相等关系、列方程解决问题的过程,了解列方程解决简单实际问题的思考方法,体会模型思想,提高解决问题的能力。
学习目标
【重点】
列方程解决简单实际问题。
【难点】
理解列方程解决实际问题的思路。
探究新知
西安大雁塔高64.7米,比小雁塔高度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
小雁塔的高度×2-21.9=大雁塔的高度
2x-21.9=64.7
64.7米
未知量,设为x
小雁塔的高度×2-大雁塔的高度=21.9
2x-64.7=21.9
64.7米
未知量,设为x
西安大雁塔高64.7米,比小雁塔度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
小雁塔的高度×2=大雁塔的高度+21.9
2x=64.7+21.9
64.7米
未知量,设为x
西安大雁塔高64.7米,比小雁塔高度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
根据“小雁塔的高度×2-21.9=大雁塔的高度”解决问题。
解:设小雁塔高x米。
2x-21.9=64.7
2x-21.9+21.9 = 64.7+21.9
2x = 86.6
x = 43.3
检验:
把x = 43.3代入原方程,
左边=2×43.3-21.9=64.7
左边=右边,
所以x = 43.3是原方程的解。
答:小雁塔高43.3米。
根据“小雁塔的高度×2-大雁塔的高度=21.9”解决问题。
解:设小雁塔高x米。
2x-64.7= 21.9
2x-64.7+64.7 = 21.9+64.7
2x = 86.6
x = 43.3
根据“小雁塔的高度×2=大雁塔的高度+21.9”解决问题。
解:设小雁塔高x米。
2x = 21.9+64.7
2x = 86.6
x = 43.3
练一练
杭州湾跨海大桥全长大约36千米,比香港青马大桥的16倍还多0.8千米。香港青马大桥全长大约多少千米?(先把数量间的相等关系填写完整,再列方程解答)
( )大桥的长度×16 + 0 . 8 =( )大桥的长度
香港青马
杭州湾跨海
16x+0.8=36
解:设香港青马大桥全长大约 x 千米。
16x+0.8-0.8=36-0.8
16x=35.2
x=2.2
答:香港青马大桥全长大约2.2千米。
香港青马大桥的长度×16 + 0 . 8 =杭州湾跨海大桥的长度
课堂练习
1.解方程。
4x+20 = 56
解:4x = 56-20
4x = 36
1.8+7x = 3.9
解:7x = 3.9-1.8
7x = 2.1
x = 6
x = 0.3
(1)张大伯家的果园有桃树x棵,梨树比桃树的3倍多15棵。有梨树( )棵。
3x+15
(2)王叔叔在鱼池里放养鲫鱼x尾。放养的鳊鱼比鲫鱼的4倍少80尾,放养鳊鱼( )尾。
4x-80
2.在括号里填写含有字母的式子。
桃树的数量×3+15=梨树的数量
放养的鳊鱼的数量×4-80=放养的鲫鱼的数量
2x+20=110
解:设猫的最快时速是x千米/小时。
2x=110-20
2x=90
答:猫的最快时速是45千米/小时。
x=45
3.猎豹是世界上跑得最快的动物,时速能达到110千米/小时,比猫的最快时速的2倍还多20。猫的最快时速是多少千米/小时?
猫的最快时速×2+20=猎豹的最快时速
4x-13=365
解:设水星绕太阳一周大约要用x天。
4x=365+13
4x=378
答:水星绕太阳一周大约要用95天。
x=94.5
4.地球绕太阳一周大约要365天,比水星绕太阳一周所用时间的4倍少13天。水星绕太阳一周大约要用多少天?
水星绕太阳一周所用时间×4 + 13 =地球绕太阳一周所用时间
1. 甲比乙的几倍多(或少)几,已知甲,求乙的问题,可设乙为x, 根据乙×倍数±几=甲,列出形如ax±b=c的方程进行求解。
课堂小结
这节课你有什么收获?
这节课你有什么收获?
形如ax+ b =c(a≠0)的方程的解法:
解: ax + b – b =c-b
ax=c-b
ax + b = c
x=(c-b)÷a
这节课你有什么收获?
形如ax - b =c(a≠0)的方程的解法:
解: ax – b+b =c+b
ax=c+b
ax – b = c
x=(c+b)÷a
2.列方程解决实际问题的一般步骤:
(1)根据题中信息找出等量关系;
(2)设未知数;
(3)列出方程并检验;
(4)写出答语。
这节课你有什么收获?
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第3课时
1.进一步理解和掌握列方程解决实际问题的方法,能理解稍复杂实际问题(和倍、差倍问题)的数量关系,能正确列方程解稍复杂的实际问题,并学会解形如ax±bx=c的简易方程。
2.理解稍复杂实际问题的等量关系,进一步掌握列方程
解决实际问题的思路,发展符号意识和几何直观思想,
体会模型思想。
学习目标
【重点】
列方程解决稍复杂的实际问题和解方程。
【难点】
理解用含有同一字母的式子表示两个
未知数量。
陆地面积 × 3 = 水面面积
探究新知
北京颐和园占地290公顷,其中水面面积大约是陆地面积的3倍。颐和园的陆地和水面面积大约各有多少公顷?
9
1份
3份
题中有两个未知的数量,应该设哪个未知量为x?另一个未知量怎么表示?
把作为比较标准的量(陆地面积)设为x,同时用含有x的式子表示另一个未知量(水面面积)。
北京颐和园占地290公顷,其中水面面积大约是陆地面积的3倍。颐和园的陆地和水面面积大约各有多少公顷?
你能根据题意把线段图和等量关系式填写完整吗?
x公顷
( )公顷
陆地面积
水面面积
( )公顷
( )面积 +( )面积=颐和园的占地面积
3x
290
陆地
水面
x
3x
290
+
=
解:设颐和园的陆地面积大约有x公顷,则水面面积大约有3x公顷。
x + 3x = 290
4x = 290
x = 72.5
3 x = 217.5
你会用“把得数代入原题”的方法检验吗?
看陆地面积加水面面积是不是等于290公顷。
72.5+217.5=290(公顷)
看水面面积是不是陆地面积的3倍。
217.5÷72.5=3
答:颐和园的陆地面积大约有72.5公顷,水面面积大约有217.5公顷。
练一练
1.在括号里填写含有字母的式子。
(1)黄花有x朵,红花的朵数是黄花的3倍。黄花和红花一共有( )朵,红花比黄花多( )朵。
(2)商店运来电冰箱x台,运来洗衣机的台数是电冰箱的2.3倍。运来的电冰箱和洗衣机一共有( )台,电冰箱比洗衣机少( )台。
4x
2x
3.3x
1.3x
2.4x – x = 2.1
1份,设为x
2.地球表面海洋面积大约是陆地面积的2.4倍,比陆地面积多2.1亿平方千米。
海洋面积和陆地面积大约各是多少亿平方千米?
陆地面积×2.4=海洋面积
海洋面积-陆地面积=2.1
2.4x
2.4x - x =2.1
解:设陆地面积大约是x亿平方千米,则海洋面积大约是2.4x亿平方千米。
1.4x=2.1
x=1.5
2.4 x=2.4×1.5=3.6
答:陆地面积大约是1.5亿平方千米,则海洋面积大约是3.6亿平方千米。
课堂练习
1.解方程。
2x+ 3x = 60
解:5x = 60
x = 12
3.6x - 2.8x = 12
解:0.8x = 12
x = 15
100x - x = 198
解:99x = 198
x = 2
我今年的年龄正好是你的4倍。
我比你小30岁。
2.小红和爸爸今年各多少岁?
4x – x = 30
1份,设为x
小红的年龄×4=爸爸的年龄
爸爸的年龄-小红的年龄=30
4x
我今年的年龄正好是你的4倍。
我比你小30岁。
解:设小红今年x岁,则爸爸今年4 x岁。
4 x - x = 30
3 x = 30
x = 10
答:小红今年10岁,爸爸今年40岁。
4 x = 4×10 = 40
2.小红和爸爸今年各多少岁?
四年级去的人数×1.2=五年级去的人数
3.同学们参观“抗震救灾英雄事迹展览”。四、五年级一共去了264人,五年级去的人数是四年级的1.2倍。两个年级各去了多少人?
x + 1.2x = 30
1份,设为x
四年级去的人数+小红的年龄五年级去的人数=264
1.2x
3.同学们参观“抗震救灾英雄事迹展览”。四、五年级一共去了264人,五年级去的人数是四年级的1.2倍。两个年级各去了多少人?
解:设四年级去了x人,则五年级去了1.2 x人。
x + 1.2x = 264
2.2 x = 264
x = 120
答:四年级去了120人,则五年级去了144人。
1.2 x = 1.2×120 = 144
课堂小结
1.列方程解决含有两个未知量的问题时,
先设其中一个未知量为x(通常设一倍量为x),
再用含有x的式子表示另一个未知量,
然后根据等量关系,列出形如ax±bx=c的方程,
最后进行解答。
这节课你有什么收获?
2.形如ax±bx = c的方程的解法:
这节课你有什么收获?
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第4课时
1.进一步理解和掌握列方程解决实际问题的方法,能理解三步计算实际问题(相遇问题)的等量关系,能正确列方程解三步计算的实际问题,能解形如ax±bc=d的方程。
2.理解三步计算实际问题的数量关系,了解、掌握找等量关系的方法,进一步体会模型思想,发展分析能力。
学习目标
【重点】
列方程解决三步计算实际问题和解方程。
【难点】
理解方程表示的数量关系。
探究新知
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
10
你能根据题意把线段图填写完整吗?
( )千米/时
( )千米/时
客车
货车
( )千米
95
540
客车行的路程+货车行的路程=总路程
找出图中的等量关系,与同学交流。
速度和×时间=总路程
你能根据“客车行的路程+货车行的路程=总路程”,列出方程并解答吗?
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
解:设货车的速度是x千米/时。
95×3 + 3x = 540
285 + 3x = 540
3x = 540-285
3x = 255
x = 85
检验结果是否正确,并说说还可以怎样列方程。
检验:
把x = 85代入原方程,
左边=95×3+3×85=540,
左边=右边,
所以x = 85是原方程的解。
答:货车的速度是85千米/时。
( 95 + x )×3 = 540
95 + x = 540÷3
95 + x = 180
x = 85
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
根据“速度和×时间=总路程”列方程。
解:设货车的速度是x千米/时。
答:货车的速度是85千米/时。
列方程解决实际问题的关键是什么?
应用学过的公式、数量关系式或者画图,可以帮助我们寻找等量关系。
列方程解决实际问题的关键是找出题中的等量关系。
练一练
两艘轮船从一个码头往相反方向开出,8小时后两船相距400千米。甲船的速度是26千米/时,乙船的速度是多少千米/时?(先利用线段图整理条件和问题,再列方程解答)
400
26
甲( )千米/时
乙( )千米/时
相距( )千米
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
根据“甲船行的路程+乙船行的路程=总路程”列方程。
解:设乙船的速度是x千米/时。
26×8 + 8x = 400
208 + 8x = 400
8x = 400-208
8x = 192
x = 24
答:乙船的速度是24千米/时。
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
( 26 + x )×8 = 400
26 + x = 400÷8
26 + x = 50
x = 24
根据“速度和×时间=总路程”列方程。
解:设乙船的速度是x千米/时。
答:乙船的速度是85千米/时。
课堂练习
1.解方程。
5x+ 6x = 12.1
解:11x = 12.1
x = 1.1
18×2 + 3x = 60
解:36+3x = 60
3x = 24
x =8
5x -10 = 150
解:5x = 160
x = 32
1.5x - x = 1
解:0.5x = 1
x = 2
0.2×2 + 0.2x = 5
解:0.4+0.2x = 5
0.2x = 4.6
4x -8×5 = 20
解:4x -40 = 160
4x = 200
x =23
x = 50
2.周永家和李刚家相距600米,他们同时从自己家出发,相向而行,经过4分钟相遇。周永每分钟走72米,李刚每分钟走多少米?
解:
设李刚每分钟走x米。
(x + 72)×4 = 600
x + 72 = 600÷4
x + 72 = 150
x = 78
答:李刚每分钟走78 米。
2.周永家和李刚家相距600米,他们同时从自己家出发,相向而行,经过4分钟相遇。周永每分钟走72米,李刚每分钟走多少米?
解:
设李刚每分钟走x米。
4 x + 72×4 = 600
4x + 288 = 600
4x = 312
x = 78
答:李刚每分钟走78 米。
3.甲、乙两人骑摩托车同时从相距190千米的两个城市出发,相向而行。甲的速度是36千米/时,乙的速度是40千米/时,经过多少小时两人相遇?
解:
设经过x小时两人相遇。
36 x + 40 x = 190
76 x = 190
x = 2.5
答:经过2.5小时两人相遇。
(36 + 40 )x = 190
76 x = 190
x = 2.5
4.妈妈买了一些苹果和梨,一共用去20元。根据右表中的数据列方程求出梨的单价。
解:
设梨的单价是 x 元/千克。
3×4 + 2 x = 20
12+2x = 20
2x = 8
x = 4
答:梨的单价是4元/千克。
4
课堂小结
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
这节课你有什么收获?
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
这节课你有什么收获?
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
这节课你有什么收获?
Thank you!
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第1课时
1.联系具体情境认识等式,理解和掌握方程的意义,认识方程和等式之间的关系;能根据具体情境里数量间的联系列出相应的方程。
2.经历将现实问题里的数量关系抽象成等式与方程的过程,体会方程是反映数量之间相等关系的数学模型,发展观察、比较和抽象、概括等能力,感受分类的思想和模型思想。
学习目标
【重点】
认识方程的意义,用方程表示简单的数量关系。
【难点】
理解方程的意义。
探究新知
我比去年增加了2 . 5千克。
重3 6千克。
小红去年的体重是多少千克?
我比去年增加了2 . 5千克。
重3 6千克。
去年的体重+2 . 5 = 今年的体重
今年的体重- 2 . 5 = 去年的体重
未知,可以设为x千克。
根据“去年的体重+2.5 =今年的体重”列方程。
解:设小红去年的体重是 x千克。
x + 2.5 = 36
x = 36-2.5
x = 33.5
这句话必须写出来,解释未知数表示的含义。
方程中的x作为一个未知数,是一个数值,因此求出的解后面不加单位名称。
根据“今年的体重-2.5 =去年的体重”列方程。
解:设小红去年的体重是 x千克。
36-x = 2.5
36-x +x = 2.5 +x
36 = 2.5 +x
2.5 +x = 36
x = 33.5
答:小红去年的体重是32.5千克。
先检查方程列得是否正确,再检验方程的解。
你打算怎样检验?与同学交流。
看两种方程的解答结果是否相同。
列方程解决实际问题需要注意什么?
先弄清题意,找出未知量,并用字母表示。
要根据题中数量之间的相等关系列方程。
求出答案后,还要检验结果是否正确。
练一练
一头蓝鲸重165吨,大约是一头非洲象的33倍。这头非洲象大约重多少吨?(先把数量间的相等关系填写完整,再列方程解答)
一头非洲象的体重×33 = 一头蓝鲸的体重
165吨
未知量,设为x吨
33 x = 165
检验:
把x = 5代入原方程,
左边=33×5=165,
左边=右边,
所以x = 5是原方程的解。
答:这头非洲象大约重5吨。
解:设这头非洲象大约重x吨。
33 x = 165
33 x ÷33 = 165÷33
x = 5
检验:
把x = 5代入原方程,
左边=33×5=165,
左边=右边,
所以x = 5是原方程的解。
答:这头非洲象大约重5吨。
解:设这头非洲象大约重x吨。
33 x = 165
33 x ÷33 = 165÷33
x = 5
课堂练习
1.解方程。
x+56 = 102
解:x = 102-56
x = 46
x-970 = 270
解:x = 270+970
x = 1240
15x = 3
解:x = 3÷15
x = 0.2
x÷0.8 = 1.25
解:x = 1.25×0.8
x = 1
x-16=36
解:设白键有x个。
x=36+16
x=52
答:白键有52个。
钢琴的黑键有36个,比白键少16个。
2.
0.52x =23.4
解:设用电x千瓦·时。
x =23.4÷0.52
x =45
答:用电45千瓦·时。
3.某市居民用电每千瓦·时的价格是0.52元。芳芳家上个月付电费23.4元,用电多少千瓦·时?
1.5x =144
解:宽应是x厘米。
x =144÷1.5
x =96
答:宽应是96厘米。
4.中华人民共和国国旗的长应是宽的1.5倍。一面国旗长144厘米,宽应是多少厘米?
课堂小结
这节课你有什么收获?
1.抓住题目中的关键语句找出等量关系来列方程;
2.解方程并检验作答。
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第2课时
1. 理解和掌握列方程解决简单实际问题的方法与过程,能根据题中数量之间的相等关系列出方程,解方程求出问题结果。
2. 经历分析数量之间相等关系、列方程解决问题的过程,了解列方程解决简单实际问题的思考方法,体会模型思想,提高解决问题的能力。
学习目标
【重点】
列方程解决简单实际问题。
【难点】
理解列方程解决实际问题的思路。
探究新知
西安大雁塔高64.7米,比小雁塔高度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
小雁塔的高度×2-21.9=大雁塔的高度
2x-21.9=64.7
64.7米
未知量,设为x
小雁塔的高度×2-大雁塔的高度=21.9
2x-64.7=21.9
64.7米
未知量,设为x
西安大雁塔高64.7米,比小雁塔度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
小雁塔的高度×2=大雁塔的高度+21.9
2x=64.7+21.9
64.7米
未知量,设为x
西安大雁塔高64.7米,比小雁塔高度的2倍少21.9米。小雁塔高多少米?
8
大雁塔与小雁塔的高度之间有什么相等关系?
根据“小雁塔的高度×2-21.9=大雁塔的高度”解决问题。
解:设小雁塔高x米。
2x-21.9=64.7
2x-21.9+21.9 = 64.7+21.9
2x = 86.6
x = 43.3
检验:
把x = 43.3代入原方程,
左边=2×43.3-21.9=64.7
左边=右边,
所以x = 43.3是原方程的解。
答:小雁塔高43.3米。
根据“小雁塔的高度×2-大雁塔的高度=21.9”解决问题。
解:设小雁塔高x米。
2x-64.7= 21.9
2x-64.7+64.7 = 21.9+64.7
2x = 86.6
x = 43.3
根据“小雁塔的高度×2=大雁塔的高度+21.9”解决问题。
解:设小雁塔高x米。
2x = 21.9+64.7
2x = 86.6
x = 43.3
练一练
杭州湾跨海大桥全长大约36千米,比香港青马大桥的16倍还多0.8千米。香港青马大桥全长大约多少千米?(先把数量间的相等关系填写完整,再列方程解答)
( )大桥的长度×16 + 0 . 8 =( )大桥的长度
香港青马
杭州湾跨海
16x+0.8=36
解:设香港青马大桥全长大约 x 千米。
16x+0.8-0.8=36-0.8
16x=35.2
x=2.2
答:香港青马大桥全长大约2.2千米。
香港青马大桥的长度×16 + 0 . 8 =杭州湾跨海大桥的长度
课堂练习
1.解方程。
4x+20 = 56
解:4x = 56-20
4x = 36
1.8+7x = 3.9
解:7x = 3.9-1.8
7x = 2.1
x = 6
x = 0.3
(1)张大伯家的果园有桃树x棵,梨树比桃树的3倍多15棵。有梨树( )棵。
3x+15
(2)王叔叔在鱼池里放养鲫鱼x尾。放养的鳊鱼比鲫鱼的4倍少80尾,放养鳊鱼( )尾。
4x-80
2.在括号里填写含有字母的式子。
桃树的数量×3+15=梨树的数量
放养的鳊鱼的数量×4-80=放养的鲫鱼的数量
2x+20=110
解:设猫的最快时速是x千米/小时。
2x=110-20
2x=90
答:猫的最快时速是45千米/小时。
x=45
3.猎豹是世界上跑得最快的动物,时速能达到110千米/小时,比猫的最快时速的2倍还多20。猫的最快时速是多少千米/小时?
猫的最快时速×2+20=猎豹的最快时速
4x-13=365
解:设水星绕太阳一周大约要用x天。
4x=365+13
4x=378
答:水星绕太阳一周大约要用95天。
x=94.5
4.地球绕太阳一周大约要365天,比水星绕太阳一周所用时间的4倍少13天。水星绕太阳一周大约要用多少天?
水星绕太阳一周所用时间×4 + 13 =地球绕太阳一周所用时间
1. 甲比乙的几倍多(或少)几,已知甲,求乙的问题,可设乙为x, 根据乙×倍数±几=甲,列出形如ax±b=c的方程进行求解。
课堂小结
这节课你有什么收获?
这节课你有什么收获?
形如ax+ b =c(a≠0)的方程的解法:
解: ax + b – b =c-b
ax=c-b
ax + b = c
x=(c-b)÷a
这节课你有什么收获?
形如ax - b =c(a≠0)的方程的解法:
解: ax – b+b =c+b
ax=c+b
ax – b = c
x=(c+b)÷a
2.列方程解决实际问题的一般步骤:
(1)根据题中信息找出等量关系;
(2)设未知数;
(3)列出方程并检验;
(4)写出答语。
这节课你有什么收获?
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第3课时
1.进一步理解和掌握列方程解决实际问题的方法,能理解稍复杂实际问题(和倍、差倍问题)的数量关系,能正确列方程解稍复杂的实际问题,并学会解形如ax±bx=c的简易方程。
2.理解稍复杂实际问题的等量关系,进一步掌握列方程
解决实际问题的思路,发展符号意识和几何直观思想,
体会模型思想。
学习目标
【重点】
列方程解决稍复杂的实际问题和解方程。
【难点】
理解用含有同一字母的式子表示两个
未知数量。
陆地面积 × 3 = 水面面积
探究新知
北京颐和园占地290公顷,其中水面面积大约是陆地面积的3倍。颐和园的陆地和水面面积大约各有多少公顷?
9
1份
3份
题中有两个未知的数量,应该设哪个未知量为x?另一个未知量怎么表示?
把作为比较标准的量(陆地面积)设为x,同时用含有x的式子表示另一个未知量(水面面积)。
北京颐和园占地290公顷,其中水面面积大约是陆地面积的3倍。颐和园的陆地和水面面积大约各有多少公顷?
你能根据题意把线段图和等量关系式填写完整吗?
x公顷
( )公顷
陆地面积
水面面积
( )公顷
( )面积 +( )面积=颐和园的占地面积
3x
290
陆地
水面
x
3x
290
+
=
解:设颐和园的陆地面积大约有x公顷,则水面面积大约有3x公顷。
x + 3x = 290
4x = 290
x = 72.5
3 x = 217.5
你会用“把得数代入原题”的方法检验吗?
看陆地面积加水面面积是不是等于290公顷。
72.5+217.5=290(公顷)
看水面面积是不是陆地面积的3倍。
217.5÷72.5=3
答:颐和园的陆地面积大约有72.5公顷,水面面积大约有217.5公顷。
练一练
1.在括号里填写含有字母的式子。
(1)黄花有x朵,红花的朵数是黄花的3倍。黄花和红花一共有( )朵,红花比黄花多( )朵。
(2)商店运来电冰箱x台,运来洗衣机的台数是电冰箱的2.3倍。运来的电冰箱和洗衣机一共有( )台,电冰箱比洗衣机少( )台。
4x
2x
3.3x
1.3x
2.4x – x = 2.1
1份,设为x
2.地球表面海洋面积大约是陆地面积的2.4倍,比陆地面积多2.1亿平方千米。
海洋面积和陆地面积大约各是多少亿平方千米?
陆地面积×2.4=海洋面积
海洋面积-陆地面积=2.1
2.4x
2.4x - x =2.1
解:设陆地面积大约是x亿平方千米,则海洋面积大约是2.4x亿平方千米。
1.4x=2.1
x=1.5
2.4 x=2.4×1.5=3.6
答:陆地面积大约是1.5亿平方千米,则海洋面积大约是3.6亿平方千米。
课堂练习
1.解方程。
2x+ 3x = 60
解:5x = 60
x = 12
3.6x - 2.8x = 12
解:0.8x = 12
x = 15
100x - x = 198
解:99x = 198
x = 2
我今年的年龄正好是你的4倍。
我比你小30岁。
2.小红和爸爸今年各多少岁?
4x – x = 30
1份,设为x
小红的年龄×4=爸爸的年龄
爸爸的年龄-小红的年龄=30
4x
我今年的年龄正好是你的4倍。
我比你小30岁。
解:设小红今年x岁,则爸爸今年4 x岁。
4 x - x = 30
3 x = 30
x = 10
答:小红今年10岁,爸爸今年40岁。
4 x = 4×10 = 40
2.小红和爸爸今年各多少岁?
四年级去的人数×1.2=五年级去的人数
3.同学们参观“抗震救灾英雄事迹展览”。四、五年级一共去了264人,五年级去的人数是四年级的1.2倍。两个年级各去了多少人?
x + 1.2x = 30
1份,设为x
四年级去的人数+小红的年龄五年级去的人数=264
1.2x
3.同学们参观“抗震救灾英雄事迹展览”。四、五年级一共去了264人,五年级去的人数是四年级的1.2倍。两个年级各去了多少人?
解:设四年级去了x人,则五年级去了1.2 x人。
x + 1.2x = 264
2.2 x = 264
x = 120
答:四年级去了120人,则五年级去了144人。
1.2 x = 1.2×120 = 144
课堂小结
1.列方程解决含有两个未知量的问题时,
先设其中一个未知量为x(通常设一倍量为x),
再用含有x的式子表示另一个未知量,
然后根据等量关系,列出形如ax±bx=c的方程,
最后进行解答。
这节课你有什么收获?
2.形如ax±bx = c的方程的解法:
这节课你有什么收获?
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
ax+bx = c
解:(a+b)x = c
(a+b)x÷(a+b) = c÷(a+b)
x = c÷(a+b)
一 简易方程
列方程解决实际问题
数学苏教版五年级下册
第4课时
1.进一步理解和掌握列方程解决实际问题的方法,能理解三步计算实际问题(相遇问题)的等量关系,能正确列方程解三步计算的实际问题,能解形如ax±bc=d的方程。
2.理解三步计算实际问题的数量关系,了解、掌握找等量关系的方法,进一步体会模型思想,发展分析能力。
学习目标
【重点】
列方程解决三步计算实际问题和解方程。
【难点】
理解方程表示的数量关系。
探究新知
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
10
你能根据题意把线段图填写完整吗?
( )千米/时
( )千米/时
客车
货车
( )千米
95
540
客车行的路程+货车行的路程=总路程
找出图中的等量关系,与同学交流。
速度和×时间=总路程
你能根据“客车行的路程+货车行的路程=总路程”,列出方程并解答吗?
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
解:设货车的速度是x千米/时。
95×3 + 3x = 540
285 + 3x = 540
3x = 540-285
3x = 255
x = 85
检验结果是否正确,并说说还可以怎样列方程。
检验:
把x = 85代入原方程,
左边=95×3+3×85=540,
左边=右边,
所以x = 85是原方程的解。
答:货车的速度是85千米/时。
( 95 + x )×3 = 540
95 + x = 540÷3
95 + x = 180
x = 85
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
根据“速度和×时间=总路程”列方程。
解:设货车的速度是x千米/时。
答:货车的速度是85千米/时。
列方程解决实际问题的关键是什么?
应用学过的公式、数量关系式或者画图,可以帮助我们寻找等量关系。
列方程解决实际问题的关键是找出题中的等量关系。
练一练
两艘轮船从一个码头往相反方向开出,8小时后两船相距400千米。甲船的速度是26千米/时,乙船的速度是多少千米/时?(先利用线段图整理条件和问题,再列方程解答)
400
26
甲( )千米/时
乙( )千米/时
相距( )千米
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
根据“甲船行的路程+乙船行的路程=总路程”列方程。
解:设乙船的速度是x千米/时。
26×8 + 8x = 400
208 + 8x = 400
8x = 400-208
8x = 192
x = 24
答:乙船的速度是24千米/时。
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
( 26 + x )×8 = 400
26 + x = 400÷8
26 + x = 50
x = 24
根据“速度和×时间=总路程”列方程。
解:设乙船的速度是x千米/时。
答:乙船的速度是85千米/时。
课堂练习
1.解方程。
5x+ 6x = 12.1
解:11x = 12.1
x = 1.1
18×2 + 3x = 60
解:36+3x = 60
3x = 24
x =8
5x -10 = 150
解:5x = 160
x = 32
1.5x - x = 1
解:0.5x = 1
x = 2
0.2×2 + 0.2x = 5
解:0.4+0.2x = 5
0.2x = 4.6
4x -8×5 = 20
解:4x -40 = 160
4x = 200
x =23
x = 50
2.周永家和李刚家相距600米,他们同时从自己家出发,相向而行,经过4分钟相遇。周永每分钟走72米,李刚每分钟走多少米?
解:
设李刚每分钟走x米。
(x + 72)×4 = 600
x + 72 = 600÷4
x + 72 = 150
x = 78
答:李刚每分钟走78 米。
2.周永家和李刚家相距600米,他们同时从自己家出发,相向而行,经过4分钟相遇。周永每分钟走72米,李刚每分钟走多少米?
解:
设李刚每分钟走x米。
4 x + 72×4 = 600
4x + 288 = 600
4x = 312
x = 78
答:李刚每分钟走78 米。
3.甲、乙两人骑摩托车同时从相距190千米的两个城市出发,相向而行。甲的速度是36千米/时,乙的速度是40千米/时,经过多少小时两人相遇?
解:
设经过x小时两人相遇。
36 x + 40 x = 190
76 x = 190
x = 2.5
答:经过2.5小时两人相遇。
(36 + 40 )x = 190
76 x = 190
x = 2.5
4.妈妈买了一些苹果和梨,一共用去20元。根据右表中的数据列方程求出梨的单价。
解:
设梨的单价是 x 元/千克。
3×4 + 2 x = 20
12+2x = 20
2x = 8
x = 4
答:梨的单价是4元/千克。
4
课堂小结
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
这节课你有什么收获?
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
这节课你有什么收获?
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
这节课你有什么收获?
Thank you!
