第九章 统计 章节练习卷2(含解析)-2023-2024学年高二数学-(苏教版2019选择性必修第二册)
文档属性
| 名称 | 第九章 统计 章节练习卷2(含解析)-2023-2024学年高二数学-(苏教版2019选择性必修第二册) |  | |
| 格式 | docx | ||
| 文件大小 | 649.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 22:03:24 | ||
图片预览




文档简介
第九章统计章节练习卷2-2023-2024学年高二数学-(苏教版2019选择性必修第二册)
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.某校随机调查了100名高中生是否喜欢篮球,按照男女区分得到列联表,经计算得.根据独立性检验的相关知识,对照下表,可以认为有( )把握喜欢篮球与性别有关.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
A. B. C. D.
2.利用独立性检验考察两个变量X与Y是否有关系,通过2×2列联表进行独立性检验.经计算,那么认为X与Y是有关系,这个结论错误的可能性不超过( )
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
A.0.001 B.0.005 C.0.05 D.0.01
3.对于线性回归直线,样本点的残差为( )
A. B. C. D.
4.1.两个分类变量X和Y,其2×2列联表如表,对同一样本,以下数据能说明X与Y有关联的可能性最大的一组为( ).
X Y 合计
3 6 9
m 8
合计 14
A. B. C. D.
5.为研究变量的相关关系,收集得到如下数据:
5 6 7 8 9
9 8 6 4 3
若由最小二乘法求得关于的经验回归方程为,则据此计算残差为0的样本点是( )
A. B. C. D.
6.根据分类变量与的成对样本数据,计算得到,依据的独立性检验,结论为( )
A.变量与不独立
B.变量与不独立,这个结论犯错误的概率超过0.01
C.变量与独立
D.变量与独立,这个结论犯错误的概率不超过0.01
7.新型冠状病毒(2019-NCoV)因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名,为考察某种药物预防该疾病的效果,进行动物试验,得到如下列联表:
患病 未患病 总计
服用药 10 45 55
未服药 20 30 50
总计 30 75 105
下列说法正确的是( )
参考数据:,
0.05 0.01
3.841 6.635
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
8.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
合计
附:
P(K2≥k0) 0.05 0.025 0.010 0.005
k0 3.841 5.024 6.635 7.879
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按97.5%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按97.5%的可靠性要求,不能认为“成绩与班级有关系”
评卷人得分
二、多选题
9.已知某产品的单价以及销量情况统计如下表所示,由表中数据求得经验回归方程,则下列说法正确的是( )
单价(元) 4 5 6 7 8 9
销是(件) 90 84 83 80 75 68
A.销量的平均数为80件
B.根据经验回归方程可以测得,单价每上升1元,销量就减少4件
C.
D.根据经验回归方程可以预测,单价为10元时,销量为66件
10.下列四个命题中为真命题的是( )
A.若随机变量服从二项分布,则
B.若随机变量服从正态分布,且,则
C.已知一组数据的方差是3,则的方差也是3
D.对具有线性相关关系的变量,其线性回归方程为,若样本点的中心为,则实数的值是4
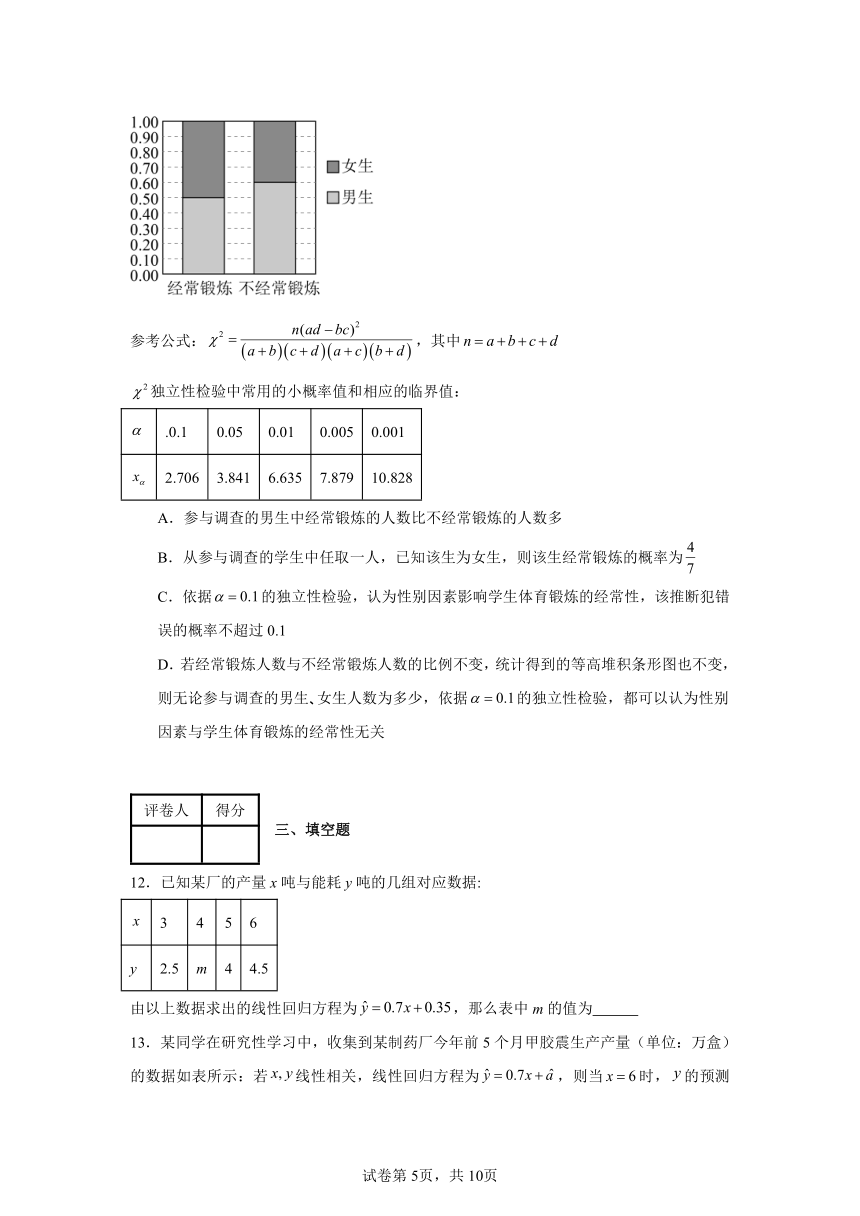
11.为了有针对性地提高学生体育锻炼的积极性,哈尔滨市某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,随机抽取了300名学生,对他们是否经常锻炼的情况进行了调查,调查发现经常锻炼人数是不经常锻炼人数的2倍,绘制其等高堆积条形图,如图所示,则下列说法不正确的是( )
参考公式:,其中
独立性检验中常用的小概率值和相应的临界值:
.0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.参与调查的男生中经常锻炼的人数比不经常锻炼的人数多
B.从参与调查的学生中任取一人,已知该生为女生,则该生经常锻炼的概率为
C.依据的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.1
D.若经常锻炼人数与不经常锻炼人数的比例不变,统计得到的等高堆积条形图也不变,则无论参与调查的男生 女生人数为多少,依据的独立性检验,都可以认为性别因素与学生体育锻炼的经常性无关
评卷人得分
三、填空题
12.已知某厂的产量x吨与能耗y吨的几组对应数据:
3 4 5 6
y 2.5 m 4 4.5
由以上数据求出的线性回归方程为,那么表中m的值为
13.某同学在研究性学习中,收集到某制药厂今年前5个月甲胶震生产产量(单位:万盒)的数据如表所示:若线性相关,线性回归方程为,则当时,的预测值为 万盒.
(月份) 1 2 3 4 5
(万盒) 5 6 5 6 8
14.某校团委对“学生性别和喜欢网络游戏是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢网络游戏的人数占男生人数的,女生喜欢网络游戏的人数占女生人数的.若根据独立性检验认为喜欢网络游戏和性别有关,且此推断犯错误的概率超过0.01但不超过0.05,则被调查的学生中男生可能有 人.(请将所有可能的结果都填在横线上)
附表:,其中.
0.050 0.010
3.841 6.635
评卷人得分
四、解答题
15.2021年是中国加入世界贸易组织20周年,“入世”是中国对外开放的一个里程碑,中国已经连续11年成为货物贸易出口第一大国,经济全球化是历史潮流,大势所趋.“入世”20年,中国的发展证明,世界经济离不开中国,中国发展也离不开世界.下表是中国2016~2020这5年来的国内生产总值(GDP)数据,已知年份代码和国内生产总值呈线性相关关系.
年份 2016 2017 2018 2019 2020
年份代码x 1 2 3 4 5
国内生产总值y/万亿美元 11.2 12.3 13.9 14.3 14.7
(1)求年份代码x和国内生产总值y的回归直线方程
(2)预测2022年的国内生产总值.
参考数据:.参考公式:线性回归方程中,.
16.如果x与y线性相关,那么y与x也线性相关吗?为什么?
17.某棉纺厂为了解一批棉花的质量,在该批棉花中随机抽取了容量为120的样本,测量每个样本棉花的纤维长度(单位:mm,纤维长度是棉花质量的重要指标),所得数据均在区间内,将其按组距为2分组,制作成如图所示的频率分布直方图,其中纤维长度不小于28mm的棉花为优质棉.
(1)求频率分布直方图中的值;
(2)已知抽取的容量为120的样本棉花产自于两个试验区,部分数据如下2×2列联表:
试验区 试验区 合计
优质棉 10
非优质棉 30
合计 120
将2×2列联表补充完整,并判断是否有99.9%的把握认为优质棉与两个试验区有关系.
注:①独立性检验的临界值表:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
②,其中.
18.从某校学生中随机抽取了200名男生和100名女生,其中对滑冰运动没有兴趣的有90人,女生中有60人对滑冰运动有兴趣.为探究学生对滑冰运动的兴趣与性别的关系,列出列联表如下:
有兴趣 没有兴趣 合计
男
女 60
合计 300
(1)请将上述列联表补充完整;
(2)能否有的把握认为对滑冰运动有无兴趣与性别有关?
附:,其中.
0.100 0.050 0.010 0.005 0.001
2.06 3.841 6.635 7.879 10.828
19.下面给出了根据我国年—2022年水果人均占有量(单位:kg)和年份代码绘制的散点图和线性回归方程的残差图(2016年—2022年的年份代码分别为1~7).
(1)根据散点图分析与之间的相关关系;
(2)根据散点图相应数据计算得,,求关于的线性回归方程(数据精确到);
(3)根据线性回归方程的残差图,分析线性回归方程的拟合效果.
附:回归方程中的斜率和截距的最小二乘法估计公式分别为
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据的值以及表格可得答案.
【详解】,
有把握认为喜欢篮球与性别有关,
故选:B.
2.C
【分析】利用独立性检验思想及检验值,在表中读取对应数据即可.
【详解】根据检验结果,可知,
所以这个结论错误的可能性不超过0.050,即可知C正确.
故选:C
3.A
【分析】
根据残差的定义可求得结果.
【详解】对于线性回归方程,当时,,故残差为.
故选:A.
4.D
【分析】根据给定条件,依次计算的预测值并比较大小作答.
【详解】由给定的2×2列联表,
对于A,,的预测值,
对于B,,的预测值
对于C,,的预测值,
对于D,,的预测值,
显然,因此选项D中数据求得的预测值最大,说明说明X与Y有关联的可能性最大.
故选:D
5.C
【分析】先求出回归方程的样本中心点,从而可求得,再根据残差的定义可判断.
【详解】由题意可得:,
即样本中心点为,可得,解得,
所以,可得
5 6 7 8 9
9 8 6 4 3
9.2 7.6 6 4.4 2.8
0
所以残差为0的样本点是.
故选:C.
6.A
【分析】直接利用独立性检验的知识求解.
【详解】按照独立性检验的知识及比对参数值,当,我们可以得到变量与不独立,故排除选项C,D;
依据的独立性检验,,
所以变量与不独立,这个结论犯错误的概率不超过,故A正确,B错误.
故选:A
7.A
【分析】根据列联表计算,对照临界值即可得出结论.
【详解】根据列联表,计算,
由临界值表可知,
有95%的把握认为药物有效,A正确
故选:A
8.C
【分析】根据题中条件计算可判断选项A、B;根据列联表计算出的值,即可判断选项C,D.
【详解】由题意知,成绩优秀的学生数是,
成绩非优秀的学生数是75,所以,
选项A、B错误;
根据列联表中的数据,
得到
因此有97.5%的把握认为“成绩与班级有关系”.
故C正确,D错误,
故选:C.
9.ABD
【分析】根据数据先算出样本中心和 ,再根据回归方程逐项计算.
【详解】 ,故正确;
将 代入回归方程得 故回归方程为 ,
由于回归方程的斜率为-4,故正确,C错误;
根据回归方程可以预测,单价为10元时,销量为件,故正确;
故选:.
10.AC
【分析】由二项分布的期望公式判断A;由正态分布的性质判断B;由方差的性质判断C;由回归方程必过样本中心点求解可判断D.
【详解】对于A,由于,则,故A正确;
对于B,,故,故B错误;
对于C,的方差是3,则的方差不变,故C正确;
对于D,回归方程必过样本中心点,则,解得,故D错误.
故选:AC.
11.BCD
【分析】根据数表计算人数判断A选项,根据古典概型公式判断B选项,根据的值及独立性检验判断C,D选项.
【详解】对于A,由题意知经常锻炼人数是不经常锻炼人数的2倍,
故经常锻炼人数为200人,不经常锻炼人数为100人,
故男生中经常锻炼的人数为人,不经常锻炼的人数为人,
故男生中经常锻炼的人数比不经常锻炼的人数多,A正确;
对于B,经常锻炼的女生人数为人,不经常锻炼的人数为人,
故从参与调查的学生中任取一人,已知该生为女生,则该生经常锻炼的概率为,B错误;
对于C,由题意结合男女生中经常锻炼和不经常锻炼的人数,可得列联表:
经常锻炼 不经常锻炼 合计
男 100 60 160
女 100 40 140
合计 200 100 300
则,
故依据的独立性检验,认为性别因素与学生体育锻炼的经常性无关,该推断犯错误的概率不超过0.1,C错误;
对于D,假设抽取名学生,由题意可得:
经常锻炼 不经常锻炼 合计
男 200 120 320
女 200 80 280
合计 400 200 600
则此时,
故依据的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.05,D错误,
故选:BCD
12.3
【分析】中心点在线性回归方程上,求解中心点,带入求参数.
【详解】因为, 又因,所以.
故答案为:3.
13./
【分析】
根据样本中心点求得,进而求得预测值.
【详解】,
所以,所以,
当时,万盒.
故答案为:
14.45,50,55,60,65
【分析】利用独立性检验表达列联表及观测值可解得答案.
【详解】设男生有x人,由题意可得列联表如下,
喜欢 不喜欢 合计
男生 x
女生 x
合计
若认为喜欢网络游戏和性别有关,且该推断犯错误的概率超过0.01但不超过0.05,
则.
∵,
∴,解得,
又x为5的整数倍,∴被调查的学生中男生可能人数为45,50,55,60,65.
故答案为:45,50,55,60,65.
15.(1)
(2)16.88万亿美元
【分析】(1)根据最小二乘法即可求解线性回归方程,(2)利用线性回归方程代入即可预测.
【详解】(1),
,
,
所以,
,
所以年份代码x和国内生产总值y的回归直线方程
(2)令,得,
所以2022年的国内生产总值大约为16.88万亿美元.
16.y与x也线性相关,理由见见解析.
【分析】由相关系数公式结合x与y线性相关即可判断.
【详解】不妨设x与y线性相关系数为,其中,所以y与x的线性相关系数为,所以y与x也线性相关.
17.(1)
(2)列联表见解析,没有99.9%的把握认为优质棉与两个试验区有关系.
【分析】(1)根据频率分布直方图可知所有小矩形面积之和为1,可得;(2)由样本容量为120可得优质棉样本数为30,可完成2×2列联表,计算可得即可得出结论.
【详解】(1)由频率分布直方图可知,所有小矩形面积之和为1,即,
解得;
(2)抽取的优质棉样本数为,则非优质棉样本数为90;
根据表格已有数据可得试验区优质棉样本数为20,试验区非优质棉样本数为60;
则2×2列联表如下:
A试验区 B试验区 合计
优质棉 10 20 30
非优质棉 60 30 90
合计 70 50 120
因此,
所以,没有99.9%的把握认为优质棉与两个试验区有关系.
18.(1)列联表见解析
(2)有的把握认为对滑冰运动有无兴趣与性别有关
【分析】(1)直接根据题意完成表格即可;
(2)计算出的值即可得结果.
【详解】(1)补充完整的列联表如下:
有兴趣 没有兴趣 合计
男 150 50 200
女 60 40 100
合计 210 90 300
(2)∵,
∴有的把握认为对滑冰运动有无兴趣与性别有关.
19.(1)与成线性相关,且为正相关
(2)关于的线性回归方程为
(3)拟合效果较好,回归方程的预报精度较高
【分析】(1)根据散点图可以看出,散点均匀的分布在一条直线附近,故与成线性相关;
(2)根据给出信息,分别计算出,的平均值,代入最小二乘法估计公式,即可得到回归方程;
(3)根据所给残差图分别区域的宽度分析即可.
【详解】(1)解:根据散点图可知,散点均匀的分布在一条直线附近,且随着的增大,增大,故与成线性相关,且为正相关;
(2)解:依题意,,,
,
,
,
所以关于的线性回归方程为:;
(3)解:由残差图可以看出,残差对应点分布在水平带状区域内,且宽度较窄,说明拟合效果较好,回归方程的预报精度较高.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.某校随机调查了100名高中生是否喜欢篮球,按照男女区分得到列联表,经计算得.根据独立性检验的相关知识,对照下表,可以认为有( )把握喜欢篮球与性别有关.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
A. B. C. D.
2.利用独立性检验考察两个变量X与Y是否有关系,通过2×2列联表进行独立性检验.经计算,那么认为X与Y是有关系,这个结论错误的可能性不超过( )
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
A.0.001 B.0.005 C.0.05 D.0.01
3.对于线性回归直线,样本点的残差为( )
A. B. C. D.
4.1.两个分类变量X和Y,其2×2列联表如表,对同一样本,以下数据能说明X与Y有关联的可能性最大的一组为( ).
X Y 合计
3 6 9
m 8
合计 14
A. B. C. D.
5.为研究变量的相关关系,收集得到如下数据:
5 6 7 8 9
9 8 6 4 3
若由最小二乘法求得关于的经验回归方程为,则据此计算残差为0的样本点是( )
A. B. C. D.
6.根据分类变量与的成对样本数据,计算得到,依据的独立性检验,结论为( )
A.变量与不独立
B.变量与不独立,这个结论犯错误的概率超过0.01
C.变量与独立
D.变量与独立,这个结论犯错误的概率不超过0.01
7.新型冠状病毒(2019-NCoV)因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名,为考察某种药物预防该疾病的效果,进行动物试验,得到如下列联表:
患病 未患病 总计
服用药 10 45 55
未服药 20 30 50
总计 30 75 105
下列说法正确的是( )
参考数据:,
0.05 0.01
3.841 6.635
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
8.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 非优秀 总计
甲班 10 b
乙班 c 30
合计
附:
P(K2≥k0) 0.05 0.025 0.010 0.005
k0 3.841 5.024 6.635 7.879
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按97.5%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按97.5%的可靠性要求,不能认为“成绩与班级有关系”
评卷人得分
二、多选题
9.已知某产品的单价以及销量情况统计如下表所示,由表中数据求得经验回归方程,则下列说法正确的是( )
单价(元) 4 5 6 7 8 9
销是(件) 90 84 83 80 75 68
A.销量的平均数为80件
B.根据经验回归方程可以测得,单价每上升1元,销量就减少4件
C.
D.根据经验回归方程可以预测,单价为10元时,销量为66件
10.下列四个命题中为真命题的是( )
A.若随机变量服从二项分布,则
B.若随机变量服从正态分布,且,则
C.已知一组数据的方差是3,则的方差也是3
D.对具有线性相关关系的变量,其线性回归方程为,若样本点的中心为,则实数的值是4
11.为了有针对性地提高学生体育锻炼的积极性,哈尔滨市某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,随机抽取了300名学生,对他们是否经常锻炼的情况进行了调查,调查发现经常锻炼人数是不经常锻炼人数的2倍,绘制其等高堆积条形图,如图所示,则下列说法不正确的是( )
参考公式:,其中
独立性检验中常用的小概率值和相应的临界值:
.0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.参与调查的男生中经常锻炼的人数比不经常锻炼的人数多
B.从参与调查的学生中任取一人,已知该生为女生,则该生经常锻炼的概率为
C.依据的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.1
D.若经常锻炼人数与不经常锻炼人数的比例不变,统计得到的等高堆积条形图也不变,则无论参与调查的男生 女生人数为多少,依据的独立性检验,都可以认为性别因素与学生体育锻炼的经常性无关
评卷人得分
三、填空题
12.已知某厂的产量x吨与能耗y吨的几组对应数据:
3 4 5 6
y 2.5 m 4 4.5
由以上数据求出的线性回归方程为,那么表中m的值为
13.某同学在研究性学习中,收集到某制药厂今年前5个月甲胶震生产产量(单位:万盒)的数据如表所示:若线性相关,线性回归方程为,则当时,的预测值为 万盒.
(月份) 1 2 3 4 5
(万盒) 5 6 5 6 8
14.某校团委对“学生性别和喜欢网络游戏是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢网络游戏的人数占男生人数的,女生喜欢网络游戏的人数占女生人数的.若根据独立性检验认为喜欢网络游戏和性别有关,且此推断犯错误的概率超过0.01但不超过0.05,则被调查的学生中男生可能有 人.(请将所有可能的结果都填在横线上)
附表:,其中.
0.050 0.010
3.841 6.635
评卷人得分
四、解答题
15.2021年是中国加入世界贸易组织20周年,“入世”是中国对外开放的一个里程碑,中国已经连续11年成为货物贸易出口第一大国,经济全球化是历史潮流,大势所趋.“入世”20年,中国的发展证明,世界经济离不开中国,中国发展也离不开世界.下表是中国2016~2020这5年来的国内生产总值(GDP)数据,已知年份代码和国内生产总值呈线性相关关系.
年份 2016 2017 2018 2019 2020
年份代码x 1 2 3 4 5
国内生产总值y/万亿美元 11.2 12.3 13.9 14.3 14.7
(1)求年份代码x和国内生产总值y的回归直线方程
(2)预测2022年的国内生产总值.
参考数据:.参考公式:线性回归方程中,.
16.如果x与y线性相关,那么y与x也线性相关吗?为什么?
17.某棉纺厂为了解一批棉花的质量,在该批棉花中随机抽取了容量为120的样本,测量每个样本棉花的纤维长度(单位:mm,纤维长度是棉花质量的重要指标),所得数据均在区间内,将其按组距为2分组,制作成如图所示的频率分布直方图,其中纤维长度不小于28mm的棉花为优质棉.
(1)求频率分布直方图中的值;
(2)已知抽取的容量为120的样本棉花产自于两个试验区,部分数据如下2×2列联表:
试验区 试验区 合计
优质棉 10
非优质棉 30
合计 120
将2×2列联表补充完整,并判断是否有99.9%的把握认为优质棉与两个试验区有关系.
注:①独立性检验的临界值表:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
②,其中.
18.从某校学生中随机抽取了200名男生和100名女生,其中对滑冰运动没有兴趣的有90人,女生中有60人对滑冰运动有兴趣.为探究学生对滑冰运动的兴趣与性别的关系,列出列联表如下:
有兴趣 没有兴趣 合计
男
女 60
合计 300
(1)请将上述列联表补充完整;
(2)能否有的把握认为对滑冰运动有无兴趣与性别有关?
附:,其中.
0.100 0.050 0.010 0.005 0.001
2.06 3.841 6.635 7.879 10.828
19.下面给出了根据我国年—2022年水果人均占有量(单位:kg)和年份代码绘制的散点图和线性回归方程的残差图(2016年—2022年的年份代码分别为1~7).
(1)根据散点图分析与之间的相关关系;
(2)根据散点图相应数据计算得,,求关于的线性回归方程(数据精确到);
(3)根据线性回归方程的残差图,分析线性回归方程的拟合效果.
附:回归方程中的斜率和截距的最小二乘法估计公式分别为
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据的值以及表格可得答案.
【详解】,
有把握认为喜欢篮球与性别有关,
故选:B.
2.C
【分析】利用独立性检验思想及检验值,在表中读取对应数据即可.
【详解】根据检验结果,可知,
所以这个结论错误的可能性不超过0.050,即可知C正确.
故选:C
3.A
【分析】
根据残差的定义可求得结果.
【详解】对于线性回归方程,当时,,故残差为.
故选:A.
4.D
【分析】根据给定条件,依次计算的预测值并比较大小作答.
【详解】由给定的2×2列联表,
对于A,,的预测值,
对于B,,的预测值
对于C,,的预测值,
对于D,,的预测值,
显然,因此选项D中数据求得的预测值最大,说明说明X与Y有关联的可能性最大.
故选:D
5.C
【分析】先求出回归方程的样本中心点,从而可求得,再根据残差的定义可判断.
【详解】由题意可得:,
即样本中心点为,可得,解得,
所以,可得
5 6 7 8 9
9 8 6 4 3
9.2 7.6 6 4.4 2.8
0
所以残差为0的样本点是.
故选:C.
6.A
【分析】直接利用独立性检验的知识求解.
【详解】按照独立性检验的知识及比对参数值,当,我们可以得到变量与不独立,故排除选项C,D;
依据的独立性检验,,
所以变量与不独立,这个结论犯错误的概率不超过,故A正确,B错误.
故选:A
7.A
【分析】根据列联表计算,对照临界值即可得出结论.
【详解】根据列联表,计算,
由临界值表可知,
有95%的把握认为药物有效,A正确
故选:A
8.C
【分析】根据题中条件计算可判断选项A、B;根据列联表计算出的值,即可判断选项C,D.
【详解】由题意知,成绩优秀的学生数是,
成绩非优秀的学生数是75,所以,
选项A、B错误;
根据列联表中的数据,
得到
因此有97.5%的把握认为“成绩与班级有关系”.
故C正确,D错误,
故选:C.
9.ABD
【分析】根据数据先算出样本中心和 ,再根据回归方程逐项计算.
【详解】 ,故正确;
将 代入回归方程得 故回归方程为 ,
由于回归方程的斜率为-4,故正确,C错误;
根据回归方程可以预测,单价为10元时,销量为件,故正确;
故选:.
10.AC
【分析】由二项分布的期望公式判断A;由正态分布的性质判断B;由方差的性质判断C;由回归方程必过样本中心点求解可判断D.
【详解】对于A,由于,则,故A正确;
对于B,,故,故B错误;
对于C,的方差是3,则的方差不变,故C正确;
对于D,回归方程必过样本中心点,则,解得,故D错误.
故选:AC.
11.BCD
【分析】根据数表计算人数判断A选项,根据古典概型公式判断B选项,根据的值及独立性检验判断C,D选项.
【详解】对于A,由题意知经常锻炼人数是不经常锻炼人数的2倍,
故经常锻炼人数为200人,不经常锻炼人数为100人,
故男生中经常锻炼的人数为人,不经常锻炼的人数为人,
故男生中经常锻炼的人数比不经常锻炼的人数多,A正确;
对于B,经常锻炼的女生人数为人,不经常锻炼的人数为人,
故从参与调查的学生中任取一人,已知该生为女生,则该生经常锻炼的概率为,B错误;
对于C,由题意结合男女生中经常锻炼和不经常锻炼的人数,可得列联表:
经常锻炼 不经常锻炼 合计
男 100 60 160
女 100 40 140
合计 200 100 300
则,
故依据的独立性检验,认为性别因素与学生体育锻炼的经常性无关,该推断犯错误的概率不超过0.1,C错误;
对于D,假设抽取名学生,由题意可得:
经常锻炼 不经常锻炼 合计
男 200 120 320
女 200 80 280
合计 400 200 600
则此时,
故依据的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.05,D错误,
故选:BCD
12.3
【分析】中心点在线性回归方程上,求解中心点,带入求参数.
【详解】因为, 又因,所以.
故答案为:3.
13./
【分析】
根据样本中心点求得,进而求得预测值.
【详解】,
所以,所以,
当时,万盒.
故答案为:
14.45,50,55,60,65
【分析】利用独立性检验表达列联表及观测值可解得答案.
【详解】设男生有x人,由题意可得列联表如下,
喜欢 不喜欢 合计
男生 x
女生 x
合计
若认为喜欢网络游戏和性别有关,且该推断犯错误的概率超过0.01但不超过0.05,
则.
∵,
∴,解得,
又x为5的整数倍,∴被调查的学生中男生可能人数为45,50,55,60,65.
故答案为:45,50,55,60,65.
15.(1)
(2)16.88万亿美元
【分析】(1)根据最小二乘法即可求解线性回归方程,(2)利用线性回归方程代入即可预测.
【详解】(1),
,
,
所以,
,
所以年份代码x和国内生产总值y的回归直线方程
(2)令,得,
所以2022年的国内生产总值大约为16.88万亿美元.
16.y与x也线性相关,理由见见解析.
【分析】由相关系数公式结合x与y线性相关即可判断.
【详解】不妨设x与y线性相关系数为,其中,所以y与x的线性相关系数为,所以y与x也线性相关.
17.(1)
(2)列联表见解析,没有99.9%的把握认为优质棉与两个试验区有关系.
【分析】(1)根据频率分布直方图可知所有小矩形面积之和为1,可得;(2)由样本容量为120可得优质棉样本数为30,可完成2×2列联表,计算可得即可得出结论.
【详解】(1)由频率分布直方图可知,所有小矩形面积之和为1,即,
解得;
(2)抽取的优质棉样本数为,则非优质棉样本数为90;
根据表格已有数据可得试验区优质棉样本数为20,试验区非优质棉样本数为60;
则2×2列联表如下:
A试验区 B试验区 合计
优质棉 10 20 30
非优质棉 60 30 90
合计 70 50 120
因此,
所以,没有99.9%的把握认为优质棉与两个试验区有关系.
18.(1)列联表见解析
(2)有的把握认为对滑冰运动有无兴趣与性别有关
【分析】(1)直接根据题意完成表格即可;
(2)计算出的值即可得结果.
【详解】(1)补充完整的列联表如下:
有兴趣 没有兴趣 合计
男 150 50 200
女 60 40 100
合计 210 90 300
(2)∵,
∴有的把握认为对滑冰运动有无兴趣与性别有关.
19.(1)与成线性相关,且为正相关
(2)关于的线性回归方程为
(3)拟合效果较好,回归方程的预报精度较高
【分析】(1)根据散点图可以看出,散点均匀的分布在一条直线附近,故与成线性相关;
(2)根据给出信息,分别计算出,的平均值,代入最小二乘法估计公式,即可得到回归方程;
(3)根据所给残差图分别区域的宽度分析即可.
【详解】(1)解:根据散点图可知,散点均匀的分布在一条直线附近,且随着的增大,增大,故与成线性相关,且为正相关;
(2)解:依题意,,,
,
,
,
所以关于的线性回归方程为:;
(3)解:由残差图可以看出,残差对应点分布在水平带状区域内,且宽度较窄,说明拟合效果较好,回归方程的预报精度较高.
答案第1页,共2页
答案第1页,共2页
