期中复习 课本习题整理(1-4单元课件)-五年级下册数学人教版(共351张PPT)
文档属性
| 名称 | 期中复习 课本习题整理(1-4单元课件)-五年级下册数学人教版(共351张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 53.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 20:40:16 | ||
图片预览









文档简介
(共351张PPT)
知识点归纳总结:
1.点----线----面----体;
2.根据一个方向观察到的形状摆小正方体,有多种摆法,无法确定立体图形形状;
3.根据三个方向观察到的形状摆小正方体,只有一种摆法。
4.从正面、左面、上面三个不同的方向观察同一组物体而画出的图形就是三视图。
一、观察物体(三)
小明摆了一个几何体,从三个方向看到的图形如下:
小明摆的几何体是( )。
A
一、观察物体(三)
右边的三个图形分别是从什么方向看到的?填一填。
从( )面看
从( )面看
从( )面看
上
前
左
辨认从三个不同方向观察到的图形
一、观察物体(三)
从上面看
从正面看
最少需要 小正方体,
最多需要 小正方体;
6个
7个
一、观察物体(三)
倍数与因数的概念:
二、因数与倍数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
注意:
1.因数与倍数是相互依存的,不能单独存在;
2.一个数的因数的个数是有限的,倍数的个数是无限的;
3.一个数的最大因数=最小倍数=它本身;
4.一个数因数的求法:成对的按顺序找;
5.一个数倍数的求法:依次乘以自然数。
奇数与偶数的运算规律:
奇数±奇数=偶数
奇数±偶数=奇数
偶数±偶数=偶数
奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
2、3、5的倍数特征:
◆ 2的倍数特征:个位上是0、2、4、6、8的数都是2的倍数;
◆ 3的倍数特征:一个数各位上的数的和是三的倍数,这个数
叫3的倍数;
◆ 5的倍数特征:个位上是0、5的数都是5的倍数。
奇数、偶数、质数和合数:
◆奇数:
◆偶数:
◆质数:
◆合数:
不能被2整除的数叫奇数(个位上是1,3,5,7,9的数);
能被2整除的数叫偶数(个位上是0,2,4,6,8的数);
只有1和它本身两个因数的数叫做质数;
除了1和它本身还有其他因数的数叫做合数。
◆1只有一个因数,所以1既不是质数,也不是合数。
特殊的数:
最小的偶数是( ),最小的奇数是( ),最小的质数是( ),最小的合数是( ),( )既不是质数,也不是合数。
0
1
2
4
1
在自然数中,有一个数很特殊,大家知道是哪一个数吗?
0÷3=0
0×3=0
0×10=0
0÷10=0
例如:
0有很多特殊性,如0乘一个数还得0,0不能作除数等。
注意:为了方便,在研究因数和倍数的时候,我们所指的
数是自然数(一般不包括0)。
下面说法对吗?
(2)1.8÷0.3=6,0.3是1.8的因数,1.8是0.3的倍数。
(1)6÷5=1.2, 5是6的因数,6是5的倍数。
(4)54÷6=9,6是因数,54是倍数 。
(3)24÷3=8, 8是24的因数,24是8的倍数 。
( )
( )
( )
( )
×
×
√
×
(说说你的理由)
辨一辨。 (对的画“√”,错的画“ ”)
1. 6 ÷ 6 =1,这里 6 既是因数,也是倍数。
( )
2. 28是7的倍数。
( )
24 和 16 都是 8 的倍数, 8 既是 24 的因数,也
是16的因数。
( )
4. 自然数 1,2,3,…都是 1 的倍数。
( )
5. 3.6 是 9 的倍数。
( )
√
√
√
×
仔细观察找到的因数,你们发现了什么?
18的因数有 1 ,2 ,3 ,6 ,9 ,18 。
30的因数有 1 ,2 ,3 ,5 ,6 ,10 ,15 ,30 。
36的因数有 1 ,2 ,3 ,4 ,6 ,9 ,12 ,18 ,36 。
1
1
1
一个数的最小因数是_____,最大因数是________。
一个数的因数的个数是________。
1
它本身
有限的
仔细观察,你发现这些数的倍数有哪些特征呢?
2的倍数有 2 ,4 ,6 ,8 ,10 ,12,···
3的倍数有 3,6,9,12,15,18,···
5的倍数有 5,10,15,20,25,30,···
一个数的最小倍数是_______,_____最大倍数。
一个数的倍数的个数是________。
它本身
无限的
没有
判断下面的说法是否正确,并说一说你的理由。
(1)1是1,2,3,…的因数。 ( )
(2)8的倍数只有16,24,32,40,48 ( )
(3)36÷9=4,所以36是9的倍数。 ( )
(4)5.7是3的倍数。 ( )
√
×
×
√
【选自教材P7 练习二 第5题】
1、在26、12和13这三个数中,( )是( )的倍数,( )是( )的因数。
2、一个数,千位上是最小的质数,百位上是最小的奇数,个位是最小的合数,其余数位上的数字是0,这个数写作( )。
3、一个数的最大因数是36 ,这个数是( ),这个数的最小倍数是( )。
4、一个两位数同时是2、5、3的倍数,这个两位数最大是( ),最小是( )。
26
13
13
26
2104
36
36
90
30
从0、4、5、8、9中选取三个数字组成三位数:
(1)在能被2整除的数中,最大的是( ),最小的是( );
(2)在能被3整除的数中,最大的是( ),最小的是( );
(3)在能被5整除的数中,最大的是( ),最小的是( )。
984
408
984
405
985
405
2.菲菲家的电话号码是一个八位数,记为:ABCDEFGH。已知:A是最小的质数,B是最小的合数,C既不是质数也不是合数,D是比最小的质数小2的数,E是10以内最大的合数,F只有因数1和5,G是8的最大因数,H是6的最小倍数。
答:菲菲家的电话号码是:24109586。
猜数游戏。
【选自教材P8 练习二 第7题】
它是42的因数,
又是7的倍数。
它可能是7,14,
21,42中的一个。
我知道了,它是_______。
42
它也是2和3的
倍数。
一个数比20小,它既是2的倍数,又有因数7,这个数
是( )。
一个数的最大因数和最小倍数都是9,这个数是( )。
14
9
填空。
(1)1 的因数有 个,7 的因数有 个,10 的因数有 个。
(2)一个数的最大因数和最小倍数都是18,这个数是 。
(3)一个数的最小倍数是1,这个数是 。
1
2
4
【选自教材P8 练习二 第6题】
18
1
按要求填写数字。
【选自教材P11 练习三 第2题】
(1) 两个数位上的数相同,并且是5的倍数。
(2)3 5 既是2的倍数, 又是5的倍数。
(3) 既是2的倍数, 又是5的倍数的最小三位数。
5
5
0
1
0
0
下面的说法对吗?说出理由。
(1)一个自然数不是奇数就是偶数。 ( )
(2)偶数都比奇数大。 ( )
(3)个位上是2,4,6,8,0的自然数都是偶数。 ( )
(4)一个数是2的倍数,那么它一定是偶数。 ( )
(5)能被2,5整除的数个位上的数字一定是0。 ( )
√
×
√
√
√
【选自教材P11 练习三 第5题】
在□里填一个数字,使组成的每个数都是3的倍数。各有几种填法?
□7 4□2 □44 65□ 12□1
2
5
8
0
3
6
9
1
4
7
1
4
7
2
5
8
辩一辩。(对的画“√”,错的画“×”)
1.因为33,36,39,63,69,156这些数都是3的倍数,所以个位
上是3,6,9的数一定是3的倍数。
2.用4,5,6这三个数字,无论怎样排列成没有重复数字
的三位数,一定是3的倍数。
3.3的倍数一定是奇数。
4.一个数是6的倍数,就一定是2,3的倍数。
( )
( )
( )
( )
×
√
×
√
(1)既是2和5的倍数,又是3的倍数的最小两位
数是 。
(2)既是2的倍数,又是3的倍数的最小三位数
是 ,最大三位数是 。
30
102
996
【见教材P13 练习三 第12题】
个位是0
(十位+个位)是3的最小倍数
个位是0,2,4,6,8
百位+十位+个位=3
“一五,一十,十五,二十……”这样数数,数出来的数都是_____的倍数,第12个数是______。
5
60
100,98,96,94,…,8,6,4,2。这些数中的每个数都是____的倍数,其中第15个数是____。
2
72
(1)
(2)
五、自主练习
【见教材P11 练习三 第6题】
在 里填一个数字,使组成的每个数既是2和3的倍数,
又是5的倍数。
6
15
3 0
40
5 0
60
0
0
0
3
6
9
2
5
8
1
4
7
3
6
9
填一填。
1.在12,14,16,32,124,640,6中,是4的倍数的有
( )。
2.既是3的倍数,又是5的倍数的最小三位数是( ),
同时是2,3,5的倍数的最小三位数是( ),
最大三位数是( )。
12,16,32,124,640
105
120
990
一个四位数417 。
(1)要使它是偶数, 里可以填( )。
(2)要使它是3的倍数, 里可以填( )。
(3)要使它既有因数2,又有因数5, 里可以填( )。
0,2,4,6,8
0,3,6,9
0
1有几个因数?
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
质数
合数
1
2,3,5,7,11,13,17,19
4,6,8,9,10,12,
14,15,16,18,20
1(既不是质数
也不是合数)
非零自然数按照因数的个数可以分为几类?
非0自然数
判断下面的说法是否正确,并说一说你的理由。
(1)所有的奇数都是质数。
【选自教材P16 练习四 第1题】
(2)所有的偶数都是合数。
(3)在1,2,3,4,5,…中,除了质数以外都是合数。
(4)两个质数的和是偶数。
不正确,如9是奇数又是合数。
不正确,如2是偶数又是质数。
不正确,1既不是质数又不是合数。
不正确,举例:质数2和3,2+3=5,5是奇数。
我们两个的和是10。
我们两个的积是21。
我们两个的和是20。
我们两个的积是91。
我是最小的质数。
我是最小的合数。
3和7
13和7
2和4
你知道下面的数各是多少吗?
【选自教材P16 练习四 第3题】
1.所有的质数都是奇数,所有的合数都是偶数。
2.自然数可分为奇数和偶数,也可以分为质数和合数。
3. 91是奇数,也是合数。
4.除0和2以外,所有的偶数都是合数。
5.质数加质数的和一定是合数。
辨一辨。(对的画“√”, 错的画“×”)
( )
( )
( )
( )
( )
×
×
√
×
√
选一选。(将正确答案的序号填在括号里)
1.一个合数至少有( )个因数。
A.2 B. 3 C.4
2.10以内既是奇数又是合数的数有( )个。
A.0 B.1 C.2
B
B
质数与质数的积( )。
A.一定是合数
B.一定是质数
C.可能是质数,也可能是合数
A
两个自然数相加,和的奇偶性我们可以确定,如果是多个自然数相加呢?
(1)偶数+偶数+偶数+······+偶数
(2)奇数+奇数+奇数+······+奇数
=
偶数
①奇数个奇数相加,和是奇数;
②偶数个奇数相加,和是偶数。
1+2+3+4+……+98+99 ,如果不计算,你能很快说出这道算式的和是奇数还是偶数吗?
偶数个奇数的和是偶数,其它偶数的和也是偶数,
所以1+2+3+4+······+98+99的和是偶数。
1+2+3+4+……+98+99
50个奇数
不计算,直接判断结果是奇数还是偶数。
46 + 27( ) 34 + 108 ( )
13×72 ( ) 268 × 54 ( )
89 +415 ( ) 71 × 67 ( )
奇数
奇数
偶数
偶数
偶数
偶数
结合图形抽象出面、棱、顶点。
面
棱
(面和面相交的线段)
顶点
(棱和棱的交点)
三、长方体和正方体
①认识长方体的长、宽、高。
长
宽
高
相交于同一顶点的3条棱的长度分别叫作长方体的长、宽、高。
长方体的长、宽、高是相对的,
左右竖着的棱称为高,
左右横着的棱称为宽。
一般把前后横着的棱称为长,
三、长方体和正方体
长方体和正方体的特征:
形体 相同点 不同点 联系
面 棱 顶点 面的形状 面的面积 棱长
长方体
正方体
6
个
12
条
8
个
6个面都是长方形。(特殊情况有两个相对的面是正方形)
6个面都是正方形
相对的两个面的面积相等
6个面的面积都相等
相对的棱的长度相等
12条棱的长度都相等
正方体是一种特殊的长方体
三、长方体与正方体
表面积 体积 容积
意义
计算 方法
常用计量单位
单位间进率
长方体或正方体6个面的总面积
物体所占空间的大小
容器所能容纳物体体积的大小
S长=2ab+2ah+2bh
=(ab+ah+bh) ×2
S正=a2×6
V长= abh
V正= a3
V=sh
长方体、正方体的意义、表面积、体积及容积
m 、dm 、cm
m 、 dm 、cm
m 、 dm 、 cm
、L 、 ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
1L=1000ml
1dm =1L
1cm =1ml
同体积
(从里面量)
三、长方体和正方体
(三)如何计算不规则物体的体积?
判断哪组的小棒可以搭成长方体。
小棒长度 ① ② ③
15cm 5根 4根 8根
10cm 4根 4根 0根
8cm 3根 4根 4根
三、长方体和正方体
算出下图中长方体的棱长和。
(长+宽+高)×4
三、长方体和正方体
(10+4+6)×4
=20×4
=80(cm)
(3+7+3)×4
=13×4
=52(cm)
三、长方体和正方体
6个面,相对的两个面完全相同。
12条棱,相对的棱长度相等。
8个顶点。
长
宽
高
长方体的特征
三、长方体和正方体
一个长、宽、高分别为 40 cm、30 cm、20 cm 的
小纸箱,在所有的棱上粘上一圈胶带,至少需要
多长的胶带?
20×4+30×4+40×4=360(cm)
【选自教材P21 练习五 第2题】
或(20+30+40)×4=360(cm)
答:至少需要360cm 的胶带。
三、长方体和正方体
选一选。 (将正确答案的序号填在括号里)
长方体有( )个顶点,( )个面,( )个棱。
A.6 B.8 C.12
B
1.
A
C
长方体中有( )组相对的面的面积分别相等。
A.3 B.2 C.1
A
2.
三、长方体和正方体
用一根长 60 cm 的铁丝正好可以焊接一个长 6 cm,宽 5 cm,高( )cm 的长方体框架。
A.4 B.16 C.8
A
三、长方体和正方体
(1)正方体的6个面 。
(2)正方体的12条棱 。
完全相同
长度相等
三、长方体和正方体
正方体有12条棱,每条棱的长度相等,所以棱长和=棱长×12。
三、长方体和正方体
判断:长方体的6个面一定都是长方形。 ( )
长方体的6个面一般是长方形,但特殊情况下有两个相对的面是正方形。
×
三、长方体和正方体
一个正方体的棱长是3厘米,那么这个正方体的棱长总和是多少厘米?
3×12=36(厘米)
答:这个正方体的棱长总和是36厘米。
棱长总和=棱长×12
三、长方体和正方体
正方体
立方体
6个面完全相同。
8个顶点。
12条棱长度相等。
正方体的特征
正方体可以看成是长、宽、高都相等的长方体。
三、长方体和正方体
90×2+55×2+22×4=378(m)
答:工人叔叔至少需378m的彩灯线。
为迎接“五一”国际劳动节,工人叔叔要在礼堂的四周装上彩灯(地面的四边不装)。已知礼堂长90m,宽55m,高22m,工人叔叔至少需要多长的彩灯线?
【选自教材P21 练习五 第5题】
三、长方体和正方体
用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?
8×12÷4-(10+7)
=96÷4-17
=24-17
=7(厘米)
答:它的高应该是7厘米。
三、长方体和正方体
正方体的全部展开图
“一四一型”
“二三一型”
“三三型”
“二二二型”
( )
√
( )
√
( )
折叠后,下面哪些图形能围成左侧的正方体?在括号里画“√”。
【选自教材P23 做一做】
注意:任何正方体的展开图不能是“田字型”,也不能是“凹字型”。
三、长方体和正方体
长方体或正方体 6 个面的面积之和,叫作它的表面积。
用自己的话说一说什么叫做长方体或者正方体的表面积
三、长方体和正方体
长方体的表面积= 长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
a
b
c
S表= 2(ab+ah+bh)
三、长方体和正方体
正方体的表面积的计算方法是怎样的?
正方体的表面积= 棱长×棱长×6
a
S表=6a2
三、长方体和正方体
将下面的展开图围成正方体后,哪两个面分别相对?
春对______
秋对______
暮鼓对______
夏
冬
晨钟
【选自教材P25 练习六 第2题】
三、长方体和正方体
做一个长 5dm,宽 4dm,高 3dm的长方体布艺收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
= 47×2
= 94(dm2)
答:至少需要 94 平方分米的布。
【选自教材P25 练习六 第4题】
三、长方体和正方体
一个长0.75m、宽0.5m、高1.6m的简易衣柜需要换布罩
(如右图,没有底面)。至少需要用多少平方米布料?
【选自教材P24 做一做】
(0.75×1.6+0.5×1.6)×2+0.75×0.5
= 2×2+0.375
= 4.375(m2)
答:至少需要用4.375平方米布料。
三、长方体和正方体
长方体或正方体 6 个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S表= 2(ab+ah+bh)
正方体表面积=棱长×棱长×6
S表=6a2
长方体和正方体的表面积
三、长方体和正方体
计算下面长方体和正方体的表面积。
上、下每个面的面积是:___________________
前、后每个面的面积是:___________________
左、右每个面的面积是:___________________
长方体的表面积是:_________________或_____________
20×10=200(cm2)
20×8=160(cm2)
10×8=80(cm2)
200×2+ 160×2+ 80×2=880(cm2)
(200+ 160+ 80)×2=880(cm2)
三、长方体和正方体
每个面的面积是:___________________
正方体的表面积是:_________________
8×8=64(cm2)
64×6=384(cm2)
三、长方体和正方体
一个长方体礼品盒,长 20 cm,宽 12 cm,高 8 cm,如果包装这个礼品盒的用纸是其表面积的 1.2 倍,至少要用多少平方厘米的包装纸?
(20×12+20×8+12×8)×2 =992(cm2)
992×1.2 =1190.4(cm2)
答:至少要用1190.4平方厘米的包装纸。
三、长方体和正方体
下面哪些图形是正方体的展开图?
( )
( )
( )
( )
√
×
√
×
三、长方体和正方体
一个长方体的饼干盒,长 10 cm,宽 6 cm,高 12 cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
10 cm
6 cm
12 cm
分析:商标纸的面积是饼干盒前、后、左、
右四个面的面积之和。
【选自教材P25 练习六 第5题】
10×12 ×2+6 ×12 ×2 = 384(cm2)
答:这张商标纸的面积至少有
384平方厘米。
三、长方体和正方体
一个新建的游泳池长 50 m,长是宽的 2 倍,深 2.5 m。现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米的瓷砖?
50 m
25 m
2.5 m
分析:游泳池只有 5 个面。
【选自教材P26 练习六 第10题】
50÷2 = 25(m)
50×25+50×2.5×2+25×2.5×2 =1625( m2 )
答:一共需要贴 1625 平方米的瓷砖。
三、长方体和正方体
把一个棱长46cm的正方体纸箱各面都贴上红纸,作为捐款箱。
(1)至少需要多少平方厘米的红纸?
(开口处忽略不计)
(2)如果只在棱上粘贴一圈胶带纸,
一卷4.5m长的胶带纸够用吗?
【选自教材P25 练习六 第6题】
(1)46×46×6=12696(cm2)
(2)46×12=552(cm)=5.52m
5.52m>4.5m
答:(1)至少需要12696cm2的红纸。(2)不够用。
三、长方体和正方体
一个正方体玻璃鱼缸的棱长为3dm,制作这个鱼缸至少需要多少平方分米的玻璃?(上面没有盖。)
3×3×5=45(dm2)
答:至少需要玻璃45dm2。
【选自教材P26 练习六 第8题】
三、长方体和正方体
一个正方体礼品盒的棱长为1.2dm。如果包装这个礼品盒的用纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
1.2×1.2×6=8.64(dm2)
8.64×1.5=12.96(dm2)
答:至少要用12.96dm2的包装纸。
【选自教材P26 练习六 第9题】
三、长方体和正方体
学校要粉刷教室。已知教室的长是8m,宽是6m,高是3m,门窗的面积是11.4m2。如果每平方米需要花6元涂料费,粉刷这个教室需要多少涂料费?
8×6+8×3×2+6×3×2-11.4=120.6(m2)
120.6×6=723.6(元)
答:粉刷这个教室要花费723.6元。
【选自教材P26 练习六 第11题】
三、长方体和正方体
如何把右面这个长方体木块分成两个棱长为4cm的正方体?这两个正方体的表面积之和与原长方体的表面积相等吗?
表面积不相等。
【选自教材P26 练习六 第13题】
三、长方体和正方体
橡皮的体积约是 10____
电饭锅的体积约是 25____
集装箱的体积约是 40____
m3
dm3
cm3
【选自教材P32 练习七 第3题】
在横线上填写合适的体积单位。
三、长方体和正方体
下面是用棱长 1 cm 的小正方体拼成的几何体,它们的体积各是多少?
9cm3
8cm3
6cm3
4cm3
【选自教材P28 做一做 第2题】
三、长方体和正方体
填一填。
物体所占( )的大小叫做物体的体积,计量体积常用的单位有( )、( )和
( ),用字母表示是( )、( )和( )。
空间
立方厘米
立方分米
立方米
cm3
dm3
m3
三、长方体和正方体
棱长是( )的正方体的体积是 1 cm3;
棱长是( )的正方体的体积是 1 dm3 ;
棱长是( )的正方体的体积是 1 m3 。
1 cm
1 dm
1 m
厘米是用来计量( )的单位。
平方厘米是用来计量( )的单位。
立方厘米 是用来计量( )的单位。
长度
面积
体积
三、长方体和正方体
在括号里填出合适的体积单位。
一个抽纸盒的体积约为 2( )
一个牙膏盒的体积约为 480( )
dm3
cm3
三、长方体和正方体
一节火车车厢的体积约为 250( )
一本故事书的体积约为 300( )
m3
cm3
三、长方体和正方体
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=abh
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
三、长方体和正方体
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫作底面积。
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
三、长方体和正方体
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=abh
=15×7×5
=525(cm3)
答:它的体积是525cm3。
【选自教材P31 做一做 第1题】
三、长方体和正方体
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
三、长方体和正方体
把下表中长方体或正方体的相关数据补充完整。
512 m3
15 cm
52 dm2
三、长方体和正方体
算一算。
43=______
4×3=______
4+4+4=______
82=______
8×2=______
8+8=______
64
12
12
64
16
16
【选自教材P32 练习七 第6题】
三、长方体和正方体
【选自教材P33 练习七 第7题】
16×5×10=800(m3)
9×9×9=729(dm3)
3×3×10=90(cm3)
三、长方体和正方体
50cm=0.5m
50×30×0.5=750(m3)=750(方)
要在平地挖一个长 50 m、宽 30 m、深50 cm 的长方体土坑,一共要挖出多少方的土?
在工程上,土、沙、石等的体积常用“方”作单位,1方=1立方米。
【选自教材P33 练习七 第8题】
三、长方体和正方体
30×30×30=27000(cm3)
一块棱长 30 cm 的正方体冰块,它的体积是多少立方厘米?
【选自教材P33 练习七 第9题】
三、长方体和正方体
【选自教材P33 练习七 第10题】
14cm
200dm3
81m2
378cm3
三、长方体和正方体
2.4dm2=0.024m2
0.024×3×500=36(m3)=36(立方米)
答:这些方木一共是36平方米。
【选自教材P33 练习七 第11题】
三、长方体和正方体
单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
下面是我们学过的计量单位,请把下表补充完整。
3.5 dm3=_____cm3
700 dm3=_____m3
3500
0.7
0.25 m3=_______cm3
250000
×1000
÷1000
×1000
×1000
三、长方体和正方体
要砌一面长 15 m、厚 24 cm、高 3 m 的砖墙,如果每立方米用砖 525 块,至少要用砖多少块?
24 cm=0.24 m
V =abh
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:至少要用砖5670块。
【选自教材P35 做一做 第2题】
三、长方体和正方体
1.02 m3=______dm3
960 dm3=______m3
6270 cm2=_____dm2
36000 cm3=_____m3
8.63 m2=______dm2
23 dm3=_______cm3
1020
0.96
62.7
0.036
863
23000
【选自教材P36 练习八 第1题】
三、长方体和正方体
一个无盖的鱼缸,长 1.2 m,宽 80 cm,高 6 dm,这个鱼缸可以放多少立方分米的水?
1.2 m=12 dm 80 cm=8 dm
V = abh
=12×8×6
=576(dm3)
答:这个鱼缸可以放 576 dm3 的水。
三、长方体和正方体
辨一辨。 (对的画“√”,错的画“ ”)
1.体积单位间的进率是 1000。
2.1000个1 cm3的小正方体拼成的几何体的
体积是1 dm3。
( )
( )
√
三、长方体和正方体
3.棱长是 1 m 的大正方体可以切成 1000 个
棱长是 1 cm 的小正方体。
4.棱长为 6 cm 的正方体,它的表面积和
体积相等。
( )
( )
三、长方体和正方体
要在一块长25 m、宽9m的长方形地面上铺一层6 cm厚的沙土。一辆车每次能运送1.5 m3的沙土,所需的沙土至少需要用这辆车运送多少次
25×9×0.06 = 13.5(m3)
6 cm=0.06 m
13.5÷1.5 = 9(次)
答:至少需要用这辆车运送9次。
三、长方体和正方体
一个长方体包装盒,从里面量长 28 cm,宽 20 cm,里面的体积为 11.76 dm3。用它装一件长 25 cm、宽 16 cm、高 18 cm 的玻璃器皿,是否装得进去?说一说你的理由。
11.76 dm =11760 cm
11760÷(28×20)=21(cm)
21>18,可以装下。
【选自教材P36 练习八 第2题】
三、长方体和正方体
(100×45×4.5+45×5×35×2)×50
=1800000(cm3)
=1.8(m3)=1.8(方)
答:做这些凳子至少用了1.8方混凝土。
某小区新安装了50个混凝土凳子(如右图所示)。凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了多少方混凝土?
【选自教材P36 练习八 第3题】
三、长方体和正方体
“六一”儿童节前,小学生用棱长 3 cm的正方体塑料拼插积木在广场中央搭起了一面长 6 m、高 2.7 m、厚 6 cm 的心愿墙。这面墙一共用了多少块积木?
6m=600cm 2.7m=270cm
600×270×6÷(3×3×3)
=36000(块)
答:这面墙一共用了36000块积木。
【选自教材P36 练习八 第4题】
三、长方体和正方体
一个长方体的无盖玻璃水族箱,长是 6 m,宽是 60 cm,高是 1.5 m。制作这个水族箱需要用多少平方米的玻璃?它的体积是多少?
【选自教材P36 练习八 第5题】
三、长方体和正方体
60 cm=0.6 m
需要玻璃:6×0.6+(6×1.5+0.6×1.5)×2
=23.4(m2)
体积:6×0.6×1.5=5.4(m3)
答:制作这个水族箱需要用23.4m2的玻璃,它的体积是5.4m3。
38 dm=3.8 m
7.6÷(5×3.8)=0.4(m)
将 7.6 m3 的沙子铺在一个长 5 m、宽 38 dm 的沙坑里,可以铺多厚?
答:可以铺0.4m厚。
【选自教材P37 练习八 第6题】
三、长方体和正方体
修建长城所用的某块砖的尺寸如右图所示。这块长城砖的体积是多少?
【选自教材P36 练习八 第8题】
40×10×20=8000(cm3)
答:这块长城砖的体积是8000 cm3 。
三、长方体和正方体
一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是 6 cm、4 cm、5 cm,正方体的棱长是多少厘米?它们的体积相等吗?
【选自教材P37 练习八 第9题】
正方体的棱长:(6+4+5)÷3 = 5(dm),
体积是 5 × 5 × 5 = 125(dm3)
长方体的体积是 6 × 4 × 5 = 120(dm3),
所以长方体和正方体的体积不相等,正方体的体积大。
三、长方体和正方体
茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
最多 6 盒,竖着放 4 盒,横着放 2 盒。
30×30×30÷(20×20×10)=6.75(盒)
【选自教材P37 练习八 第10题】
三、长方体和正方体
判断对错。
(1)一辆货车车厢所能容纳货物的体积,就是
这辆货车车厢的容积。 ( )
(2)一个药瓶里装了半瓶药水,这些药水的体
积就是药瓶的容积。 ( )
(3)有两个体积一样大的箱子,它们的容积一
定同样大。 ( )
√
×
×
三、长方体和正方体
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
三、长方体和正方体
一个长方体的油箱,从里面量长 5 dm,宽 4 dm,高 2 dm。这个油箱可以装多少升油?
5×4×2=40(dm3)
40 dm3=40 L
答: 这个油箱可以装汽油 40 L。
三、长方体和正方体
在横线上填写合适的容积单位。
一瓶墨水约 50____
一瓶洗手液约500___
“奋斗者”号载人潜水器载人舱的容积为3___
mL
mL
一台冰箱容积约229___
m3
L
【选自教材P40 练习九 第1题】
三、长方体和正方体
4 L=______mL 82 cm3=_____mL 4800 mL=_____L
2.4 L=______mL 35 dm3=______mL
500 mL=_____L
8.04 dm3=_____L=_______mL
785 mL=_____cm3=______dm3
4000
4.8
82
0.5
35000
2400
8.04
8040
785
0.785
【选自教材P40 练习九 第2题】
三、长方体和正方体
一桶 18 L的矿泉水相当于_____瓶 1500 mL 的矿泉水。
12
【选自教材P40 练习九 第3题】
三、长方体和正方体
一种微波炉,产品说明书上标明:炉腔内部尺寸400×225×300(单位:mm)。这个微波炉的容积是多少升?
400 mm=4 dm
225 mm=2.25 dm
300 mm=3 dm
4×2.25×3=27(dm3)
27 dm3=27 L
答:这个微波炉的容积是 27 L。
【选自教材P40 练习九 第4题】
三、长方体和正方体
为解决海岛上淡水缺乏的问题,某驻岛部队和当地居民共同修建了一个长 22 m、宽 10 m、深 1.8 m 的淡水蓄水池。这个蓄水池最多可蓄水多少立方米?
22×10×1.8 = 396(m3)
答:最多可蓄水 396 m3。
【选自教材P40 练习九 第5题】
三、长方体和正方体
一辆货车的车厢是长方体,从里面量长 3 m,宽 2.5 m,高 2 m。车厢的容积是多少立方米?
3×2.5×2=15(m3)
答:它的容积是 15 立方米。
【选自教材P40 练习九 第6题】
三、长方体和正方体
1. 1个水壶能装水2.5 L。“2.5L”指的是这个水壶的
( )。
A.体积 B.表面积 C.容积
2. 一个木箱能容纳40dm3的物体,这个木箱的体积
( )40dm3
A.大于 B.等于 C.小于
C
A
选一选。(将正确答案的序号填在括号里)
三、长方体和正方体
3.两个容器的体积相等,它们的容积( )。
A.可能不相等 B.一定不相等 C.一定相等
4.一个长方体水箱从里面量长0.6 m,宽0.4 m,高0.3m,
这个水箱可以装水( )L。
A.0.027 B.0.72 C.72
C
A
三、长方体和正方体
下图中珊瑚石的体积是多少?
8×8×( 7-6 )=64(cm3)
答:珊瑚石的体积是 64 cm3。
【选自教材P41 练习九 第7题】
三、长方体和正方体
将一块假山石放入一个盛有水的、底面积为 51 dm2 的长方体鱼缸中,完全浸没后,水面上升了 3 cm。这个假山石的体积有多大?
51×0.3=15.3(dm3)
3 cm=0.3 dm
答:假山石的体积为15.3dm3。
【选自教材P41 练习九 第8题】
三、长方体和正方体
在一个长 8 m、宽 5 m、高 2 m 的水池中注满水,然后把两条长 3 m、宽 2 m、高 4 m 的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×(4-2)×2=24(m3)
答:水池溢出的水的体积是 24 m3。
【选自教材P41 练习九 第9题】
三、长方体和正方体
把两个棱长为 1.5 dm 的正方体木块拼成一个长方体。这个长方体的体积、表面积分别是多少?如果是用 3 个正方体木块呢?
体积:1.5×1.5×1.5×2=6.75(dm3)
表面积:1.5×1.5×10=22.5(dm2)
体积:10.125 dm3
表面积:31.5 dm2
【选自教材P41 练习九 第10题】
三、长方体和正方体
右图是新疆吐鲁番酿制葡萄干的一种长方体晾房。其中一间从里面测量的底面积是 24.6 m2,高是 3 m。它的容积是多少呢?
24.6×3=73.8(m3)
答:它的容积是 73.8 m3。
【选自教材P41 练习九 第11题】
三、长方体和正方体
“冰雪大世界”每年用的冰大约能融化成 6 万立方米的水,这相当于多少个长 50 m、宽 25 m、深 1.2 m 的水池的蓄水量?
60000÷(50×25×1.2)= 40(个)
答:相当于 40 个这样的水池的蓄水量。
【选自教材P41 练习九 第12题】
三、长方体和正方体
求下图中大圆球的体积。
【选自教材P41 练习九 第13题】
你读到了哪些信息?要解决什么问题?
1个
+
1个 ,
水溢出12mL,
1个
+
4个 ,
水溢出24mL,
求大球的体积。
三、长方体和正方体
24 mL=24 cm3,12 mL=12 cm3
(24-12) ÷ 3=4(cm3)
12-4=8(cm3)
答:大球的体积是8cm3。
1个
+
1个 ,
水溢出12mL,
1个
+
4个 ,
水溢出24mL,
求大球的体积。
有一个装有一些水的长方体玻璃缸,从里面量长10 cm,宽 8 cm。往这个玻璃缸里放入一个柿子,水面上升了2cm(水淹没柿子且未溢出),这个柿子的体积是多少
10×8×2=160(cm3)
答:柿子的体积是160 cm3。
三、长方体和正方体
一个长方体玻璃容器,从里面量长和宽都是 2 dm ,里面
装有 5.6 L水, 将一个鹅卵石完全浸没在水中,水未溢出,
这时水深15 cm,这个鹅卵石的体积是多少?
5.6 L=5.6 dm3
15 cm=1.5 dm
2×2×1.5-5.6=0.4(dm3)
答:这个鹅卵石的体积是0.4 dm3。
三、长方体和正方体
求下图中一个小球的体积。(小球体积均相等)
20×16×(16-14)÷(6-1)=128(cm3)
答:小球的体积是128cm3。
三、长方体和正方体
长方体的长、宽、高都变为原来的 2 倍,它的表面积和体积分别发生了什么变化?你发现了什么规律?
长方体 长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
1 2 1 3
2 4 2 6
3 8 4 12
22
6
88
48
352
384
规律:如果长方体长、宽、高都变为原来的 2 倍,
它的表面积变为原来的 4 倍,体积变为原来的 8 倍。
【选自教材P43 练习十 第2题】
三、长方体和正方体
8×4.5×2 = 72(m3)
一个长方体鱼塘长 8 m,宽 4.5 m,深 2 m。这个鱼塘的容积是多少?
答:这个鱼塘的容积是72立方米。
【选自教材P43 练习十 第3题】
三、长方体和正方体
某古建筑景点定做了 25 个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米 18 元,这些宫灯的外饰面一共要花多少钱?
(66×20×4+46×80×4)×25
= 500000(cm2)
= 50(m2)
18×50 = 900(元)
答:这些宫灯的外饰面一共要花900元。
【选自教材P43 练习十 第4题】
三、长方体和正方体
选一选。(将正确答案的序号填在括号里)
1. 堆一个体积是1m3的大正方体,需要用体积是
1dm3的正方体木块( )个。
A.10 B.100 C.1000
C
三、长方体和正方体
2.一大桶矿泉水的净含量为 18 L ,相当于( )
瓶 600 mL 的小瓶矿泉水。
A.300 B.30 C.3
B
三、长方体和正方体
3. 一个正方体的棱长扩大到原来的 2 倍后体积
是 64 dm3 ,原来正方体的体积是( )dm3。
A.32 B.16 C.8
C
三、长方体和正方体
4.将两个长10 dm 、宽8 dm 、高5 dm 的长方体货
物包装在一起,至少要用( )dm2的包装纸。
A.520 B.600 C.680
A
三、长方体和正方体
修路队要给一段长200 m,宽18 m的水泥路面铺一层6cm厚的沥青,一共需要沥青多少方
(1方=1 m3)
6 cm = 0.06 m
200×18×0.06 = 216(m3)
216 m3= 216 方
答:一共需要沥青 216 方。
三、长方体和正方体
(1)(50×30+40×30)×2+50×40=7 400(平方厘米)。
答:需要玻璃7 400平方厘米。
(2)40升=40 000立方厘米,40 000÷(50×40)=20(厘米)。
答:水深大约20厘米。
(3)50×40×2.5=5 000(立方厘米)。
答:放入物体的体积一共是5 000立方厘米。
一个长方体玻璃鱼缸,长50厘米、宽40厘米、高30厘米。
(1)做这个鱼缸至少需要玻璃多少平方厘米?
(2)在鱼缸里注入40升水,水深大约多少厘米?
(3)再往水里放入鹅卵石、水草和鱼,测得水面上升了2.5厘米,求放入物体的体积一共是多少立方厘米?
三、长方体和正方体
一个长方体的容器(如图),里面的水深5 cm,把这个容器盖紧后竖放,使长10 cm、宽8 cm的面朝下,这时里面的水深是多少厘米?
20×10×5÷(10×8)
=12.5(厘米)。
答:这时里面的水深是12.5厘米。
三、长方体和正方体
2
3
分子:
表示取其中的几份。
分数线:
表示平均分。
分母:
表示平均分的份数。
四、分数的意义和性质
的分数单位是( ),
的分数单位是( )。
的分数单位是( ),
的分数单位是( ),
分母是几,分数单位就是几分之一。
四、分数的意义和性质
的分数单位是( ),
的分数单位是( ),
的分数单位是( ),
的分数单位是( ),
有( )个分数单位;
有( )个分数单位;
有( )个分数单位;
有( )个分数单位。
分子是几,就有几个分数单位。
1
2
3
5
四、分数的意义和性质
把下面每个图形都看作单位“1”,用分数表示各图中涂色部分的大小。
【选自课本P47 做一做 第1题】
四、分数的意义和性质
每个福娃是这排福娃的 。
2个冰墩墩是这排冰墩墩的 。
1
5
【选自课本P47 做一做 第2题】
2
5
四、分数的意义和性质
每个茶杯是这套茶杯的
每种颜色的跳棋是这盒跳棋的 。
一小杯液体是这瓶液体的
1
4
1
6
1
10
【选自课本P47 做一做 第3题】
四、分数的意义和性质
填一填。
1. 表示把单位“1”平均分成( )份,取其中
的( )份,它的分数单位是( )。
7
6
2. 4个 是( ),1里面有( )个 。
8
四、分数的意义和性质
把下面每个图形都看作单位“1”,用分数表示各图中涂色部分的大小。
8
3
7
5
4
3
8
5
四、分数的意义和性质
每个苹果是这些苹果的 。
5
1
每块饼干是这些
饼干的 。
8
1
四、分数的意义和性质
3盆鸡蛋是这些鸡蛋的 。
吃了的梨是这些梨的 。
4
3
6
2
四、分数的意义和性质
一盒蛋糕有12个(如图),
如果平均分给6个小朋友,
每人分得这盒蛋糕的 ,每人分得( )个;
如果平均分给2个小朋友,
每人分得这盒蛋糕的 ,每人分得( )个。
6
1
2
2
1
6
四、分数的意义和性质
按要求涂色。
涂上红色,其余的 涂上你喜欢的颜色。
2
3
涂上绿色,其余的 涂上你喜欢的颜色。
1
2
【选自课本P48 练习十一 第1题】
四、分数的意义和性质
1
3
4
一包饼干平均分给3人,每人分得 包。如果一包有12块,平均每人分得( )块。
【选自课本P48 练习十一 第2题】
四、分数的意义和性质
读出下面的分数,并写出每个分数的分数单位及分数单位的个数。
分 数:
分 数 单 位:
分数单位的个数:
( )个
( )个
( )个
( )个
( )个
1
6
1
7
1
2
1
15
4
1
18
11
1
100
7
【选自课本P48 练习十一 第3题】
四、分数的意义和性质
上面两条直线中,每条直线上的最小刻度用分数表示分别是多少 它们分别是哪些分数的分数单位
0
1
0
1
用直线上的点表示下面各分数。
【选自课本P48 练习十一 第4题】
四、分数的意义和性质
0
1
0
1
(1)最小刻度是 ,是 , , 的分数单位。
1
4
1
4
2
4
3
4
(2)最小刻度是 ,是 , , , , 的分数单位。
1
6
1
6
2
6
3
6
4
6
5
6
用直线上的点表示下面各分数。
【选自课本P48 练习十一 第4题】
四、分数的意义和性质
(1)5个 组成( ), 由( )个
组成。
四、分数的意义和性质
(2)8个 组成1, 1里面有12个 。
1
8
12
填一填。
1. 地球陆地面积约地球总面积的 ,这里是把
( )看作单位“1”。
读作( ),它的分数
单位是( )。
地球总面积
一百分之二十九
四、分数的意义和性质
2. 里面有( )个 ,4个 是( ),
是3个( )。
7
3. 里面有( )个 分数单位 ,再添上( )
个这样的分数单位就是“1”。
3
5
选一选。(将正确答案的序号填在括号里)
1.下面的分数中,分数单位最小的是( )。
A.
B.
C.
D.
D
四、分数的意义和性质
2.把7个苹果平均分给4个小朋友,每个小朋友分
得这些苹果的( )。
A.
B.
C.
D.
C
填表。
3
7
4
7
63
四、分数的意义和性质
(1)把2个月饼平均分给3
人,每人分多少个?
(2)把5个月饼平均分给8人,
每人分多少个?
2÷3= (个)
5÷8= (个)
四、分数的意义和性质
被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线。
被除数
÷
除数
=
被除数
除数
除法是
一种运算
分数是一种数
a
÷
b
=
a
b
(b≠0)
相当于
相当于
相当于
分数与除法的关系
用分数表示下面各式的商。
24÷25= 16÷49=
2÷9= 11÷12=
【选自课本P51 练习十二 第3题】
四、分数的意义和性质
在括号里填上适当的数。
7÷13= =( )÷( )
( )÷7=
13
7
8
5
4
【选自课本P50 做一做 第1题】
四、分数的意义和性质
1kg葡萄干平均装在2个袋子里,每袋装多少千克?平均装在3个袋子里呢?(用分数表示。)
1÷2 = (kg)
1
2
1÷3 = (kg)
1
3
答:装2个袋子,每袋重 kg,装3个袋子,每袋重 kg。
【选自课本P51 练习十二 第1题】
四、分数的意义和性质
3÷4 = (m )
3
4
3÷5 = (m )
3
5
答:种4种花,每种花平均占地 平方米,种5种花,每种花平均占地 平方米。
3
4
3
5
一个3m2的花坛,种4种花,每种花平均占地多少平方米 种5种呢 (用分数表示。)
【选自课本P51 练习十二 第2题】
四、分数的意义和性质
填一填。
1.
7÷8=
( )
( )
( )÷9=
=( )÷( )
( )÷( )=
7
8
4
7
37
13
45
四、分数的意义和性质
2.
km表示把4 km平均分成( )份,取其中的
( )份,即 km;
也可以表示把1km平均分成( )份,取其中的
( )份,即 km。
( )
( )
( )
( )
9
1
9
4
9
4
9
4
四、分数的意义和性质
5
10
32
100
23
60
17
60
3.
四、分数的意义和性质
7
100
57
1000
500
1000
1
1000
四、分数的意义和性质
把一根2 m长的绳子平均分成5段,每段长多少米?平均分成6段呢?(用分数表示。)
2÷5=
(m)
2÷6=
(m)
答:平均分成5段,每段长 米,
平均分成6段,每段长 米。
四、分数的意义和性质
7 dm =
( )
( )
m
9
10
30
10
133
1000
7
10
56
100
53
1000
23
1000
13
60
48
100
9 cm =
( )
( )
dm
30 cm =
( )
( )
dm
133 dm =
( )
( )
m3
56 cm =
( )
( )
dm
53 mL =
( )
( )
L
23 kg =
( )
( )
t
13 秒 =
( )
( )
分
48 公顷 =
( )
( )
平方千米
【选课课本P51 练习十二 第4题】
动物园里有大象9头,金丝猴4只。金丝猴的数量是大象的几分之几?
答:金丝猴的数量是大象的 。
【选课课本P50 做一做 第2题】
四、分数的意义和性质
81个月球和1个地球的质量相等。月球质量是地球质量的几分之几?
【选课课本P51 练习十二 第5题】
答:月球的质量是地球质量的 。
1
81
四、分数的意义和性质
4月23日是世界读书日。这一天,标价11元一本的《快乐数学》售价9元。
(1)这本书的售价是标价的几分之几?
答:这本书的售价是标价的 。
9
11
【选课课本P52 练习十二 第10题】
四、分数的意义和性质
问题:优惠的价格占原来标价的几分之几?
解答:11-9=2(元) 2÷11=
2
11
(2)你还能提出其他数学问题并解答吗?
4月23日是世界读书日。这一天,标价11元一本的《快乐数学》售价9元。
【选课课本P52 练习十二 第10题】
四、分数的意义和性质
五(1)班共有17幅书法作品参加学校的书法比赛,其中4幅作品从全校255幅参赛作品中脱颖而出获奖。
(1)五(1)班获奖作品占全班参赛作品的几分之几
(2)五( 1 )班参赛作品占全校参赛作品的几分之几
两小题中的单位“1”
分别是什么
【选课课本P52 练习十二 第11题】
四、分数的意义和性质
(1)单位“1”是全班的参赛作品。
4
17
4
÷
17
=
(2)单位“1”是全校的参赛作品。
17
255
17
÷
255
=
填空。
(1) 年有( )个月, 年有( )个月。
(2) 一年中,大月的月份占 ,小月的月份占
。
(3) 一个星期中,周六、周天两天占一周的 。
6
9
7
12
2
7
【选课课本P52 练习十二 第13题】
4
12
四、分数的意义和性质
1÷5 =
1
5
答:桌子的宽度是这颗纺锤树最粗部分直径的 。
1
5
一棵纺锤树最粗部分的直径为5m,一张桌子的宽为1 m。桌子的宽度是这棵纺锤树最粗部分直径的几分之几
纺锤树的根系发达,树干里可以贮存很多水分。
四、分数的意义和性质
50+25 = 75(头)
16÷75 =
25
50
某农场有50头大牛和25头小牛,还有16只羊。
(1)大牛的头数是小牛的多少倍?
(2)小牛的头数是大牛的几分之几?
(3)你还能提出其他数学问题并解答吗?
(1)50÷25 = 2
(3)羊的只数是牛的几分之几?
(2)25÷50 =
25
50
(提问不唯一)
四、分数的意义和性质
5÷6 = (m)
5
6
答:平均每人分 米。
5
6
老师买了5m的红绸带,平均分给表演节目的6名女生。每人分得几米?(用分数表示)
四、分数的意义和性质
1÷15 = (km)
1
15
答:平均每分钟走 千米。
1
15
小明15分钟走了1km的路,平均每分钟走多少千米?(用分数表示。)
四、分数的意义和性质
带分数
分数
真分数
假分数
<1
≥1
, ,
···
, ,
···
,
···
(分子<分母)
(分子≥分母)
(分子不是分母的整数倍)
分子比分母小的分数叫作真分数,真分数小于1。
单位“1”
单位“1”
单位“1”
<1
<1
<1
四、分数的意义和性质
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
=1
>1
>1
分子大于或等于分母的分数叫作假分数,
假分数大于或等于1。
四、分数的意义和性质
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
1
2
+
+
读作:
“二又五分之一”
读作:
“一又四分之三”
像这样由整数和真分数合成的数叫作带分数。
由几个圆组成?
由几个圆组成?
2
0
1
下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
(真)
(真)
(真)
(假)
(假)
(假)
(假)
【选自课本P54 做一做 第1题】
单位“1”
四、分数的意义和性质
判断下面的说法是否正确,并说一说你的理由。
(1)我吃了一个西瓜的 。
(2)爷爷把一块菜地的 种了西红柿, 种了茄子,
种了辣椒。
(3)一块巧克力,我吃了 ,表哥吃了 。
不对
不对
对
【选自课本P55 练习十三 第2题】
四、分数的意义和性质
把一个图形看作单位“1”,用分数表示图中的涂色部分,再读一读。
读作:四分之七
读作:六分之二十三
【选自课本P55 练习十三 第1题】
四、分数的意义和性质
(1)写出分母是7的所有真分数。
(2)写出分子是7的所有假分数。
(1)
1
7
2
7
3
7
4
7
5
7
6
7
(2)
7
1
7
2
7
3
7
4
7
5
7
6
7
7
【选自课本P56 练习十三 第8题】
四、分数的意义和性质
填一填。
1.分数 ,当x( )时,它是真分数;
当x( )时 ,它是大于1的假分数,
当x( )时 ,它是等于1的假分数,
当x( )时, 无意义。
>9
=9
<9
=0
四、分数的意义和性质
2.如果 是真分数, 是假分数,那么n可以取的
数有( )个。
6
四、分数的意义和性质
7÷4=1……3
=
①假分数化成带分数时,分数的大小不变,分数单位也不变,所以真分
数的分母不变。
②如果分子是分母的整数倍,这个假分数表示的就是一个整数;
如果分子不是分母的整数倍,带分数就是整数与真分数合成的数。
四、分数的意义和性质
把下面的假分数化成整数或带分数。
15
8
5
21
50
43
12
69
20
30
15
9
2
7
3
2
7
1
2
1
3
5
5
5
9
3
7
12
3
9
20
【选自课本P54 做一做 第2题】
四、分数的意义和性质
(1) 3个人平均分,每人分 杯,也就是____杯。
(2) 2个人平均分,每人分______杯。
3
3
1
【选自课本P55 练习十三 第3题】
有3杯水。
四、分数的意义和性质
8
5
12
5
15
5
18
5
1
5
1
4
5
2
3
5
3
在直线上面的 里填上适当的假分数,直线下面的 里填上适当的带分数。
【选自课本P55 练习十三 第5题】
四、分数的意义和性质
1
2
3
1
3
2
把一个图形看作单位“1”,用分数表示各图中的涂色部分。
【选自课本P55 练习十三 第6题】
四、分数的意义和性质
<
<
>
=
带分数
在○里填上“>”“<”“=”。
你认为带分数和假分数哪个更容易看出数的大小
【选自课本P56 练习十三 第9题】
四、分数的意义和性质
10÷3= (天)= 3 (天)
10
3
1
3
答:这板药能吃3 天。
1
3
一板药共10粒,每天早、中、晚各吃1粒。这板药能吃多少天 (用带分数表示。)
【选自课本P55 练习十三 第4题】
四、分数的意义和性质
熊的冬眠时间约是睡鼠的几分之几?睡鼠的冬眠时间约是熊的几分之几?
7÷5=
7
5
5÷7=
5
7
【选自课本P56 练习十三 第7题】
5
7
7
5
四、分数的意义和性质
先涂色表示下面的分数,再比较它们的大小。
<
=
四、分数的意义和性质
下面每组中的两个分数是否相等?相等的在括号里画“√”,不相等的画“×”。
和 ( )
和 ( )
和 ( )
和 ( )
√
×
√
×
四、分数的意义和性质
五(1)班 的同学参加舞蹈小组, 的同学参加了书法小组。参加哪个小组的人数多?
2
5
=
2×2
5×2
=
4
10
因为 ,所以参加两个小组的人数相等。
四、分数的意义和性质
下列分数中哪些在直线上能用同一个点表示?把它们在直线上表示出来。
0
1
2
四、分数的意义和性质
把下面的分数化成分母是10而大小不变的分数。
3
2
=
3×5
2×5
=
15
10
6
20
=
6÷2
20÷2
=
3
10
24
30
=
24÷3
30÷3
=
8
10
1
5
=
1×2
5×2
=
2
10
15
50
=
15÷5
50÷5
=
3
10
四、分数的意义和性质
( )
( )
( )
( )
涂色表示出与给定分数相等的分数。
2
6
2
8
四、分数的意义和性质
因为
( )
( )
÷
=
4
10
40
1
所以两个班做练习用的时间一样长。
如果一堂课40分钟,五(1)班做了10分钟的练习,五(2)班做练习的时间占整堂课的 。哪个班做练习用的时间长?
四、分数的意义和性质
布置板报。
哪些栏目的版面一样大?
四、分数的意义和性质
“知识海洋”、“生活乐园”和“科学园地”版面一样大。“历史足迹” 和“开心一刻”一样大。
2021年世界500强企业排行榜中,中国上榜企业数量达145家。中国上榜企业数量占世界500强的 ,也就是 。
29
四、分数的意义和性质
*一个分数的分母不变,分子乘3,这个分数的大小有什么变化?如果分子不变,分母除以5呢?
一个分数的分母不变,分子乘3,这个分数扩大3倍。如果分子不变,分母除以5,这个分数扩大5倍。
四、分数的意义和性质
8的因数
12的因数
1,2,4
3,6,
12
8
1、2、4是8和12公有的因数,叫做它们的公因数。其中,4是最大的公因数,叫做它们的最大公因数。
集合法
四、分数的意义和性质
怎样求 18 和 27 的最大公因数?
列举法
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
18和27的最大公因数是9。
分解质因数
18=2×3×3
27=3×3×3
18和27的最大公因数是9。
求下面各组数的最大公因数。
2和11 9和10
2的因数:1,2
11的因数:1,11
9的因数:1,3,9
10的因数:1,2,5,10
2和11的最大公因数是1
9和10的最大公因数是1
公因数只有1的两个数叫做互质数。
四、分数的意义和性质
18
27
3
6
9
3
2
3
依次用这两个数的公因数去除,直到最后得到的两个商互质为止,然后把公有的质因数相乘就是它们的最大公因数。
短除法
最大公因数乘半边
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用边长是整分米数的正方形地砖将储藏室的地面铺满(使用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
四、分数的意义和性质
男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
【选自课本P63 练习十五 第6题】
四、分数的意义和性质
48 和 36 的最大公因数是 12。
答: 每排最多有 12 人,这时男生有 4 排,女生有 3 排。
48÷12 = 4(排)
36÷12 = 3(排)
每排最多有12人。
在括号里写出各个分数中分子和分母的最大公因数。
( )
( )
( )
( )
( )
( )
1
4
18
3
7
11
【选自课本P63 练习十五 第4题】
四、分数的意义和性质
写出相邻两个数的最大公因数。
1
1
5
3
6
12
36
【选自课本P63 练习十五 第7题】
四、分数的意义和性质
(1)9和16的最大公因数是( )。
A.1 B.3 C.4 D.9
(2)48和60的最大公因数是( )。
A.4 B.6 C.12 D.36
把正确答案的序号填在括号里。
C
A
【选自课本P64 练习十五 第9题】
四、分数的意义和性质
(3)甲数是乙数的倍数,甲、乙两数的最大公因数是( )。
A.1 B.甲数 C.乙数 D.甲、乙两数的积
C
(1)两个数都是质数: ____ 和 ____。
(2)两个数都是合数: ____ 和 ____。
(3) 一个质数一个合数: ____ 和 ____。
按要求写出两个数,使它们的最大公因数是 1。
2
5
4
9
13
8
【选自课本P64 练习十五 第8题】
四、分数的意义和性质
有一张长方形纸,长70cm,宽50cm。如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?
10cm
【选自课本P63 练习十五 第5题】
四、分数的意义和性质
要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米?
12、16 和 44 的最大公因数是 4 。
答: 每根小棒最长是 4 厘米。
【选自课本P64 练习十五 第11题】
四、分数的意义和性质
五(3)班同学买了64个苹果和96个梨去看望养老院的老人。这些水果正好可以平均分给养老院的老人,每人分得的苹果同样多,分得的梨也同样多,且都没有剩余。这个养老院最多有多少位老人
64和96的最大公因数是32,故这个养老院最多有32位老人。
四、分数的意义和性质
把一块长42 m,宽28 m 的长方形菜园划分成若干个面积相等的小正方形。小正方形的面积最大是多少
42和28的最大公因数是14,要使小正方形的面积最大,则边长应为14 m。
14 ×14=196(m2 )
四、分数的意义和性质
填空。
(1)10和15的公因数有 。
1、5
(2)14和49的公因数有 。
1、7
四、分数的意义和性质
找出下面每组数的最大公因数。
6和9 15和12 42和54
30和45 99和36 5和9
34和17 16和48 15和16
13和78
3
3
6
15
9
1
17
16
1
13
四、分数的意义和性质
(1)8和16的公因数有____________,最大因数是________。
(2)8和20的公因数有____________,最大因数是________。
(3)16和20的公因数有____________,最大因数是________。
(4)8、16和20的公因数有_________,最大因数是________。
1、2、4、8
8
1、2、4
4
1、2、4
4
1、2、4
4
四、分数的意义和性质
填空
16
32
( )
16
4
( )
=
=
=
( )
4
1
( )
=
( )
9
10
( )
=
=
( )
24
20
( )
=
=
2
3
8
8
2
2
6
15
16
30
四、分数的意义和性质
24
30
=
24÷2
30÷2
=
12
15
12
15
=
12÷3
15÷3
=
4
5
÷
÷
24
30
=
24 ( )
30 ( )
=
( )
( )
4
5
6
6
像这样,把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
四、分数的意义和性质
像 这样,分子和分母只有公因数1的分数叫做最简分数。
4
5
约分时,通常要约成最简分数。
仔细观察 ,它们之间有什么关系?
四、分数的意义和性质
9
9
4
2
4
1
3
5
下列分数中哪些是最简分数?把不是最简分数的化为最简分数。
、
、
、
、
是最简分数。
【选自课本P65 做一做 第1题】
四、分数的意义和性质
把上下两行相等的两个分数用线连起来。
4
6
3
7
2
5
6
8
3
9
9
21
3
4
1
3
2
3
10
25
【选自课本P65 做一做 第2题】
四、分数的意义和性质
右面两个圆的大小相同,蓝色部分和红色部分哪个大?为什么?
=
【选自课本P66 练习十六 第1题】
四、分数的意义和性质
下列分数中哪些没有化成最简分数?请把它们化成最简分数。
16
24
=
4
6
15
36
=
5
12
28
42
=
14
21
15
45
=
3
9
78
87
=
26
29
=
2
3
=
2
3
=
1
3
【选自课本P66 练习十六 第3题】
四、分数的意义和性质
观察下列分数的分子和分母,哪些有公因数2?哪些有公因数5?哪些有公因数3?
4
8
9
12
15
20
30
45
40
60
84
96
有公因数2
4
8
40
60
84
96
有公因数5
15
20
30
45
40
60
有公因数3
9
12
30
45
84
96
【选自课本P66 练习十六 第2题】
四、分数的意义和性质
把上下两行相等的两个分数用线连起来。
四、分数的意义和性质
先约分,再比较各组分数的大小。
四、分数的意义和性质
化简一个分数时,用2约了两次,用5
约了一次,得 。求原来的分数。
四、分数的意义和性质
把下列分数填入相应的圈里。
【选自课本P66 练习十六 第5题】
四、分数的意义和性质
兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
35÷80=
7
16
喜欢的照片:
不喜欢的照片:
(80-35)÷80=
9
16
【选自课本P66 练习十六 第4题】
四、分数的意义和性质
先约分,再化成带分数。
15
12
20
12
77
21
70
32
90
80
150
60
【选自课本P67 练习十六 第9题】
四、分数的意义和性质
先约分,再化成带分数。
15
12
20
12
77
21
70
32
90
80
150
60
【选自课本P67 练习十六 第9题】
已知a=2×3×3×5,b=2×2×3×3×5,求a和b的公因数与最大公因数。
两个数共有的质因数或共有质因数的积,都是两个数的公因数。
a、b共有的质因数有2、3、3、5
2×3=6, 2×5=10,3×3=9,3×5=15,
2×3×3=18,2×3×5=30,3×3×5=45,
2×3×3×5=90
所以a、b的公因数有1、2、3、5、6、9、10、
15、18、30、45、90,最大公因数是90。
【选自课本P67 练习十六 第12题】
四、分数的意义和性质
下列分数中哪些在直线上能用同一个点表示?把它们在直线上表示出来。
1
0
3
12
6
24
7
14
4
16
3
6
【选自课本P66 练习十六 第6题】
四、分数的意义和性质
将48本练习本和64支铅笔平均分给若干名同学。如果练习本和铅笔都没有剩余,且保证分到练习本和铅笔的同学人数相同,最多能分给多少名同学
48和64的最大公因数是16。
最多能分给16名同学。
【选自课本P66 练习十六 第7题】
四、分数的意义和性质
小明的生活非常有规律,下面是他睡觉和起床的时间。
第一天晚上
第二天早上
小明睡觉的时间占全天的几分之几?
【选自课本P67 练习十六 第8题】
四、分数的意义和性质
10÷24 =
5
12
答: 他每天大约有 的时间处于睡眠状态。
5
12
第一天晚上
第二天早上
先约分,再比较各组分数的大小。
12
16
和
9
12
4
12
和
5
20
4
14
和
9
21
70
35
和
90
40
3
4
3
4
1
3
1
4
=
>
2
7
3
7
2
9
4
<
<
【选自课本P67 练习十六 第10题】
(1)以分米作单位,用分数分别表示长方形的长和宽。
4
5
分米
长:
3
5
分米
宽:
6cm
8cm
【选自课本P67 练习十六 第11题】
四、分数的意义和性质
4
3
长是宽的:8÷6=
3
4
宽是长的:6÷8=
(2)长方形的长是宽的几分之几?宽是长的几分之几?
6cm
8cm
【选自课本P67 练习十六 第11题】
可以用对角线将长方形平均分成两份,涂其中一份;也可以用对称轴将长方形平均分成两份,涂其中一份。
1
2
(3)涂出长方形面积的 ,你可以怎样涂?
6cm
8cm
【选自课本P67 练习十六 第11题】
*化简一个分数时,用2约了两次,用3约了一次,得 。求原来的分数。
3
8
3×2×2×3
8×2×2×3
=
36
96
36
96
答:原来的分数是 。
【选自课本P67 练习十六 第13题】
四、分数的意义和性质
填一填。
1.分母是8的真分数有( )个,其中最
简真分数有( )。
2.把 约分,可以用分子和分母的最大公
因数( )去约,结果是( )。
7
12
四、分数的意义和性质
3.在 和 中,与 相等的分数是( )。
4.一个最简真分数,分子与分母的和是20,这样
的分数有 ( )个。
5.一个最简真分数,分母与分子的积是24,这个
真分数可能是( )。
4
先约分,再化成带分数。
四、分数的意义和性质
路路家离学校有150 m,她从家里步行去学校,已经走了60 m。她已走的路程和剩下的路程分别占总路程的几分之几
四、分数的意义和性质
公倍数和最小公倍数:
两个数公有的倍数,叫作它们的公倍数。
其中最小的公倍数,叫作它们的最小公倍数。没有最大的公倍数。
我们也可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。
60 42
60=2×2×3×5
42=2×3×7
2
30
21
3
10
7
最小公倍数:
2×3×2×5×7
=420
最小公倍数:
2×3×10×7
=420
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公因数1为止
60 和 42
如果 a 是 b 的倍数,那么 a 是它们的最小公倍数。
如果 a 和 b 互质,那么它们的最小公倍数就是 ab。
找出下列每组数的最小公倍数。
8和10 6和15 6和9
4和15 1和7 4和10
40
30
18
60
7
20
【教材P71练习十七 第2题】
四、分数的意义和性质
下面每组数的公倍数中有没有36?有没有48?有没有84?
6和18 21和14 12和8 9和24
36
84
48
公倍数中没有36,48,84
【教材P71练习十七 第3题】
四、分数的意义和性质
按照从小到大的顺序,在100以内的数中找出6的倍数和10的倍数,再找出它们的公倍数和最小公倍数。
6的倍数:6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96。
10的倍数:10,20,30,40,50,60, 70,80,90。
6和10的公倍数是30,60,90;
最小公倍数
【教材P71练习十七 第1题】
求下列每组数的最小公倍数。
10 和 15
16 和 24
8 和 12
18 和 12
18 和 9
9 和 10
30
48
24
36
18
90
四、分数的意义和性质
选一选。 (将正确答案的序号填在括号里)
1.连续两个自然数( 0除外)的乘积一定是这两
个数的( ).
A.最大公因数 B.最小公倍数 C.公因数
B
四、分数的意义和性质
2.两个数的公倍数一定是这两个数( )。
A.倍数 B.因数 C.公倍数
A
3. a,b是不为 0 的自然数,已知 a ÷ b = 5,
那么 a 和 b 的最小公倍数是( )。
A.5 B.a C.b
B
4. 100 是 25 和 50 的 ( ).
A.最小公倍数 B. 最大公因数 C.公倍数
C
写出每组分数的两个分母的最小公倍数。
72
100
60
240
四、分数的意义和性质
判断下面的说法是否正确,并说一说你的理由。
(1)两个数的最小公倍数一定比这两个数都大。
(2)两个数的积一定是这两个数的公倍数。
√
×
【教材P71 练习十七 第4题】
四、分数的意义和性质
每只蝴蝶只落在自己数字的倍数的花朵上。哪朵花上两只蝴蝶都会停留?
24、48、72这3朵花上蝴蝶都会停留。
【教材P71 练习十七 第5题】
四、分数的意义和性质
在括号里写出每组分数的两个分母的最小公倍数。
和
和
和
【教材P71 练习十七 第7题】
( )
( )
( )
12
24
18
四、分数的意义和性质
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形 (用的地砖必须都是整块的), 正方形的边长可以是多少分米 最小是多少分米
四、分数的意义和性质
参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
四、分数的意义和性质
李阿姨家的月季每4天浇一次水,君子兰每6天浇一次水。李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日
【教材P71 练习十七 第6题】
四、分数的意义和性质
4和6的最小公倍数是12;
1+12=13(日)
答:下一次再给这两种花同时浇水应该是5月13日。
爸爸、妈妈带着小红和弟弟一起跑步。爸爸每跑一圈用时3分钟,妈妈每跑一圈用时4分钟,小红每跑一圈用时6分钟。
【教材P72 练习十七 第10题】
四、分数的意义和性质
(1)如果爸爸、妈妈在起点同时起跑,至少多少分钟后两人在起点再次相遇 此时爸爸、妈妈分别跑了多少圈
下面各组数有没有公因数2?有没有公因数3?有没有公因数5?
6和9 10和18 15和30 20和8
3
2
3、5
2
【教材P72 练习十七 第8题】
四、分数的意义和性质
3 路: 每 6 分钟发一次车
5 路: 每 8 分钟发一次车
3路和5路公共汽车的起点站相同。这两路公共汽车同时发车后,过多少分钟两路车第二次同时发车
24分钟
【教材P72 练习十七 第9题】
四、分数的意义和性质
* 36可能是哪两个数的最小公倍数?你能找出几组?
如36和1,36和2,36和3,36和4,36和6,36和9,36和12,36和 18;
4和9,4和18,9和12,12和18。共12组。
【教材P72 练习十七 第11题】
四、分数的意义和性质
五(1)班分组进行拔河比赛,不管是8人一组,还是10人一组,都刚好分完。五(1)班有多少人
8和10的公倍数有40,80,… 40<50,五(1)班有40人。
四、分数的意义和性质
体育馆站是6路和18路公共汽车的起点站,6路公共汽车每5分钟发一次车,18路公共汽车每6分钟发一次车。这两路公共汽车在6:00同时发车后,下一次同时发车是什么时候
5和6的最小公倍数是30,故下一次同时发车是6:30。
四、分数的意义和性质
,
,
①
②
分母相同
分子相同
比较分子,分子大的
分数就大。
比较分母,分母大的
分数就小。
四、分数的意义和性质
在 里填上“>”“<”或“=”。
5
7
3
7
7
16
11
16
3
5
3
4
4
9
4
5
<
<
<
<
11
21
13
21
19
25
9
25
10
19
10
13
15
17
15
22
<
>
<
<
四、分数的意义和性质
像这样,把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
异分母分数
同分母分数
分数的基本性质
与原分数相等
四、分数的意义和性质
在 中填上“>”“<”或“=”。
3
13
7
13
5
6
5
8
2
3
3
5
4
30
2
15
>
>
>
=
说一说:怎样比较分数的大小?
【教材P74 做一做 第1题】
四、分数的意义和性质
把下面每组中的两个分数通分。
2
3
和
1
5
3
4
和
5
8
2
3
=
10
15
1
5
=
3
15
3
4
=
6
8
5
6
和
8
15
4
7
和
6
11
5
6
=
25
30
8
15
=
16
30
4
7
=
44
77
6
11
=
42
77
【教材P74 做一做 第2题】
把下面每组中的两个分数通分。
5
6
和
7
8
3
7
和
2
9
5
6
=
20
24
7
8
=
21
24
3
7
=
27
63
4
9
和
7
18
3
8
和
5
9
2
9
=
14
63
4
9
=
8
18
3
8
=
27
72
5
9
=
40
72
【教材P74 做一做 第2题】
比较每组中两个分数的大小,再和同学交流一下你的方法。
8
9
5
6
1
3
3
7
2
5
3
10
5
8
7
10
<
<
>
<
【教材P75 练习十八 第2题】
四、分数的意义和性质
1.把异分母分数( )化成和( )相等的( )分数,叫作通分。
2.通分时选用的公分母一般是原来几个分母的( )。
3.通分的方法先求出原来几个分母的( )
然后把各分数分别化成用这个( )作分母的分数。
分别
最小公倍数
最小公倍数
最小公倍数
原来分数
同分母
四、分数的意义和性质
4.通分的依据( )。
分数的基本性质
5.通分的目的是把( )分母的分数化成( )分母的分数。
异
同
比较每组中两个分数的大小。
3
8
1
8
11
25
17
25
5
7
5
17
12
23
12
19
<
<
>
<
【教材P75 练习十八 第1题】
四、分数的意义和性质
=
4×( )
5×( )
=
( )
( )
4
5
把下面每组中的两个分数通分。
=
6×( )
7×( )
=
( )
( )
6
7
(1)
【教材P75 练习十八 第5题】
四、分数的意义和性质
=
9× ( )
10×( )
=
( )
( )
9
10
=
3×( )
4×( )
=
( )
( )
3
4
(2)
在 里填上“>”“<”或“=”。
2
3
5
6
5
12
5
11
19
20
14
15
13
16
3
2
>
>
>
>
【教材P76 练习十八 第8题】
四、分数的意义和性质
亚洲陆地面积约占全球陆地面积的,非洲和南美洲的陆地面积分别约占全球陆地面积的和。亚洲、非洲和南美洲这三个洲中,哪个洲的陆地面积最大 哪个最小
【教材P75 练习十八 第6题】
四、分数的意义和性质
3
10
3×5
10×5
=
=
15
50
1
5
1×10
5×10
=
=
10
50
3
25
3×2
25×2
=
=
6
50
15
50
,
,
,因为
>
10
50
>
6
50
,
所以
3
10
>
1
5
>
3
25
。亚洲的陆地面积最大,
南美洲的陆地面积最小。
把下面分数按从小到大的顺序排列起来。
4
5
11
12
5
6
4
3
7
10
1
2
1
2
<
7
10
<
4
5
<
5
6
<
11
12
<
4
3
【教材P76 练习十八 第9题】
四、分数的意义和性质
把下列分数填入相应的圈里。
大于
小于
【教材P75 练习十八 第3题】
四、分数的意义和性质
张叔叔和李叔叔参加工厂的技能比赛。张叔叔加工完所有零件的时,李叔叔加工完所有零件的。在这段时间里,谁的比赛成绩更好一些?
因为 = , = , < ,所以 < ,
在这段时间里,李叔叔的比赛成绩更好一些。
1
2
5
10
3
5
6
10
5
10
6
10
1
2
3
5
【教材P75 练习十八 第4题】
四、分数的意义和性质
五(1)班要为图书角选购一批新书,班长决定先作一个意向调查。下面是调查结果(每人只选一种)。
应该怎样选购图书?说一说你的理由。
课外读物种类
喜欢的人数占全班总人数的几分之几
科普类
童话类
历史类
7
12
1
6
1
4
【教材P76 练习十八 第7题】
四、分数的意义和性质
1
6
=
2
12
1
4
=
3
12
7
12
>
1
4
,
,
>
1
6
。
所以,应该多选购科普类图书,少选购童话类图书。
最大公因数
最大公因数和最小公倍数的积
两个数的积
最小公倍数
10和20
8和12
9和21
7和11
4.按要求填写下表,看看你有什么发现。
10
4
3
1
20
24
63
77
200
96
189
77
200
96
189
77
你能再举例验证自己的发现吗?
【教材P76 练习十八 第10题】
四、分数的意义和性质
你能写出一个比 大又比 小的分数吗?你是怎样找到这个分数的?你还能再找到两个这样的分数吗?
1
5
1
6
11
60
、
16
90
、
17
90
……(答案不唯一)
、
【教材P76 练习十八 第11题】
四、分数的意义和性质
填空。
(1)0.6表示 。0.09表示 。
(2)0.5表示 。
(3)0.006里面有( )个千分之一,它表示
( )分之( ),写成分数是 。
6
10
9
100
5
10
6
千
六
6
1000
四、分数的意义和性质
把0.7 、 、0.25 、 、 、
10
9
100
43
25
7
47
13
按从小到大的顺序排列起来。
10
9
﹦0.9
100
43
﹦0.43
25
7
﹦7÷25﹦0.28
﹦13÷47≈0.277
47
13
0.25
<
47
13
<
25
7
100
43
<
<
0.7
<
10
9
四、分数的意义和性质
填空
把0.25化成分数时,因为0.25是( )小数,所以就在1后面写( )个0作( ),把0.25去掉小数点作( ),最后是( )。
两位
2
分母
分子
四、分数的意义和性质
0.3
3
10
0.25
1
4
0.4
2
5
分别用小数和分数表示下面各图中涂色部分的大小。
【选自课本P77 练习十九 第1题】
四、分数的意义和性质
把相等的小数和分数用线连起来。
【选自课本P77 练习十九 第3题】
四、分数的意义和性质
把下面的小数化成分数,分数化成小数(除不尽的保留两位小数)。
0.2
0.4
0.56
0.76
0.375
1.625
四、分数的意义和性质
0.5625
0.35
0.049
1.2
0.22
0.17
1.(1) 0.8里面有8个( )分之一,表示( )分之( ),化成分数是 。
(2) 0.05里面有5个( )分之一,化成分数是 。
(3) 0.007里面有7个( )分之一,化成分数是 。
(4) 0.36里面有36个( )分之一,化成分数是 。
十
十
八
4
5
百
1
20
千
7
1000
百
9
25
【选自课本P78 练习十九 第2题】
四、分数的意义和性质
把下列各数按从大到小的顺序排列起来。
【选自课本P79 练习十九 第8题】
四、分数的意义和性质
猎豹的速度是小汽车速度的多少倍 小汽车的速度是猎豹速度的几分之几
【选自课本P78 练习十九 第4题】
答:猎豹的速度是小汽车速度的1.55倍,
小汽车的速度是猎豹速度的 。
四、分数的意义和性质
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些
【选自课本P79 练习十九 第10题】
四、分数的意义和性质
0.31
0.08
0.23
0.44
0.83
0.22
1.15
把下面的分数化成小数(除不尽的保留两位小数)。
【选自课本P78 练习十九 第5题】
四、分数的意义和性质
在 里填上适当的小数,在 里填上适当的分数。
【选自课本P79 练习十九 第6题】
四、分数的意义和性质
用小数表示 用分数表示
40cm ( )m ( )m
150g ( )kg ( )kg
125cm2 ( )dm2 ( )dm2
3680dm3 ( )m3 ( )m3
在括号里填上适当的数。
【选自课本P79 练习十九 第7题】
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
【选自课本P79 练习十九 第9题】
四、分数的意义和性质
下面的分数与小数的互化是否正确?
四、分数的意义和性质
下面这些分数中哪些可以化成有限小数?
√
√
√
√
√
判断前看分数是不是最简分数
把最简分数的分母分解质因数:
8=2×2×2
40=2×2×2×5
21=3×7
30=2×3×5
四、分数的意义和性质
1.
( )>( )>( )>( )
2.
( )<( )<( )<( )
四、分数的意义和性质
解决问题。
一块正方形布料,既可以裁成若干条边长是8cm的方巾,也可以裁成若干条边长是10 cm的方巾,且都没有剩余。这块正方形布料的边长至少是多少厘米
四、分数的意义和性质
因为8和10的最小公倍数是40。
答:这块正方形布料的边长至少是40厘米。
8 cm
10 cm
把一根2m长的木条锯成同样长的4段,每段是这根木条的 ,每段长
( )÷ ( )= ( )m = m。
【选自课本P81 练习二十 第1题】
4
0.5
2
1
4
1
2
( )
( )
( )
( )
四、分数的意义和性质
【选自课本P82 练习二十 第2题】
判断下面的说法是否正确,并说一说你的理由。
(1)分数的分母越大,它的分数单位就越小。( )
(2)分数都比整数小。 ( )
(3)假分数的分子都比分母小。 ( )
×
√
×
假分数比整数大或相等
假分数的分子可能大于或等于分母
四、分数的意义和性质
(5)分子和分母的公因数只有1的分数是最简分数。
( )
(4)如果 b 是 a 的2倍(a,b为非零自然数),那么 a、b 的最大公因数是a ,最小公倍数是b 。 ( )
√
√
在横线上填写适当的分数。
【选自课本P82 练习二十 第4题】
25cm= ______m 36dm2 = ______m2
600g= ______kg 750mL = ______L
0.28dm= ______dm 258cm3 = ______ dm3
四、分数的意义和性质
在 里填上“>”“<”或“=”。
5
13
8
13
5
7
5
11
4
5
7
8
2
9
1
6
<
<
<
<
【选自课本P82 练习二十 第6题】
四、分数的意义和性质
你听过“冰山一角”的说法吗 冰山露在水面上的只是它的一小部分,大部分隐藏在水面下。假设一座冰山的体积是1000m3,它露在水面上的体积是100m3。冰山露在水面上的体积占总体积的 ,水面下的体积占总体积的 。
10
1
10
9
【选自课本P81 练习二十 第3题】
四、分数的意义和性质
一座喷泉由内外两层构成。外层每10分钟喷水一次,内层每6分钟喷水一次。12:45同时喷过一次水后,下次同时喷水是几时几分
6和10的最小公倍数是30。
12:45过30分是13:15
答:下次同时喷水的时间是13:15。
四、分数的意义和性质
可以怎样填?
第一题可以填: 、 、 、…
第二题可以填: 、 、 、…
【选自课本P82 练习二十 第11题】
四、分数的意义和性质
48和54的最大公因数是6。
答:每组最多有6人。
五、六年级学生参加学校大扫除,五年级来了48人,六年级来了54人。如果把两个年级的学生分别分成若干小组,要使两个年级每个小组的人数相同,每组最多多少人
【选自课本P81 练习二十 第5题】
四、分数的意义和性质
某学校五年级学生一共有150人,体质健康测试优良的为60人。其中五(1)班有38人,体质健康测试优良的为19人。五(1)班同学体质健康测试优良情况和五年级的总体情况相比怎么样
60 ÷ 150 = 19 ÷ 38 =
因为 , = ,所以 。
答:五(1)班班同学体质健康测试优良情况和五年级的总体情况相比稍好一些。
【选自课本P82 练习二十 第7题】
四、分数的意义和性质
(1) 3÷5 =
文文的纸飞机飞了5m,小刚的飞了4m,兰兰的飞了3m。
(1)兰兰的纸飞机飞的距离是文文的几分之几?
(2)你还能提出其他数学问题并解答吗?
四、分数的意义和性质
(2)答案不唯一
小刚的纸飞机飞的距离是文文的几分之几?
文文的纸飞机飞了5m,小刚的飞了4m,兰兰的飞了3m。
(1)兰兰的纸飞机飞的距离是文文的几分之几?
(2)你还能提出其他数学问题并解答吗?
【选自课本P82 练习二十 第9题】
果农准备将一批石榴进行分装。如果每8个装一盒,会剩下3个;如果每9个装一盒,也会剩下3个。这批石榴至少有多少个
8和9的最小公倍数是72
72+3=75(个)
答:这批石榴至少有75个。
四、分数的意义和性质
1. 4 的分数单位是( ),它有( )个
这样的分数单位。
2. 把5个苹果平均分给8个小朋友,每人分得这
些苹果的 ,每人分得( )个。
填一填。
( )
( )
32
8
1
四、分数的意义和性质
3.分母是10的最简真分数的和是( )。
4.在横线上填写适当的分数。
26cm=_____m
35dm2=_____m2
400g=_____kg
150mL=_____L
850cm3=_____dm3
15分=_____时
2
知识点归纳总结:
1.点----线----面----体;
2.根据一个方向观察到的形状摆小正方体,有多种摆法,无法确定立体图形形状;
3.根据三个方向观察到的形状摆小正方体,只有一种摆法。
4.从正面、左面、上面三个不同的方向观察同一组物体而画出的图形就是三视图。
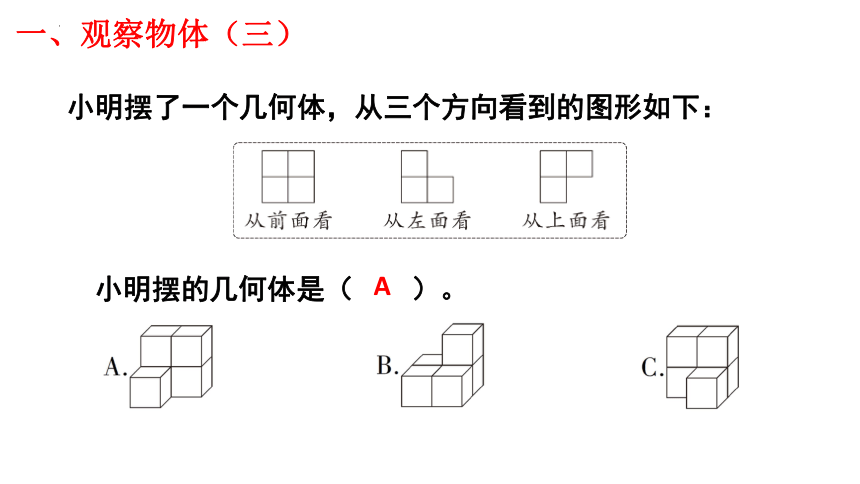
一、观察物体(三)
小明摆了一个几何体,从三个方向看到的图形如下:
小明摆的几何体是( )。
A
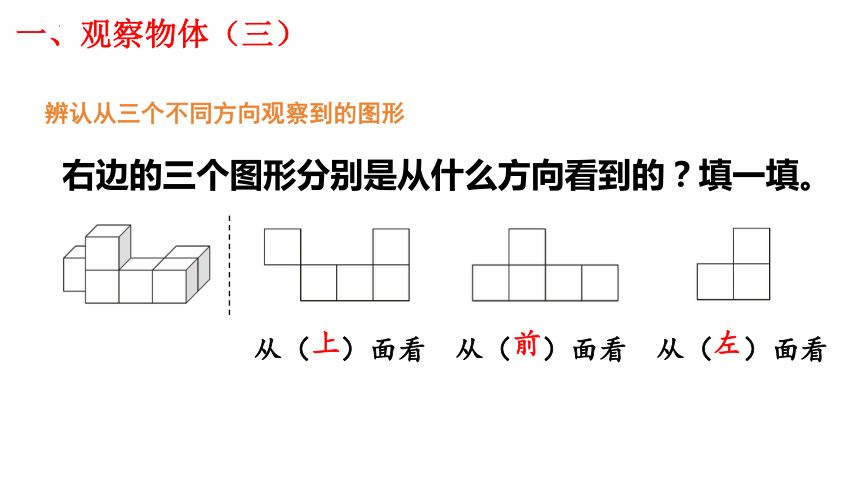
一、观察物体(三)
右边的三个图形分别是从什么方向看到的?填一填。
从( )面看
从( )面看
从( )面看
上
前
左
辨认从三个不同方向观察到的图形
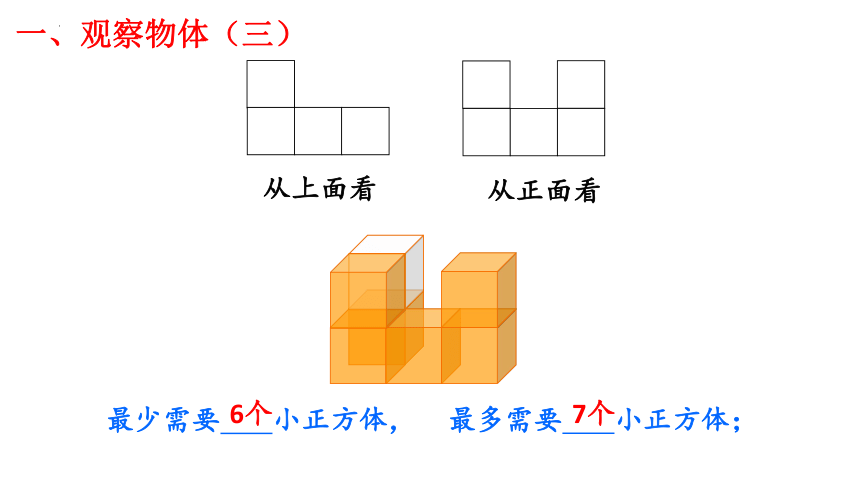
一、观察物体(三)
从上面看
从正面看
最少需要 小正方体,
最多需要 小正方体;
6个
7个
一、观察物体(三)
倍数与因数的概念:
二、因数与倍数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
注意:
1.因数与倍数是相互依存的,不能单独存在;
2.一个数的因数的个数是有限的,倍数的个数是无限的;
3.一个数的最大因数=最小倍数=它本身;
4.一个数因数的求法:成对的按顺序找;
5.一个数倍数的求法:依次乘以自然数。
奇数与偶数的运算规律:
奇数±奇数=偶数
奇数±偶数=奇数
偶数±偶数=偶数
奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
2、3、5的倍数特征:
◆ 2的倍数特征:个位上是0、2、4、6、8的数都是2的倍数;
◆ 3的倍数特征:一个数各位上的数的和是三的倍数,这个数
叫3的倍数;
◆ 5的倍数特征:个位上是0、5的数都是5的倍数。
奇数、偶数、质数和合数:
◆奇数:
◆偶数:
◆质数:
◆合数:
不能被2整除的数叫奇数(个位上是1,3,5,7,9的数);
能被2整除的数叫偶数(个位上是0,2,4,6,8的数);
只有1和它本身两个因数的数叫做质数;
除了1和它本身还有其他因数的数叫做合数。
◆1只有一个因数,所以1既不是质数,也不是合数。
特殊的数:
最小的偶数是( ),最小的奇数是( ),最小的质数是( ),最小的合数是( ),( )既不是质数,也不是合数。
0
1
2
4
1
在自然数中,有一个数很特殊,大家知道是哪一个数吗?
0÷3=0
0×3=0
0×10=0
0÷10=0
例如:
0有很多特殊性,如0乘一个数还得0,0不能作除数等。
注意:为了方便,在研究因数和倍数的时候,我们所指的
数是自然数(一般不包括0)。
下面说法对吗?
(2)1.8÷0.3=6,0.3是1.8的因数,1.8是0.3的倍数。
(1)6÷5=1.2, 5是6的因数,6是5的倍数。
(4)54÷6=9,6是因数,54是倍数 。
(3)24÷3=8, 8是24的因数,24是8的倍数 。
( )
( )
( )
( )
×
×
√
×
(说说你的理由)
辨一辨。 (对的画“√”,错的画“ ”)
1. 6 ÷ 6 =1,这里 6 既是因数,也是倍数。
( )
2. 28是7的倍数。
( )
24 和 16 都是 8 的倍数, 8 既是 24 的因数,也
是16的因数。
( )
4. 自然数 1,2,3,…都是 1 的倍数。
( )
5. 3.6 是 9 的倍数。
( )
√
√
√
×
仔细观察找到的因数,你们发现了什么?
18的因数有 1 ,2 ,3 ,6 ,9 ,18 。
30的因数有 1 ,2 ,3 ,5 ,6 ,10 ,15 ,30 。
36的因数有 1 ,2 ,3 ,4 ,6 ,9 ,12 ,18 ,36 。
1
1
1
一个数的最小因数是_____,最大因数是________。
一个数的因数的个数是________。
1
它本身
有限的
仔细观察,你发现这些数的倍数有哪些特征呢?
2的倍数有 2 ,4 ,6 ,8 ,10 ,12,···
3的倍数有 3,6,9,12,15,18,···
5的倍数有 5,10,15,20,25,30,···
一个数的最小倍数是_______,_____最大倍数。
一个数的倍数的个数是________。
它本身
无限的
没有
判断下面的说法是否正确,并说一说你的理由。
(1)1是1,2,3,…的因数。 ( )
(2)8的倍数只有16,24,32,40,48 ( )
(3)36÷9=4,所以36是9的倍数。 ( )
(4)5.7是3的倍数。 ( )
√
×
×
√
【选自教材P7 练习二 第5题】
1、在26、12和13这三个数中,( )是( )的倍数,( )是( )的因数。
2、一个数,千位上是最小的质数,百位上是最小的奇数,个位是最小的合数,其余数位上的数字是0,这个数写作( )。
3、一个数的最大因数是36 ,这个数是( ),这个数的最小倍数是( )。
4、一个两位数同时是2、5、3的倍数,这个两位数最大是( ),最小是( )。
26
13
13
26
2104
36
36
90
30
从0、4、5、8、9中选取三个数字组成三位数:
(1)在能被2整除的数中,最大的是( ),最小的是( );
(2)在能被3整除的数中,最大的是( ),最小的是( );
(3)在能被5整除的数中,最大的是( ),最小的是( )。
984
408
984
405
985
405
2.菲菲家的电话号码是一个八位数,记为:ABCDEFGH。已知:A是最小的质数,B是最小的合数,C既不是质数也不是合数,D是比最小的质数小2的数,E是10以内最大的合数,F只有因数1和5,G是8的最大因数,H是6的最小倍数。
答:菲菲家的电话号码是:24109586。
猜数游戏。
【选自教材P8 练习二 第7题】
它是42的因数,
又是7的倍数。
它可能是7,14,
21,42中的一个。
我知道了,它是_______。
42
它也是2和3的
倍数。
一个数比20小,它既是2的倍数,又有因数7,这个数
是( )。
一个数的最大因数和最小倍数都是9,这个数是( )。
14
9
填空。
(1)1 的因数有 个,7 的因数有 个,10 的因数有 个。
(2)一个数的最大因数和最小倍数都是18,这个数是 。
(3)一个数的最小倍数是1,这个数是 。
1
2
4
【选自教材P8 练习二 第6题】
18
1
按要求填写数字。
【选自教材P11 练习三 第2题】
(1) 两个数位上的数相同,并且是5的倍数。
(2)3 5 既是2的倍数, 又是5的倍数。
(3) 既是2的倍数, 又是5的倍数的最小三位数。
5
5
0
1
0
0
下面的说法对吗?说出理由。
(1)一个自然数不是奇数就是偶数。 ( )
(2)偶数都比奇数大。 ( )
(3)个位上是2,4,6,8,0的自然数都是偶数。 ( )
(4)一个数是2的倍数,那么它一定是偶数。 ( )
(5)能被2,5整除的数个位上的数字一定是0。 ( )
√
×
√
√
√
【选自教材P11 练习三 第5题】
在□里填一个数字,使组成的每个数都是3的倍数。各有几种填法?
□7 4□2 □44 65□ 12□1
2
5
8
0
3
6
9
1
4
7
1
4
7
2
5
8
辩一辩。(对的画“√”,错的画“×”)
1.因为33,36,39,63,69,156这些数都是3的倍数,所以个位
上是3,6,9的数一定是3的倍数。
2.用4,5,6这三个数字,无论怎样排列成没有重复数字
的三位数,一定是3的倍数。
3.3的倍数一定是奇数。
4.一个数是6的倍数,就一定是2,3的倍数。
( )
( )
( )
( )
×
√
×
√
(1)既是2和5的倍数,又是3的倍数的最小两位
数是 。
(2)既是2的倍数,又是3的倍数的最小三位数
是 ,最大三位数是 。
30
102
996
【见教材P13 练习三 第12题】
个位是0
(十位+个位)是3的最小倍数
个位是0,2,4,6,8
百位+十位+个位=3
“一五,一十,十五,二十……”这样数数,数出来的数都是_____的倍数,第12个数是______。
5
60
100,98,96,94,…,8,6,4,2。这些数中的每个数都是____的倍数,其中第15个数是____。
2
72
(1)
(2)
五、自主练习
【见教材P11 练习三 第6题】
在 里填一个数字,使组成的每个数既是2和3的倍数,
又是5的倍数。
6
15
3 0
40
5 0
60
0
0
0
3
6
9
2
5
8
1
4
7
3
6
9
填一填。
1.在12,14,16,32,124,640,6中,是4的倍数的有
( )。
2.既是3的倍数,又是5的倍数的最小三位数是( ),
同时是2,3,5的倍数的最小三位数是( ),
最大三位数是( )。
12,16,32,124,640
105
120
990
一个四位数417 。
(1)要使它是偶数, 里可以填( )。
(2)要使它是3的倍数, 里可以填( )。
(3)要使它既有因数2,又有因数5, 里可以填( )。
0,2,4,6,8
0,3,6,9
0
1有几个因数?
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
质数
合数
1
2,3,5,7,11,13,17,19
4,6,8,9,10,12,
14,15,16,18,20
1(既不是质数
也不是合数)
非零自然数按照因数的个数可以分为几类?
非0自然数
判断下面的说法是否正确,并说一说你的理由。
(1)所有的奇数都是质数。
【选自教材P16 练习四 第1题】
(2)所有的偶数都是合数。
(3)在1,2,3,4,5,…中,除了质数以外都是合数。
(4)两个质数的和是偶数。
不正确,如9是奇数又是合数。
不正确,如2是偶数又是质数。
不正确,1既不是质数又不是合数。
不正确,举例:质数2和3,2+3=5,5是奇数。
我们两个的和是10。
我们两个的积是21。
我们两个的和是20。
我们两个的积是91。
我是最小的质数。
我是最小的合数。
3和7
13和7
2和4
你知道下面的数各是多少吗?
【选自教材P16 练习四 第3题】
1.所有的质数都是奇数,所有的合数都是偶数。
2.自然数可分为奇数和偶数,也可以分为质数和合数。
3. 91是奇数,也是合数。
4.除0和2以外,所有的偶数都是合数。
5.质数加质数的和一定是合数。
辨一辨。(对的画“√”, 错的画“×”)
( )
( )
( )
( )
( )
×
×
√
×
√
选一选。(将正确答案的序号填在括号里)
1.一个合数至少有( )个因数。
A.2 B. 3 C.4
2.10以内既是奇数又是合数的数有( )个。
A.0 B.1 C.2
B
B
质数与质数的积( )。
A.一定是合数
B.一定是质数
C.可能是质数,也可能是合数
A
两个自然数相加,和的奇偶性我们可以确定,如果是多个自然数相加呢?
(1)偶数+偶数+偶数+······+偶数
(2)奇数+奇数+奇数+······+奇数
=
偶数
①奇数个奇数相加,和是奇数;
②偶数个奇数相加,和是偶数。
1+2+3+4+……+98+99 ,如果不计算,你能很快说出这道算式的和是奇数还是偶数吗?
偶数个奇数的和是偶数,其它偶数的和也是偶数,
所以1+2+3+4+······+98+99的和是偶数。
1+2+3+4+……+98+99
50个奇数
不计算,直接判断结果是奇数还是偶数。
46 + 27( ) 34 + 108 ( )
13×72 ( ) 268 × 54 ( )
89 +415 ( ) 71 × 67 ( )
奇数
奇数
偶数
偶数
偶数
偶数
结合图形抽象出面、棱、顶点。
面
棱
(面和面相交的线段)
顶点
(棱和棱的交点)
三、长方体和正方体
①认识长方体的长、宽、高。
长
宽
高
相交于同一顶点的3条棱的长度分别叫作长方体的长、宽、高。
长方体的长、宽、高是相对的,
左右竖着的棱称为高,
左右横着的棱称为宽。
一般把前后横着的棱称为长,
三、长方体和正方体
长方体和正方体的特征:
形体 相同点 不同点 联系
面 棱 顶点 面的形状 面的面积 棱长
长方体
正方体
6
个
12
条
8
个
6个面都是长方形。(特殊情况有两个相对的面是正方形)
6个面都是正方形
相对的两个面的面积相等
6个面的面积都相等
相对的棱的长度相等
12条棱的长度都相等
正方体是一种特殊的长方体
三、长方体与正方体
表面积 体积 容积
意义
计算 方法
常用计量单位
单位间进率
长方体或正方体6个面的总面积
物体所占空间的大小
容器所能容纳物体体积的大小
S长=2ab+2ah+2bh
=(ab+ah+bh) ×2
S正=a2×6
V长= abh
V正= a3
V=sh
长方体、正方体的意义、表面积、体积及容积
m 、dm 、cm
m 、 dm 、cm
m 、 dm 、 cm
、L 、 ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
1L=1000ml
1dm =1L
1cm =1ml
同体积
(从里面量)
三、长方体和正方体
(三)如何计算不规则物体的体积?
判断哪组的小棒可以搭成长方体。
小棒长度 ① ② ③
15cm 5根 4根 8根
10cm 4根 4根 0根
8cm 3根 4根 4根
三、长方体和正方体
算出下图中长方体的棱长和。
(长+宽+高)×4
三、长方体和正方体
(10+4+6)×4
=20×4
=80(cm)
(3+7+3)×4
=13×4
=52(cm)
三、长方体和正方体
6个面,相对的两个面完全相同。
12条棱,相对的棱长度相等。
8个顶点。
长
宽
高
长方体的特征
三、长方体和正方体
一个长、宽、高分别为 40 cm、30 cm、20 cm 的
小纸箱,在所有的棱上粘上一圈胶带,至少需要
多长的胶带?
20×4+30×4+40×4=360(cm)
【选自教材P21 练习五 第2题】
或(20+30+40)×4=360(cm)
答:至少需要360cm 的胶带。
三、长方体和正方体
选一选。 (将正确答案的序号填在括号里)
长方体有( )个顶点,( )个面,( )个棱。
A.6 B.8 C.12
B
1.
A
C
长方体中有( )组相对的面的面积分别相等。
A.3 B.2 C.1
A
2.
三、长方体和正方体
用一根长 60 cm 的铁丝正好可以焊接一个长 6 cm,宽 5 cm,高( )cm 的长方体框架。
A.4 B.16 C.8
A
三、长方体和正方体
(1)正方体的6个面 。
(2)正方体的12条棱 。
完全相同
长度相等
三、长方体和正方体
正方体有12条棱,每条棱的长度相等,所以棱长和=棱长×12。
三、长方体和正方体
判断:长方体的6个面一定都是长方形。 ( )
长方体的6个面一般是长方形,但特殊情况下有两个相对的面是正方形。
×
三、长方体和正方体
一个正方体的棱长是3厘米,那么这个正方体的棱长总和是多少厘米?
3×12=36(厘米)
答:这个正方体的棱长总和是36厘米。
棱长总和=棱长×12
三、长方体和正方体
正方体
立方体
6个面完全相同。
8个顶点。
12条棱长度相等。
正方体的特征
正方体可以看成是长、宽、高都相等的长方体。
三、长方体和正方体
90×2+55×2+22×4=378(m)
答:工人叔叔至少需378m的彩灯线。
为迎接“五一”国际劳动节,工人叔叔要在礼堂的四周装上彩灯(地面的四边不装)。已知礼堂长90m,宽55m,高22m,工人叔叔至少需要多长的彩灯线?
【选自教材P21 练习五 第5题】
三、长方体和正方体
用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?
8×12÷4-(10+7)
=96÷4-17
=24-17
=7(厘米)
答:它的高应该是7厘米。
三、长方体和正方体
正方体的全部展开图
“一四一型”
“二三一型”
“三三型”
“二二二型”
( )
√
( )
√
( )
折叠后,下面哪些图形能围成左侧的正方体?在括号里画“√”。
【选自教材P23 做一做】
注意:任何正方体的展开图不能是“田字型”,也不能是“凹字型”。
三、长方体和正方体
长方体或正方体 6 个面的面积之和,叫作它的表面积。
用自己的话说一说什么叫做长方体或者正方体的表面积
三、长方体和正方体
长方体的表面积= 长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
a
b
c
S表= 2(ab+ah+bh)
三、长方体和正方体
正方体的表面积的计算方法是怎样的?
正方体的表面积= 棱长×棱长×6
a
S表=6a2
三、长方体和正方体
将下面的展开图围成正方体后,哪两个面分别相对?
春对______
秋对______
暮鼓对______
夏
冬
晨钟
【选自教材P25 练习六 第2题】
三、长方体和正方体
做一个长 5dm,宽 4dm,高 3dm的长方体布艺收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
= 47×2
= 94(dm2)
答:至少需要 94 平方分米的布。
【选自教材P25 练习六 第4题】
三、长方体和正方体
一个长0.75m、宽0.5m、高1.6m的简易衣柜需要换布罩
(如右图,没有底面)。至少需要用多少平方米布料?
【选自教材P24 做一做】
(0.75×1.6+0.5×1.6)×2+0.75×0.5
= 2×2+0.375
= 4.375(m2)
答:至少需要用4.375平方米布料。
三、长方体和正方体
长方体或正方体 6 个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S表= 2(ab+ah+bh)
正方体表面积=棱长×棱长×6
S表=6a2
长方体和正方体的表面积
三、长方体和正方体
计算下面长方体和正方体的表面积。
上、下每个面的面积是:___________________
前、后每个面的面积是:___________________
左、右每个面的面积是:___________________
长方体的表面积是:_________________或_____________
20×10=200(cm2)
20×8=160(cm2)
10×8=80(cm2)
200×2+ 160×2+ 80×2=880(cm2)
(200+ 160+ 80)×2=880(cm2)
三、长方体和正方体
每个面的面积是:___________________
正方体的表面积是:_________________
8×8=64(cm2)
64×6=384(cm2)
三、长方体和正方体
一个长方体礼品盒,长 20 cm,宽 12 cm,高 8 cm,如果包装这个礼品盒的用纸是其表面积的 1.2 倍,至少要用多少平方厘米的包装纸?
(20×12+20×8+12×8)×2 =992(cm2)
992×1.2 =1190.4(cm2)
答:至少要用1190.4平方厘米的包装纸。
三、长方体和正方体
下面哪些图形是正方体的展开图?
( )
( )
( )
( )
√
×
√
×
三、长方体和正方体
一个长方体的饼干盒,长 10 cm,宽 6 cm,高 12 cm。如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?
10 cm
6 cm
12 cm
分析:商标纸的面积是饼干盒前、后、左、
右四个面的面积之和。
【选自教材P25 练习六 第5题】
10×12 ×2+6 ×12 ×2 = 384(cm2)
答:这张商标纸的面积至少有
384平方厘米。
三、长方体和正方体
一个新建的游泳池长 50 m,长是宽的 2 倍,深 2.5 m。现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米的瓷砖?
50 m
25 m
2.5 m
分析:游泳池只有 5 个面。
【选自教材P26 练习六 第10题】
50÷2 = 25(m)
50×25+50×2.5×2+25×2.5×2 =1625( m2 )
答:一共需要贴 1625 平方米的瓷砖。
三、长方体和正方体
把一个棱长46cm的正方体纸箱各面都贴上红纸,作为捐款箱。
(1)至少需要多少平方厘米的红纸?
(开口处忽略不计)
(2)如果只在棱上粘贴一圈胶带纸,
一卷4.5m长的胶带纸够用吗?
【选自教材P25 练习六 第6题】
(1)46×46×6=12696(cm2)
(2)46×12=552(cm)=5.52m
5.52m>4.5m
答:(1)至少需要12696cm2的红纸。(2)不够用。
三、长方体和正方体
一个正方体玻璃鱼缸的棱长为3dm,制作这个鱼缸至少需要多少平方分米的玻璃?(上面没有盖。)
3×3×5=45(dm2)
答:至少需要玻璃45dm2。
【选自教材P26 练习六 第8题】
三、长方体和正方体
一个正方体礼品盒的棱长为1.2dm。如果包装这个礼品盒的用纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
1.2×1.2×6=8.64(dm2)
8.64×1.5=12.96(dm2)
答:至少要用12.96dm2的包装纸。
【选自教材P26 练习六 第9题】
三、长方体和正方体
学校要粉刷教室。已知教室的长是8m,宽是6m,高是3m,门窗的面积是11.4m2。如果每平方米需要花6元涂料费,粉刷这个教室需要多少涂料费?
8×6+8×3×2+6×3×2-11.4=120.6(m2)
120.6×6=723.6(元)
答:粉刷这个教室要花费723.6元。
【选自教材P26 练习六 第11题】
三、长方体和正方体
如何把右面这个长方体木块分成两个棱长为4cm的正方体?这两个正方体的表面积之和与原长方体的表面积相等吗?
表面积不相等。
【选自教材P26 练习六 第13题】
三、长方体和正方体
橡皮的体积约是 10____
电饭锅的体积约是 25____
集装箱的体积约是 40____
m3
dm3
cm3
【选自教材P32 练习七 第3题】
在横线上填写合适的体积单位。
三、长方体和正方体
下面是用棱长 1 cm 的小正方体拼成的几何体,它们的体积各是多少?
9cm3
8cm3
6cm3
4cm3
【选自教材P28 做一做 第2题】
三、长方体和正方体
填一填。
物体所占( )的大小叫做物体的体积,计量体积常用的单位有( )、( )和
( ),用字母表示是( )、( )和( )。
空间
立方厘米
立方分米
立方米
cm3
dm3
m3
三、长方体和正方体
棱长是( )的正方体的体积是 1 cm3;
棱长是( )的正方体的体积是 1 dm3 ;
棱长是( )的正方体的体积是 1 m3 。
1 cm
1 dm
1 m
厘米是用来计量( )的单位。
平方厘米是用来计量( )的单位。
立方厘米 是用来计量( )的单位。
长度
面积
体积
三、长方体和正方体
在括号里填出合适的体积单位。
一个抽纸盒的体积约为 2( )
一个牙膏盒的体积约为 480( )
dm3
cm3
三、长方体和正方体
一节火车车厢的体积约为 250( )
一本故事书的体积约为 300( )
m3
cm3
三、长方体和正方体
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=abh
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
三、长方体和正方体
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫作底面积。
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
三、长方体和正方体
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=abh
=15×7×5
=525(cm3)
答:它的体积是525cm3。
【选自教材P31 做一做 第1题】
三、长方体和正方体
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
长方体体积=底面积×高
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
三、长方体和正方体
把下表中长方体或正方体的相关数据补充完整。
512 m3
15 cm
52 dm2
三、长方体和正方体
算一算。
43=______
4×3=______
4+4+4=______
82=______
8×2=______
8+8=______
64
12
12
64
16
16
【选自教材P32 练习七 第6题】
三、长方体和正方体
【选自教材P33 练习七 第7题】
16×5×10=800(m3)
9×9×9=729(dm3)
3×3×10=90(cm3)
三、长方体和正方体
50cm=0.5m
50×30×0.5=750(m3)=750(方)
要在平地挖一个长 50 m、宽 30 m、深50 cm 的长方体土坑,一共要挖出多少方的土?
在工程上,土、沙、石等的体积常用“方”作单位,1方=1立方米。
【选自教材P33 练习七 第8题】
三、长方体和正方体
30×30×30=27000(cm3)
一块棱长 30 cm 的正方体冰块,它的体积是多少立方厘米?
【选自教材P33 练习七 第9题】
三、长方体和正方体
【选自教材P33 练习七 第10题】
14cm
200dm3
81m2
378cm3
三、长方体和正方体
2.4dm2=0.024m2
0.024×3×500=36(m3)=36(立方米)
答:这些方木一共是36平方米。
【选自教材P33 练习七 第11题】
三、长方体和正方体
单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
下面是我们学过的计量单位,请把下表补充完整。
3.5 dm3=_____cm3
700 dm3=_____m3
3500
0.7
0.25 m3=_______cm3
250000
×1000
÷1000
×1000
×1000
三、长方体和正方体
要砌一面长 15 m、厚 24 cm、高 3 m 的砖墙,如果每立方米用砖 525 块,至少要用砖多少块?
24 cm=0.24 m
V =abh
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:至少要用砖5670块。
【选自教材P35 做一做 第2题】
三、长方体和正方体
1.02 m3=______dm3
960 dm3=______m3
6270 cm2=_____dm2
36000 cm3=_____m3
8.63 m2=______dm2
23 dm3=_______cm3
1020
0.96
62.7
0.036
863
23000
【选自教材P36 练习八 第1题】
三、长方体和正方体
一个无盖的鱼缸,长 1.2 m,宽 80 cm,高 6 dm,这个鱼缸可以放多少立方分米的水?
1.2 m=12 dm 80 cm=8 dm
V = abh
=12×8×6
=576(dm3)
答:这个鱼缸可以放 576 dm3 的水。
三、长方体和正方体
辨一辨。 (对的画“√”,错的画“ ”)
1.体积单位间的进率是 1000。
2.1000个1 cm3的小正方体拼成的几何体的
体积是1 dm3。
( )
( )
√
三、长方体和正方体
3.棱长是 1 m 的大正方体可以切成 1000 个
棱长是 1 cm 的小正方体。
4.棱长为 6 cm 的正方体,它的表面积和
体积相等。
( )
( )
三、长方体和正方体
要在一块长25 m、宽9m的长方形地面上铺一层6 cm厚的沙土。一辆车每次能运送1.5 m3的沙土,所需的沙土至少需要用这辆车运送多少次
25×9×0.06 = 13.5(m3)
6 cm=0.06 m
13.5÷1.5 = 9(次)
答:至少需要用这辆车运送9次。
三、长方体和正方体
一个长方体包装盒,从里面量长 28 cm,宽 20 cm,里面的体积为 11.76 dm3。用它装一件长 25 cm、宽 16 cm、高 18 cm 的玻璃器皿,是否装得进去?说一说你的理由。
11.76 dm =11760 cm
11760÷(28×20)=21(cm)
21>18,可以装下。
【选自教材P36 练习八 第2题】
三、长方体和正方体
(100×45×4.5+45×5×35×2)×50
=1800000(cm3)
=1.8(m3)=1.8(方)
答:做这些凳子至少用了1.8方混凝土。
某小区新安装了50个混凝土凳子(如右图所示)。凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了多少方混凝土?
【选自教材P36 练习八 第3题】
三、长方体和正方体
“六一”儿童节前,小学生用棱长 3 cm的正方体塑料拼插积木在广场中央搭起了一面长 6 m、高 2.7 m、厚 6 cm 的心愿墙。这面墙一共用了多少块积木?
6m=600cm 2.7m=270cm
600×270×6÷(3×3×3)
=36000(块)
答:这面墙一共用了36000块积木。
【选自教材P36 练习八 第4题】
三、长方体和正方体
一个长方体的无盖玻璃水族箱,长是 6 m,宽是 60 cm,高是 1.5 m。制作这个水族箱需要用多少平方米的玻璃?它的体积是多少?
【选自教材P36 练习八 第5题】
三、长方体和正方体
60 cm=0.6 m
需要玻璃:6×0.6+(6×1.5+0.6×1.5)×2
=23.4(m2)
体积:6×0.6×1.5=5.4(m3)
答:制作这个水族箱需要用23.4m2的玻璃,它的体积是5.4m3。
38 dm=3.8 m
7.6÷(5×3.8)=0.4(m)
将 7.6 m3 的沙子铺在一个长 5 m、宽 38 dm 的沙坑里,可以铺多厚?
答:可以铺0.4m厚。
【选自教材P37 练习八 第6题】
三、长方体和正方体
修建长城所用的某块砖的尺寸如右图所示。这块长城砖的体积是多少?
【选自教材P36 练习八 第8题】
40×10×20=8000(cm3)
答:这块长城砖的体积是8000 cm3 。
三、长方体和正方体
一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是 6 cm、4 cm、5 cm,正方体的棱长是多少厘米?它们的体积相等吗?
【选自教材P37 练习八 第9题】
正方体的棱长:(6+4+5)÷3 = 5(dm),
体积是 5 × 5 × 5 = 125(dm3)
长方体的体积是 6 × 4 × 5 = 120(dm3),
所以长方体和正方体的体积不相等,正方体的体积大。
三、长方体和正方体
茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
最多 6 盒,竖着放 4 盒,横着放 2 盒。
30×30×30÷(20×20×10)=6.75(盒)
【选自教材P37 练习八 第10题】
三、长方体和正方体
判断对错。
(1)一辆货车车厢所能容纳货物的体积,就是
这辆货车车厢的容积。 ( )
(2)一个药瓶里装了半瓶药水,这些药水的体
积就是药瓶的容积。 ( )
(3)有两个体积一样大的箱子,它们的容积一
定同样大。 ( )
√
×
×
三、长方体和正方体
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
三、长方体和正方体
一个长方体的油箱,从里面量长 5 dm,宽 4 dm,高 2 dm。这个油箱可以装多少升油?
5×4×2=40(dm3)
40 dm3=40 L
答: 这个油箱可以装汽油 40 L。
三、长方体和正方体
在横线上填写合适的容积单位。
一瓶墨水约 50____
一瓶洗手液约500___
“奋斗者”号载人潜水器载人舱的容积为3___
mL
mL
一台冰箱容积约229___
m3
L
【选自教材P40 练习九 第1题】
三、长方体和正方体
4 L=______mL 82 cm3=_____mL 4800 mL=_____L
2.4 L=______mL 35 dm3=______mL
500 mL=_____L
8.04 dm3=_____L=_______mL
785 mL=_____cm3=______dm3
4000
4.8
82
0.5
35000
2400
8.04
8040
785
0.785
【选自教材P40 练习九 第2题】
三、长方体和正方体
一桶 18 L的矿泉水相当于_____瓶 1500 mL 的矿泉水。
12
【选自教材P40 练习九 第3题】
三、长方体和正方体
一种微波炉,产品说明书上标明:炉腔内部尺寸400×225×300(单位:mm)。这个微波炉的容积是多少升?
400 mm=4 dm
225 mm=2.25 dm
300 mm=3 dm
4×2.25×3=27(dm3)
27 dm3=27 L
答:这个微波炉的容积是 27 L。
【选自教材P40 练习九 第4题】
三、长方体和正方体
为解决海岛上淡水缺乏的问题,某驻岛部队和当地居民共同修建了一个长 22 m、宽 10 m、深 1.8 m 的淡水蓄水池。这个蓄水池最多可蓄水多少立方米?
22×10×1.8 = 396(m3)
答:最多可蓄水 396 m3。
【选自教材P40 练习九 第5题】
三、长方体和正方体
一辆货车的车厢是长方体,从里面量长 3 m,宽 2.5 m,高 2 m。车厢的容积是多少立方米?
3×2.5×2=15(m3)
答:它的容积是 15 立方米。
【选自教材P40 练习九 第6题】
三、长方体和正方体
1. 1个水壶能装水2.5 L。“2.5L”指的是这个水壶的
( )。
A.体积 B.表面积 C.容积
2. 一个木箱能容纳40dm3的物体,这个木箱的体积
( )40dm3
A.大于 B.等于 C.小于
C
A
选一选。(将正确答案的序号填在括号里)
三、长方体和正方体
3.两个容器的体积相等,它们的容积( )。
A.可能不相等 B.一定不相等 C.一定相等
4.一个长方体水箱从里面量长0.6 m,宽0.4 m,高0.3m,
这个水箱可以装水( )L。
A.0.027 B.0.72 C.72
C
A
三、长方体和正方体
下图中珊瑚石的体积是多少?
8×8×( 7-6 )=64(cm3)
答:珊瑚石的体积是 64 cm3。
【选自教材P41 练习九 第7题】
三、长方体和正方体
将一块假山石放入一个盛有水的、底面积为 51 dm2 的长方体鱼缸中,完全浸没后,水面上升了 3 cm。这个假山石的体积有多大?
51×0.3=15.3(dm3)
3 cm=0.3 dm
答:假山石的体积为15.3dm3。
【选自教材P41 练习九 第8题】
三、长方体和正方体
在一个长 8 m、宽 5 m、高 2 m 的水池中注满水,然后把两条长 3 m、宽 2 m、高 4 m 的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×(4-2)×2=24(m3)
答:水池溢出的水的体积是 24 m3。
【选自教材P41 练习九 第9题】
三、长方体和正方体
把两个棱长为 1.5 dm 的正方体木块拼成一个长方体。这个长方体的体积、表面积分别是多少?如果是用 3 个正方体木块呢?
体积:1.5×1.5×1.5×2=6.75(dm3)
表面积:1.5×1.5×10=22.5(dm2)
体积:10.125 dm3
表面积:31.5 dm2
【选自教材P41 练习九 第10题】
三、长方体和正方体
右图是新疆吐鲁番酿制葡萄干的一种长方体晾房。其中一间从里面测量的底面积是 24.6 m2,高是 3 m。它的容积是多少呢?
24.6×3=73.8(m3)
答:它的容积是 73.8 m3。
【选自教材P41 练习九 第11题】
三、长方体和正方体
“冰雪大世界”每年用的冰大约能融化成 6 万立方米的水,这相当于多少个长 50 m、宽 25 m、深 1.2 m 的水池的蓄水量?
60000÷(50×25×1.2)= 40(个)
答:相当于 40 个这样的水池的蓄水量。
【选自教材P41 练习九 第12题】
三、长方体和正方体
求下图中大圆球的体积。
【选自教材P41 练习九 第13题】
你读到了哪些信息?要解决什么问题?
1个
+
1个 ,
水溢出12mL,
1个
+
4个 ,
水溢出24mL,
求大球的体积。
三、长方体和正方体
24 mL=24 cm3,12 mL=12 cm3
(24-12) ÷ 3=4(cm3)
12-4=8(cm3)
答:大球的体积是8cm3。
1个
+
1个 ,
水溢出12mL,
1个
+
4个 ,
水溢出24mL,
求大球的体积。
有一个装有一些水的长方体玻璃缸,从里面量长10 cm,宽 8 cm。往这个玻璃缸里放入一个柿子,水面上升了2cm(水淹没柿子且未溢出),这个柿子的体积是多少
10×8×2=160(cm3)
答:柿子的体积是160 cm3。
三、长方体和正方体
一个长方体玻璃容器,从里面量长和宽都是 2 dm ,里面
装有 5.6 L水, 将一个鹅卵石完全浸没在水中,水未溢出,
这时水深15 cm,这个鹅卵石的体积是多少?
5.6 L=5.6 dm3
15 cm=1.5 dm
2×2×1.5-5.6=0.4(dm3)
答:这个鹅卵石的体积是0.4 dm3。
三、长方体和正方体
求下图中一个小球的体积。(小球体积均相等)
20×16×(16-14)÷(6-1)=128(cm3)
答:小球的体积是128cm3。
三、长方体和正方体
长方体的长、宽、高都变为原来的 2 倍,它的表面积和体积分别发生了什么变化?你发现了什么规律?
长方体 长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
1 2 1 3
2 4 2 6
3 8 4 12
22
6
88
48
352
384
规律:如果长方体长、宽、高都变为原来的 2 倍,
它的表面积变为原来的 4 倍,体积变为原来的 8 倍。
【选自教材P43 练习十 第2题】
三、长方体和正方体
8×4.5×2 = 72(m3)
一个长方体鱼塘长 8 m,宽 4.5 m,深 2 m。这个鱼塘的容积是多少?
答:这个鱼塘的容积是72立方米。
【选自教材P43 练习十 第3题】
三、长方体和正方体
某古建筑景点定做了 25 个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米 18 元,这些宫灯的外饰面一共要花多少钱?
(66×20×4+46×80×4)×25
= 500000(cm2)
= 50(m2)
18×50 = 900(元)
答:这些宫灯的外饰面一共要花900元。
【选自教材P43 练习十 第4题】
三、长方体和正方体
选一选。(将正确答案的序号填在括号里)
1. 堆一个体积是1m3的大正方体,需要用体积是
1dm3的正方体木块( )个。
A.10 B.100 C.1000
C
三、长方体和正方体
2.一大桶矿泉水的净含量为 18 L ,相当于( )
瓶 600 mL 的小瓶矿泉水。
A.300 B.30 C.3
B
三、长方体和正方体
3. 一个正方体的棱长扩大到原来的 2 倍后体积
是 64 dm3 ,原来正方体的体积是( )dm3。
A.32 B.16 C.8
C
三、长方体和正方体
4.将两个长10 dm 、宽8 dm 、高5 dm 的长方体货
物包装在一起,至少要用( )dm2的包装纸。
A.520 B.600 C.680
A
三、长方体和正方体
修路队要给一段长200 m,宽18 m的水泥路面铺一层6cm厚的沥青,一共需要沥青多少方
(1方=1 m3)
6 cm = 0.06 m
200×18×0.06 = 216(m3)
216 m3= 216 方
答:一共需要沥青 216 方。
三、长方体和正方体
(1)(50×30+40×30)×2+50×40=7 400(平方厘米)。
答:需要玻璃7 400平方厘米。
(2)40升=40 000立方厘米,40 000÷(50×40)=20(厘米)。
答:水深大约20厘米。
(3)50×40×2.5=5 000(立方厘米)。
答:放入物体的体积一共是5 000立方厘米。
一个长方体玻璃鱼缸,长50厘米、宽40厘米、高30厘米。
(1)做这个鱼缸至少需要玻璃多少平方厘米?
(2)在鱼缸里注入40升水,水深大约多少厘米?
(3)再往水里放入鹅卵石、水草和鱼,测得水面上升了2.5厘米,求放入物体的体积一共是多少立方厘米?
三、长方体和正方体
一个长方体的容器(如图),里面的水深5 cm,把这个容器盖紧后竖放,使长10 cm、宽8 cm的面朝下,这时里面的水深是多少厘米?
20×10×5÷(10×8)
=12.5(厘米)。
答:这时里面的水深是12.5厘米。
三、长方体和正方体
2
3
分子:
表示取其中的几份。
分数线:
表示平均分。
分母:
表示平均分的份数。
四、分数的意义和性质
的分数单位是( ),
的分数单位是( )。
的分数单位是( ),
的分数单位是( ),
分母是几,分数单位就是几分之一。
四、分数的意义和性质
的分数单位是( ),
的分数单位是( ),
的分数单位是( ),
的分数单位是( ),
有( )个分数单位;
有( )个分数单位;
有( )个分数单位;
有( )个分数单位。
分子是几,就有几个分数单位。
1
2
3
5
四、分数的意义和性质
把下面每个图形都看作单位“1”,用分数表示各图中涂色部分的大小。
【选自课本P47 做一做 第1题】
四、分数的意义和性质
每个福娃是这排福娃的 。
2个冰墩墩是这排冰墩墩的 。
1
5
【选自课本P47 做一做 第2题】
2
5
四、分数的意义和性质
每个茶杯是这套茶杯的
每种颜色的跳棋是这盒跳棋的 。
一小杯液体是这瓶液体的
1
4
1
6
1
10
【选自课本P47 做一做 第3题】
四、分数的意义和性质
填一填。
1. 表示把单位“1”平均分成( )份,取其中
的( )份,它的分数单位是( )。
7
6
2. 4个 是( ),1里面有( )个 。
8
四、分数的意义和性质
把下面每个图形都看作单位“1”,用分数表示各图中涂色部分的大小。
8
3
7
5
4
3
8
5
四、分数的意义和性质
每个苹果是这些苹果的 。
5
1
每块饼干是这些
饼干的 。
8
1
四、分数的意义和性质
3盆鸡蛋是这些鸡蛋的 。
吃了的梨是这些梨的 。
4
3
6
2
四、分数的意义和性质
一盒蛋糕有12个(如图),
如果平均分给6个小朋友,
每人分得这盒蛋糕的 ,每人分得( )个;
如果平均分给2个小朋友,
每人分得这盒蛋糕的 ,每人分得( )个。
6
1
2
2
1
6
四、分数的意义和性质
按要求涂色。
涂上红色,其余的 涂上你喜欢的颜色。
2
3
涂上绿色,其余的 涂上你喜欢的颜色。
1
2
【选自课本P48 练习十一 第1题】
四、分数的意义和性质
1
3
4
一包饼干平均分给3人,每人分得 包。如果一包有12块,平均每人分得( )块。
【选自课本P48 练习十一 第2题】
四、分数的意义和性质
读出下面的分数,并写出每个分数的分数单位及分数单位的个数。
分 数:
分 数 单 位:
分数单位的个数:
( )个
( )个
( )个
( )个
( )个
1
6
1
7
1
2
1
15
4
1
18
11
1
100
7
【选自课本P48 练习十一 第3题】
四、分数的意义和性质
上面两条直线中,每条直线上的最小刻度用分数表示分别是多少 它们分别是哪些分数的分数单位
0
1
0
1
用直线上的点表示下面各分数。
【选自课本P48 练习十一 第4题】
四、分数的意义和性质
0
1
0
1
(1)最小刻度是 ,是 , , 的分数单位。
1
4
1
4
2
4
3
4
(2)最小刻度是 ,是 , , , , 的分数单位。
1
6
1
6
2
6
3
6
4
6
5
6
用直线上的点表示下面各分数。
【选自课本P48 练习十一 第4题】
四、分数的意义和性质
(1)5个 组成( ), 由( )个
组成。
四、分数的意义和性质
(2)8个 组成1, 1里面有12个 。
1
8
12
填一填。
1. 地球陆地面积约地球总面积的 ,这里是把
( )看作单位“1”。
读作( ),它的分数
单位是( )。
地球总面积
一百分之二十九
四、分数的意义和性质
2. 里面有( )个 ,4个 是( ),
是3个( )。
7
3. 里面有( )个 分数单位 ,再添上( )
个这样的分数单位就是“1”。
3
5
选一选。(将正确答案的序号填在括号里)
1.下面的分数中,分数单位最小的是( )。
A.
B.
C.
D.
D
四、分数的意义和性质
2.把7个苹果平均分给4个小朋友,每个小朋友分
得这些苹果的( )。
A.
B.
C.
D.
C
填表。
3
7
4
7
63
四、分数的意义和性质
(1)把2个月饼平均分给3
人,每人分多少个?
(2)把5个月饼平均分给8人,
每人分多少个?
2÷3= (个)
5÷8= (个)
四、分数的意义和性质
被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线。
被除数
÷
除数
=
被除数
除数
除法是
一种运算
分数是一种数
a
÷
b
=
a
b
(b≠0)
相当于
相当于
相当于
分数与除法的关系
用分数表示下面各式的商。
24÷25= 16÷49=
2÷9= 11÷12=
【选自课本P51 练习十二 第3题】
四、分数的意义和性质
在括号里填上适当的数。
7÷13= =( )÷( )
( )÷7=
13
7
8
5
4
【选自课本P50 做一做 第1题】
四、分数的意义和性质
1kg葡萄干平均装在2个袋子里,每袋装多少千克?平均装在3个袋子里呢?(用分数表示。)
1÷2 = (kg)
1
2
1÷3 = (kg)
1
3
答:装2个袋子,每袋重 kg,装3个袋子,每袋重 kg。
【选自课本P51 练习十二 第1题】
四、分数的意义和性质
3÷4 = (m )
3
4
3÷5 = (m )
3
5
答:种4种花,每种花平均占地 平方米,种5种花,每种花平均占地 平方米。
3
4
3
5
一个3m2的花坛,种4种花,每种花平均占地多少平方米 种5种呢 (用分数表示。)
【选自课本P51 练习十二 第2题】
四、分数的意义和性质
填一填。
1.
7÷8=
( )
( )
( )÷9=
=( )÷( )
( )÷( )=
7
8
4
7
37
13
45
四、分数的意义和性质
2.
km表示把4 km平均分成( )份,取其中的
( )份,即 km;
也可以表示把1km平均分成( )份,取其中的
( )份,即 km。
( )
( )
( )
( )
9
1
9
4
9
4
9
4
四、分数的意义和性质
5
10
32
100
23
60
17
60
3.
四、分数的意义和性质
7
100
57
1000
500
1000
1
1000
四、分数的意义和性质
把一根2 m长的绳子平均分成5段,每段长多少米?平均分成6段呢?(用分数表示。)
2÷5=
(m)
2÷6=
(m)
答:平均分成5段,每段长 米,
平均分成6段,每段长 米。
四、分数的意义和性质
7 dm =
( )
( )
m
9
10
30
10
133
1000
7
10
56
100
53
1000
23
1000
13
60
48
100
9 cm =
( )
( )
dm
30 cm =
( )
( )
dm
133 dm =
( )
( )
m3
56 cm =
( )
( )
dm
53 mL =
( )
( )
L
23 kg =
( )
( )
t
13 秒 =
( )
( )
分
48 公顷 =
( )
( )
平方千米
【选课课本P51 练习十二 第4题】
动物园里有大象9头,金丝猴4只。金丝猴的数量是大象的几分之几?
答:金丝猴的数量是大象的 。
【选课课本P50 做一做 第2题】
四、分数的意义和性质
81个月球和1个地球的质量相等。月球质量是地球质量的几分之几?
【选课课本P51 练习十二 第5题】
答:月球的质量是地球质量的 。
1
81
四、分数的意义和性质
4月23日是世界读书日。这一天,标价11元一本的《快乐数学》售价9元。
(1)这本书的售价是标价的几分之几?
答:这本书的售价是标价的 。
9
11
【选课课本P52 练习十二 第10题】
四、分数的意义和性质
问题:优惠的价格占原来标价的几分之几?
解答:11-9=2(元) 2÷11=
2
11
(2)你还能提出其他数学问题并解答吗?
4月23日是世界读书日。这一天,标价11元一本的《快乐数学》售价9元。
【选课课本P52 练习十二 第10题】
四、分数的意义和性质
五(1)班共有17幅书法作品参加学校的书法比赛,其中4幅作品从全校255幅参赛作品中脱颖而出获奖。
(1)五(1)班获奖作品占全班参赛作品的几分之几
(2)五( 1 )班参赛作品占全校参赛作品的几分之几
两小题中的单位“1”
分别是什么
【选课课本P52 练习十二 第11题】
四、分数的意义和性质
(1)单位“1”是全班的参赛作品。
4
17
4
÷
17
=
(2)单位“1”是全校的参赛作品。
17
255
17
÷
255
=
填空。
(1) 年有( )个月, 年有( )个月。
(2) 一年中,大月的月份占 ,小月的月份占
。
(3) 一个星期中,周六、周天两天占一周的 。
6
9
7
12
2
7
【选课课本P52 练习十二 第13题】
4
12
四、分数的意义和性质
1÷5 =
1
5
答:桌子的宽度是这颗纺锤树最粗部分直径的 。
1
5
一棵纺锤树最粗部分的直径为5m,一张桌子的宽为1 m。桌子的宽度是这棵纺锤树最粗部分直径的几分之几
纺锤树的根系发达,树干里可以贮存很多水分。
四、分数的意义和性质
50+25 = 75(头)
16÷75 =
25
50
某农场有50头大牛和25头小牛,还有16只羊。
(1)大牛的头数是小牛的多少倍?
(2)小牛的头数是大牛的几分之几?
(3)你还能提出其他数学问题并解答吗?
(1)50÷25 = 2
(3)羊的只数是牛的几分之几?
(2)25÷50 =
25
50
(提问不唯一)
四、分数的意义和性质
5÷6 = (m)
5
6
答:平均每人分 米。
5
6
老师买了5m的红绸带,平均分给表演节目的6名女生。每人分得几米?(用分数表示)
四、分数的意义和性质
1÷15 = (km)
1
15
答:平均每分钟走 千米。
1
15
小明15分钟走了1km的路,平均每分钟走多少千米?(用分数表示。)
四、分数的意义和性质
带分数
分数
真分数
假分数
<1
≥1
, ,
···
, ,
···
,
···
(分子<分母)
(分子≥分母)
(分子不是分母的整数倍)
分子比分母小的分数叫作真分数,真分数小于1。
单位“1”
单位“1”
单位“1”
<1
<1
<1
四、分数的意义和性质
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
=1
>1
>1
分子大于或等于分母的分数叫作假分数,
假分数大于或等于1。
四、分数的意义和性质
单位“1”
单位“1”
单位“1”
单位“1”
单位“1”
1
2
+
+
读作:
“二又五分之一”
读作:
“一又四分之三”
像这样由整数和真分数合成的数叫作带分数。
由几个圆组成?
由几个圆组成?
2
0
1
下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
(真)
(真)
(真)
(假)
(假)
(假)
(假)
【选自课本P54 做一做 第1题】
单位“1”
四、分数的意义和性质
判断下面的说法是否正确,并说一说你的理由。
(1)我吃了一个西瓜的 。
(2)爷爷把一块菜地的 种了西红柿, 种了茄子,
种了辣椒。
(3)一块巧克力,我吃了 ,表哥吃了 。
不对
不对
对
【选自课本P55 练习十三 第2题】
四、分数的意义和性质
把一个图形看作单位“1”,用分数表示图中的涂色部分,再读一读。
读作:四分之七
读作:六分之二十三
【选自课本P55 练习十三 第1题】
四、分数的意义和性质
(1)写出分母是7的所有真分数。
(2)写出分子是7的所有假分数。
(1)
1
7
2
7
3
7
4
7
5
7
6
7
(2)
7
1
7
2
7
3
7
4
7
5
7
6
7
7
【选自课本P56 练习十三 第8题】
四、分数的意义和性质
填一填。
1.分数 ,当x( )时,它是真分数;
当x( )时 ,它是大于1的假分数,
当x( )时 ,它是等于1的假分数,
当x( )时, 无意义。
>9
=9
<9
=0
四、分数的意义和性质
2.如果 是真分数, 是假分数,那么n可以取的
数有( )个。
6
四、分数的意义和性质
7÷4=1……3
=
①假分数化成带分数时,分数的大小不变,分数单位也不变,所以真分
数的分母不变。
②如果分子是分母的整数倍,这个假分数表示的就是一个整数;
如果分子不是分母的整数倍,带分数就是整数与真分数合成的数。
四、分数的意义和性质
把下面的假分数化成整数或带分数。
15
8
5
21
50
43
12
69
20
30
15
9
2
7
3
2
7
1
2
1
3
5
5
5
9
3
7
12
3
9
20
【选自课本P54 做一做 第2题】
四、分数的意义和性质
(1) 3个人平均分,每人分 杯,也就是____杯。
(2) 2个人平均分,每人分______杯。
3
3
1
【选自课本P55 练习十三 第3题】
有3杯水。
四、分数的意义和性质
8
5
12
5
15
5
18
5
1
5
1
4
5
2
3
5
3
在直线上面的 里填上适当的假分数,直线下面的 里填上适当的带分数。
【选自课本P55 练习十三 第5题】
四、分数的意义和性质
1
2
3
1
3
2
把一个图形看作单位“1”,用分数表示各图中的涂色部分。
【选自课本P55 练习十三 第6题】
四、分数的意义和性质
<
<
>
=
带分数
在○里填上“>”“<”“=”。
你认为带分数和假分数哪个更容易看出数的大小
【选自课本P56 练习十三 第9题】
四、分数的意义和性质
10÷3= (天)= 3 (天)
10
3
1
3
答:这板药能吃3 天。
1
3
一板药共10粒,每天早、中、晚各吃1粒。这板药能吃多少天 (用带分数表示。)
【选自课本P55 练习十三 第4题】
四、分数的意义和性质
熊的冬眠时间约是睡鼠的几分之几?睡鼠的冬眠时间约是熊的几分之几?
7÷5=
7
5
5÷7=
5
7
【选自课本P56 练习十三 第7题】
5
7
7
5
四、分数的意义和性质
先涂色表示下面的分数,再比较它们的大小。
<
=
四、分数的意义和性质
下面每组中的两个分数是否相等?相等的在括号里画“√”,不相等的画“×”。
和 ( )
和 ( )
和 ( )
和 ( )
√
×
√
×
四、分数的意义和性质
五(1)班 的同学参加舞蹈小组, 的同学参加了书法小组。参加哪个小组的人数多?
2
5
=
2×2
5×2
=
4
10
因为 ,所以参加两个小组的人数相等。
四、分数的意义和性质
下列分数中哪些在直线上能用同一个点表示?把它们在直线上表示出来。
0
1
2
四、分数的意义和性质
把下面的分数化成分母是10而大小不变的分数。
3
2
=
3×5
2×5
=
15
10
6
20
=
6÷2
20÷2
=
3
10
24
30
=
24÷3
30÷3
=
8
10
1
5
=
1×2
5×2
=
2
10
15
50
=
15÷5
50÷5
=
3
10
四、分数的意义和性质
( )
( )
( )
( )
涂色表示出与给定分数相等的分数。
2
6
2
8
四、分数的意义和性质
因为
( )
( )
÷
=
4
10
40
1
所以两个班做练习用的时间一样长。
如果一堂课40分钟,五(1)班做了10分钟的练习,五(2)班做练习的时间占整堂课的 。哪个班做练习用的时间长?
四、分数的意义和性质
布置板报。
哪些栏目的版面一样大?
四、分数的意义和性质
“知识海洋”、“生活乐园”和“科学园地”版面一样大。“历史足迹” 和“开心一刻”一样大。
2021年世界500强企业排行榜中,中国上榜企业数量达145家。中国上榜企业数量占世界500强的 ,也就是 。
29
四、分数的意义和性质
*一个分数的分母不变,分子乘3,这个分数的大小有什么变化?如果分子不变,分母除以5呢?
一个分数的分母不变,分子乘3,这个分数扩大3倍。如果分子不变,分母除以5,这个分数扩大5倍。
四、分数的意义和性质
8的因数
12的因数
1,2,4
3,6,
12
8
1、2、4是8和12公有的因数,叫做它们的公因数。其中,4是最大的公因数,叫做它们的最大公因数。
集合法
四、分数的意义和性质
怎样求 18 和 27 的最大公因数?
列举法
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
18和27的最大公因数是9。
分解质因数
18=2×3×3
27=3×3×3
18和27的最大公因数是9。
求下面各组数的最大公因数。
2和11 9和10
2的因数:1,2
11的因数:1,11
9的因数:1,3,9
10的因数:1,2,5,10
2和11的最大公因数是1
9和10的最大公因数是1
公因数只有1的两个数叫做互质数。
四、分数的意义和性质
18
27
3
6
9
3
2
3
依次用这两个数的公因数去除,直到最后得到的两个商互质为止,然后把公有的质因数相乘就是它们的最大公因数。
短除法
最大公因数乘半边
小亮家储藏室的长方形地面长16 dm,宽12 dm。如果用边长是整分米数的正方形地砖将储藏室的地面铺满(使用的地砖必须都是整块的),可以选择边长是几分米的地砖?边长最大是几分米?
四、分数的意义和性质
男生48人、女生36人分别站成若干排。要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
【选自课本P63 练习十五 第6题】
四、分数的意义和性质
48 和 36 的最大公因数是 12。
答: 每排最多有 12 人,这时男生有 4 排,女生有 3 排。
48÷12 = 4(排)
36÷12 = 3(排)
每排最多有12人。
在括号里写出各个分数中分子和分母的最大公因数。
( )
( )
( )
( )
( )
( )
1
4
18
3
7
11
【选自课本P63 练习十五 第4题】
四、分数的意义和性质
写出相邻两个数的最大公因数。
1
1
5
3
6
12
36
【选自课本P63 练习十五 第7题】
四、分数的意义和性质
(1)9和16的最大公因数是( )。
A.1 B.3 C.4 D.9
(2)48和60的最大公因数是( )。
A.4 B.6 C.12 D.36
把正确答案的序号填在括号里。
C
A
【选自课本P64 练习十五 第9题】
四、分数的意义和性质
(3)甲数是乙数的倍数,甲、乙两数的最大公因数是( )。
A.1 B.甲数 C.乙数 D.甲、乙两数的积
C
(1)两个数都是质数: ____ 和 ____。
(2)两个数都是合数: ____ 和 ____。
(3) 一个质数一个合数: ____ 和 ____。
按要求写出两个数,使它们的最大公因数是 1。
2
5
4
9
13
8
【选自课本P64 练习十五 第8题】
四、分数的意义和性质
有一张长方形纸,长70cm,宽50cm。如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?
10cm
【选自课本P63 练习十五 第5题】
四、分数的意义和性质
要把右面这些木棒截成同样长的若干段,不能有剩余,每段最长是多少厘米?
12、16 和 44 的最大公因数是 4 。
答: 每根小棒最长是 4 厘米。
【选自课本P64 练习十五 第11题】
四、分数的意义和性质
五(3)班同学买了64个苹果和96个梨去看望养老院的老人。这些水果正好可以平均分给养老院的老人,每人分得的苹果同样多,分得的梨也同样多,且都没有剩余。这个养老院最多有多少位老人
64和96的最大公因数是32,故这个养老院最多有32位老人。
四、分数的意义和性质
把一块长42 m,宽28 m 的长方形菜园划分成若干个面积相等的小正方形。小正方形的面积最大是多少
42和28的最大公因数是14,要使小正方形的面积最大,则边长应为14 m。
14 ×14=196(m2 )
四、分数的意义和性质
填空。
(1)10和15的公因数有 。
1、5
(2)14和49的公因数有 。
1、7
四、分数的意义和性质
找出下面每组数的最大公因数。
6和9 15和12 42和54
30和45 99和36 5和9
34和17 16和48 15和16
13和78
3
3
6
15
9
1
17
16
1
13
四、分数的意义和性质
(1)8和16的公因数有____________,最大因数是________。
(2)8和20的公因数有____________,最大因数是________。
(3)16和20的公因数有____________,最大因数是________。
(4)8、16和20的公因数有_________,最大因数是________。
1、2、4、8
8
1、2、4
4
1、2、4
4
1、2、4
4
四、分数的意义和性质
填空
16
32
( )
16
4
( )
=
=
=
( )
4
1
( )
=
( )
9
10
( )
=
=
( )
24
20
( )
=
=
2
3
8
8
2
2
6
15
16
30
四、分数的意义和性质
24
30
=
24÷2
30÷2
=
12
15
12
15
=
12÷3
15÷3
=
4
5
÷
÷
24
30
=
24 ( )
30 ( )
=
( )
( )
4
5
6
6
像这样,把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
四、分数的意义和性质
像 这样,分子和分母只有公因数1的分数叫做最简分数。
4
5
约分时,通常要约成最简分数。
仔细观察 ,它们之间有什么关系?
四、分数的意义和性质
9
9
4
2
4
1
3
5
下列分数中哪些是最简分数?把不是最简分数的化为最简分数。
、
、
、
、
是最简分数。
【选自课本P65 做一做 第1题】
四、分数的意义和性质
把上下两行相等的两个分数用线连起来。
4
6
3
7
2
5
6
8
3
9
9
21
3
4
1
3
2
3
10
25
【选自课本P65 做一做 第2题】
四、分数的意义和性质
右面两个圆的大小相同,蓝色部分和红色部分哪个大?为什么?
=
【选自课本P66 练习十六 第1题】
四、分数的意义和性质
下列分数中哪些没有化成最简分数?请把它们化成最简分数。
16
24
=
4
6
15
36
=
5
12
28
42
=
14
21
15
45
=
3
9
78
87
=
26
29
=
2
3
=
2
3
=
1
3
【选自课本P66 练习十六 第3题】
四、分数的意义和性质
观察下列分数的分子和分母,哪些有公因数2?哪些有公因数5?哪些有公因数3?
4
8
9
12
15
20
30
45
40
60
84
96
有公因数2
4
8
40
60
84
96
有公因数5
15
20
30
45
40
60
有公因数3
9
12
30
45
84
96
【选自课本P66 练习十六 第2题】
四、分数的意义和性质
把上下两行相等的两个分数用线连起来。
四、分数的意义和性质
先约分,再比较各组分数的大小。
四、分数的意义和性质
化简一个分数时,用2约了两次,用5
约了一次,得 。求原来的分数。
四、分数的意义和性质
把下列分数填入相应的圈里。
【选自课本P66 练习十六 第5题】
四、分数的意义和性质
兰兰拍了80张艺术照,其中有35张是她喜欢的。请你用最简分数表示出兰兰喜欢的照片和其他的照片分别占照片总数的几分之几。
35÷80=
7
16
喜欢的照片:
不喜欢的照片:
(80-35)÷80=
9
16
【选自课本P66 练习十六 第4题】
四、分数的意义和性质
先约分,再化成带分数。
15
12
20
12
77
21
70
32
90
80
150
60
【选自课本P67 练习十六 第9题】
四、分数的意义和性质
先约分,再化成带分数。
15
12
20
12
77
21
70
32
90
80
150
60
【选自课本P67 练习十六 第9题】
已知a=2×3×3×5,b=2×2×3×3×5,求a和b的公因数与最大公因数。
两个数共有的质因数或共有质因数的积,都是两个数的公因数。
a、b共有的质因数有2、3、3、5
2×3=6, 2×5=10,3×3=9,3×5=15,
2×3×3=18,2×3×5=30,3×3×5=45,
2×3×3×5=90
所以a、b的公因数有1、2、3、5、6、9、10、
15、18、30、45、90,最大公因数是90。
【选自课本P67 练习十六 第12题】
四、分数的意义和性质
下列分数中哪些在直线上能用同一个点表示?把它们在直线上表示出来。
1
0
3
12
6
24
7
14
4
16
3
6
【选自课本P66 练习十六 第6题】
四、分数的意义和性质
将48本练习本和64支铅笔平均分给若干名同学。如果练习本和铅笔都没有剩余,且保证分到练习本和铅笔的同学人数相同,最多能分给多少名同学
48和64的最大公因数是16。
最多能分给16名同学。
【选自课本P66 练习十六 第7题】
四、分数的意义和性质
小明的生活非常有规律,下面是他睡觉和起床的时间。
第一天晚上
第二天早上
小明睡觉的时间占全天的几分之几?
【选自课本P67 练习十六 第8题】
四、分数的意义和性质
10÷24 =
5
12
答: 他每天大约有 的时间处于睡眠状态。
5
12
第一天晚上
第二天早上
先约分,再比较各组分数的大小。
12
16
和
9
12
4
12
和
5
20
4
14
和
9
21
70
35
和
90
40
3
4
3
4
1
3
1
4
=
>
2
7
3
7
2
9
4
<
<
【选自课本P67 练习十六 第10题】
(1)以分米作单位,用分数分别表示长方形的长和宽。
4
5
分米
长:
3
5
分米
宽:
6cm
8cm
【选自课本P67 练习十六 第11题】
四、分数的意义和性质
4
3
长是宽的:8÷6=
3
4
宽是长的:6÷8=
(2)长方形的长是宽的几分之几?宽是长的几分之几?
6cm
8cm
【选自课本P67 练习十六 第11题】
可以用对角线将长方形平均分成两份,涂其中一份;也可以用对称轴将长方形平均分成两份,涂其中一份。
1
2
(3)涂出长方形面积的 ,你可以怎样涂?
6cm
8cm
【选自课本P67 练习十六 第11题】
*化简一个分数时,用2约了两次,用3约了一次,得 。求原来的分数。
3
8
3×2×2×3
8×2×2×3
=
36
96
36
96
答:原来的分数是 。
【选自课本P67 练习十六 第13题】
四、分数的意义和性质
填一填。
1.分母是8的真分数有( )个,其中最
简真分数有( )。
2.把 约分,可以用分子和分母的最大公
因数( )去约,结果是( )。
7
12
四、分数的意义和性质
3.在 和 中,与 相等的分数是( )。
4.一个最简真分数,分子与分母的和是20,这样
的分数有 ( )个。
5.一个最简真分数,分母与分子的积是24,这个
真分数可能是( )。
4
先约分,再化成带分数。
四、分数的意义和性质
路路家离学校有150 m,她从家里步行去学校,已经走了60 m。她已走的路程和剩下的路程分别占总路程的几分之几
四、分数的意义和性质
公倍数和最小公倍数:
两个数公有的倍数,叫作它们的公倍数。
其中最小的公倍数,叫作它们的最小公倍数。没有最大的公倍数。
我们也可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。
60 42
60=2×2×3×5
42=2×3×7
2
30
21
3
10
7
最小公倍数:
2×3×2×5×7
=420
最小公倍数:
2×3×10×7
=420
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公因数1为止
60 和 42
如果 a 是 b 的倍数,那么 a 是它们的最小公倍数。
如果 a 和 b 互质,那么它们的最小公倍数就是 ab。
找出下列每组数的最小公倍数。
8和10 6和15 6和9
4和15 1和7 4和10
40
30
18
60
7
20
【教材P71练习十七 第2题】
四、分数的意义和性质
下面每组数的公倍数中有没有36?有没有48?有没有84?
6和18 21和14 12和8 9和24
36
84
48
公倍数中没有36,48,84
【教材P71练习十七 第3题】
四、分数的意义和性质
按照从小到大的顺序,在100以内的数中找出6的倍数和10的倍数,再找出它们的公倍数和最小公倍数。
6的倍数:6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96。
10的倍数:10,20,30,40,50,60, 70,80,90。
6和10的公倍数是30,60,90;
最小公倍数
【教材P71练习十七 第1题】
求下列每组数的最小公倍数。
10 和 15
16 和 24
8 和 12
18 和 12
18 和 9
9 和 10
30
48
24
36
18
90
四、分数的意义和性质
选一选。 (将正确答案的序号填在括号里)
1.连续两个自然数( 0除外)的乘积一定是这两
个数的( ).
A.最大公因数 B.最小公倍数 C.公因数
B
四、分数的意义和性质
2.两个数的公倍数一定是这两个数( )。
A.倍数 B.因数 C.公倍数
A
3. a,b是不为 0 的自然数,已知 a ÷ b = 5,
那么 a 和 b 的最小公倍数是( )。
A.5 B.a C.b
B
4. 100 是 25 和 50 的 ( ).
A.最小公倍数 B. 最大公因数 C.公倍数
C
写出每组分数的两个分母的最小公倍数。
72
100
60
240
四、分数的意义和性质
判断下面的说法是否正确,并说一说你的理由。
(1)两个数的最小公倍数一定比这两个数都大。
(2)两个数的积一定是这两个数的公倍数。
√
×
【教材P71 练习十七 第4题】
四、分数的意义和性质
每只蝴蝶只落在自己数字的倍数的花朵上。哪朵花上两只蝴蝶都会停留?
24、48、72这3朵花上蝴蝶都会停留。
【教材P71 练习十七 第5题】
四、分数的意义和性质
在括号里写出每组分数的两个分母的最小公倍数。
和
和
和
【教材P71 练习十七 第7题】
( )
( )
( )
12
24
18
四、分数的意义和性质
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形 (用的地砖必须都是整块的), 正方形的边长可以是多少分米 最小是多少分米
四、分数的意义和性质
参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
四、分数的意义和性质
李阿姨家的月季每4天浇一次水,君子兰每6天浇一次水。李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日
【教材P71 练习十七 第6题】
四、分数的意义和性质
4和6的最小公倍数是12;
1+12=13(日)
答:下一次再给这两种花同时浇水应该是5月13日。
爸爸、妈妈带着小红和弟弟一起跑步。爸爸每跑一圈用时3分钟,妈妈每跑一圈用时4分钟,小红每跑一圈用时6分钟。
【教材P72 练习十七 第10题】
四、分数的意义和性质
(1)如果爸爸、妈妈在起点同时起跑,至少多少分钟后两人在起点再次相遇 此时爸爸、妈妈分别跑了多少圈
下面各组数有没有公因数2?有没有公因数3?有没有公因数5?
6和9 10和18 15和30 20和8
3
2
3、5
2
【教材P72 练习十七 第8题】
四、分数的意义和性质
3 路: 每 6 分钟发一次车
5 路: 每 8 分钟发一次车
3路和5路公共汽车的起点站相同。这两路公共汽车同时发车后,过多少分钟两路车第二次同时发车
24分钟
【教材P72 练习十七 第9题】
四、分数的意义和性质
* 36可能是哪两个数的最小公倍数?你能找出几组?
如36和1,36和2,36和3,36和4,36和6,36和9,36和12,36和 18;
4和9,4和18,9和12,12和18。共12组。
【教材P72 练习十七 第11题】
四、分数的意义和性质
五(1)班分组进行拔河比赛,不管是8人一组,还是10人一组,都刚好分完。五(1)班有多少人
8和10的公倍数有40,80,… 40<50,五(1)班有40人。
四、分数的意义和性质
体育馆站是6路和18路公共汽车的起点站,6路公共汽车每5分钟发一次车,18路公共汽车每6分钟发一次车。这两路公共汽车在6:00同时发车后,下一次同时发车是什么时候
5和6的最小公倍数是30,故下一次同时发车是6:30。
四、分数的意义和性质
,
,
①
②
分母相同
分子相同
比较分子,分子大的
分数就大。
比较分母,分母大的
分数就小。
四、分数的意义和性质
在 里填上“>”“<”或“=”。
5
7
3
7
7
16
11
16
3
5
3
4
4
9
4
5
<
<
<
<
11
21
13
21
19
25
9
25
10
19
10
13
15
17
15
22
<
>
<
<
四、分数的意义和性质
像这样,把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
异分母分数
同分母分数
分数的基本性质
与原分数相等
四、分数的意义和性质
在 中填上“>”“<”或“=”。
3
13
7
13
5
6
5
8
2
3
3
5
4
30
2
15
>
>
>
=
说一说:怎样比较分数的大小?
【教材P74 做一做 第1题】
四、分数的意义和性质
把下面每组中的两个分数通分。
2
3
和
1
5
3
4
和
5
8
2
3
=
10
15
1
5
=
3
15
3
4
=
6
8
5
6
和
8
15
4
7
和
6
11
5
6
=
25
30
8
15
=
16
30
4
7
=
44
77
6
11
=
42
77
【教材P74 做一做 第2题】
把下面每组中的两个分数通分。
5
6
和
7
8
3
7
和
2
9
5
6
=
20
24
7
8
=
21
24
3
7
=
27
63
4
9
和
7
18
3
8
和
5
9
2
9
=
14
63
4
9
=
8
18
3
8
=
27
72
5
9
=
40
72
【教材P74 做一做 第2题】
比较每组中两个分数的大小,再和同学交流一下你的方法。
8
9
5
6
1
3
3
7
2
5
3
10
5
8
7
10
<
<
>
<
【教材P75 练习十八 第2题】
四、分数的意义和性质
1.把异分母分数( )化成和( )相等的( )分数,叫作通分。
2.通分时选用的公分母一般是原来几个分母的( )。
3.通分的方法先求出原来几个分母的( )
然后把各分数分别化成用这个( )作分母的分数。
分别
最小公倍数
最小公倍数
最小公倍数
原来分数
同分母
四、分数的意义和性质
4.通分的依据( )。
分数的基本性质
5.通分的目的是把( )分母的分数化成( )分母的分数。
异
同
比较每组中两个分数的大小。
3
8
1
8
11
25
17
25
5
7
5
17
12
23
12
19
<
<
>
<
【教材P75 练习十八 第1题】
四、分数的意义和性质
=
4×( )
5×( )
=
( )
( )
4
5
把下面每组中的两个分数通分。
=
6×( )
7×( )
=
( )
( )
6
7
(1)
【教材P75 练习十八 第5题】
四、分数的意义和性质
=
9× ( )
10×( )
=
( )
( )
9
10
=
3×( )
4×( )
=
( )
( )
3
4
(2)
在 里填上“>”“<”或“=”。
2
3
5
6
5
12
5
11
19
20
14
15
13
16
3
2
>
>
>
>
【教材P76 练习十八 第8题】
四、分数的意义和性质
亚洲陆地面积约占全球陆地面积的,非洲和南美洲的陆地面积分别约占全球陆地面积的和。亚洲、非洲和南美洲这三个洲中,哪个洲的陆地面积最大 哪个最小
【教材P75 练习十八 第6题】
四、分数的意义和性质
3
10
3×5
10×5
=
=
15
50
1
5
1×10
5×10
=
=
10
50
3
25
3×2
25×2
=
=
6
50
15
50
,
,
,因为
>
10
50
>
6
50
,
所以
3
10
>
1
5
>
3
25
。亚洲的陆地面积最大,
南美洲的陆地面积最小。
把下面分数按从小到大的顺序排列起来。
4
5
11
12
5
6
4
3
7
10
1
2
1
2
<
7
10
<
4
5
<
5
6
<
11
12
<
4
3
【教材P76 练习十八 第9题】
四、分数的意义和性质
把下列分数填入相应的圈里。
大于
小于
【教材P75 练习十八 第3题】
四、分数的意义和性质
张叔叔和李叔叔参加工厂的技能比赛。张叔叔加工完所有零件的时,李叔叔加工完所有零件的。在这段时间里,谁的比赛成绩更好一些?
因为 = , = , < ,所以 < ,
在这段时间里,李叔叔的比赛成绩更好一些。
1
2
5
10
3
5
6
10
5
10
6
10
1
2
3
5
【教材P75 练习十八 第4题】
四、分数的意义和性质
五(1)班要为图书角选购一批新书,班长决定先作一个意向调查。下面是调查结果(每人只选一种)。
应该怎样选购图书?说一说你的理由。
课外读物种类
喜欢的人数占全班总人数的几分之几
科普类
童话类
历史类
7
12
1
6
1
4
【教材P76 练习十八 第7题】
四、分数的意义和性质
1
6
=
2
12
1
4
=
3
12
7
12
>
1
4
,
,
>
1
6
。
所以,应该多选购科普类图书,少选购童话类图书。
最大公因数
最大公因数和最小公倍数的积
两个数的积
最小公倍数
10和20
8和12
9和21
7和11
4.按要求填写下表,看看你有什么发现。
10
4
3
1
20
24
63
77
200
96
189
77
200
96
189
77
你能再举例验证自己的发现吗?
【教材P76 练习十八 第10题】
四、分数的意义和性质
你能写出一个比 大又比 小的分数吗?你是怎样找到这个分数的?你还能再找到两个这样的分数吗?
1
5
1
6
11
60
、
16
90
、
17
90
……(答案不唯一)
、
【教材P76 练习十八 第11题】
四、分数的意义和性质
填空。
(1)0.6表示 。0.09表示 。
(2)0.5表示 。
(3)0.006里面有( )个千分之一,它表示
( )分之( ),写成分数是 。
6
10
9
100
5
10
6
千
六
6
1000
四、分数的意义和性质
把0.7 、 、0.25 、 、 、
10
9
100
43
25
7
47
13
按从小到大的顺序排列起来。
10
9
﹦0.9
100
43
﹦0.43
25
7
﹦7÷25﹦0.28
﹦13÷47≈0.277
47
13
0.25
<
47
13
<
25
7
100
43
<
<
0.7
<
10
9
四、分数的意义和性质
填空
把0.25化成分数时,因为0.25是( )小数,所以就在1后面写( )个0作( ),把0.25去掉小数点作( ),最后是( )。
两位
2
分母
分子
四、分数的意义和性质
0.3
3
10
0.25
1
4
0.4
2
5
分别用小数和分数表示下面各图中涂色部分的大小。
【选自课本P77 练习十九 第1题】
四、分数的意义和性质
把相等的小数和分数用线连起来。
【选自课本P77 练习十九 第3题】
四、分数的意义和性质
把下面的小数化成分数,分数化成小数(除不尽的保留两位小数)。
0.2
0.4
0.56
0.76
0.375
1.625
四、分数的意义和性质
0.5625
0.35
0.049
1.2
0.22
0.17
1.(1) 0.8里面有8个( )分之一,表示( )分之( ),化成分数是 。
(2) 0.05里面有5个( )分之一,化成分数是 。
(3) 0.007里面有7个( )分之一,化成分数是 。
(4) 0.36里面有36个( )分之一,化成分数是 。
十
十
八
4
5
百
1
20
千
7
1000
百
9
25
【选自课本P78 练习十九 第2题】
四、分数的意义和性质
把下列各数按从大到小的顺序排列起来。
【选自课本P79 练习十九 第8题】
四、分数的意义和性质
猎豹的速度是小汽车速度的多少倍 小汽车的速度是猎豹速度的几分之几
【选自课本P78 练习十九 第4题】
答:猎豹的速度是小汽车速度的1.55倍,
小汽车的速度是猎豹速度的 。
四、分数的意义和性质
小林从学校走回家要花25分钟,小东从学校走回家要花 小时。如果他们两人的行走速度相同,谁家离学校远些
【选自课本P79 练习十九 第10题】
四、分数的意义和性质
0.31
0.08
0.23
0.44
0.83
0.22
1.15
把下面的分数化成小数(除不尽的保留两位小数)。
【选自课本P78 练习十九 第5题】
四、分数的意义和性质
在 里填上适当的小数,在 里填上适当的分数。
【选自课本P79 练习十九 第6题】
四、分数的意义和性质
用小数表示 用分数表示
40cm ( )m ( )m
150g ( )kg ( )kg
125cm2 ( )dm2 ( )dm2
3680dm3 ( )m3 ( )m3
在括号里填上适当的数。
【选自课本P79 练习十九 第7题】
李阿姨平均每秒打0.9个字,王叔叔平均每秒打 个字。谁打字快些?
【选自课本P79 练习十九 第9题】
四、分数的意义和性质
下面的分数与小数的互化是否正确?
四、分数的意义和性质
下面这些分数中哪些可以化成有限小数?
√
√
√
√
√
判断前看分数是不是最简分数
把最简分数的分母分解质因数:
8=2×2×2
40=2×2×2×5
21=3×7
30=2×3×5
四、分数的意义和性质
1.
( )>( )>( )>( )
2.
( )<( )<( )<( )
四、分数的意义和性质
解决问题。
一块正方形布料,既可以裁成若干条边长是8cm的方巾,也可以裁成若干条边长是10 cm的方巾,且都没有剩余。这块正方形布料的边长至少是多少厘米
四、分数的意义和性质
因为8和10的最小公倍数是40。
答:这块正方形布料的边长至少是40厘米。
8 cm
10 cm
把一根2m长的木条锯成同样长的4段,每段是这根木条的 ,每段长
( )÷ ( )= ( )m = m。
【选自课本P81 练习二十 第1题】
4
0.5
2
1
4
1
2
( )
( )
( )
( )
四、分数的意义和性质
【选自课本P82 练习二十 第2题】
判断下面的说法是否正确,并说一说你的理由。
(1)分数的分母越大,它的分数单位就越小。( )
(2)分数都比整数小。 ( )
(3)假分数的分子都比分母小。 ( )
×
√
×
假分数比整数大或相等
假分数的分子可能大于或等于分母
四、分数的意义和性质
(5)分子和分母的公因数只有1的分数是最简分数。
( )
(4)如果 b 是 a 的2倍(a,b为非零自然数),那么 a、b 的最大公因数是a ,最小公倍数是b 。 ( )
√
√
在横线上填写适当的分数。
【选自课本P82 练习二十 第4题】
25cm= ______m 36dm2 = ______m2
600g= ______kg 750mL = ______L
0.28dm= ______dm 258cm3 = ______ dm3
四、分数的意义和性质
在 里填上“>”“<”或“=”。
5
13
8
13
5
7
5
11
4
5
7
8
2
9
1
6
<
<
<
<
【选自课本P82 练习二十 第6题】
四、分数的意义和性质
你听过“冰山一角”的说法吗 冰山露在水面上的只是它的一小部分,大部分隐藏在水面下。假设一座冰山的体积是1000m3,它露在水面上的体积是100m3。冰山露在水面上的体积占总体积的 ,水面下的体积占总体积的 。
10
1
10
9
【选自课本P81 练习二十 第3题】
四、分数的意义和性质
一座喷泉由内外两层构成。外层每10分钟喷水一次,内层每6分钟喷水一次。12:45同时喷过一次水后,下次同时喷水是几时几分
6和10的最小公倍数是30。
12:45过30分是13:15
答:下次同时喷水的时间是13:15。
四、分数的意义和性质
可以怎样填?
第一题可以填: 、 、 、…
第二题可以填: 、 、 、…
【选自课本P82 练习二十 第11题】
四、分数的意义和性质
48和54的最大公因数是6。
答:每组最多有6人。
五、六年级学生参加学校大扫除,五年级来了48人,六年级来了54人。如果把两个年级的学生分别分成若干小组,要使两个年级每个小组的人数相同,每组最多多少人
【选自课本P81 练习二十 第5题】
四、分数的意义和性质
某学校五年级学生一共有150人,体质健康测试优良的为60人。其中五(1)班有38人,体质健康测试优良的为19人。五(1)班同学体质健康测试优良情况和五年级的总体情况相比怎么样
60 ÷ 150 = 19 ÷ 38 =
因为 , = ,所以 。
答:五(1)班班同学体质健康测试优良情况和五年级的总体情况相比稍好一些。
【选自课本P82 练习二十 第7题】
四、分数的意义和性质
(1) 3÷5 =
文文的纸飞机飞了5m,小刚的飞了4m,兰兰的飞了3m。
(1)兰兰的纸飞机飞的距离是文文的几分之几?
(2)你还能提出其他数学问题并解答吗?
四、分数的意义和性质
(2)答案不唯一
小刚的纸飞机飞的距离是文文的几分之几?
文文的纸飞机飞了5m,小刚的飞了4m,兰兰的飞了3m。
(1)兰兰的纸飞机飞的距离是文文的几分之几?
(2)你还能提出其他数学问题并解答吗?
【选自课本P82 练习二十 第9题】
果农准备将一批石榴进行分装。如果每8个装一盒,会剩下3个;如果每9个装一盒,也会剩下3个。这批石榴至少有多少个
8和9的最小公倍数是72
72+3=75(个)
答:这批石榴至少有75个。
四、分数的意义和性质
1. 4 的分数单位是( ),它有( )个
这样的分数单位。
2. 把5个苹果平均分给8个小朋友,每人分得这
些苹果的 ,每人分得( )个。
填一填。
( )
( )
32
8
1
四、分数的意义和性质
3.分母是10的最简真分数的和是( )。
4.在横线上填写适当的分数。
26cm=_____m
35dm2=_____m2
400g=_____kg
150mL=_____L
850cm3=_____dm3
15分=_____时
2
同课章节目录
