数学广角——找次品(课件)-五年级下册数学人教版(共30张PPT)
文档属性
| 名称 | 数学广角——找次品(课件)-五年级下册数学人教版(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第八单元 数学广角
——找次品
人教版·数学·五年级·下册
教学目标
1、初步认识“找次品”这类问题的基本解决手段和方法。
2、通过观察、猜想、试验、推理等活动,体会解决问题的策略的多样性及运用优化的方法解决问题的有效性。
3、感受到数学在日常生活的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,初步培养学生的应用意识和解决问题的能力。
少了3片的那瓶钙片的质量有什么特点?
1
有3瓶钙片,其中1瓶少了3片,看作次品。
你能设法把它找出来吗?
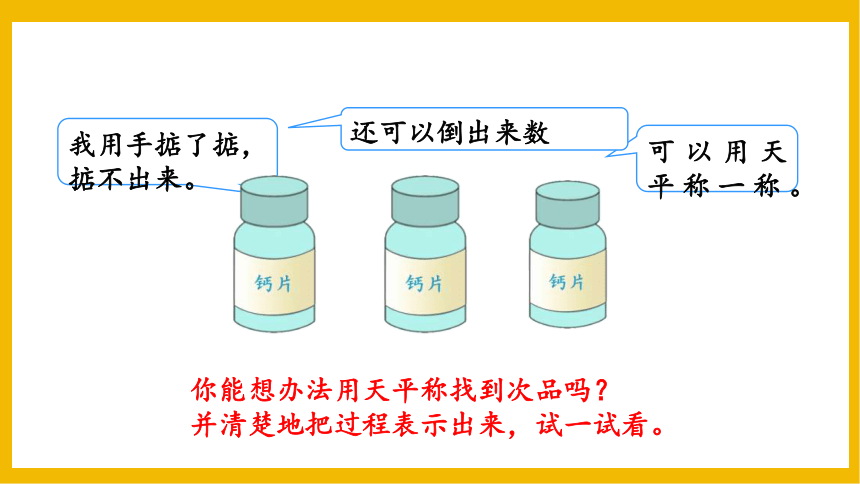
我用手掂了掂,掂不出来。
可以用天平称一称。
还可以倒出来数
你能想办法用天平称找到次品吗?
并清楚地把过程表示出来,试一试看。
方法一
一瓶一瓶地称,最轻的就是少了的那一瓶。
最轻的这瓶是次品。
要称三次。
利用天平平衡原理称量推理。
两瓶正品质量一样,天平平衡了,剩下的这瓶就是次品。
次品
方法二
次品比正品轻,天平不平衡,托盘向上的这瓶就是次品。
次品
利用天平平衡原理称量推理。
方法二
我们用 代表钙片,
3瓶钙片可表示为
1
2
3
平衡
不平衡
需要称____次。
1
可以这样记录。
1
2
, 是次品。
3
提示:
尽管天平只有2个托盘,但托盘外的第3个物品也参与到比较之中,所以天平可一次性比较出3个物品的质量。
次品
次品
(1)用天平找次品,并不一定要通过天平称出具体质量,利用天平的平衡原理,通过推理也能找出次品。
(2)用天平找次品,并不需要称量所有物品,关键是利用天平的平衡原理,判断次品是否出现在托盘上。
次品
次品
1
2
3
平衡
不平衡
需要称____次。
1
1
2
, 是次品。
3
(3)用直观图示的方式可以表示找次品的过程,说明解决找次品问题并不真的需要用天平来称量。关键是利用天平的平衡原理,通过推理来确定次品。
(3)从3个物品中找次品的基本思路:用天平称一次(可假想),然后根据天平称量的结果(平衡还是不平衡)来判断出次品是否在托盘上。也就是通过推理,确定次品是3个中的哪一个。
用天平从3个外形相同的物品中找其中1个次品的方法。
先任取其中2个物品,
如果天平平衡,次品是剩下的一个,
如果天平不平衡,次品是称的两个中的一个
(根据次品的特点轻重确定)。
称一次就能找到次品
8 个零件里有 1 个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
运用优化策略解决问题
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
2
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的6瓶中,
还要再称3次。
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的4瓶中,
还要再称2次。
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的2瓶中,
还要再称1次。
1
2
3
4
5
6
7
8
不平衡
还要再称1次
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
记录单
每次每边放的个数 分成的份数 至少要称的次数
1
8(1,1,1,1,1,1,1,1)
4
2
8(2,2,2,2)
3
3
8(3,3,2)
2
4
8(4,4)
3
(1)表中哪种方法需要称的次数最少?
观察完成的表格,你发现了什么?
第3种方法,物体分成三份。
(2)如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?你是怎么称的?
方法一
把9个零件平均分成3份,每份3个,先在天平两端各放3个称一次。
9
(
3
3
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的3个当中。
(
1
1
,1)
2次
(
1
1
,1)
2次
至少称2次
方法二
把9个零件分成3份(4,4,1),先在天平两端各放4个称一次。
9
(
4
4
,1)
平衡,另外1个是次品。
不平衡,称重的一端的4个。
1次
(
2
2
,1)
3次
至少称3次
(
1
1
)
不平衡,称重的一端的2个。
平衡,另外1个是次品。
(2)如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?你是怎么称的?
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系?
(2)怎样分找出次品需要称的次数最少?
把9个零件平均分成3份,找出次品需要的次数最少。
分成的份数越少,分的方法越平均,找出次品所要称的次数越少。
每次每边放的个数 分成的份数 要称的次数
4,4,1 3 3
3,3,3 3 2
2,2,2,2,1 5 3
1,1,1,1,1,1,1,1,1 9 4
(3)你能发现什么?用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
10个零件分成 3 份(3,3,4),则至少称 3次可以保证找出这个次品。
11个零件分成 3 份(4,4,3),则至少称3次可以保证找出这个次品。
研究更多的零件,验证规律是否正确。
10个零件
(3,3,4)
不平衡
称有次品的3个(1,1,1)
3次
2次
天平两边各放3个
天平两边各放1个
平衡 称剩下的2个
(1,1)
不平衡
找到次品
2次
平衡 称剩下的4个
(1,1,2)
11个零件
(4,4,3)
不平衡
称有次品的4个
(1,1,2)
3次
2次
平衡 称剩下的3个(1,1,1)
天平两边各放4个
平衡 称剩下的2个(1,1)
不平衡
找到次品
2次
天平两边各放1个
归纳总结:
找次品的最佳策略:
一是把物体分成3份;
二是每份数量尽量平均。
用天平找次品时,所测物品数目与测试的次数有以下关系: (只含一个次品,已知次品比正品重或轻。)
要辨别的物品数目 保证能找出次品需要测的次数
2~3 4~9 10~27 28~81 82~243 ······ 1
2
3
4
5
······
规律:小于或等于 3n 个物体中有一个次品,
至少需要称 n 次才能保证找出次品。
随堂练习
1.一箱糖果有12袋,其中11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
次品在剩下的一份中,取其中两包进行称量
平均分成3份(4,4,4)
次品在较轻的一份中,取其中两包进行称量
平衡
不平衡
次品在这两包中,较轻的是次品
平衡
不平衡
平衡
不平衡
次品在剩下的两包中,对其进行称量,较轻的是次品
次品在这两包中,较轻的是次品
次品在剩下的两包中,对其进行称量,较轻的是次品
2.有13袋薯片,其中有12袋质量相同,另外有1袋质量不足,轻一些。至少称几次能保证找出这袋来?(请你试着用图表示称的过程)
13袋薯片
(5,5,3)
3次
天平两边各放5个
剩下3袋糖果(1,1,1)
平衡
不平衡
剩下的1个是次品
2次
较轻的糖果(2,2,1)
天平两边各放2个
平衡
不平衡
较轻的袋糖果(1,1)
至少称3次能保证找出这袋来
2次
这节课你们都学会了哪些知识?
2.要分得尽量平均,能够平均分的就平均分,不能平均分的,也应该使最多的1份与最少的1份相差1。
1.把待测物品分成3份;
找次品的最优方法:
第八单元 数学广角
——找次品
人教版·数学·五年级·下册
教学目标
1、初步认识“找次品”这类问题的基本解决手段和方法。
2、通过观察、猜想、试验、推理等活动,体会解决问题的策略的多样性及运用优化的方法解决问题的有效性。
3、感受到数学在日常生活的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,初步培养学生的应用意识和解决问题的能力。
少了3片的那瓶钙片的质量有什么特点?
1
有3瓶钙片,其中1瓶少了3片,看作次品。
你能设法把它找出来吗?
我用手掂了掂,掂不出来。
可以用天平称一称。
还可以倒出来数
你能想办法用天平称找到次品吗?
并清楚地把过程表示出来,试一试看。
方法一
一瓶一瓶地称,最轻的就是少了的那一瓶。
最轻的这瓶是次品。
要称三次。
利用天平平衡原理称量推理。
两瓶正品质量一样,天平平衡了,剩下的这瓶就是次品。
次品
方法二
次品比正品轻,天平不平衡,托盘向上的这瓶就是次品。
次品
利用天平平衡原理称量推理。
方法二
我们用 代表钙片,
3瓶钙片可表示为
1
2
3
平衡
不平衡
需要称____次。
1
可以这样记录。
1
2
, 是次品。
3
提示:
尽管天平只有2个托盘,但托盘外的第3个物品也参与到比较之中,所以天平可一次性比较出3个物品的质量。
次品
次品
(1)用天平找次品,并不一定要通过天平称出具体质量,利用天平的平衡原理,通过推理也能找出次品。
(2)用天平找次品,并不需要称量所有物品,关键是利用天平的平衡原理,判断次品是否出现在托盘上。
次品
次品
1
2
3
平衡
不平衡
需要称____次。
1
1
2
, 是次品。
3
(3)用直观图示的方式可以表示找次品的过程,说明解决找次品问题并不真的需要用天平来称量。关键是利用天平的平衡原理,通过推理来确定次品。
(3)从3个物品中找次品的基本思路:用天平称一次(可假想),然后根据天平称量的结果(平衡还是不平衡)来判断出次品是否在托盘上。也就是通过推理,确定次品是3个中的哪一个。
用天平从3个外形相同的物品中找其中1个次品的方法。
先任取其中2个物品,
如果天平平衡,次品是剩下的一个,
如果天平不平衡,次品是称的两个中的一个
(根据次品的特点轻重确定)。
称一次就能找到次品
8 个零件里有 1 个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
运用优化策略解决问题
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
2
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的6瓶中,
还要再称3次。
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的4瓶中,
还要再称2次。
1
2
3
4
5
6
7
8
还要再称1次
平衡
不平衡
在余下的2瓶中,
还要再称1次。
1
2
3
4
5
6
7
8
不平衡
还要再称1次
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
记录单
每次每边放的个数 分成的份数 至少要称的次数
1
8(1,1,1,1,1,1,1,1)
4
2
8(2,2,2,2)
3
3
8(3,3,2)
2
4
8(4,4)
3
(1)表中哪种方法需要称的次数最少?
观察完成的表格,你发现了什么?
第3种方法,物体分成三份。
(2)如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?你是怎么称的?
方法一
把9个零件平均分成3份,每份3个,先在天平两端各放3个称一次。
9
(
3
3
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的3个当中。
(
1
1
,1)
2次
(
1
1
,1)
2次
至少称2次
方法二
把9个零件分成3份(4,4,1),先在天平两端各放4个称一次。
9
(
4
4
,1)
平衡,另外1个是次品。
不平衡,称重的一端的4个。
1次
(
2
2
,1)
3次
至少称3次
(
1
1
)
不平衡,称重的一端的2个。
平衡,另外1个是次品。
(2)如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?你是怎么称的?
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系?
(2)怎样分找出次品需要称的次数最少?
把9个零件平均分成3份,找出次品需要的次数最少。
分成的份数越少,分的方法越平均,找出次品所要称的次数越少。
每次每边放的个数 分成的份数 要称的次数
4,4,1 3 3
3,3,3 3 2
2,2,2,2,1 5 3
1,1,1,1,1,1,1,1,1 9 4
(3)你能发现什么?用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
10个零件分成 3 份(3,3,4),则至少称 3次可以保证找出这个次品。
11个零件分成 3 份(4,4,3),则至少称3次可以保证找出这个次品。
研究更多的零件,验证规律是否正确。
10个零件
(3,3,4)
不平衡
称有次品的3个(1,1,1)
3次
2次
天平两边各放3个
天平两边各放1个
平衡 称剩下的2个
(1,1)
不平衡
找到次品
2次
平衡 称剩下的4个
(1,1,2)
11个零件
(4,4,3)
不平衡
称有次品的4个
(1,1,2)
3次
2次
平衡 称剩下的3个(1,1,1)
天平两边各放4个
平衡 称剩下的2个(1,1)
不平衡
找到次品
2次
天平两边各放1个
归纳总结:
找次品的最佳策略:
一是把物体分成3份;
二是每份数量尽量平均。
用天平找次品时,所测物品数目与测试的次数有以下关系: (只含一个次品,已知次品比正品重或轻。)
要辨别的物品数目 保证能找出次品需要测的次数
2~3 4~9 10~27 28~81 82~243 ······ 1
2
3
4
5
······
规律:小于或等于 3n 个物体中有一个次品,
至少需要称 n 次才能保证找出次品。
随堂练习
1.一箱糖果有12袋,其中11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
次品在剩下的一份中,取其中两包进行称量
平均分成3份(4,4,4)
次品在较轻的一份中,取其中两包进行称量
平衡
不平衡
次品在这两包中,较轻的是次品
平衡
不平衡
平衡
不平衡
次品在剩下的两包中,对其进行称量,较轻的是次品
次品在这两包中,较轻的是次品
次品在剩下的两包中,对其进行称量,较轻的是次品
2.有13袋薯片,其中有12袋质量相同,另外有1袋质量不足,轻一些。至少称几次能保证找出这袋来?(请你试着用图表示称的过程)
13袋薯片
(5,5,3)
3次
天平两边各放5个
剩下3袋糖果(1,1,1)
平衡
不平衡
剩下的1个是次品
2次
较轻的糖果(2,2,1)
天平两边各放2个
平衡
不平衡
较轻的袋糖果(1,1)
至少称3次能保证找出这袋来
2次
这节课你们都学会了哪些知识?
2.要分得尽量平均,能够平均分的就平均分,不能平均分的,也应该使最多的1份与最少的1份相差1。
1.把待测物品分成3份;
找次品的最优方法:
