2024北京九中高二4月月考数学试题(PDF版含解析)
文档属性
| 名称 | 2024北京九中高二4月月考数学试题(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 00:00:00 | ||
图片预览




文档简介
2024北京九中高二4月月考
数
学
2024.4
(考试时间120分钟满分150分)
一、单选题(共40分)
1.(本题4分)从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有()个.
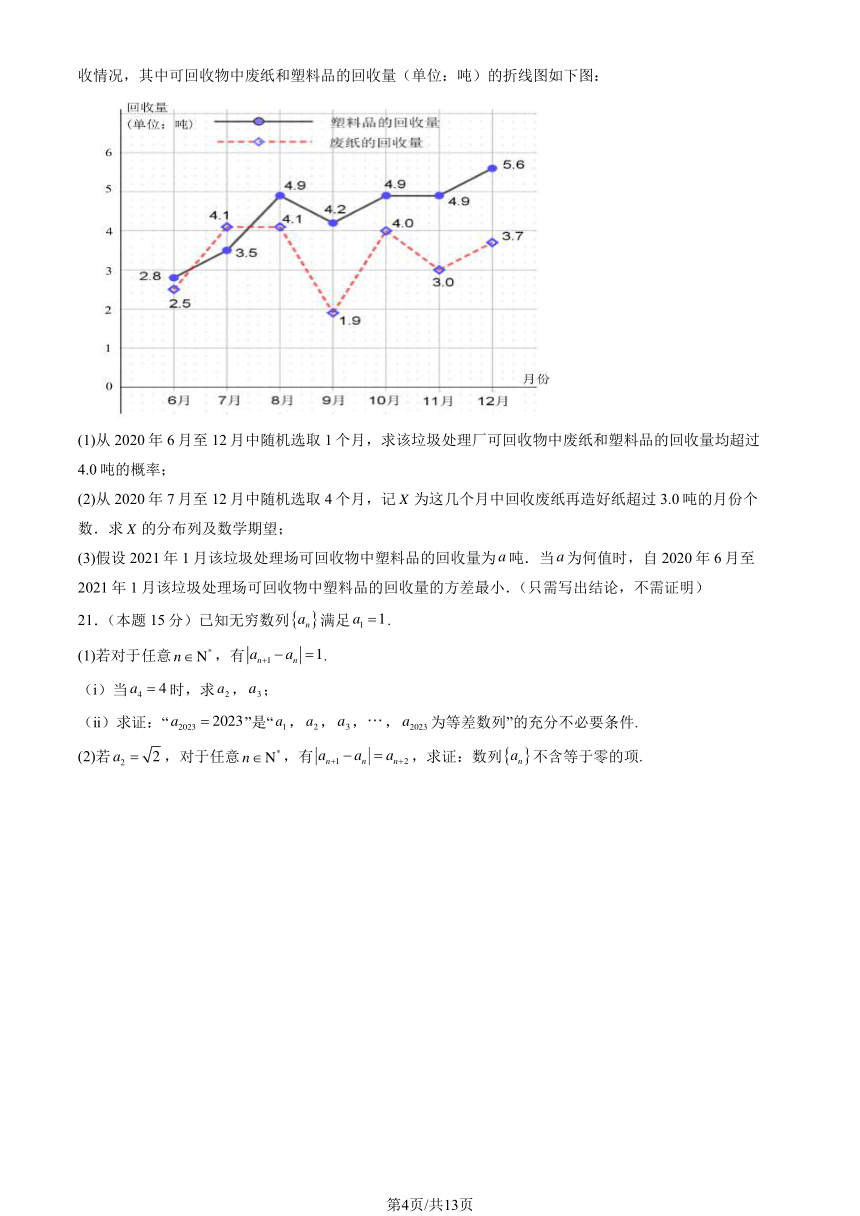
A.24
B.30
C.36
D.60
4
2.(本题4分)在数列a}中,若a=1,a2-,则a=()
A.-2
B
C.1
D.4
3.(本题4分)若(1-2x)5=a+ax+a2x2+…+ax,则a2+a4=()
A.100
B.110
C.120
D.130
4.(本题4分)已知数列{a}的前n项和为Sn=3”-1,则a=()
A.81
B.162
C.243
D.486
3
5.(本题4分)若
-
的展开式中各项系数之和为-128,则展开式中x2的系数为()
A.-2835
B.945
C.2835
D.-945
6.(本题4分)等比数列{an}满足a+a+a=7,a+a,+a=28,则a+a1+a3=()
A.56
B.56
C.-112
D.112
7.(本题4分)甲、乙、丙、丁四名同学参加学校组织的植树活动,学校共组织了3个植树小组,每人只能参
加一个植树小组,则甲、乙不在同一个植树小组的安排方法有()
A.81种
B.54种
C.36种
D.12种
8.(本题4分)在数字通信中,信号是由数字0和1组成的序列由于随机因素的干扰,发送的信号0或1
可能被错误的接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号为1时,
接收为1和0的概率分别为P和1-p.假设发送信号0和1是等可能的.已知接收到1的概率为0.475,则p
的值为()
A.0.8
B.0.85
C.0.9
D.0.95
9.(本题4分)排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得1分,得分的队有发球权,最
后先得25分的队获得本局比赛胜利,若出现比分24:24,要继续比赛至某队领先2分才能取胜,该局比赛
结束甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为子,乙队发球时甲队获胜的概率为
,且各次发球的胜负结果相互独立若此时甲、乙两队双方比分为2:22平,且甲队拥有发球权,则甲队
2
得25分且取得该局比赛胜利的概率为()
第1页/共13页
8
A.
72
64
27
B.
135
C.135
80
D.
135
10.(本题4分)己知Sn是数列{a}的前n项和,且a=a2=1,a=2a-1+3a-2(n≥3),则下列结论正
确的是()
A.数列{a-an}为等比数列
B.数列{a1+2an}为等比数列
Cs。e*-
D.=
1+(-1)1
2
二、填空题(共25分)
2n-1,n为奇数
11.(本题5分)在数列{an}中,若a=
21,n为偶数,则a+8的值为一
12.(本题5分)在等差数列{an}中,a=2,d=3,则{a}的前10项和So=
13.(本题5分)已知甲、乙两人投篮的命中率分别为0.5和0.8,且两人投篮相互没有影响.若投进一球得
2分,未进得0分,则每人投篮一次,得分相等的概率为
14.(本题5分)如图,在由二项式系数所构成的杨辉三角形中,第10行中最大的数与第二大的数的数值
之比为(用最简分数表示)
第0行
1
第1行
11
第2行
121
第3行
1331
第4行
14641
第5行15101051
中年非年年■g年g卡中卡中
15.(本题5分)己知数列{an}:112,12,4,12,4,8…,其中第一项是2°,接下来的两项是2°,2,再接下来
的三项是2°,2,22,…,以此类推,则下列说法正确的是一·
①第10个1出现在第46项:
②该数列的前55项的和是1012:
③存在连续六项之和是3的倍数:
④满足前n项之和为2的整数幂,且n>100的最小整数n的值为440
三、解答题(共85分)
16.(本题13分)已知在等差数列{a}中,a=3,a=-5.
(1)求数列{a}的通项公式:
(2)若数列{a}的前n项和S,则当n为何值时S,取得最大,并求出此最大值.
17.(本题13分)已知公差不为0的等差数列{a}的前n项和为S,且s4=20,a1,a2,a4成等比数列.
(1)求数列{a}的通项公式:
第2页/共13页
数
学
2024.4
(考试时间120分钟满分150分)
一、单选题(共40分)
1.(本题4分)从0,1,2,3,4中选出3个数组成各位数字不重复的3位偶数,这样的数有()个.
A.24
B.30
C.36
D.60
4
2.(本题4分)在数列a}中,若a=1,a2-,则a=()
A.-2
B
C.1
D.4
3.(本题4分)若(1-2x)5=a+ax+a2x2+…+ax,则a2+a4=()
A.100
B.110
C.120
D.130
4.(本题4分)已知数列{a}的前n项和为Sn=3”-1,则a=()
A.81
B.162
C.243
D.486
3
5.(本题4分)若
-
的展开式中各项系数之和为-128,则展开式中x2的系数为()
A.-2835
B.945
C.2835
D.-945
6.(本题4分)等比数列{an}满足a+a+a=7,a+a,+a=28,则a+a1+a3=()
A.56
B.56
C.-112
D.112
7.(本题4分)甲、乙、丙、丁四名同学参加学校组织的植树活动,学校共组织了3个植树小组,每人只能参
加一个植树小组,则甲、乙不在同一个植树小组的安排方法有()
A.81种
B.54种
C.36种
D.12种
8.(本题4分)在数字通信中,信号是由数字0和1组成的序列由于随机因素的干扰,发送的信号0或1
可能被错误的接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号为1时,
接收为1和0的概率分别为P和1-p.假设发送信号0和1是等可能的.已知接收到1的概率为0.475,则p
的值为()
A.0.8
B.0.85
C.0.9
D.0.95
9.(本题4分)排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得1分,得分的队有发球权,最
后先得25分的队获得本局比赛胜利,若出现比分24:24,要继续比赛至某队领先2分才能取胜,该局比赛
结束甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为子,乙队发球时甲队获胜的概率为
,且各次发球的胜负结果相互独立若此时甲、乙两队双方比分为2:22平,且甲队拥有发球权,则甲队
2
得25分且取得该局比赛胜利的概率为()
第1页/共13页
8
A.
72
64
27
B.
135
C.135
80
D.
135
10.(本题4分)己知Sn是数列{a}的前n项和,且a=a2=1,a=2a-1+3a-2(n≥3),则下列结论正
确的是()
A.数列{a-an}为等比数列
B.数列{a1+2an}为等比数列
Cs。e*-
D.=
1+(-1)1
2
二、填空题(共25分)
2n-1,n为奇数
11.(本题5分)在数列{an}中,若a=
21,n为偶数,则a+8的值为一
12.(本题5分)在等差数列{an}中,a=2,d=3,则{a}的前10项和So=
13.(本题5分)已知甲、乙两人投篮的命中率分别为0.5和0.8,且两人投篮相互没有影响.若投进一球得
2分,未进得0分,则每人投篮一次,得分相等的概率为
14.(本题5分)如图,在由二项式系数所构成的杨辉三角形中,第10行中最大的数与第二大的数的数值
之比为(用最简分数表示)
第0行
1
第1行
11
第2行
121
第3行
1331
第4行
14641
第5行15101051
中年非年年■g年g卡中卡中
15.(本题5分)己知数列{an}:112,12,4,12,4,8…,其中第一项是2°,接下来的两项是2°,2,再接下来
的三项是2°,2,22,…,以此类推,则下列说法正确的是一·
①第10个1出现在第46项:
②该数列的前55项的和是1012:
③存在连续六项之和是3的倍数:
④满足前n项之和为2的整数幂,且n>100的最小整数n的值为440
三、解答题(共85分)
16.(本题13分)已知在等差数列{a}中,a=3,a=-5.
(1)求数列{a}的通项公式:
(2)若数列{a}的前n项和S,则当n为何值时S,取得最大,并求出此最大值.
17.(本题13分)已知公差不为0的等差数列{a}的前n项和为S,且s4=20,a1,a2,a4成等比数列.
(1)求数列{a}的通项公式:
第2页/共13页
同课章节目录
