3.4 方差

3.4 方差
学习目标：
1．经历刻画数据离散程度的探索过程，感受表示数据离散程度的必要性.
2．知道极差、方差的意义，会计算一组数据的极差与方差．
学习重点：理解极差和方差概念，并在具体情境中加以应用．
学习难点：应用极差和方差概念解释实际问题中数据的离散程度，并形成相应的数学经验．
一、学前准备：
1.某日在不同时刻测得乌鲁木齐和广州的气温情况如下:
0:00
4:00
8:00
12:00
16:00
20:00
乌鲁木齐
10°c
14°c
20°c
24°c
19°c
16°c
广州
20°c
22°c
23°c
25°c
23°c
21°c
(1)乌鲁木齐和广州的气温的最大值、最小值各是多少？
(2)两地区某日的气温极差是多少？
2.质检部门从A、B两厂生产的乒乓球中各抽取了10只，对这些乒乓球的直径进行了检测，结果如下（单位：mm）21世纪教育网版权所有
A厂： 40.0， 39.9， 40.0， 40.1， 40.2， 39.8， 40.0， 39.9， 40.0， 40.1
B厂： 39.8， 40.2， 39.8， 40.2， 39.9， 40.1， 39.8， 40.2， 39.8， 40.2
思考探索：
（1）分别计算它们的平均数都是40 ，A厂数据的极差是 ，B厂数据的极差是 .
（2）将上面两组数据绘制成下图，你能发现哪组数据较稳定？
直径/mm 直径/mm



A厂 B厂
（3）怎样更精确的表示这两组数据的离散程度？
用一组数据x1，x2，…，xn与它们的平均数的差的平方的平均数，即
来描述这组数据的离散程度，并把它叫做这组数据的方差.
（4）请计算A、B两厂生产的乒乓球直径的方差.
二、探究活动
1.甲、乙两台机床生产同种零件，10天出的次品分别是：
甲：0、1、0、2、2、0、3、1、2、4
乙：2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差，根据你的计算判断哪台机床的性能较好？
三、学习体会
1．本节课你有哪些收获？ 2．预习时的疑难解决了吗？你还有哪些疑惑？
四、自我测试
1.数据 0 , -1 , 3 , 2 , 4 的极差是 .
2.甲、乙两支仪仗队的队员人数相同，平均身高相同，身高的方差分别为S2甲=0.9，S2乙=1.1，则甲、乙两支仪仗队的队员身高更整齐的是 . 21教育网
3.数据1，2，3，4，5的方差是 .
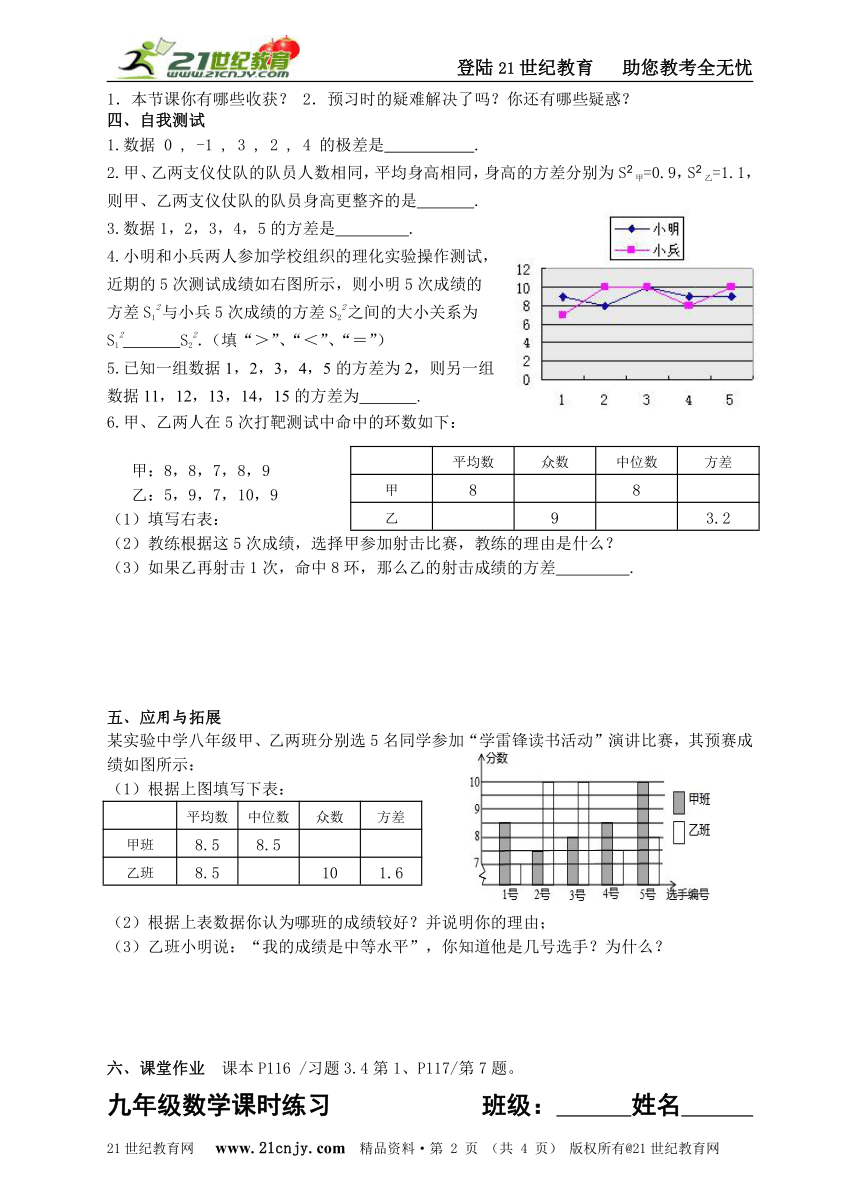
4.小明和小兵两人参加学校组织的理化实验操作测试，
近期的5次测试成绩如右图所示，则小明5次成绩的
方差S12与小兵5次成绩的方差S22之间的大小关系为
S12 S22．（填“＞”、“＜”、“＝”）
5.已知一组数据1，2，3，4，5的方差为2，则另一组
数据11，12，13，14，15的方差为 .
平均数
众数
中位数
方差
甲
8
?
8
乙
?
9
?
3.2
6.甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9乙：5，9，7，10，9
（1）填写右表：
（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差 .
五、应用与拓展
某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图所示：（1）根据上图填写下表：21cnjy.com
平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6
（2）根据上表数据你认为哪班的成绩较好？并说明你的理由；（3）乙班小明说：“我的成绩是中等水平”，你知道他是几号选手？为什么？
六、课堂作业 课本P116 /习题3.4第1、P117/第7题。
九年级数学课时练习 班级： 姓名
3.4 方差
1、（2015★湖南常德）某村引进甲乙两种水稻良种，各选6块条件相同的实验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为550kg/亩，方差分别为，，则产量稳定，适合推广的品种为：（ ）21·cn·jy·com
A、甲、乙均可； B、甲； C、乙； D、无法确定
2、（2011山东德州5,3分）某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：
对这两名运动员的成绩进行比较，下列四个结论中，不正确的是（ ）
（A）甲运动员得分的极差大于乙运动员得分的极差
（B）甲运动员得分的的中位数大于乙运动员得分的的中位数
（C）甲运动员的得分平均数大于乙运动员的得分平均数
（D）甲运动员的成绩比乙运动员的成绩稳定
3、（2011广东湛江9,3分）甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是环，方差分别是，， ，则射箭成绩最稳定的是（ ）A甲 B乙 C丙 D丁 www.21-cn-jy.com
4、市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩（单位：m）如下：2·1·c·n·j·y
甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的跳高平均成绩分别是多少？(2)哪位运动员的成绩更为稳定？
(3)若预测，跳过1.65m就很可能获得冠军，该校为了获得冠军，可能选哪位运动员参赛？若预测跳过1.70m才能得冠军呢？【来源：21·世纪·教育·网】
参考答案：
C；
D；
D；
4、本题是一道数据分析有关的实际问题,主要考查数据的平均数、方差的计算方法及处理数据的能力.根据平均数及方差的计算公式可得21·世纪*教育网
（1）==1.69(m),==1.68（m）.
(2)=0.0006(m2),
=0.0035(m2),因为,所以甲稳定.
（3）可能选甲参加，因为甲8次成绩都跳过1.65m而乙有3次低于1.65m;可能选乙参加，因为甲仅3次超过1.70m.