五年级上册数学人教版用字母表示数(课件)(共19张PPT)
文档属性
| 名称 | 五年级上册数学人教版用字母表示数(课件)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 326.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 10:22:51 | ||
图片预览




文档简介
(共19张PPT)
3.1.1 用字母表示数
我校课外制作小组同学准备制作一座房子模型,它的窗框如图所示,该窗是这样设计的:
上半部分为半圆,下半部分为六个大小一样的长方形,长方形的长与宽之比为3:2。
问题:至少需要多长的材料?
情 景
1、若每个长方形的长是30cm,你能够算出所需要的材料长是多少吗?试一试
2、如果每个长方形的长不知道是多少,我们可以用什么来表示?它所需要的材料是多少可以表示出来吗?试一试
答:至少需要材料(350+30∏)cm
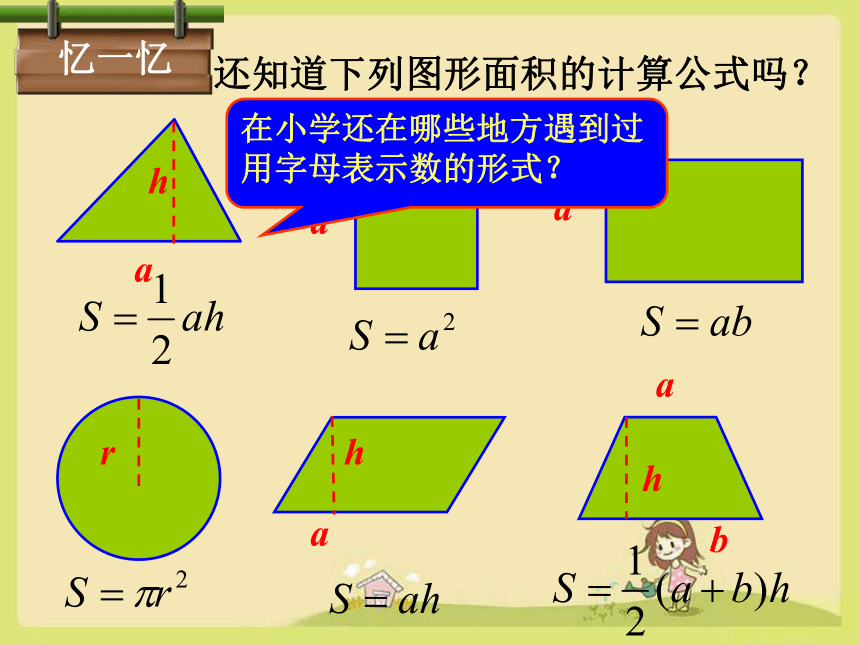
还知道下列图形面积的计算公式吗?
.
h
a
a
a
b
a
r
a
h
a
b
h
忆一忆
在小学还在哪些地方遇到过用字母表示数的形式?
75
50
40
25
20
弹起高度
150
100
80
50
40
下落高度
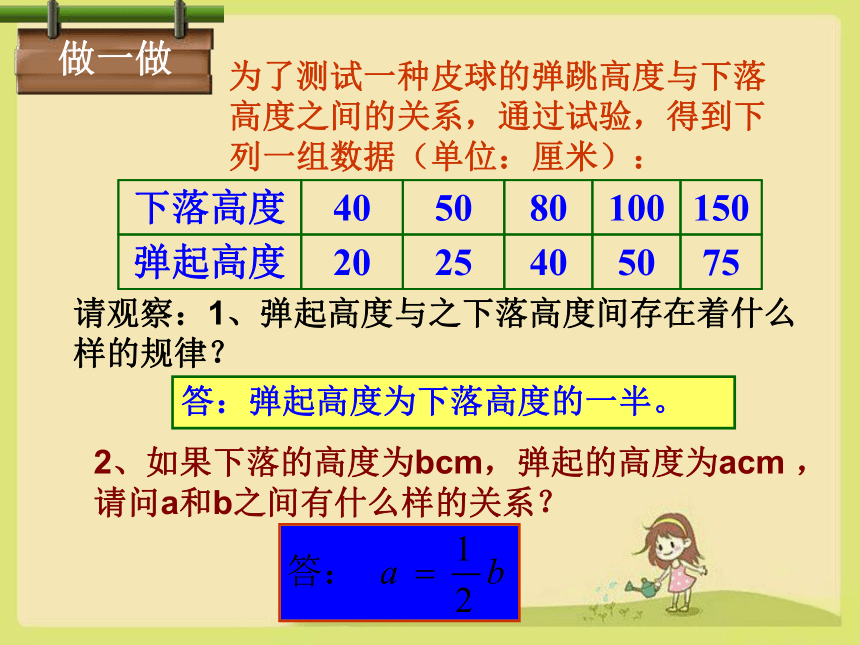
请观察:1、弹起高度与之下落高度间存在着什么样的规律?
2、如果下落的高度为bcm,弹起的高度为acm ,请问a和b之间有什么样的关系?
答:弹起高度为下落高度的一半。
做一做
为了测试一种皮球的弹跳高度与下落高度之间的关系,通过试验,得到下列一组数据(单位:厘米):
请发现下面式子的规律,并用n表示出来
1、 12+1=1×2
2、 22+2=2×3
3、 32+3=3×4
……………
n 、
n2+n=n×(n+1)
做一做
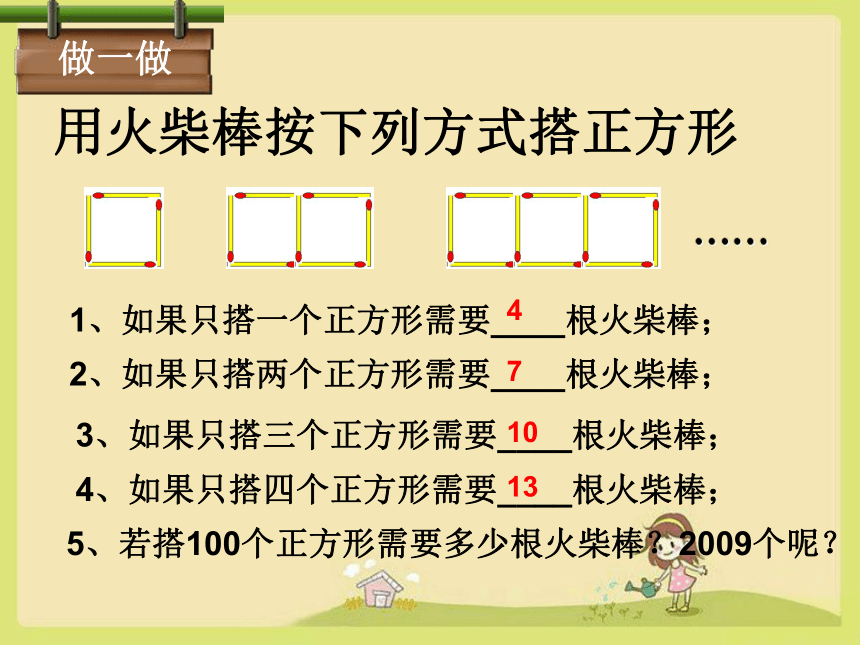
用火柴棒按下列方式搭正方形
1、如果只搭一个正方形需要____根火柴棒;
2、如果只搭两个正方形需要____根火柴棒;
3、如果只搭三个正方形需要____根火柴棒;
4、如果只搭四个正方形需要____根火柴棒;
5、若搭100个正方形需要多少根火柴棒?2009个呢?
……
4
7
10
13
如果要搭n个这样的正方形,需要多少根这样的火柴棒?你是怎样思考的?
……
n个
4+3(n-1)=3n+1
(n-1)个
……
……
n个
1+3n
n个
……
……
n个
n+n+(n+1)=3n+1
n根
n根
……
……
……
……
n个
4n-(n-1) =3n+1
n个
(n-1)根
……
……
n个
a
a
1
b
2
b
3
长方形③的面积为 ;
于是整个图形的面积为 ;
又因为大正方形的面积为 ;
所以可以得到等式: .
a2
b2
4
如图:正方形①的面积为 ;
正方形④的面积为 ;
长方形②的面积为 ;
ab
ab
a2+ab+ab+b2
(a+b)2
=a2+ab+ab+b2
(a+b)2
填空:
(1)某地为了治理河山,改造环境,计划在第十个
五年计划期间植树绿化荒山,如果每年植树绿化x公
顷荒山,那么这五年内植树绿化荒山 公顷;
(3)每本练习本m元,每支钢笔n元,甲买了5本练习本,乙买了2支钢笔,两人一共花了 元,甲比乙多花了 元.
(5m+2n)
(5m-2n)
(2) 如果小红用t小时走完的路程为s千米,那么她走这段路程的平均速度为______千米/时;
s
t
5x
在填空题中,如果填入的式子是多项的,就要把整个式子加上“括号”
做一做
1.填空:
(1) 一打铅笔有12枝,n打铅笔有 枝;
(2) 三角形的三边长分别为3a 、4a 、5a,则其周
长为 ;
(3) 如图,某广场四角铺上了四分之一圆形的草地,
平方米.
若圆形的半径为r米,则共有草地
12n
(3a+4a+5a)
r
2
π
练一练
×
10
×
10
2
+
+
c
a
b
2. 我们知道:
23=
×
2
10+3
865=
×
10
2
8
×
10+5
+6
;
;
×
10
2
×
10
5984=
×
10
3
+
+
+
.
类似地,
若某三位数的个位数字为a,十位数字为b,百位数
.
字为c,则此三位数可表示为
5
9
8
4
若某三位数十位数字为a,个位数字是十位数字的2倍,百位数字比十位数字大1,则这个三位数可以表示为什么?
(a+1) ×102+a ×10+2a
2、用字母表示数可以反映出一些普遍带有规律性的问题,揭示出由特殊到一般的认知过程;
用字母表示数,可以把运算律、图形的面积、周长、体积等数量关系和一些式子或图形的规律简明地表示出来,形式简单,使用方便。
1、学了本节课,你对“字母表示数”有什么感受
学习反思
作业
P92页 习题3.1 1, 2,3题
谢谢各位老师,
谢谢同学们!
3.1.1 用字母表示数
我校课外制作小组同学准备制作一座房子模型,它的窗框如图所示,该窗是这样设计的:
上半部分为半圆,下半部分为六个大小一样的长方形,长方形的长与宽之比为3:2。
问题:至少需要多长的材料?
情 景
1、若每个长方形的长是30cm,你能够算出所需要的材料长是多少吗?试一试
2、如果每个长方形的长不知道是多少,我们可以用什么来表示?它所需要的材料是多少可以表示出来吗?试一试
答:至少需要材料(350+30∏)cm
还知道下列图形面积的计算公式吗?
.
h
a
a
a
b
a
r
a
h
a
b
h
忆一忆
在小学还在哪些地方遇到过用字母表示数的形式?
75
50
40
25
20
弹起高度
150
100
80
50
40
下落高度
请观察:1、弹起高度与之下落高度间存在着什么样的规律?
2、如果下落的高度为bcm,弹起的高度为acm ,请问a和b之间有什么样的关系?
答:弹起高度为下落高度的一半。
做一做
为了测试一种皮球的弹跳高度与下落高度之间的关系,通过试验,得到下列一组数据(单位:厘米):
请发现下面式子的规律,并用n表示出来
1、 12+1=1×2
2、 22+2=2×3
3、 32+3=3×4
……………
n 、
n2+n=n×(n+1)
做一做
用火柴棒按下列方式搭正方形
1、如果只搭一个正方形需要____根火柴棒;
2、如果只搭两个正方形需要____根火柴棒;
3、如果只搭三个正方形需要____根火柴棒;
4、如果只搭四个正方形需要____根火柴棒;
5、若搭100个正方形需要多少根火柴棒?2009个呢?
……
4
7
10
13
如果要搭n个这样的正方形,需要多少根这样的火柴棒?你是怎样思考的?
……
n个
4+3(n-1)=3n+1
(n-1)个
……
……
n个
1+3n
n个
……
……
n个
n+n+(n+1)=3n+1
n根
n根
……
……
……
……
n个
4n-(n-1) =3n+1
n个
(n-1)根
……
……
n个
a
a
1
b
2
b
3
长方形③的面积为 ;
于是整个图形的面积为 ;
又因为大正方形的面积为 ;
所以可以得到等式: .
a2
b2
4
如图:正方形①的面积为 ;
正方形④的面积为 ;
长方形②的面积为 ;
ab
ab
a2+ab+ab+b2
(a+b)2
=a2+ab+ab+b2
(a+b)2
填空:
(1)某地为了治理河山,改造环境,计划在第十个
五年计划期间植树绿化荒山,如果每年植树绿化x公
顷荒山,那么这五年内植树绿化荒山 公顷;
(3)每本练习本m元,每支钢笔n元,甲买了5本练习本,乙买了2支钢笔,两人一共花了 元,甲比乙多花了 元.
(5m+2n)
(5m-2n)
(2) 如果小红用t小时走完的路程为s千米,那么她走这段路程的平均速度为______千米/时;
s
t
5x
在填空题中,如果填入的式子是多项的,就要把整个式子加上“括号”
做一做
1.填空:
(1) 一打铅笔有12枝,n打铅笔有 枝;
(2) 三角形的三边长分别为3a 、4a 、5a,则其周
长为 ;
(3) 如图,某广场四角铺上了四分之一圆形的草地,
平方米.
若圆形的半径为r米,则共有草地
12n
(3a+4a+5a)
r
2
π
练一练
×
10
×
10
2
+
+
c
a
b
2. 我们知道:
23=
×
2
10+3
865=
×
10
2
8
×
10+5
+6
;
;
×
10
2
×
10
5984=
×
10
3
+
+
+
.
类似地,
若某三位数的个位数字为a,十位数字为b,百位数
.
字为c,则此三位数可表示为
5
9
8
4
若某三位数十位数字为a,个位数字是十位数字的2倍,百位数字比十位数字大1,则这个三位数可以表示为什么?
(a+1) ×102+a ×10+2a
2、用字母表示数可以反映出一些普遍带有规律性的问题,揭示出由特殊到一般的认知过程;
用字母表示数,可以把运算律、图形的面积、周长、体积等数量关系和一些式子或图形的规律简明地表示出来,形式简单,使用方便。
1、学了本节课,你对“字母表示数”有什么感受
学习反思
作业
P92页 习题3.1 1, 2,3题
谢谢各位老师,
谢谢同学们!
