20.2数据的集中趋势与离散程度(5)
文档属性
| 名称 | 20.2数据的集中趋势与离散程度(5) |

|
|
| 格式 | pptx | ||
| 文件大小 | 146.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
20.2数据的集中趋势与离散程度(5)
方差
教学目标:
1.经历方差的形成过程,了解方差的意义;
2.掌握方差的计算方法并会初步运用方差解决
实际问题.
教学重点:
掌握方差的计算方法并会初步运用方差解决
实际问题.
教学难点:
运用方差对数据波动情况的比较、判断.
机床A
20.0
19.8
20.1
20.2
19.9
20.0
20.2
19.8
20.2
19.8
机床B
20.0
20.0
19.9
20.0
19.9
20.2
20.0
20.1
20.1
19.8
根据这些数据估计,判断哪台机床生产的零件的精度更稳定.
两台机床都生产直径为(20±2)mm的零件,为了检验产品质量,从中各抽出10个进行测量,结果如下(单位:mm) :
情景导入 生成问题
两台机床生产的零件直径的平均值怎样?
20.0+19.8+…+19.8
10
=20.0
XB
=
20.0+20.0+…+19.8
10
=20.0
机床A
20.0
19.8
20.1
20.2
19.9
20.0
20.2
19.8
20.2
19.8
机床B
20.0
20.0
19.9
20.0
19.9
20.2
20.0
20.1
20.1
19.8
要比较,首先想到比较两组数据的平均值:
XA
=
XA
=
XB
=20.0mm,
它们的中位数也都是20.0mm,
从数据集中趋势这个角度很难区分两台机床生产的
零件的精度的稳定性.
这就需考察数据的离散程度.
10
2
4
6
8
0
19.8
20.2
19.9
零件直径/mm
20.1
20.0
10
2
4
6
8
0
19.8
20.2
19.9
零件直径/mm
20.1
20.0
机床A
机床B
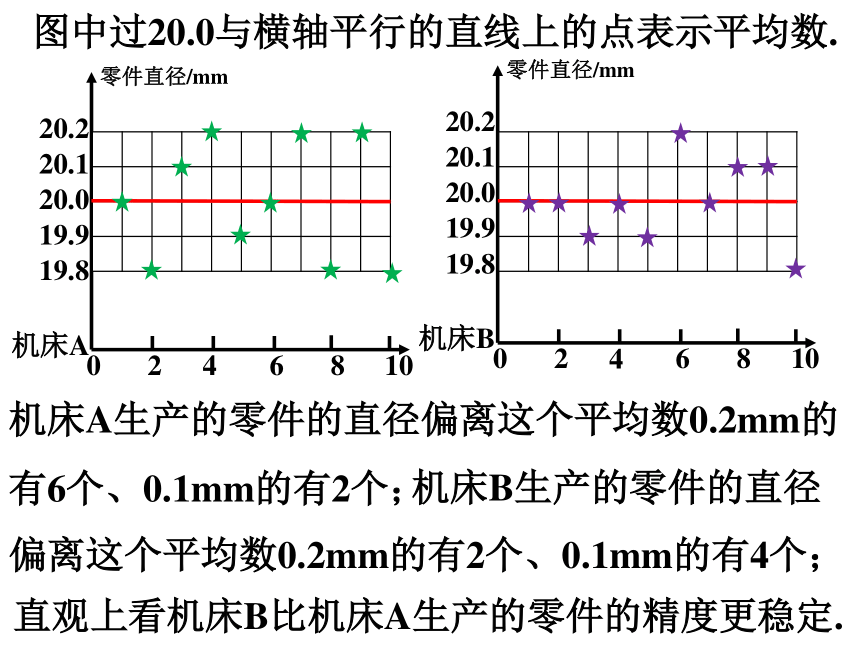
图中过20.0与横轴平行的直线上的点表示平均数.
机床A生产的零件的直径偏离这个平均数0.2mm的
有6个、0.1mm的有2个;
机床B生产的零件的直径
偏离这个平均数0.2mm的有2个、0.1mm的有4个;
直观上看机床B比机床A生产的零件的精度更稳定.
阅读教材 P128~130,完成下列问题:
什么是方差 方差的作用是什么
统计学中常采用下面的做法来刻画这组数据的离散程度:
设有n个数据x1,x2,…,xn,
各数据与它们的
S2=
1
n
[(x1-x)2+(x2-x)2+…+(xn-x)2]
(x1-x)2
, , , .
(x2-x)2
(xn-x)2
…
平均数 的差的平方分别是:
X
来衡量这组数据的离散程度,称它为这组数据的方差.
我们用这些值的平均数,即用
方差及其计算公式与意义
方差越大,数据的波动越大;
方差越小,数据的波动越小.
S2=
1
n
[(x1-x)2+(x2-x)2+…+(xn-x)2]
方差计算公式
方差的作用
衡量一组数据的离散程度.
形成新知
方差的计算步骤:
S2=
1
n
1.计算样本数据的平均数,
2.计算各个数据与平均数的差的平方,
3.计算各个数据与平均数的差的平方的平均数.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
方差及其计算
解:
∵
∴
S2A
=
(20.0-20)2+(19.8-20)2+…+(19.8-20)2
10
=0.026
<S2A,
(20.0-20)2+(20.0-20)2+…+(19.8-20)2
10
=0.012
∵S2B
S2B
=
∴机床A和机床B生产的零件的精度更稳定.
下面通过计算方差,来评判机床A和机床B
哪台生产的零件的精度更稳定.
20.0+19.8+…+19.8
10
=20
XB
=
20.0+20.0+…+19.8
10
=20
XA
=
1.计算下列各组数据的方差:
(1)A: 11 12 13 14 15 ; B: 11 13 13 14;
(2)A: 30 50 50 50 60; B: 30 44 50 56 60.
S2A
=
(11-13)2+(12-13)2+…+(15-13)2
5
=2
S2B
=
(11-12.75)2+(13-12.75)2+…+(14-12.75)2
4
≈1.19
S2A
=
(30-48)2+(50-48)2+…+(60-48)2
5
=96
S2B
=
(30-48)2+(44-48)2+…+(60-48)2
5
≈110.4
(1)
(2)
练习巩固
2.考察甲、乙两种小麦的长势,分别从中抽取
10株苗,测得苗高如下(单位:mm)
甲: 12 13 14 15 10 16 13 11 15 11;
乙: 11 16 17 14 13 19 6 8 10 16.
S2甲
=
(12-13)2+(13-13)2+…+(11-13)2
10
=3.6
S2乙
=
(11-13)2+(16-13)2+…+(16-13)2
10
=15.8
解:
计算甲、乙两组数据的方差,
说明哪种小麦长得较整齐.
<S2乙,
∵S2甲
∴甲种小麦长得较整齐.
1.方差是刻画数据波动程度的量.对于一组
数据x1,x2,…,xn,可用如下公式计算方差
练习巩固
S2=
1
n
[(x1-5)2+(x2-5)2+(x3-5)2 +…+(xn-5)2]
其中的“5”是这组数据的( ).
A.最小值 B.平均数
C.中位数 D.众数
B
2.甲、乙两位同学比赛射击,两人所得平均环数相同,其中甲所得环数的方差为9,乙所得环数的方差为6,那么成绩较为稳定的是 (填“甲”或“乙”).
乙
练习巩固
练习巩固
4.一组数据:4,3,5,8,5 的方差是 .
3.数据组:6,6,6,6,6,6的方差是 .
0
2.8
5.甲、乙、丙三个旅行团的游客人数都相等且每个团游客的平均年龄都是35岁,这三个团游客年龄的方差分别是 S2甲=1.4,S2乙=18.8,S2丙 =25,导游小方最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( ).
A.甲队 B.乙队
C.丙队 D.任一队都可以
A
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用
方差来判断它们的波动情况.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
S2=
1
n
课堂小结
B
3.一组数据:3,4,5,x,8 的众数是5,则这组数据的方差是( ).
A.2 B.2.4 C.2.8 D.3
A.众数是108, B.中位数是105,
C.平均数是101, D.方差是93.
4.某校九年级模拟考试中,1班的六名学生
的数学成绩如下:96,108,102,110,108,82.
下列关于这组数据的描述不正确的是( ).
D
C
5.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法中不正确的是( ).
A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙的众数相同
D
今天作业
课本P136页第9、10题
20.2数据的集中趋势与离散程度(5)
方差
教学目标:
1.经历方差的形成过程,了解方差的意义;
2.掌握方差的计算方法并会初步运用方差解决
实际问题.
教学重点:
掌握方差的计算方法并会初步运用方差解决
实际问题.
教学难点:
运用方差对数据波动情况的比较、判断.
机床A
20.0
19.8
20.1
20.2
19.9
20.0
20.2
19.8
20.2
19.8
机床B
20.0
20.0
19.9
20.0
19.9
20.2
20.0
20.1
20.1
19.8
根据这些数据估计,判断哪台机床生产的零件的精度更稳定.
两台机床都生产直径为(20±2)mm的零件,为了检验产品质量,从中各抽出10个进行测量,结果如下(单位:mm) :
情景导入 生成问题
两台机床生产的零件直径的平均值怎样?
20.0+19.8+…+19.8
10
=20.0
XB
=
20.0+20.0+…+19.8
10
=20.0
机床A
20.0
19.8
20.1
20.2
19.9
20.0
20.2
19.8
20.2
19.8
机床B
20.0
20.0
19.9
20.0
19.9
20.2
20.0
20.1
20.1
19.8
要比较,首先想到比较两组数据的平均值:
XA
=
XA
=
XB
=20.0mm,
它们的中位数也都是20.0mm,
从数据集中趋势这个角度很难区分两台机床生产的
零件的精度的稳定性.
这就需考察数据的离散程度.
10
2
4
6
8
0
19.8
20.2
19.9
零件直径/mm
20.1
20.0
10
2
4
6
8
0
19.8
20.2
19.9
零件直径/mm
20.1
20.0
机床A
机床B
图中过20.0与横轴平行的直线上的点表示平均数.
机床A生产的零件的直径偏离这个平均数0.2mm的
有6个、0.1mm的有2个;
机床B生产的零件的直径
偏离这个平均数0.2mm的有2个、0.1mm的有4个;
直观上看机床B比机床A生产的零件的精度更稳定.
阅读教材 P128~130,完成下列问题:
什么是方差 方差的作用是什么
统计学中常采用下面的做法来刻画这组数据的离散程度:
设有n个数据x1,x2,…,xn,
各数据与它们的
S2=
1
n
[(x1-x)2+(x2-x)2+…+(xn-x)2]
(x1-x)2
, , , .
(x2-x)2
(xn-x)2
…
平均数 的差的平方分别是:
X
来衡量这组数据的离散程度,称它为这组数据的方差.
我们用这些值的平均数,即用
方差及其计算公式与意义
方差越大,数据的波动越大;
方差越小,数据的波动越小.
S2=
1
n
[(x1-x)2+(x2-x)2+…+(xn-x)2]
方差计算公式
方差的作用
衡量一组数据的离散程度.
形成新知
方差的计算步骤:
S2=
1
n
1.计算样本数据的平均数,
2.计算各个数据与平均数的差的平方,
3.计算各个数据与平均数的差的平方的平均数.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
方差及其计算
解:
∵
∴
S2A
=
(20.0-20)2+(19.8-20)2+…+(19.8-20)2
10
=0.026
<S2A,
(20.0-20)2+(20.0-20)2+…+(19.8-20)2
10
=0.012
∵S2B
S2B
=
∴机床A和机床B生产的零件的精度更稳定.
下面通过计算方差,来评判机床A和机床B
哪台生产的零件的精度更稳定.
20.0+19.8+…+19.8
10
=20
XB
=
20.0+20.0+…+19.8
10
=20
XA
=
1.计算下列各组数据的方差:
(1)A: 11 12 13 14 15 ; B: 11 13 13 14;
(2)A: 30 50 50 50 60; B: 30 44 50 56 60.
S2A
=
(11-13)2+(12-13)2+…+(15-13)2
5
=2
S2B
=
(11-12.75)2+(13-12.75)2+…+(14-12.75)2
4
≈1.19
S2A
=
(30-48)2+(50-48)2+…+(60-48)2
5
=96
S2B
=
(30-48)2+(44-48)2+…+(60-48)2
5
≈110.4
(1)
(2)
练习巩固
2.考察甲、乙两种小麦的长势,分别从中抽取
10株苗,测得苗高如下(单位:mm)
甲: 12 13 14 15 10 16 13 11 15 11;
乙: 11 16 17 14 13 19 6 8 10 16.
S2甲
=
(12-13)2+(13-13)2+…+(11-13)2
10
=3.6
S2乙
=
(11-13)2+(16-13)2+…+(16-13)2
10
=15.8
解:
计算甲、乙两组数据的方差,
说明哪种小麦长得较整齐.
<S2乙,
∵S2甲
∴甲种小麦长得较整齐.
1.方差是刻画数据波动程度的量.对于一组
数据x1,x2,…,xn,可用如下公式计算方差
练习巩固
S2=
1
n
[(x1-5)2+(x2-5)2+(x3-5)2 +…+(xn-5)2]
其中的“5”是这组数据的( ).
A.最小值 B.平均数
C.中位数 D.众数
B
2.甲、乙两位同学比赛射击,两人所得平均环数相同,其中甲所得环数的方差为9,乙所得环数的方差为6,那么成绩较为稳定的是 (填“甲”或“乙”).
乙
练习巩固
练习巩固
4.一组数据:4,3,5,8,5 的方差是 .
3.数据组:6,6,6,6,6,6的方差是 .
0
2.8
5.甲、乙、丙三个旅行团的游客人数都相等且每个团游客的平均年龄都是35岁,这三个团游客年龄的方差分别是 S2甲=1.4,S2乙=18.8,S2丙 =25,导游小方最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( ).
A.甲队 B.乙队
C.丙队 D.任一队都可以
A
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用
方差来判断它们的波动情况.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
S2=
1
n
课堂小结
B
3.一组数据:3,4,5,x,8 的众数是5,则这组数据的方差是( ).
A.2 B.2.4 C.2.8 D.3
A.众数是108, B.中位数是105,
C.平均数是101, D.方差是93.
4.某校九年级模拟考试中,1班的六名学生
的数学成绩如下:96,108,102,110,108,82.
下列关于这组数据的描述不正确的是( ).
D
C
5.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法中不正确的是( ).
A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙的众数相同
D
今天作业
课本P136页第9、10题
