2024年中考科学重点专题复习--浮力计算题(含解析)
文档属性
| 名称 | 2024年中考科学重点专题复习--浮力计算题(含解析) | 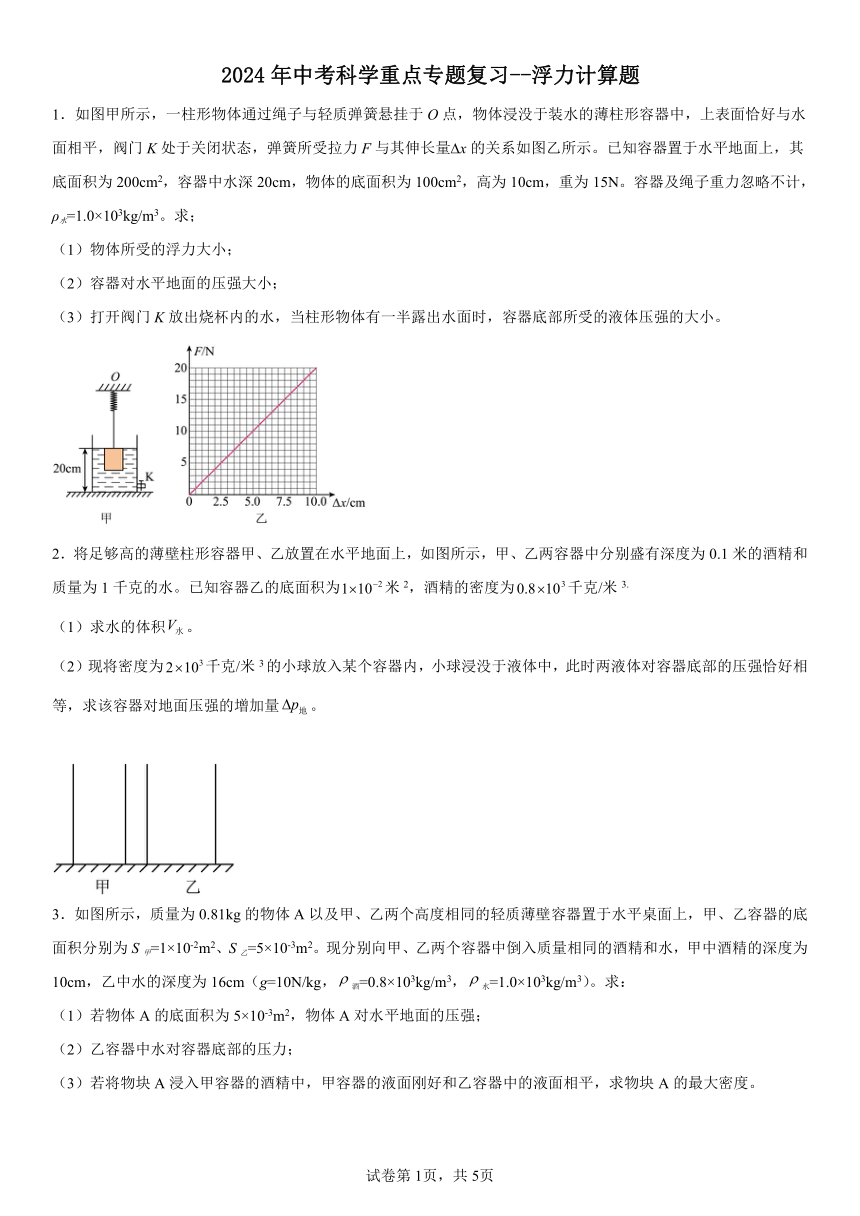 | |
| 格式 | docx | ||
| 文件大小 | 662.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2024-04-30 17:58:12 | ||
图片预览




文档简介
2024年中考科学重点专题复习--浮力计算题
1.如图甲所示,一柱形物体通过绳子与轻质弹簧悬挂于O点,物体浸没于装水的薄柱形容器中,上表面恰好与水面相平,阀门K处于关闭状态,弹簧所受拉力F与其伸长量 x的关系如图乙所示。已知容器置于水平地面上,其底面积为200cm2,容器中水深20cm,物体的底面积为100cm2,高为10cm,重为15N。容器及绳子重力忽略不计,ρ水=1.0×103kg/m3。求;
(1)物体所受的浮力大小;
(2)容器对水平地面的压强大小;
(3)打开阀门K放出烧杯内的水,当柱形物体有一半露出水面时,容器底部所受的液体压强的大小。
2.将足够高的薄壁柱形容器甲、乙放置在水平地面上,如图所示,甲、乙两容器中分别盛有深度为0.1米的酒精和质量为1千克的水。已知容器乙的底面积为米2,酒精的密度为千克/米3.
(1)求水的体积。
(2)现将密度为千克/米3的小球放入某个容器内,小球浸没于液体中,此时两液体对容器底部的压强恰好相等,求该容器对地面压强的增加量。
3.如图所示,质量为0.81kg的物体A以及甲、乙两个高度相同的轻质薄壁容器置于水平桌面上,甲、乙容器的底面积分别为S甲=1×10-2m2、S乙=5×10-3m2。现分别向甲、乙两个容器中倒入质量相同的酒精和水,甲中酒精的深度为10cm,乙中水的深度为16cm(g=10N/kg,酒=0.8×103kg/m3,水=1.0×103kg/m3)。求:
(1)若物体A的底面积为5×10-3m2,物体A对水平地面的压强;
(2)乙容器中水对容器底部的压力;
(3)若将物块A浸入甲容器的酒精中,甲容器的液面刚好和乙容器中的液面相平,求物块A的最大密度。
4.如图所示,正方体的边长为,在它的上面放一个重为2N的物体,此时正方体恰好没入水中,已知。求:(g取10 N/kg)
(1)正方体B受到的浮力的大小;
(2)正方体B的密度。
5.如图甲所示,一轻质弹簧,其两端分别固定在容器底部和正方体物块上。已知物块的边长为10cm,弹簧没有发生形变时的长度为16cm,弹簧受到拉力作用后,伸长的长度ΔL与拉力F的关系如图乙所示。向容器中加水,直到物块上表面与水面相平,此时水深30cm。求:(ρ水=1.0×103kg/m3,g取10N/kg)
(1)水对容器底部的压强;
(2)物块受到水的浮力;
(3)物块的密度。
6.一底面积为80cm 的容器放置在水平地面上(如图甲所示),内放有一柱形物体。物体是由高20cm、底部嵌有金属块的塑料制成。缓慢向图甲所示容器中注水到一定深度时物体会漂浮,继续注水到24cm时停止,注水质量m与容器中水的深度h的关系图像如图乙所示。当把物体水平切掉一部分后,剩余部分放入水中恰好悬浮(如图丙所示),测得物体剩余部分的质量为0.5kg。(、)求:
(1)剩余部分悬浮于水中时受到的浮力;
(2)注水停止时水对容器底部的压力;
(3)物体水平切掉的高度Δh和图乙中m2的值。
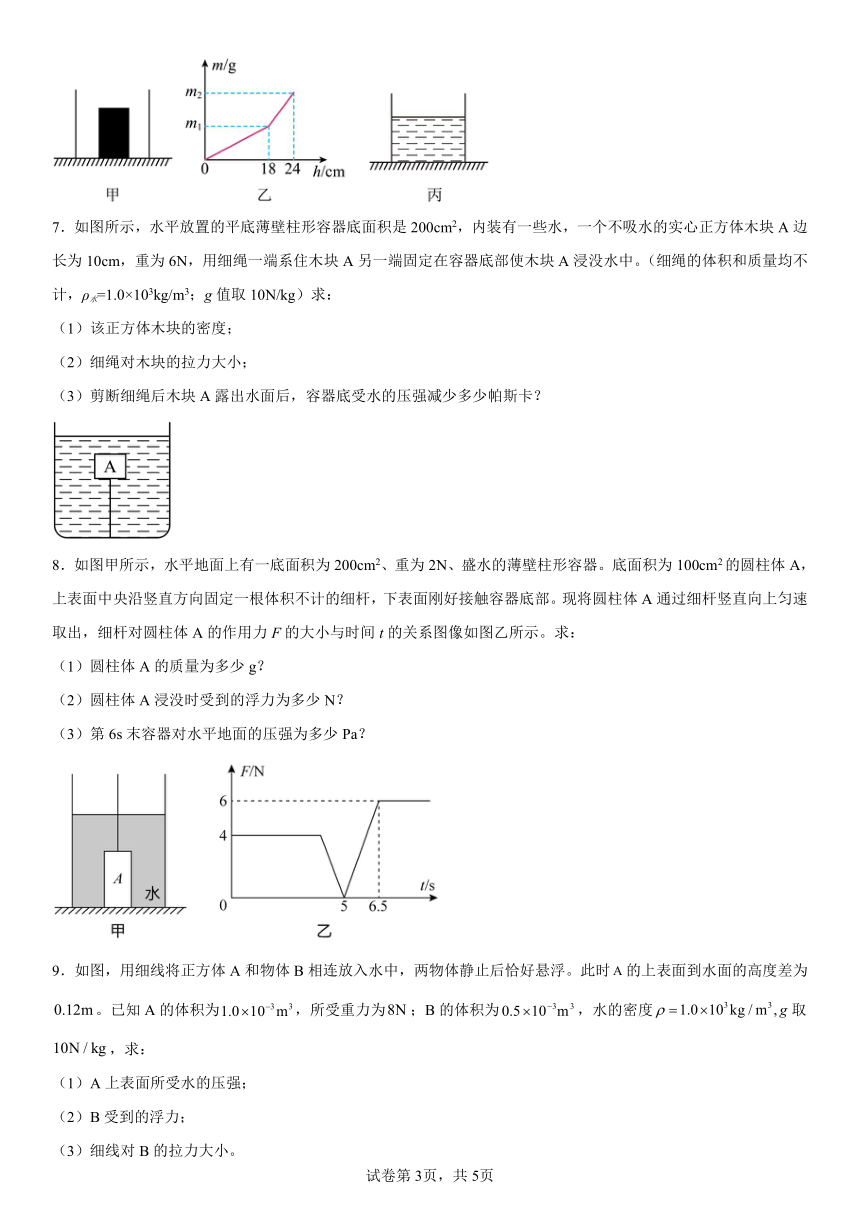
7.如图所示,水平放置的平底薄壁柱形容器底面积是200cm2,内装有一些水,一个不吸水的实心正方体木块A边长为10cm,重为6N,用细绳一端系住木块A另一端固定在容器底部使木块A浸没水中。(细绳的体积和质量均不计,ρ水=1.0×103kg/m3;g值取10N/kg)求:
(1)该正方体木块的密度;
(2)细绳对木块的拉力大小;
(3)剪断细绳后木块A露出水面后,容器底受水的压强减少多少帕斯卡?
8.如图甲所示,水平地面上有一底面积为200cm2、重为2N、盛水的薄壁柱形容器。底面积为100cm2的圆柱体A,上表面中央沿竖直方向固定一根体积不计的细杆,下表面刚好接触容器底部。现将圆柱体A通过细杆竖直向上匀速取出,细杆对圆柱体A的作用力F的大小与时间t的关系图像如图乙所示。求:
(1)圆柱体A的质量为多少g?
(2)圆柱体A浸没时受到的浮力为多少N?
(3)第6s末容器对水平地面的压强为多少Pa?
9.如图,用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮。此时的上表面到水面的高度差为。已知A的体积为,所受重力为;B的体积为,水的密度取,求:
(1)A上表面所受水的压强;
(2)B受到的浮力;
(3)细线对B的拉力大小。
10.如图甲所示,足够高质量为8kg的长方体容器C置于水平地面,不吸水的AB两物体叠放置于容器内,A为正方体,B为长方体,其中A的边长为10cm,B的高为0.1m,缓慢向容器中加水,直到容器中水的深度为0.12m时停止加水,所加水的质量与容器中水的深度关系如图乙所示,已知ρ水=1.0×103kg/cm3,g=10N/kg,求:
(1)停止加水时,水对容器底部的压强;
(2)物体A和B的总质量为多少kg;
(3)停止加水后,将物体A拿开,物体B相对于水面上升1cm,接着继续向容器中继续注水,当水对容器底部的压强与容器对桌面的压强之比为1:2时,再将A物体放入水中,此时水对容器底部的压力为多少N。(设物体上、下表面始终与水面平行)
11.有一体积、质量忽略不计的弹簧,其原长为10cm,把弹簧下端固定在容器底部,容器底面积200cm2,上端固定在边长为10cm的正方体木块上,向容器中加水直到木块上表面与液面相平,如图甲所示,此时水深为24cm。弹簧受到拉力作用时,弹簧伸长的长度ΔL与所受拉力F的关系如图乙所示。(ρ水=1.0×103kg/m3)求:
(1)水深为24cm时容器底部受到水的压强;
(2)木块受到水的浮力;
(3)木块的密度;
(4)打开出水孔,缓慢放水,当弹簧处于没有发生形变的自然状态时,关闭出水孔,此时放出水的质量。
12.某水底打捞作业中,需将一长方体石柱从水底匀速打捞出水,如图所示是吊车钢丝绳拉力F随石柱下表面距水底深度h变化的图像,水的阻力和液面变化忽略不计,求:
(1)长方体石柱浸没时在水中所受的浮力;
(2)长方体石柱的底面积;
(3)长方体石柱的密度。
13.如图甲所示,在水平桌面上放有一薄壁柱形容器,一个重力为5N,底面积为0.02m2,高为10cm的柱形玻璃杯A漂浮于水面,在A的底部连接有一个体积为4×10-5m3的实心金属块B。此时A、B两物体在水中处于静止状态,细线未拉直(B未与容器底部紧密接触,细线不可伸长且质量、体积忽略不计)。向容器中注水,细线拉力随时间变化的图象如图乙所示(容器足够高)。(水密度为1.0×103kg/m3,g取10N/kg)求:
(1)图甲中玻璃杯A所受浮力的大小;
(2)图甲中水对玻璃杯A底部的压强大小;
(3)实心金属块B的密度。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)10N;(2);(3)
【详解】解:(1)物体的体积为
物体浸没在水中所受的浮力大小为
(2)容器中水的体积为
水的重力为
物体间作用力是相互的,容器对桌面的压力为
容器对水平地面的压强为
(3)当柱形物体有一半露出水面时,减小的浮力为
根据,弹簧测力计的示数增大5N,如图所示,弹簧长度增大2.5cm,即物体下降2.5cm,此时的液面深度为
容器底部所受的液体压强为
答:(1)物体所受的浮力为10N;
(2)容器对水平地面的压强为;
(3)打开阀门K放出烧杯内的水,当柱形物体有一半露出水面时,容器底部所受的液体压强为。
2.(1)1×10-3m3;(2)500Pa
【详解】解:(1)水的体积
(2)酒精对容器底的压强
水对容器底的压强
由于p甲该容器对地面压强的增加量
答:(1)水的体积为1×10-3m3;
(2)该容器对地面压强的增加量为500Pa。
3.(1)1.62×103pa;(2)8N;(3)1.35×103kg/m3
【详解】解(1)在平面上物体的压力大小等于重力大小,所以压力为
则物体A对水平地面的压强
(2)乙容器中水对容器底部的压强为
则乙容器中水对容器底部的压力为
(3)浸入甲容器的物块,当物体浸没时物块的体积最小,则其密度最大,由于甲容器的液体进入物块后,甲容器的液面刚好和乙容器中的液面相平,则此时甲容器的液体深度为
物块的最小体积
所以物块A的最大密度为
答:(1)物体A对水平地面的压强为1.62×103pa;
(2)乙容器中水对容器底部的压力为8N;
(3)物块A的最大密度为1.35×103kg/m3。
4.(1)10N;(2)
【详解】解:(1)正方体浸没在水中,排开水的体积
正方体受到的浮力大小
(2)A和B处于漂浮状态,所以
则正方体B的重力
正方体B 的质量
正方体B的密度
答:(1)正方体受到的浮力的大小为10N;
(2)正方体的密度为。
5.(1)3000Pa;(2)10N;(3)0.6×103kg/m3
【详解】解:(1)此时水深
h=30cm=0.3m
水对容器底部的压强
p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa
(2)因为物块上表面与水面相平,则物块刚好完全浸没在水中,排开水的体积等于物块的体积,即
V排=V物=(0.1 m) 3 =1×10-3m3
物块所受的浮力
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N
(3)由图甲可知,当物块上表面与液面齐平时,物块上表面距容器底的距离为h=30cm,弹簧伸长的长度
ΔL=30cm-16cm-10cm=4cm
由图乙可知,此时弹簧对物体的拉力为
F拉=4N
木块的重力
G物=F浮-F拉=10N-4N=6N
木块的质量
物体的密度
答:(1)水对容器底部的压强为3000Pa;
(2)物块受到水的浮力为10N;
(3)物块的密度为0.6×103kg/m3。
6.(1)5N;(2)19.2N;(3)10cm,1020g
【详解】解:(1)由题知,剩余部分的质量为0.5kg,剩余部分放入水中恰好悬浮,此时受到的浮力
(2)注水到24cm时停止,水的深度
水对容器底部的压强
由得,水对容器底部的压力
(3)当注入水深度
时,物体恰好处于漂浮状态,由浮漂条件有
所以
即
①
剩余部分放入水中恰好悬浮时
即
②
①式-②式,化简解得
将代入②,解得
所以注入水的总体积为
由得,注水的质量
答:(1)剩余部分悬浮于水中时受到的浮力为5N;
(2)注水停止时水对容器底部的压力为19.2N;
(3)物体水平切掉的高度Δh为10cm,图乙中m2的值为1020g。
7.(1)0.6×103kg/m3;(2)4N;(3)
【详解】(1)由题意可知,木块的体积为
且其重力G=6N,由可得
根据密度公式可得
(2)因木块浸没则有V=V排,根据阿基米德原理可得
对木块进行受力分析可知其受到的拉力
(3)剪断细线后,木块最终处于漂浮状态有
F'浮=G=6N
与木块浸没相比其受到的浮力减小了4N,即柱形容器底部受到水的压力减小了4N,根据压强公式可得
答:(1)正方体木块的密度为0.6×103kg/m3;
(2)细绳对木块的拉力大小为4N;
(3)剪断细绳后木块A露出水面后,容器底受水的压强减少200Pa。
8.(1)600g;(2)10N;(3)1500Pa
【详解】解:(1)分析图可知,当物体完全浸没在水中时,杆对物体A的作用力向下,大小为4N,当物体开始露出液面,杆对物体向下的压力减小,在t1=5s时,杆对物体的压力为零,然后杆对物体产生向上的拉力,当t2=6.5s时,物体完全露出液面,杆对物体的拉力F2=6N,所以物体重力
物体的质量
(2)当物体完全浸没在水中时,受竖直向下的重力、杆向下的压力和竖直向上的浮力处于平衡状态,所以物体完全浸没时受到的浮力
(3)在t1=5s时,杆对物体的压力为零,此时所受浮力等于物体的重力,即
此时物体浸在液体中的体积
物体浸在液体中的深度
5s~6.5s过程中,物体排开的水的体积的变化量
水面下降的距离
因而物体在5s~6.5s过程中上升的距离
物体在5s~6.5s过程中运动的时间
所以物体运动的速度
在6.5s时,物体完全离开水面,物体与水相对运动的时间t2=6.5s,所以容器中水的深度
容器中水的体积
容器中水的重力
由图可知,5s~6.5s过程中,F与t成正比,其函数关系式可写为
当t=5s时,F=0;当t=6.5s时,F=6N;将数据带入解析式,得k=4,b= 20。得其关系式为
当t=6s时,杆对物体的拉力
此时物体所受浮力
所以当t5=6s时,容器对水平桌面的压力
容器对水平桌面的压强
答:(1)圆柱体A的质量为600g;
(2)圆柱体A浸没时受到的浮力为10N;
(3)第6s末容器对水平地面的压强为1500Pa。
9.(1)1200Pa;(2)5N;(3)2N
【详解】解:(1) A上表面所受水的压强
P=水gh=1103kg/m310N/kg0.12m=1200Pa
(2) B受到的浮力
(3)由阿基米德原理知道,A、B受到的总浮力是
F浮=水gV排=水g(VA+VB)=1103kg/m310N/kg(1.0103m3+0.5103m3)=15 N
又因为A、B恰好悬浮,所以
F浮=GA+GB
故 B的重力是
GB=F浮GA=15N8N=7N
细线对B的拉力是
F拉=GBF浮B=7N5N=2N
答:(1)A上表面所受水的压强为1200Pa;
(2)B受到的浮力为5N;
(3)细线对B的拉力大小2N。
10.(1)1.2×103Pa;(2)2.4kg;(3)84N
【详解】解:(1)水对容器底部的压强为
(2)由图乙知,当水的深度为h1=0.06m时,容器中加入的水的质量为m水1=1.2kg,当水的深度为h2=0.12m时,容器中加入的水的质量为m水2=4.8kg,当水的深度为h1=0.06m时,质量变化出现拐点,由于B的高度为10cm=0.1m,所以拐点时即为物体A、B恰好漂浮;则水的深度由h1到h2时,深度增加量为
容器中水的质量增加量为
由得,增加的水的体积为
则容器的底面积为
当水的深度为h1=0.06m时,由得
则B浸入水的体积为
则B的底面积为
由于A和B处于漂浮,则根据漂浮条件可知
则
(3)将A拿开后,B上升1cm=0.01m,此时B处于漂浮状态,所以
则B的质量为
所以A 的质量为
故水对容器底部压力的受力面积与容器对桌面压力的受力面积相同,故压强之比与压力之比也相同,当比值为1:2时,即
解得
m水=6kg
再把A放水中,则水对容器底部的压力为
答:(1)水对容器底部的压强为1.2×103Pa;
(2)物体A和B的总质量为2.4kg;
(3)此时水对容器底部的压力为84N。
11.(1)2.4×103Pa;(2)10N;(3)0.6×103kg/m3;(4)1.2kg
【详解】解:(1)容器底部受到水的压强
p=ρ水gh=1.0×103kg/m3×10N/kg×0.24m=2.4×103Pa
(2)因为木块上表面与水面相平,所以木块浸没在水中,木块排开水的体积等于木块的体积,木块受到的浮力
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×(0.1m)3=10N
(3)由于弹簧原长10cm,木块边长10cm,水深24cm,所以弹簧伸长
ΔL=h水深﹣L弹簧﹣L木块=24cm﹣10cm﹣10cm=4cm
由图乙可知,当弹簧伸长4cm时,弹簧对木块的拉力F=4N,此时木块受到重力、浮力和弹簧对木块的拉力三个力作用,且木块处于静止状态,所以
F浮=G木块+F拉力
木块的重力
G木块=F浮﹣F拉力=10N﹣4N=6N
木块的质量
木块的密度
(4)放水前,水的体积
V水=V总﹣V木块=S容器h﹣V木块=200cm2×24cm﹣(10cm)3=3800cm3
由当弹簧处于没有发生形变的自然状态时,木块受到的浮力等于木块的重力,木块受到的浮力
F浮′=G木块=6N
木块排开水的体积
此时木块浸入水中的深度
此时水的深度等于弹簧原长与木块浸入水中的深度之和,即水的深度
h水=10cm+6cm=16cm=0.16m
水的体积
V水′=V总′﹣V排′=S容器h水﹣V排′=200×10﹣4m2×0.16m﹣6×10﹣4m3=26×10﹣4m3=2600cm3
放出的水的体积
V放水=V水﹣V水′=3800cm3﹣2600cm3=1200cm3
放出的水的质量
m=ρ水V放水=1.0g/cm3×1200cm3=1200g=1.2kg
答:(1)容器底部受到水的压强是2.4×103Pa;
(2)木块受到的浮力是10N;
(3)木块的密度是0.6×103kg/m3;
(4)放出的水的质量是1.2kg。
12.(1)5000N;(2)0.25m2;(3)2.5×103 kg/m3
【详解】解:(1)由图像可知,石柱下表面离开水面后受到的拉力,因石柱匀速上升时处于平衡状态,受到的重力和拉力是一对平衡力,所以,石柱的重力为
由图像可知,石柱浸没时受到的拉力,则由称重法,石柱浸没在水中受到的浮力
(2)因为忽略液面高度的变化,则石柱的高度为
石柱浸没在水中时,排开水的体积等于石柱的体积,石柱的体积为
则石柱的底面积为
(3)由可知,长方体石柱的密度为
答:(1)长方体石柱浸没时在水中所受的浮力为5000N;
(2)长方体石柱的底面积为;
(3)长方体石柱的密度为。
13.(1)5N;(2)250Pa;(3)6×103kg/m3
【详解】解:(1)由题意可知,甲中玻璃杯A处于漂浮状态,其受到的浮力和自身的重力相等,所以,玻璃杯A受到的浮力
F浮=GA=5N
(2)玻璃杯A漂浮,根据浮力产生的原因可知,水对玻璃杯A底部的压力
F=F浮=5N
则玻璃杯A底部受到水的压强
(3)由图乙可知当金属块B被提起时绳子的拉力F=2N,金属块B浸没在水中排开水的体积
VB排=VB=4×10-5m3
则金属块B受到浮力
FB浮=ρ水gVB排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N
因金属块B受到竖直向下的重力、竖直向上的浮力和拉力,且金属块受平衡力,所以金属块B的重力
GB=FB浮+F拉=0.4N+2N=2.4N
由G=mg可知,金属块B的质量
则金属块B的密度
答:(1)图甲中玻璃杯A所受浮力的大小为5N;
(2)图甲中水对玻璃杯A底部的压强大小250Pa;
(3)实心金属块B的密度为6×103kg/m3。
答案第1页,共2页
答案第1页,共2页
1.如图甲所示,一柱形物体通过绳子与轻质弹簧悬挂于O点,物体浸没于装水的薄柱形容器中,上表面恰好与水面相平,阀门K处于关闭状态,弹簧所受拉力F与其伸长量 x的关系如图乙所示。已知容器置于水平地面上,其底面积为200cm2,容器中水深20cm,物体的底面积为100cm2,高为10cm,重为15N。容器及绳子重力忽略不计,ρ水=1.0×103kg/m3。求;
(1)物体所受的浮力大小;
(2)容器对水平地面的压强大小;
(3)打开阀门K放出烧杯内的水,当柱形物体有一半露出水面时,容器底部所受的液体压强的大小。
2.将足够高的薄壁柱形容器甲、乙放置在水平地面上,如图所示,甲、乙两容器中分别盛有深度为0.1米的酒精和质量为1千克的水。已知容器乙的底面积为米2,酒精的密度为千克/米3.
(1)求水的体积。
(2)现将密度为千克/米3的小球放入某个容器内,小球浸没于液体中,此时两液体对容器底部的压强恰好相等,求该容器对地面压强的增加量。
3.如图所示,质量为0.81kg的物体A以及甲、乙两个高度相同的轻质薄壁容器置于水平桌面上,甲、乙容器的底面积分别为S甲=1×10-2m2、S乙=5×10-3m2。现分别向甲、乙两个容器中倒入质量相同的酒精和水,甲中酒精的深度为10cm,乙中水的深度为16cm(g=10N/kg,酒=0.8×103kg/m3,水=1.0×103kg/m3)。求:
(1)若物体A的底面积为5×10-3m2,物体A对水平地面的压强;
(2)乙容器中水对容器底部的压力;
(3)若将物块A浸入甲容器的酒精中,甲容器的液面刚好和乙容器中的液面相平,求物块A的最大密度。
4.如图所示,正方体的边长为,在它的上面放一个重为2N的物体,此时正方体恰好没入水中,已知。求:(g取10 N/kg)
(1)正方体B受到的浮力的大小;
(2)正方体B的密度。
5.如图甲所示,一轻质弹簧,其两端分别固定在容器底部和正方体物块上。已知物块的边长为10cm,弹簧没有发生形变时的长度为16cm,弹簧受到拉力作用后,伸长的长度ΔL与拉力F的关系如图乙所示。向容器中加水,直到物块上表面与水面相平,此时水深30cm。求:(ρ水=1.0×103kg/m3,g取10N/kg)
(1)水对容器底部的压强;
(2)物块受到水的浮力;
(3)物块的密度。
6.一底面积为80cm 的容器放置在水平地面上(如图甲所示),内放有一柱形物体。物体是由高20cm、底部嵌有金属块的塑料制成。缓慢向图甲所示容器中注水到一定深度时物体会漂浮,继续注水到24cm时停止,注水质量m与容器中水的深度h的关系图像如图乙所示。当把物体水平切掉一部分后,剩余部分放入水中恰好悬浮(如图丙所示),测得物体剩余部分的质量为0.5kg。(、)求:
(1)剩余部分悬浮于水中时受到的浮力;
(2)注水停止时水对容器底部的压力;
(3)物体水平切掉的高度Δh和图乙中m2的值。
7.如图所示,水平放置的平底薄壁柱形容器底面积是200cm2,内装有一些水,一个不吸水的实心正方体木块A边长为10cm,重为6N,用细绳一端系住木块A另一端固定在容器底部使木块A浸没水中。(细绳的体积和质量均不计,ρ水=1.0×103kg/m3;g值取10N/kg)求:
(1)该正方体木块的密度;
(2)细绳对木块的拉力大小;
(3)剪断细绳后木块A露出水面后,容器底受水的压强减少多少帕斯卡?
8.如图甲所示,水平地面上有一底面积为200cm2、重为2N、盛水的薄壁柱形容器。底面积为100cm2的圆柱体A,上表面中央沿竖直方向固定一根体积不计的细杆,下表面刚好接触容器底部。现将圆柱体A通过细杆竖直向上匀速取出,细杆对圆柱体A的作用力F的大小与时间t的关系图像如图乙所示。求:
(1)圆柱体A的质量为多少g?
(2)圆柱体A浸没时受到的浮力为多少N?
(3)第6s末容器对水平地面的压强为多少Pa?
9.如图,用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮。此时的上表面到水面的高度差为。已知A的体积为,所受重力为;B的体积为,水的密度取,求:
(1)A上表面所受水的压强;
(2)B受到的浮力;
(3)细线对B的拉力大小。
10.如图甲所示,足够高质量为8kg的长方体容器C置于水平地面,不吸水的AB两物体叠放置于容器内,A为正方体,B为长方体,其中A的边长为10cm,B的高为0.1m,缓慢向容器中加水,直到容器中水的深度为0.12m时停止加水,所加水的质量与容器中水的深度关系如图乙所示,已知ρ水=1.0×103kg/cm3,g=10N/kg,求:
(1)停止加水时,水对容器底部的压强;
(2)物体A和B的总质量为多少kg;
(3)停止加水后,将物体A拿开,物体B相对于水面上升1cm,接着继续向容器中继续注水,当水对容器底部的压强与容器对桌面的压强之比为1:2时,再将A物体放入水中,此时水对容器底部的压力为多少N。(设物体上、下表面始终与水面平行)
11.有一体积、质量忽略不计的弹簧,其原长为10cm,把弹簧下端固定在容器底部,容器底面积200cm2,上端固定在边长为10cm的正方体木块上,向容器中加水直到木块上表面与液面相平,如图甲所示,此时水深为24cm。弹簧受到拉力作用时,弹簧伸长的长度ΔL与所受拉力F的关系如图乙所示。(ρ水=1.0×103kg/m3)求:
(1)水深为24cm时容器底部受到水的压强;
(2)木块受到水的浮力;
(3)木块的密度;
(4)打开出水孔,缓慢放水,当弹簧处于没有发生形变的自然状态时,关闭出水孔,此时放出水的质量。
12.某水底打捞作业中,需将一长方体石柱从水底匀速打捞出水,如图所示是吊车钢丝绳拉力F随石柱下表面距水底深度h变化的图像,水的阻力和液面变化忽略不计,求:
(1)长方体石柱浸没时在水中所受的浮力;
(2)长方体石柱的底面积;
(3)长方体石柱的密度。
13.如图甲所示,在水平桌面上放有一薄壁柱形容器,一个重力为5N,底面积为0.02m2,高为10cm的柱形玻璃杯A漂浮于水面,在A的底部连接有一个体积为4×10-5m3的实心金属块B。此时A、B两物体在水中处于静止状态,细线未拉直(B未与容器底部紧密接触,细线不可伸长且质量、体积忽略不计)。向容器中注水,细线拉力随时间变化的图象如图乙所示(容器足够高)。(水密度为1.0×103kg/m3,g取10N/kg)求:
(1)图甲中玻璃杯A所受浮力的大小;
(2)图甲中水对玻璃杯A底部的压强大小;
(3)实心金属块B的密度。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)10N;(2);(3)
【详解】解:(1)物体的体积为
物体浸没在水中所受的浮力大小为
(2)容器中水的体积为
水的重力为
物体间作用力是相互的,容器对桌面的压力为
容器对水平地面的压强为
(3)当柱形物体有一半露出水面时,减小的浮力为
根据,弹簧测力计的示数增大5N,如图所示,弹簧长度增大2.5cm,即物体下降2.5cm,此时的液面深度为
容器底部所受的液体压强为
答:(1)物体所受的浮力为10N;
(2)容器对水平地面的压强为;
(3)打开阀门K放出烧杯内的水,当柱形物体有一半露出水面时,容器底部所受的液体压强为。
2.(1)1×10-3m3;(2)500Pa
【详解】解:(1)水的体积
(2)酒精对容器底的压强
水对容器底的压强
由于p甲
答:(1)水的体积为1×10-3m3;
(2)该容器对地面压强的增加量为500Pa。
3.(1)1.62×103pa;(2)8N;(3)1.35×103kg/m3
【详解】解(1)在平面上物体的压力大小等于重力大小,所以压力为
则物体A对水平地面的压强
(2)乙容器中水对容器底部的压强为
则乙容器中水对容器底部的压力为
(3)浸入甲容器的物块,当物体浸没时物块的体积最小,则其密度最大,由于甲容器的液体进入物块后,甲容器的液面刚好和乙容器中的液面相平,则此时甲容器的液体深度为
物块的最小体积
所以物块A的最大密度为
答:(1)物体A对水平地面的压强为1.62×103pa;
(2)乙容器中水对容器底部的压力为8N;
(3)物块A的最大密度为1.35×103kg/m3。
4.(1)10N;(2)
【详解】解:(1)正方体浸没在水中,排开水的体积
正方体受到的浮力大小
(2)A和B处于漂浮状态,所以
则正方体B的重力
正方体B 的质量
正方体B的密度
答:(1)正方体受到的浮力的大小为10N;
(2)正方体的密度为。
5.(1)3000Pa;(2)10N;(3)0.6×103kg/m3
【详解】解:(1)此时水深
h=30cm=0.3m
水对容器底部的压强
p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa
(2)因为物块上表面与水面相平,则物块刚好完全浸没在水中,排开水的体积等于物块的体积,即
V排=V物=(0.1 m) 3 =1×10-3m3
物块所受的浮力
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N
(3)由图甲可知,当物块上表面与液面齐平时,物块上表面距容器底的距离为h=30cm,弹簧伸长的长度
ΔL=30cm-16cm-10cm=4cm
由图乙可知,此时弹簧对物体的拉力为
F拉=4N
木块的重力
G物=F浮-F拉=10N-4N=6N
木块的质量
物体的密度
答:(1)水对容器底部的压强为3000Pa;
(2)物块受到水的浮力为10N;
(3)物块的密度为0.6×103kg/m3。
6.(1)5N;(2)19.2N;(3)10cm,1020g
【详解】解:(1)由题知,剩余部分的质量为0.5kg,剩余部分放入水中恰好悬浮,此时受到的浮力
(2)注水到24cm时停止,水的深度
水对容器底部的压强
由得,水对容器底部的压力
(3)当注入水深度
时,物体恰好处于漂浮状态,由浮漂条件有
所以
即
①
剩余部分放入水中恰好悬浮时
即
②
①式-②式,化简解得
将代入②,解得
所以注入水的总体积为
由得,注水的质量
答:(1)剩余部分悬浮于水中时受到的浮力为5N;
(2)注水停止时水对容器底部的压力为19.2N;
(3)物体水平切掉的高度Δh为10cm,图乙中m2的值为1020g。
7.(1)0.6×103kg/m3;(2)4N;(3)
【详解】(1)由题意可知,木块的体积为
且其重力G=6N,由可得
根据密度公式可得
(2)因木块浸没则有V=V排,根据阿基米德原理可得
对木块进行受力分析可知其受到的拉力
(3)剪断细线后,木块最终处于漂浮状态有
F'浮=G=6N
与木块浸没相比其受到的浮力减小了4N,即柱形容器底部受到水的压力减小了4N,根据压强公式可得
答:(1)正方体木块的密度为0.6×103kg/m3;
(2)细绳对木块的拉力大小为4N;
(3)剪断细绳后木块A露出水面后,容器底受水的压强减少200Pa。
8.(1)600g;(2)10N;(3)1500Pa
【详解】解:(1)分析图可知,当物体完全浸没在水中时,杆对物体A的作用力向下,大小为4N,当物体开始露出液面,杆对物体向下的压力减小,在t1=5s时,杆对物体的压力为零,然后杆对物体产生向上的拉力,当t2=6.5s时,物体完全露出液面,杆对物体的拉力F2=6N,所以物体重力
物体的质量
(2)当物体完全浸没在水中时,受竖直向下的重力、杆向下的压力和竖直向上的浮力处于平衡状态,所以物体完全浸没时受到的浮力
(3)在t1=5s时,杆对物体的压力为零,此时所受浮力等于物体的重力,即
此时物体浸在液体中的体积
物体浸在液体中的深度
5s~6.5s过程中,物体排开的水的体积的变化量
水面下降的距离
因而物体在5s~6.5s过程中上升的距离
物体在5s~6.5s过程中运动的时间
所以物体运动的速度
在6.5s时,物体完全离开水面,物体与水相对运动的时间t2=6.5s,所以容器中水的深度
容器中水的体积
容器中水的重力
由图可知,5s~6.5s过程中,F与t成正比,其函数关系式可写为
当t=5s时,F=0;当t=6.5s时,F=6N;将数据带入解析式,得k=4,b= 20。得其关系式为
当t=6s时,杆对物体的拉力
此时物体所受浮力
所以当t5=6s时,容器对水平桌面的压力
容器对水平桌面的压强
答:(1)圆柱体A的质量为600g;
(2)圆柱体A浸没时受到的浮力为10N;
(3)第6s末容器对水平地面的压强为1500Pa。
9.(1)1200Pa;(2)5N;(3)2N
【详解】解:(1) A上表面所受水的压强
P=水gh=1103kg/m310N/kg0.12m=1200Pa
(2) B受到的浮力
(3)由阿基米德原理知道,A、B受到的总浮力是
F浮=水gV排=水g(VA+VB)=1103kg/m310N/kg(1.0103m3+0.5103m3)=15 N
又因为A、B恰好悬浮,所以
F浮=GA+GB
故 B的重力是
GB=F浮GA=15N8N=7N
细线对B的拉力是
F拉=GBF浮B=7N5N=2N
答:(1)A上表面所受水的压强为1200Pa;
(2)B受到的浮力为5N;
(3)细线对B的拉力大小2N。
10.(1)1.2×103Pa;(2)2.4kg;(3)84N
【详解】解:(1)水对容器底部的压强为
(2)由图乙知,当水的深度为h1=0.06m时,容器中加入的水的质量为m水1=1.2kg,当水的深度为h2=0.12m时,容器中加入的水的质量为m水2=4.8kg,当水的深度为h1=0.06m时,质量变化出现拐点,由于B的高度为10cm=0.1m,所以拐点时即为物体A、B恰好漂浮;则水的深度由h1到h2时,深度增加量为
容器中水的质量增加量为
由得,增加的水的体积为
则容器的底面积为
当水的深度为h1=0.06m时,由得
则B浸入水的体积为
则B的底面积为
由于A和B处于漂浮,则根据漂浮条件可知
则
(3)将A拿开后,B上升1cm=0.01m,此时B处于漂浮状态,所以
则B的质量为
所以A 的质量为
故水对容器底部压力的受力面积与容器对桌面压力的受力面积相同,故压强之比与压力之比也相同,当比值为1:2时,即
解得
m水=6kg
再把A放水中,则水对容器底部的压力为
答:(1)水对容器底部的压强为1.2×103Pa;
(2)物体A和B的总质量为2.4kg;
(3)此时水对容器底部的压力为84N。
11.(1)2.4×103Pa;(2)10N;(3)0.6×103kg/m3;(4)1.2kg
【详解】解:(1)容器底部受到水的压强
p=ρ水gh=1.0×103kg/m3×10N/kg×0.24m=2.4×103Pa
(2)因为木块上表面与水面相平,所以木块浸没在水中,木块排开水的体积等于木块的体积,木块受到的浮力
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×(0.1m)3=10N
(3)由于弹簧原长10cm,木块边长10cm,水深24cm,所以弹簧伸长
ΔL=h水深﹣L弹簧﹣L木块=24cm﹣10cm﹣10cm=4cm
由图乙可知,当弹簧伸长4cm时,弹簧对木块的拉力F=4N,此时木块受到重力、浮力和弹簧对木块的拉力三个力作用,且木块处于静止状态,所以
F浮=G木块+F拉力
木块的重力
G木块=F浮﹣F拉力=10N﹣4N=6N
木块的质量
木块的密度
(4)放水前,水的体积
V水=V总﹣V木块=S容器h﹣V木块=200cm2×24cm﹣(10cm)3=3800cm3
由当弹簧处于没有发生形变的自然状态时,木块受到的浮力等于木块的重力,木块受到的浮力
F浮′=G木块=6N
木块排开水的体积
此时木块浸入水中的深度
此时水的深度等于弹簧原长与木块浸入水中的深度之和,即水的深度
h水=10cm+6cm=16cm=0.16m
水的体积
V水′=V总′﹣V排′=S容器h水﹣V排′=200×10﹣4m2×0.16m﹣6×10﹣4m3=26×10﹣4m3=2600cm3
放出的水的体积
V放水=V水﹣V水′=3800cm3﹣2600cm3=1200cm3
放出的水的质量
m=ρ水V放水=1.0g/cm3×1200cm3=1200g=1.2kg
答:(1)容器底部受到水的压强是2.4×103Pa;
(2)木块受到的浮力是10N;
(3)木块的密度是0.6×103kg/m3;
(4)放出的水的质量是1.2kg。
12.(1)5000N;(2)0.25m2;(3)2.5×103 kg/m3
【详解】解:(1)由图像可知,石柱下表面离开水面后受到的拉力,因石柱匀速上升时处于平衡状态,受到的重力和拉力是一对平衡力,所以,石柱的重力为
由图像可知,石柱浸没时受到的拉力,则由称重法,石柱浸没在水中受到的浮力
(2)因为忽略液面高度的变化,则石柱的高度为
石柱浸没在水中时,排开水的体积等于石柱的体积,石柱的体积为
则石柱的底面积为
(3)由可知,长方体石柱的密度为
答:(1)长方体石柱浸没时在水中所受的浮力为5000N;
(2)长方体石柱的底面积为;
(3)长方体石柱的密度为。
13.(1)5N;(2)250Pa;(3)6×103kg/m3
【详解】解:(1)由题意可知,甲中玻璃杯A处于漂浮状态,其受到的浮力和自身的重力相等,所以,玻璃杯A受到的浮力
F浮=GA=5N
(2)玻璃杯A漂浮,根据浮力产生的原因可知,水对玻璃杯A底部的压力
F=F浮=5N
则玻璃杯A底部受到水的压强
(3)由图乙可知当金属块B被提起时绳子的拉力F=2N,金属块B浸没在水中排开水的体积
VB排=VB=4×10-5m3
则金属块B受到浮力
FB浮=ρ水gVB排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N
因金属块B受到竖直向下的重力、竖直向上的浮力和拉力,且金属块受平衡力,所以金属块B的重力
GB=FB浮+F拉=0.4N+2N=2.4N
由G=mg可知,金属块B的质量
则金属块B的密度
答:(1)图甲中玻璃杯A所受浮力的大小为5N;
(2)图甲中水对玻璃杯A底部的压强大小250Pa;
(3)实心金属块B的密度为6×103kg/m3。
答案第1页,共2页
答案第1页,共2页
