六年级下册数学苏教版第二单元 圆柱与圆锥整理与练习课件(共28张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第二单元 圆柱与圆锥整理与练习课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 14:39:46 | ||
图片预览






文档简介
(共28张PPT)
苏教版小学数学六年级下册 第二单元 圆柱和圆锥
整理与练习(1)
回顾与整理
小组讨论:
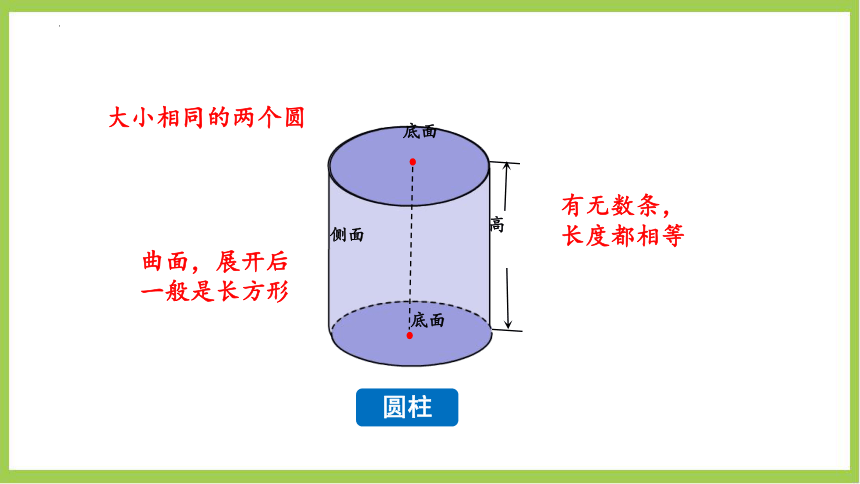
1.圆柱和圆锥各有哪些特征?
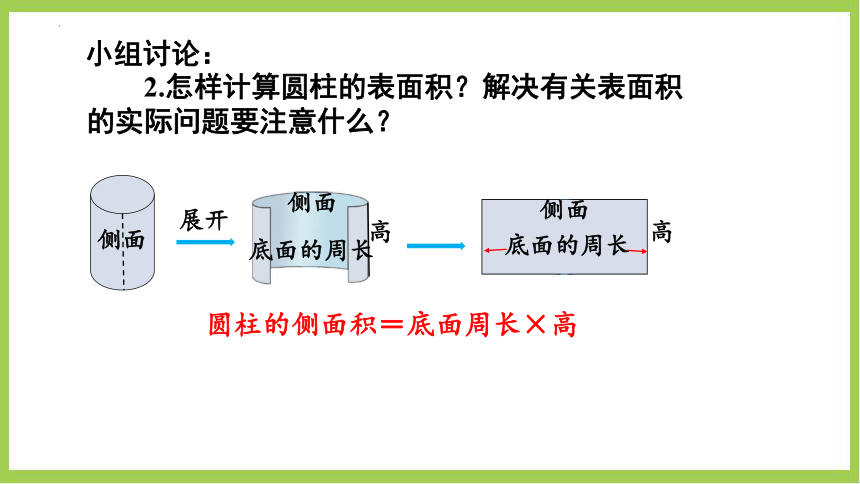
2.怎样计算圆柱的表面积?解决有关表面积的实际问题要注意什么?
3.我们是怎样发现圆柱、圆锥体积公式的?圆柱和圆锥的体积公式之间有什么联系?
有无数条,长度都相等
侧面
底面
底面
高
大小相同的两个圆
曲面,展开后一般是长方形
圆柱
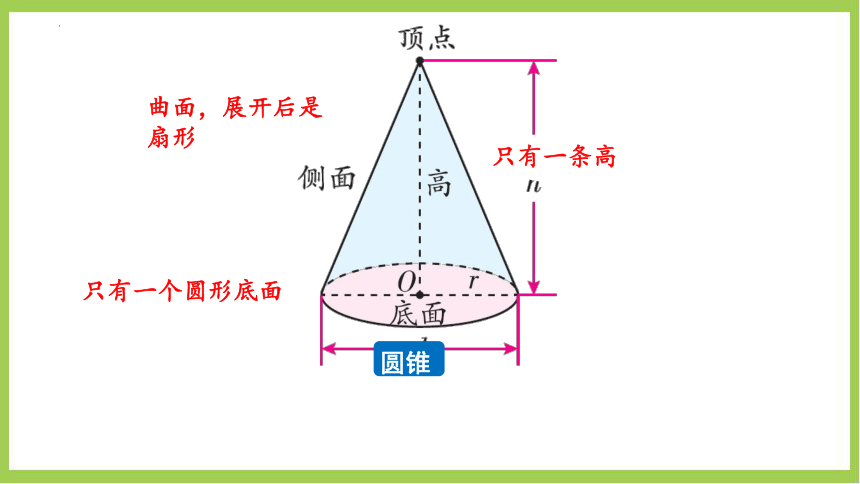
圆锥
只有一条高
只有一个圆形底面
曲面,展开后是扇形
圆柱和圆锥的特征
小组讨论:
2.怎样计算圆柱的表面积?解决有关表面积的实际问题要注意什么?
展开
侧面
底面的周长
高
底面的周长
高
侧面
侧面
圆柱的侧面积=底面周长×高
圆柱的表面积
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
1
利用直径计算:S表=πdh+2π(d÷2)2
3
利用半径计算:S表=2πrh+ 2πr2
2
圆柱的体积=圆柱的底面积×高
圆柱的体积计算
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
圆锥的体积
通过实验,发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系。
V= Sh= πr h
圆柱和圆锥
练习与应用
(教材第24页)
1.算一算,填一填。
4cm
5m
87.92cm2
62.8cm3
408.2m2
628m3
2.5cm
7.85cm3
1.2m
0.67824m3
2.一种压路机的前轮是圆柱形的,轮宽1.6米,直径是0.8米。前轮滚动一周,压路的面积是多少平方米?
滚动一个底面周长的长度,相当于把它的侧面展开后平铺在路面上。
3.14×0.8×1.6=4.0192(平方米)
答:压路的面积是4.0192平方米。
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
15.7÷3.14÷2=2.5(分米)
15.7×6=94.2(平方分米)
3.14×2.52=19.625(平方分米)
94.2+19.625=113.825(平方分米)
答:做这个水桶至少要用模板113.825平方分米。
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约长15.7分米。
(2)这个水桶能盛120升水吗?
19.625×6=117.75(立方分米)
117.75立方分米=117.75升
117.75<120
答:这个水桶不能盛120升水。
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?(得数保留整数)
6.28×0.55≈3(吨)
答:这堆稻谷大约重3吨。
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
答:高是18厘米。
6×3=18(厘米)
(2)把它捏成高是6厘米的圆锥形,底面积是多少平方厘米?
答:底面积是45平方厘米。
15×3=45(平方厘米)
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
3.14×(6÷2)2×12=339.12(立方厘米)
方法一:
113.04+339.12=452.16(立方厘米)
方法二:
3.14×(6÷2)2×12=339.12(立方厘米)
339.12÷3=113.04(立方厘米)
113.04+339.12=452.16(立方厘米)
答:它们的体积一共是452.16立方厘米。
7.
12
21
2
8.有两个不同形状的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米,高是10厘米;长方体装饰瓶的长和宽都是11厘米,高是9厘米。
哪个装饰瓶里的五彩石多一些?
圆柱体:3.14×(10÷2)2×10=785(立方厘米)
长方体:11×11×9=1089(立方厘米)
785<1089
答:长方体装饰瓶里的五彩石多一些。
9.一根自来水管的内直径是20 毫米。如果水流的速度是0.8米/秒,这根水管1 分钟可以流出多少升水?
3.14×(20÷2)2=314(平方毫米)
314平方毫米=0.000314平方米
0.000314×0.8×60=0.015072(立方米)
0.015072立方米=15.072升
答:这根水管1 分钟可以流出15.072升水。
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
9.6÷7.5÷4=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱(如图)。
(1)纸箱的长、宽、高至少各是多少厘米?
(2)纸箱的容积至少是多少立方厘米?
(3)做一个这样的纸箱,至少要用硬纸板多少平方厘米?
(箱盖和箱底的重叠部分按2000平方厘米计算)
探索与实践
(教材第26页)
12.有两个圆柱形容器,它们的高相等,底面半径的比是1∶2。它们的体积的比是几比几?
12∶22=1∶4
答:它们的体积的比是1比4。
13.选择一种圆柱形饮料罐,测量有关数据,计算出它的容积。再与商标纸上标出的容积比一比,你能发现什么?
测量时要注意什么?
用容器盛装液体时,一般都要留有一定的空隙,所以,饮料罐里装的液体的体积一般都会比它的实际容积要小,也比饮料罐的体积小。
14.选一张长方形纸,卷成两个大小不同的圆柱,分别算出体积。与同学交流,怎样卷圆柱的体积比较大?
以长方形的长为底面周长卷成的圆柱的体积比较大。
评价与反思
(教材第26页)
根据自己的表现,能得几个 ,就把几个 涂上颜色。
我国古代劳动人民早在2000多年前,就会计算不同形状物体的体积。《九章算术》中记载的圆柱体积计算方法是“周自相乘,以高乘之,十二而一”,也就是底面周长的平方乘高,再除以12。这种计算方法与现在的算法是一致的,只不过取圆周率的近似值为3。书中记载的圆锥体积计算方法,也与现在的算法一致。
苏教版小学数学六年级下册 第二单元 圆柱和圆锥
整理与练习(1)
回顾与整理
小组讨论:
1.圆柱和圆锥各有哪些特征?
2.怎样计算圆柱的表面积?解决有关表面积的实际问题要注意什么?
3.我们是怎样发现圆柱、圆锥体积公式的?圆柱和圆锥的体积公式之间有什么联系?
有无数条,长度都相等
侧面
底面
底面
高
大小相同的两个圆
曲面,展开后一般是长方形
圆柱
圆锥
只有一条高
只有一个圆形底面
曲面,展开后是扇形
圆柱和圆锥的特征
小组讨论:
2.怎样计算圆柱的表面积?解决有关表面积的实际问题要注意什么?
展开
侧面
底面的周长
高
底面的周长
高
侧面
侧面
圆柱的侧面积=底面周长×高
圆柱的表面积
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
1
利用直径计算:S表=πdh+2π(d÷2)2
3
利用半径计算:S表=2πrh+ 2πr2
2
圆柱的体积=圆柱的底面积×高
圆柱的体积计算
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
1
利用直径计算:V=π(d÷2)2h
3
利用半径计算:V=πr2h
2
圆锥的体积
通过实验,发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系。
V= Sh= πr h
圆柱和圆锥
练习与应用
(教材第24页)
1.算一算,填一填。
4cm
5m
87.92cm2
62.8cm3
408.2m2
628m3
2.5cm
7.85cm3
1.2m
0.67824m3
2.一种压路机的前轮是圆柱形的,轮宽1.6米,直径是0.8米。前轮滚动一周,压路的面积是多少平方米?
滚动一个底面周长的长度,相当于把它的侧面展开后平铺在路面上。
3.14×0.8×1.6=4.0192(平方米)
答:压路的面积是4.0192平方米。
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
15.7÷3.14÷2=2.5(分米)
15.7×6=94.2(平方分米)
3.14×2.52=19.625(平方分米)
94.2+19.625=113.825(平方分米)
答:做这个水桶至少要用模板113.825平方分米。
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约长15.7分米。
(2)这个水桶能盛120升水吗?
19.625×6=117.75(立方分米)
117.75立方分米=117.75升
117.75<120
答:这个水桶不能盛120升水。
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?(得数保留整数)
6.28×0.55≈3(吨)
答:这堆稻谷大约重3吨。
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
答:高是18厘米。
6×3=18(厘米)
(2)把它捏成高是6厘米的圆锥形,底面积是多少平方厘米?
答:底面积是45平方厘米。
15×3=45(平方厘米)
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
3.14×(6÷2)2×12=339.12(立方厘米)
方法一:
113.04+339.12=452.16(立方厘米)
方法二:
3.14×(6÷2)2×12=339.12(立方厘米)
339.12÷3=113.04(立方厘米)
113.04+339.12=452.16(立方厘米)
答:它们的体积一共是452.16立方厘米。
7.
12
21
2
8.有两个不同形状的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米,高是10厘米;长方体装饰瓶的长和宽都是11厘米,高是9厘米。
哪个装饰瓶里的五彩石多一些?
圆柱体:3.14×(10÷2)2×10=785(立方厘米)
长方体:11×11×9=1089(立方厘米)
785<1089
答:长方体装饰瓶里的五彩石多一些。
9.一根自来水管的内直径是20 毫米。如果水流的速度是0.8米/秒,这根水管1 分钟可以流出多少升水?
3.14×(20÷2)2=314(平方毫米)
314平方毫米=0.000314平方米
0.000314×0.8×60=0.015072(立方米)
0.015072立方米=15.072升
答:这根水管1 分钟可以流出15.072升水。
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
9.6÷7.5÷4=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱(如图)。
(1)纸箱的长、宽、高至少各是多少厘米?
(2)纸箱的容积至少是多少立方厘米?
(3)做一个这样的纸箱,至少要用硬纸板多少平方厘米?
(箱盖和箱底的重叠部分按2000平方厘米计算)
探索与实践
(教材第26页)
12.有两个圆柱形容器,它们的高相等,底面半径的比是1∶2。它们的体积的比是几比几?
12∶22=1∶4
答:它们的体积的比是1比4。
13.选择一种圆柱形饮料罐,测量有关数据,计算出它的容积。再与商标纸上标出的容积比一比,你能发现什么?
测量时要注意什么?
用容器盛装液体时,一般都要留有一定的空隙,所以,饮料罐里装的液体的体积一般都会比它的实际容积要小,也比饮料罐的体积小。
14.选一张长方形纸,卷成两个大小不同的圆柱,分别算出体积。与同学交流,怎样卷圆柱的体积比较大?
以长方形的长为底面周长卷成的圆柱的体积比较大。
评价与反思
(教材第26页)
根据自己的表现,能得几个 ,就把几个 涂上颜色。
我国古代劳动人民早在2000多年前,就会计算不同形状物体的体积。《九章算术》中记载的圆柱体积计算方法是“周自相乘,以高乘之,十二而一”,也就是底面周长的平方乘高,再除以12。这种计算方法与现在的算法是一致的,只不过取圆周率的近似值为3。书中记载的圆锥体积计算方法,也与现在的算法一致。
