5 三角形 单元练习卷 人教版数学 四年级下册(含解析)
文档属性
| 名称 | 5 三角形 单元练习卷 人教版数学 四年级下册(含解析) | 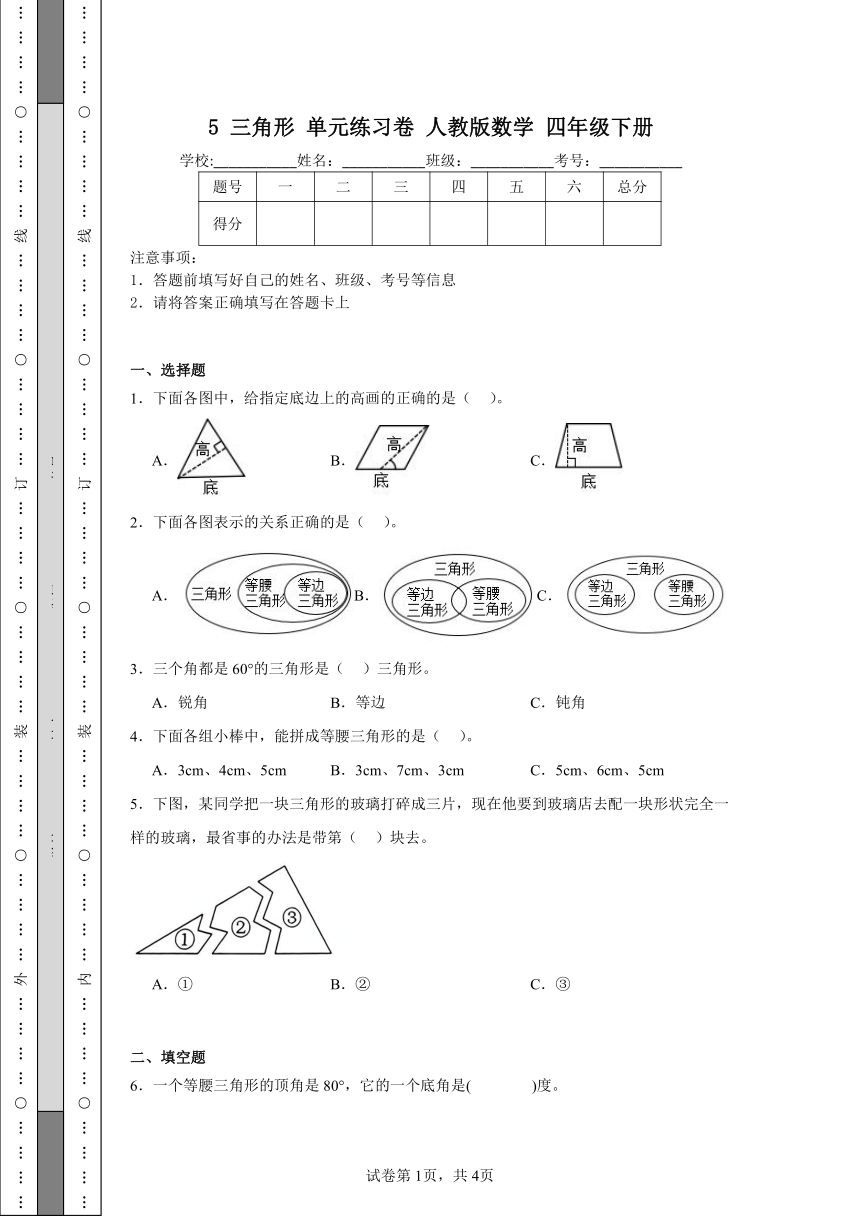 | |
| 格式 | docx | ||
| 文件大小 | 231.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 14:47:28 | ||
图片预览




文档简介
5 三角形 单元练习卷 人教版数学 四年级下册
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.下面各图中,给指定底边上的高画的正确的是( )。
A. B. C.
2.下面各图表示的关系正确的是( )。
A.B.C.
3.三个角都是60°的三角形是( )三角形。
A.锐角 B.等边 C.钝角
4.下面各组小棒中,能拼成等腰三角形的是( )。
A.3cm、4cm、5cm B.3cm、7cm、3cm C.5cm、6cm、5cm
5.下图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,最省事的办法是带第( )块去。
A.① B.② C.③
二、填空题
6.一个等腰三角形的顶角是80°,它的一个底角是( )度。
7.一个等腰三角形的一条边长是8厘米,另一条边长是3厘米,这个等腰三角形的周长是( )厘米。
8.当梯形的上底逐渐缩短到一个点时,梯形就转化成( )形,当梯形的上底增大到与下底相等时,梯形就转化成( )形。
9.如下图,三角形ABC是( )三角形,直角边BC对应的高是( ),BD是( )边对应的高。已知∠1=52°,那么∠2=( )°。
10.下图中的∠1=( )°,∠2=( )°。
三、判断题
11.高压电线杆上的支架做成三角形,是因为三角形具有稳定性。( )
12.任意一个三角形都可以分成两个直角三角形。( )
13.等腰三角形和等边三角形的关系是。( )
14.一个三角形中最小的角是46度,它一定是一个锐角三角形。( )
15.一个等腰三角形,其中两条边的长分别是8cm和4cm,则这个三角形的周长可能是20cm,也可能是16cm。( )
四、计算题
16.求出下面∠1的度数。
五、作图题
17.画出下面三角形指定底边上的高。
六、解答题
18.小熊要回家,走哪条路最近?为什么?
19.仔细观察下图,说一说图中一共有几个三角形?
20.一根铁丝可以围成一个腰长12厘米,底长18厘米的等腰三角形,如果改围一个等边三角形,那么等边三角形的边长是多少厘米?
21.某同学用一根180厘米长的铁丝围一个等腰三角形,经测量一条腰长为46厘米,底边长为多少厘米?
22.李爷爷有一块三角形蔬菜地,蔬菜地的最大角是,是最小角的4倍,这块三角形蔬菜地其他两个角各是多少度?按边分,这是一块什么三角形蔬菜地?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;从平行四边形或者梯形中互相平行的一组对边中的一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做它的高,垂足所在的边叫做底,据此解答。
【详解】由分析得,
A.底和高不是对应的,此题错误;
B.高不是垂直线段,此题错误;
C.底和高是对应的,此题正确。
故选:C
【点睛】此题考查的是平面图形的高的画法,解答此题应注意底和高必须是对应的。
2.A
【分析】根据三角形、等腰三角形和等边三角形的含义可知:等边三角形是特殊的等腰三角形,等腰三角形是特殊的三角形;由此解答即可。
【详解】A.三角形按边可以分为:不等边的三角形和等腰三角形,而等边三角形是特殊的等腰三角形,即等腰三角形包含了等边三角形,故包含关系正确;
B.等边三角形是三条边相等的三角形,等腰三角形是两条腰相等的三角形,所以等腰三角形的范围大于等边三角形的范围,等边三角形是特殊的等腰三角形,等腰三角形是特殊的三角形,故包含关系错误;
C.等腰三角形和等边三角形都属于三角形,但两者不是独立的,等边三角形是特殊的等腰三角形,故包含关系错误。
故答案为:A
【点睛】本题考查了三角形的分类,找清楚分类的标准,以及弄清楚它们之间的包含关系是解决本题的关键。
3.B
【分析】根据等边三角形的特性判定即可。
【详解】据等边三角形的特性可知:
三个角都是60°的三角形是等边三角形。
故答案为:B
【点睛】本题考查等边三角形的判定,解题的关键是掌握基本知识。
4.C
【分析】等腰三角形的两条腰相等。三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3cm、4cm、5cm,这三根小棒的长度都不相等,不能拼成等腰三角形。
B.3cm+3cm<7cm,长3cm、7cm、3cm的三根小棒不能拼成一个三角形。
C.5cm+5cm>6cm,长5cm、6cm、5cm的三根小棒能拼成一个三角形。且两根小棒长度相等,能拼成等腰三角形。
故答案为:C
【点睛】本题考查等腰三角形的特征以及三角形的三边关系,关键是熟练掌握三角形的三边关系是解题的关键。
5.C
【分析】根据题图可知,带第③块去最省事,因为它有一条完整的边和两个角,从而可以推算出三角形的另外一个角的度数及其它两边的长度,据此解答即可。
【详解】最省事的办法是带第③块去,因为它有一条完整的边和两个角;
故答案为:C。
【点睛】此题主要考查了三角形的内角和以及根据两个角和一条边确定另外两个边的知识。
6.50
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,因此用180°减去等腰三角形的顶角的度数后,再除以2即可,依此计算。
【详解】180°-80°=100°
100°÷2=50°
【点睛】熟记三角形的内角和度数与等腰三角形的特点是解答此题的关键。
7.19
【分析】根据任意两边之和大于第三边,知道等腰三角形的腰的长度是8厘米,底边长3厘米,据此解答即可。
【详解】因为3+3<8,所以等腰三角形的腰的长度是8厘米,底边长3厘米。
8+8+3
=16+3
=19(厘米)
【点睛】关键是先判断出三角形的两条腰的长度,问题即可得解。
8. 三角 平行四边
【分析】梯形是一个四边形,当梯形的上底缩短成一个点时,此时只有三个顶点,该图形由梯形转化为三角形;梯形的上底、下底互相平行,当上底增大到与下底相等时,一组对边平行且相等,此时梯形转化为平行四边形,据此解答。
【详解】
分析可知,当梯形的上底逐渐缩短到一个点时,梯形就转化成三角形,当梯形的上底增大到与下底相等时,梯形就转化成平行四边形。
【点睛】解题时通过画图分析,可以比较直观地看出图形的变化情况。
9. 直角 AB AC 38
【解析】略
10. 40 160
【分析】如下图,因为三角形内角和等于180°,∠1等于180°减去90°与50°的和;∠4等于180°减50°;∠3等于180°减∠4与30°的和;∠2等于180°减∠3,据此即可解答。
【详解】∠1=180°-(90°+50°)
=180°-140°
=40°
∠4=180°-50°=130°
∠3=180°-(∠4+30°)
=180°-(130°+30°)
=180°-160°
=20°
∠2=180°-∠3
=180°-20°
=160°
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
11.√
【分析】三角形具有稳定性的特征,生活中常常利用三角形这一特性对物体进行稳固,据此判断。
【详解】三角形具有稳定性,所以题目说法正确。
故答案为:√
【点睛】解决本题的关键是正确理解三角形的稳定性特征。
12.√
【分析】沿三角形的顶点做对边的高,通过直观图可以观察,任意一个三角形都可以分成两个直角三角形。
【详解】如图:
,原题说法正确。
故答案为:√
【点睛】解答此题的关键是从一个顶点作它对边的高进行判断。
13.√
【分析】等腰三角形的特点是两条腰相等,两个底角相等;等边三角形的特点是三条边都相等,三个角也相等;依此判断即可。
【详解】根据分析可知:等腰三角形和等边三角形的关系是。
故答案为:√
【点睛】熟练掌握等腰三角形和等边三角形的特点是解答此题的关键。
14.√
【分析】根据三角形的内角和为180°可知,最小的角是46°,其余两个角的度数和是180°-46°=134°。其中一个角应大于46°,最小是47°。则另一个角最大是134°-47°=87°。这三个角都是锐角,这个三角形是一个锐角三角形。
【详解】180°-46°=134°
134°-(46°+1°)
=134°-47°
=87°
则最小的角是46度,其余两个角最小是47度,最大是87°。三个角都是锐角,三角形是锐角三角形。
故答案为:√。
【点睛】本题考查三角形的内角和与三角形的分类,根据三角形的内角和判断其余两个角的度数取值范围,再进行判断。
15.×
【解析】略
16.70°;25°;52°
【分析】根据三角形的内角和是180°,求出∠1的度数,并由此求解。
【详解】据分析可知:
图1:180°-70°-90°
=110°-90°
=20°
∠1=90°-20°=70°
图2:∠1=180°-90°-65°
=90°-65°
=25°
图3:∠1=180°-60°-68°
=120°-68°
=52°
17.见详解
【分析】从与底边相对的顶点向底边作一条垂线,顶点和垂足之间的线段就是三角形的高。据此画图即可。画出高后标上垂直符号。
【详解】
【点睛】本题考查三角形高的画法,注意垂足所在的边叫做三角形的底。
18.第①条路,理由见解析
【分析】根据三角形的两边之和大于第三边或两点之间所有的连线中线段最短进行判断。
【详解】走第①条路最近。因为三角形的两边之和大于第三边(或两点之间线段最短)。
【点睛】本题考查三角形三边关系的应用,掌握三角形任意两条边的和大于第三边,两边之差小于第三边,是解题的关键。
19.15个
【分析】一个三角形地数有5个,两个三角形组成一个三角形有4个,三个三角形组成一个三角形有3个,四个三角形组成一个三角形有2个,五个三角形组成一个三角形有1个。
【详解】5+4+3+2+1
=9+3+2+1
=12+2+1
=14+1
=15(个)
答:图中一共有15个三角形。
【点睛】考查了组合图形中三角形的计数,注意按照一定的顺序数,做到不重复不遗漏。
20.14厘米
【分析】等腰三角形的两条腰相等。则这个等腰三角形的周长为12+12+18厘米。用同样的铁丝围成等边三角形,则这个等边三角形的周长也是12+12+18厘米。等边三角形的三条边相等,则边长=周长÷3,据此解答即可。
【详解】(12+12+18)÷3
=42÷3
=14(厘米)
答:等边三角形的边长是14厘米。
【点睛】等腰三角形的周长=2×腰+底,等边三角形的周长=3×边长。
21.88厘米
【分析】等腰三角形的两腰相等,因此用铁丝的总长度减去2个腰长即可,依此计算。
【详解】180-46×2
=180-92
=88(厘米)
答:底边长为88厘米。
【点睛】此题考查的是三角形的周长,熟练掌握等腰三角形的特点是解答此题的关键。
22.其他两个角都是;等腰三角形
【分析】最大角度数除以4等于最小角度数,再用180°减去最大角和最小角度数,就可求出第三个角的度数,再根据三角形的分类知识可知这块菜地是个什么三角形。
【详解】120°÷4=30°
180°-120°-30°
=60°-30°
=30°
由于三角形有两个角都是30°,所以这个菜地是个等腰三角形。
答:这块三角形蔬菜地其他两个角都是30度,是一个等腰三角形蔬菜地。
【点睛】本题主要考查学生对三角形内角和、三角形分类知识的掌握和灵活运用。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.下面各图中,给指定底边上的高画的正确的是( )。
A. B. C.
2.下面各图表示的关系正确的是( )。
A.B.C.
3.三个角都是60°的三角形是( )三角形。
A.锐角 B.等边 C.钝角
4.下面各组小棒中,能拼成等腰三角形的是( )。
A.3cm、4cm、5cm B.3cm、7cm、3cm C.5cm、6cm、5cm
5.下图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,最省事的办法是带第( )块去。
A.① B.② C.③
二、填空题
6.一个等腰三角形的顶角是80°,它的一个底角是( )度。
7.一个等腰三角形的一条边长是8厘米,另一条边长是3厘米,这个等腰三角形的周长是( )厘米。
8.当梯形的上底逐渐缩短到一个点时,梯形就转化成( )形,当梯形的上底增大到与下底相等时,梯形就转化成( )形。
9.如下图,三角形ABC是( )三角形,直角边BC对应的高是( ),BD是( )边对应的高。已知∠1=52°,那么∠2=( )°。
10.下图中的∠1=( )°,∠2=( )°。
三、判断题
11.高压电线杆上的支架做成三角形,是因为三角形具有稳定性。( )
12.任意一个三角形都可以分成两个直角三角形。( )
13.等腰三角形和等边三角形的关系是。( )
14.一个三角形中最小的角是46度,它一定是一个锐角三角形。( )
15.一个等腰三角形,其中两条边的长分别是8cm和4cm,则这个三角形的周长可能是20cm,也可能是16cm。( )
四、计算题
16.求出下面∠1的度数。
五、作图题
17.画出下面三角形指定底边上的高。
六、解答题
18.小熊要回家,走哪条路最近?为什么?
19.仔细观察下图,说一说图中一共有几个三角形?
20.一根铁丝可以围成一个腰长12厘米,底长18厘米的等腰三角形,如果改围一个等边三角形,那么等边三角形的边长是多少厘米?
21.某同学用一根180厘米长的铁丝围一个等腰三角形,经测量一条腰长为46厘米,底边长为多少厘米?
22.李爷爷有一块三角形蔬菜地,蔬菜地的最大角是,是最小角的4倍,这块三角形蔬菜地其他两个角各是多少度?按边分,这是一块什么三角形蔬菜地?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;从平行四边形或者梯形中互相平行的一组对边中的一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做它的高,垂足所在的边叫做底,据此解答。
【详解】由分析得,
A.底和高不是对应的,此题错误;
B.高不是垂直线段,此题错误;
C.底和高是对应的,此题正确。
故选:C
【点睛】此题考查的是平面图形的高的画法,解答此题应注意底和高必须是对应的。
2.A
【分析】根据三角形、等腰三角形和等边三角形的含义可知:等边三角形是特殊的等腰三角形,等腰三角形是特殊的三角形;由此解答即可。
【详解】A.三角形按边可以分为:不等边的三角形和等腰三角形,而等边三角形是特殊的等腰三角形,即等腰三角形包含了等边三角形,故包含关系正确;
B.等边三角形是三条边相等的三角形,等腰三角形是两条腰相等的三角形,所以等腰三角形的范围大于等边三角形的范围,等边三角形是特殊的等腰三角形,等腰三角形是特殊的三角形,故包含关系错误;
C.等腰三角形和等边三角形都属于三角形,但两者不是独立的,等边三角形是特殊的等腰三角形,故包含关系错误。
故答案为:A
【点睛】本题考查了三角形的分类,找清楚分类的标准,以及弄清楚它们之间的包含关系是解决本题的关键。
3.B
【分析】根据等边三角形的特性判定即可。
【详解】据等边三角形的特性可知:
三个角都是60°的三角形是等边三角形。
故答案为:B
【点睛】本题考查等边三角形的判定,解题的关键是掌握基本知识。
4.C
【分析】等腰三角形的两条腰相等。三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3cm、4cm、5cm,这三根小棒的长度都不相等,不能拼成等腰三角形。
B.3cm+3cm<7cm,长3cm、7cm、3cm的三根小棒不能拼成一个三角形。
C.5cm+5cm>6cm,长5cm、6cm、5cm的三根小棒能拼成一个三角形。且两根小棒长度相等,能拼成等腰三角形。
故答案为:C
【点睛】本题考查等腰三角形的特征以及三角形的三边关系,关键是熟练掌握三角形的三边关系是解题的关键。
5.C
【分析】根据题图可知,带第③块去最省事,因为它有一条完整的边和两个角,从而可以推算出三角形的另外一个角的度数及其它两边的长度,据此解答即可。
【详解】最省事的办法是带第③块去,因为它有一条完整的边和两个角;
故答案为:C。
【点睛】此题主要考查了三角形的内角和以及根据两个角和一条边确定另外两个边的知识。
6.50
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,因此用180°减去等腰三角形的顶角的度数后,再除以2即可,依此计算。
【详解】180°-80°=100°
100°÷2=50°
【点睛】熟记三角形的内角和度数与等腰三角形的特点是解答此题的关键。
7.19
【分析】根据任意两边之和大于第三边,知道等腰三角形的腰的长度是8厘米,底边长3厘米,据此解答即可。
【详解】因为3+3<8,所以等腰三角形的腰的长度是8厘米,底边长3厘米。
8+8+3
=16+3
=19(厘米)
【点睛】关键是先判断出三角形的两条腰的长度,问题即可得解。
8. 三角 平行四边
【分析】梯形是一个四边形,当梯形的上底缩短成一个点时,此时只有三个顶点,该图形由梯形转化为三角形;梯形的上底、下底互相平行,当上底增大到与下底相等时,一组对边平行且相等,此时梯形转化为平行四边形,据此解答。
【详解】
分析可知,当梯形的上底逐渐缩短到一个点时,梯形就转化成三角形,当梯形的上底增大到与下底相等时,梯形就转化成平行四边形。
【点睛】解题时通过画图分析,可以比较直观地看出图形的变化情况。
9. 直角 AB AC 38
【解析】略
10. 40 160
【分析】如下图,因为三角形内角和等于180°,∠1等于180°减去90°与50°的和;∠4等于180°减50°;∠3等于180°减∠4与30°的和;∠2等于180°减∠3,据此即可解答。
【详解】∠1=180°-(90°+50°)
=180°-140°
=40°
∠4=180°-50°=130°
∠3=180°-(∠4+30°)
=180°-(130°+30°)
=180°-160°
=20°
∠2=180°-∠3
=180°-20°
=160°
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
11.√
【分析】三角形具有稳定性的特征,生活中常常利用三角形这一特性对物体进行稳固,据此判断。
【详解】三角形具有稳定性,所以题目说法正确。
故答案为:√
【点睛】解决本题的关键是正确理解三角形的稳定性特征。
12.√
【分析】沿三角形的顶点做对边的高,通过直观图可以观察,任意一个三角形都可以分成两个直角三角形。
【详解】如图:
,原题说法正确。
故答案为:√
【点睛】解答此题的关键是从一个顶点作它对边的高进行判断。
13.√
【分析】等腰三角形的特点是两条腰相等,两个底角相等;等边三角形的特点是三条边都相等,三个角也相等;依此判断即可。
【详解】根据分析可知:等腰三角形和等边三角形的关系是。
故答案为:√
【点睛】熟练掌握等腰三角形和等边三角形的特点是解答此题的关键。
14.√
【分析】根据三角形的内角和为180°可知,最小的角是46°,其余两个角的度数和是180°-46°=134°。其中一个角应大于46°,最小是47°。则另一个角最大是134°-47°=87°。这三个角都是锐角,这个三角形是一个锐角三角形。
【详解】180°-46°=134°
134°-(46°+1°)
=134°-47°
=87°
则最小的角是46度,其余两个角最小是47度,最大是87°。三个角都是锐角,三角形是锐角三角形。
故答案为:√。
【点睛】本题考查三角形的内角和与三角形的分类,根据三角形的内角和判断其余两个角的度数取值范围,再进行判断。
15.×
【解析】略
16.70°;25°;52°
【分析】根据三角形的内角和是180°,求出∠1的度数,并由此求解。
【详解】据分析可知:
图1:180°-70°-90°
=110°-90°
=20°
∠1=90°-20°=70°
图2:∠1=180°-90°-65°
=90°-65°
=25°
图3:∠1=180°-60°-68°
=120°-68°
=52°
17.见详解
【分析】从与底边相对的顶点向底边作一条垂线,顶点和垂足之间的线段就是三角形的高。据此画图即可。画出高后标上垂直符号。
【详解】
【点睛】本题考查三角形高的画法,注意垂足所在的边叫做三角形的底。
18.第①条路,理由见解析
【分析】根据三角形的两边之和大于第三边或两点之间所有的连线中线段最短进行判断。
【详解】走第①条路最近。因为三角形的两边之和大于第三边(或两点之间线段最短)。
【点睛】本题考查三角形三边关系的应用,掌握三角形任意两条边的和大于第三边,两边之差小于第三边,是解题的关键。
19.15个
【分析】一个三角形地数有5个,两个三角形组成一个三角形有4个,三个三角形组成一个三角形有3个,四个三角形组成一个三角形有2个,五个三角形组成一个三角形有1个。
【详解】5+4+3+2+1
=9+3+2+1
=12+2+1
=14+1
=15(个)
答:图中一共有15个三角形。
【点睛】考查了组合图形中三角形的计数,注意按照一定的顺序数,做到不重复不遗漏。
20.14厘米
【分析】等腰三角形的两条腰相等。则这个等腰三角形的周长为12+12+18厘米。用同样的铁丝围成等边三角形,则这个等边三角形的周长也是12+12+18厘米。等边三角形的三条边相等,则边长=周长÷3,据此解答即可。
【详解】(12+12+18)÷3
=42÷3
=14(厘米)
答:等边三角形的边长是14厘米。
【点睛】等腰三角形的周长=2×腰+底,等边三角形的周长=3×边长。
21.88厘米
【分析】等腰三角形的两腰相等,因此用铁丝的总长度减去2个腰长即可,依此计算。
【详解】180-46×2
=180-92
=88(厘米)
答:底边长为88厘米。
【点睛】此题考查的是三角形的周长,熟练掌握等腰三角形的特点是解答此题的关键。
22.其他两个角都是;等腰三角形
【分析】最大角度数除以4等于最小角度数,再用180°减去最大角和最小角度数,就可求出第三个角的度数,再根据三角形的分类知识可知这块菜地是个什么三角形。
【详解】120°÷4=30°
180°-120°-30°
=60°-30°
=30°
由于三角形有两个角都是30°,所以这个菜地是个等腰三角形。
答:这块三角形蔬菜地其他两个角都是30度,是一个等腰三角形蔬菜地。
【点睛】本题主要考查学生对三角形内角和、三角形分类知识的掌握和灵活运用。
答案第1页,共2页
答案第1页,共2页
