10.3频率与概率 同步练习(含解析)2023——2024学年高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 10.3频率与概率 同步练习(含解析)2023——2024学年高中数学人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 00:00:00 | ||
图片预览




文档简介
10.3频率与概率 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛一枚硬币的试验中,下列对“伯努利大数定律”的理解正确的是( )
A.大量的试验中,出现正面的频率为0.5.
B.不管试验多少次,出现正面的概率始终为0.5
C.试验次数增大,出现正面的经验概率为0.5
D.试验次数每增加一次,下一次出现正面的频率一定比它前一次更接近于0.5
2.敏感性问题多属个人隐私.对敏感性问题的调查方案,关键是要使被调查者愿意作出真实回答又能保守个人秘密.例如为了调查中学生中的早恋现象,现有如下调查方案:在某校某年级,被调查者在没有旁人的情况下,独自一人回答问题.被调查者从一个罐子中随机抽一只球,看过颜色后即放回,若抽到白球,则回答问题A;若抽到红球,则回答问题B.且罐中只有白球和红球.
问题A:你的生日是否在7月1日之前 (本次调查中假设生日在7月1日之前的概率为)
问题B:你是否有早恋现象?
已知一次实际调查中,罐中放有白球2个,红球3个,调查结束后共收到1585张有效答卷,其中有393张回答“是”,如果以频率替代概率,则该校该年级学生有早恋现象的概率是( )(精确到0.01)
A.0.08 B.0.07 C.0.06 D.0.05
3.甲同学在数学探究活动中做抛硬币实验,共抛掷了2000次,其中正面朝上的有1034次,则下列说法正确的是( )
A.抛掷一枚硬币,正面朝上的概率为0.517
B.甲同学的实验中,反面朝上的频率为0.483
C.抛掷一枚硬币,反面朝上的概率小于0.5
D.甲同学的实验中,正面朝上的频率接近0.517
4.下列结论:①如果,那么为必然事件:
②若事件与是互斥事件,则;
③概率是随机的,试验前不能确定;
④若事件与是对立事件,则与一定是互斥事件.
其中是正确的个数是( )
A.1 B.2 C.3 D.4
5.下列说法中,正确的是( )
A.某种彩票中奖的概率是,因此买100张该种彩票一定会中奖
B.做7次拋硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
C.若事件两两互斥,则
D.任意投掷两枚质地均匀的骰子,则点数和是3的倍数的概率是
6.某学校在高三年级中抽取200名学生,调查他们课后完成作业的时间,并根据调查结果绘制了如下频率分布直方图.根据此直方图得出了下列结论,其中不正确的是( )
A.所抽取的学生中有40人在2.5小时至3小时之间完成作业
B.该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为0.1
C.估计该校高三年级学生的平均做作业的时间超过3小时
D.估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间
7.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )
A. B. C. D.
8.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 11 10 5 8 5 12 19 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.51 C.0.49 D.0.47
二、多选题
9.某校高三年级有(1),(2),(3)三个班,一次期末考试,统计得到每班学生的数学成绩的优秀率(数学成绩在120分以上的学生人数与该班学生总人数之比)如表所示:
班级 (1) (2) (3)
优秀率 80% 85% 75%
则下列说法一定正确的是( )
A.(2)班学生的数学成绩的优秀率最高
B.(3)班的学生人数不一定最少
C.该年级全体学生数学成绩的优秀率为80%
D.若把(1)班和(2)班的数学成绩放在一起统计,得到优秀率为83%,则(1)班人数多于(2)班人数
10.下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
C.随机事件发生的频率就是这个随机事件发生的概率
D.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
11.一座对外封闭的小岛上共有三座城市,三座城市第年居住人口分别为(单位万人,因为统计方法的影响,可能不为整数或有理数),假设出生率与死亡率相当(即总人口不变),每年人口都会在三座城市间流动,如城每年有留在城,有去往城,有去往城,总体流动情况如下表所示:
城市 每年去往 每年去往 每年去往
则以下说法中,正确的有( )
A.若,则
B.若三座城市人口均保持每年稳定不变,则
C.无论初始人口如何分布,经过足够久的年份后,三座城市的人口数会趋向相同
D.每两年的人口流动情况为下表所示:
城市 每两年去往 每两年去往 每两年去往
12.高中某学校对一次高三联考物理成绩进行统计分析,随机抽取100名学生成绩得到如图所示的频率分布直方图,其中分组的区间为,同时计划从样本中随机抽取个体进行随访,若从样本随机抽取个体互不影响,把频率视为概率,则下列结论正确的是( )
A.学生成绩众数估计为75分
B.考生成绩的第75百分位成绩估计为80分
C.在内随机抽取一名学生访谈,则甲被抽取的概率为0.01
D.从和内各抽1名学生,抽2名学生调研,又从他们中任取2人进行评估测试,则这2人来自不同组的概率为0.13
三、填空题
13.为研究吸烟是否与患肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法调查了人,已知非吸烟者占比,吸烟者中患肺癌的有人,根据统计结果表明,吸烟者患肺癌的概率是未吸烟者患肺癌的概率的倍,则估计本次研究调查中非吸烟者患肺癌的人数是 .
14.在一个不透明的纸盒中装有4个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.8附近,则袋子中红球约有 个.
15.在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如下的样本数据的频率分布直方图,由此可估计该地区一位这种疾病患者的年龄位于区间的概率为 .
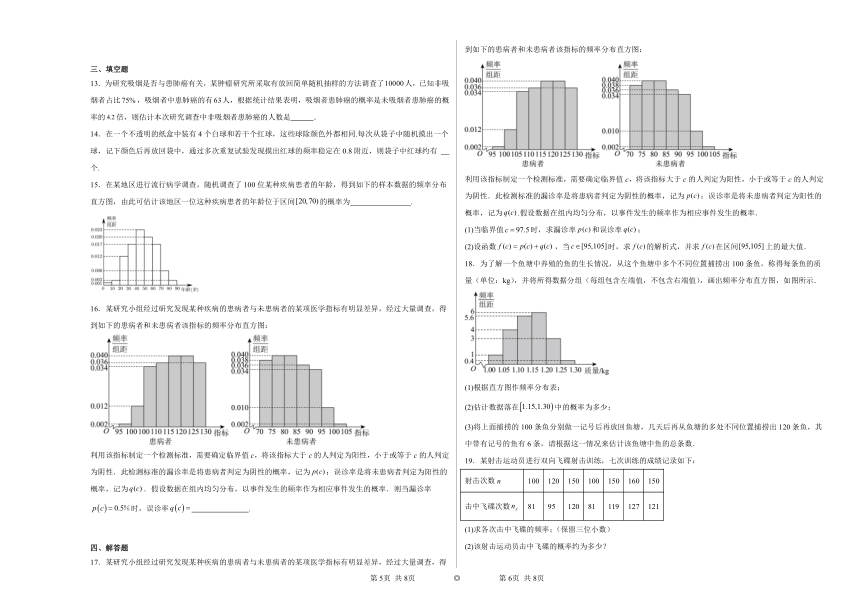
16.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.则当漏诊率时,误诊率 .
四、解答题
17.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)当临界值时,求漏诊率和误诊率;
(2)设函数,当时,求的解析式,并求在区间上的最大值.
18.为了解一个鱼塘中养殖的鱼的生长情况,从这个鱼塘中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组(每组包含左端值,不包含右端值),画出频率分布直方图,如图所示.
(1)根据直方图作频率分布表;
(2)估计数据落在中的概率为多少;
(3)将上面捕捞的100条鱼分别做一记号后再放回鱼塘,几天后再从鱼塘的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该鱼塘中鱼的总条数.
19.某射击运动员进行双向飞碟射击训练,七次训练的成绩记录如下:
射击次数n 100 120 150 100 150 160 150
击中飞碟次数 81 95 120 81 119 127 121
(1)求各次击中飞碟的频率;(保留三位小数)
(2)该射击运动员击中飞碟的概率约为多少?
20.目前,随着人们的生活节奏的加快,人们出行时乘坐的交通工具也逐渐多样化.某公司为了了解员工上个月上、下班时两种交通工具乘坐情况,从全公司所有的名员工中随机抽取了人,发现样本中两种交通工具都不乘坐的有人,样本中仅乘坐和仅乘坐的员工月交通费用分布情况如下:
交通费用交通工具 不大于元 大于元
仅乘坐 人 人
仅乘坐 人 人
(1)估计该公司员工中上个月两种交通工具都乘坐的人数;
(2)从样本中仅乘坐的员工中随机抽取人,求该员工上个月交通费用大于元的概率;
(3)已知上个月样本中的员工乘坐交通工具方式在本月没有变化.现从样本中仅乘坐的员工中随机抽查人,发现他本月交通费用大于元.结合(2)的结果,能否认为样本中仅乘坐的员工中本月交通费用大于元的人数有变化?请说明理由.
21.甲 乙两人准备参加某电视台举办的地理知识抢答赛.比赛规则为:每轮比赛每人随机在题库中抽取一道题作答,答对得1分,答错或不答得0分,最后得分多的获胜.为了在比赛中取得比较好的成绩,甲 乙两人在比赛前进行了针对性训练,训练后的答题情况如下表:
甲 乙
练习题目个数 120 120
答错个数 24 20
若比赛中每个人回答正确与否相互之间没有影响,且用频率代替概率.
(1)估计甲 乙两人在比赛时答对题的概率;
(2)设事件“某轮比赛中甲得1分或乙得1分”,求.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据频率、概率、经验概率的概念分析可得答案.
【详解】对于A,大量的试验中,出现正面的频率越来越接近于0.5,故A不正确;
对于B,事件发生的概率是一个常数,与试验次数无关,所以不管试验多少次,出现正面的概率始终为0.5,故B正确;
对于C,经验概率是指特定的事件发生的次数占总体试验样本的比率,随着试验次数增大,出现正面的经验概率约为0.5,故C不正确;
对于D,试验次数每增加一次,不能判断下一次出现正面的频率比它前一次更接近于0.5,D不正确.
故选:B
2.A
【分析】根据古典概型分别求出抽到红球的概率和抽到白球的概率,并且计算出回答问题A、B的人数,从而可分别计算出回答问题A、B的人中答 “是” 的人数以及比例.
【详解】从罐子中随机抽一个球, 抽到红球的概率为,
抽到白球的概率为,
所以回答问题A的人数是人
回答问题B的人数是人,
回答问题A的人中答 “是” 的人数是,
所以回答问题B的人中答 “是” 的人数是,
则估计该校该年级学生有早恋现象的概率为,
故选:A
3.B
【分析】根据概率与频率的关系判断.
【详解】甲同学的实验中,正面朝上的频率为0.517,反面朝上的频率为0.483,故B正确;
抛掷一枚硬币,正面朝上与反面朝上的概率均为0.5,为定值,故AC错误;
甲同学的实验中,正面朝上的频率就是0.517,而不是接近0.517,故D错误.
故选:B
4.A
【分析】根据必然事件、互斥事件、对立事件、概率等知识确定正确答案.
【详解】必然事件的概率是,所以①错误.
若事件与是互斥事件,则,所以②错误.
概率是理论值,是固定值,与实验前后无关,所以③错误.
若事件与是对立事件,则与一定是互斥事件,所以④正确.
所以正确的有个.
故选:A
5.D
【分析】根据随机事件的概念即可说明A、B;举例即可说明C项;列举出事件包含的样本点的个数,根据古典概型的概率公式,计算即可得出D项.
【详解】对于A项,由于事件结果的随机性,购买100张彩票不一定会中奖,故A错误;
对于B项,做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,故B错误;
对于C项,事件两两互斥,比如投掷质地均匀的骰子试验中,三个事件:投掷出1点,2点,3点,这三个事件两两互斥,但这三个事件的和事件发生的概率为,故C错误;
对于D项,任意投掷两枚质地均匀的骰子共包含36个等可能的样本点,
其中点数和是3的倍数的情况有,共12个样本点,
根据古典概型的概率公式,可得概率是,故D正确.
故选:D.
6.C
【分析】根据频率分布直方图结合统计、概率相关知识逐项分析判断.
【详解】对于A,在2.5小时至3小时之间的人数为人,故A正确;
对于B,该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为,故B正确;
对于C,该校高三年级学生的平均做作业的时间为
,
故C不正确;
对于D,由图可估计该校高三年级学生做作业的时间在2.5小时至4.5小时之间的频率为,
估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间,故D正确.
故选:C.
7.B
【分析】查出20个随机数中表示今后3天中恰有2天发布高温橙色预警信号的随机数的个数,根据古典概型的概率公式,即可求得答案.
【详解】由题意可知表示今后的3天中恰有2天发布高温橙色预警信号的随机数有:
116 812 730 217 109 361 284 147 318 027共10个,
故今后的3天中恰有2天发布高温橙色预警信号的概率估计是,
故选:B
8.B
【分析】运用频率定义计算即可.
【详解】由题意知,取到号码为奇数的频率为.
故选:B.
9.AB
【分析】由题目表格中的数据,逐一判断选项,可得答案.
【详解】选项A:显然(2)班学生的数学成绩的优秀率最高,故A正确;
选项B:只根据优秀率的大小,无法比较每个班人数的多少,故B正确;
选项C:该年级全体学生数学成绩的优秀率为全年级数学成绩优秀的学生人数与全年级学生总人数之比,
由于各班的学生人数不知道,所以不能计算该年级全体学生数学成绩的优秀率,故C错误;
选项D:设(1)班、(2)班数学成绩优秀的人数分别为x,y,(1)班、(2)班人数分别为a,b,
则,,得,,又(1)班和(2)班放在一起统计的优秀率为83%,
即,即,即,得,则,故D错误.
故选:AB.
10.ABC
【分析】
根据频率与概率的关系,结合各选项的描述判断正误.
【详解】对于A: 从中任取100件,可能有10件,A错误;
对于B: 做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,B错误;
对于C:多次重复试验中事件发生的频率在某一常数附近,此常数为概率,与描述不符,C错误;
对于D:10000次的界定没有科学依据,“不一定很准确"的表达正确,试验次数越多,频率越稳定在概率值附近,但并非试验次数越多,频率就等于概率,D正确.
故选: ABC.
11.BCD
【分析】由题意知,与满足的关系式,逐项计算即可得出答案.
【详解】由题意知与满足关系式:,其中,
对于A,当,
则,则,故A错误;
对于B,在上述关系式中令,反解线性方程组,
即可知恒成立,从而,故B正确;
对于C,由流动比例的轮换对称性及总人口不变,知三座城市人口趋于相同,故C正确;
对于D,将代入,
则,故D正确.
故选:BCD.
12.AB
【分析】根据频率分布直方图估计出众数,第75百分位数可判断AB;利用频率估计概率,古典概型等知识可判断CD.
【详解】由频率分布直方图得,成绩在的频率最高,所以估计成绩的众数为75分,故A正确;
因为,所以估计第75百分位成绩为80分,故B正确;
因为成绩在内的人数为,所以随机抽取一名学生访谈,甲被抽取的概率为,故C错误;
记从抽取的1名学生为a,从抽取的1名学生为b,从抽取的2名学生为c,d,则从这4人中抽取2人,所有的可能结果为
ab,ac,ad,bc,bd,cd,共6种,
其中不同组的有ab,ac,ad,bc,bd,共5种,
所以这2人来自不同组的概率为,故D错误;
故选:AB.
13.
【分析】设非吸烟者患肺癌的概率为,根据题意列出方程,求出,即可得到答案
【详解】本次研究调查中,非吸烟者有7500人,吸烟者样本量有2500人,
设非吸烟者患肺癌的人数是人,则,,
因此,本次研究调查中非吸烟者患肺癌的人数为45人.
故答案为:.
14.16
【分析】设袋中红球有个,根据概率的概念列式求解即可.
【详解】设袋中红球有个,根据题意,得,解得:,
经检验:是分式方程的解,所以袋中红球有16个.
故答案为:16
15.
【分析】根据频率分布直方图计算出这种疾病患者的年龄位于不在区间频率,结合对立事件的概率公式得到概率.
【详解】设{一人患这种疾病的年龄在区间},
所以.
故答案为:
16.
【分析】先根据左边的频率分布直方图得到,再根据右边的频率分布直方图可得.
【详解】依题可知,左边图形第一个小矩形的面积为,所以,
所以,解得:,
由右边的频率分布直方图可得.
故答案为:
17.(1)0.5%,3.5%;
(2),0.07.
【分析】(1)根据题意,由第一个图求出的矩形面积,再根据第二个图求出的矩形面积即可解出.
(2)根据题意,确定分段点100,即可得出的解析式,再根据分段函数的最值求法即可解出.
【详解】(1)依题意,,
.
(2)当时,
,
当时,;
当时,
,
当时,,
所以,在区间上的最大值为0.07.
18.(1)答案见解析
(2)0.47
(3)2000
【分析】(1)根据小矩形面积为各组频率求出频率列表即可;
(2)数据落在中的概率即为之间矩形面积之和;
(3)根据分层抽样的比例关系即可得到答案.
【详解】(1)根据频率分布直方图可知,频率=组距(频率/组距),故可得下表
分组 频率
0.05
0.20
0.28
0.30
0.15
0.02
(2),所以数据落在中的概率约为0.47.
(3)设水库中鱼的总条数约为条,则,
即,所以水库中鱼的总条数约为2000条.
19.(1)0.810,0.792,0.800,0.810,0.793,0.794,0.807
(2)0.800
【分析】(1)根据射击次数及击中飞碟次数计算频率即可;
(2)根据频率与概率的关系可得解.
【详解】(1)根据表格中数据,击中飞碟的频率依次为
,
.
(2)由(1)可知该射击运动员在同一条件下击中飞碟的频率都在0.800附近摆动,
所以该运动员击中飞碟的概率约为0.800.
20.(1)人
(2)
(3)答案见解析
【分析】(1)根据样本数据可计算得到样本中两种交通工具都乘坐的员工数,用样本估计总体可得结果;
(2)根据古典概型概率公式直接求解即可;
(3)根据随机事件概率比较小的特点来进行分析作答即可.
【详解】(1)由题意知:样本中上个月仅乘坐的员工有人,仅乘坐的员工有人,两种交通工具都不乘坐的有人,
样本中两种交通工具都乘坐的员工有人,
用样本估计总体,该公司员工中上个月两种交通工具都乘坐的人数为人.
(2)记事件:从样本中仅乘坐的员工中随机抽取人,该员工上个月的交通费用大于元,则.
(3)由(2)知:;
答案一:可以认为有变化.理由如下:
比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月交通费用大于元的人数发生了变化,可以认为有变化.
答案二:无法确定有没有变化.理由如下:
事件是随机事件,比较小,一般不容易发生,但还是有可能发生的,无法确定有没有变化.
21.(1)甲 乙两人在比赛时答对题的概率分别为
(2)
【分析】(1)根据题中条件计算出频率,用频率代替概率即可;
(2)根据互斥事件的概率加法公式进行计算即可.
【详解】(1)由题意,可以估计甲在比赛时答对题的概率为:
,
乙在比赛时答对题的概率为:
.
(2)设事件“某轮比赛中甲得1分”,事件“某轮比赛中乙得1分”,
则事件,
所以.
(或).
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛一枚硬币的试验中,下列对“伯努利大数定律”的理解正确的是( )
A.大量的试验中,出现正面的频率为0.5.
B.不管试验多少次,出现正面的概率始终为0.5
C.试验次数增大,出现正面的经验概率为0.5
D.试验次数每增加一次,下一次出现正面的频率一定比它前一次更接近于0.5
2.敏感性问题多属个人隐私.对敏感性问题的调查方案,关键是要使被调查者愿意作出真实回答又能保守个人秘密.例如为了调查中学生中的早恋现象,现有如下调查方案:在某校某年级,被调查者在没有旁人的情况下,独自一人回答问题.被调查者从一个罐子中随机抽一只球,看过颜色后即放回,若抽到白球,则回答问题A;若抽到红球,则回答问题B.且罐中只有白球和红球.
问题A:你的生日是否在7月1日之前 (本次调查中假设生日在7月1日之前的概率为)
问题B:你是否有早恋现象?
已知一次实际调查中,罐中放有白球2个,红球3个,调查结束后共收到1585张有效答卷,其中有393张回答“是”,如果以频率替代概率,则该校该年级学生有早恋现象的概率是( )(精确到0.01)
A.0.08 B.0.07 C.0.06 D.0.05
3.甲同学在数学探究活动中做抛硬币实验,共抛掷了2000次,其中正面朝上的有1034次,则下列说法正确的是( )
A.抛掷一枚硬币,正面朝上的概率为0.517
B.甲同学的实验中,反面朝上的频率为0.483
C.抛掷一枚硬币,反面朝上的概率小于0.5
D.甲同学的实验中,正面朝上的频率接近0.517
4.下列结论:①如果,那么为必然事件:
②若事件与是互斥事件,则;
③概率是随机的,试验前不能确定;
④若事件与是对立事件,则与一定是互斥事件.
其中是正确的个数是( )
A.1 B.2 C.3 D.4
5.下列说法中,正确的是( )
A.某种彩票中奖的概率是,因此买100张该种彩票一定会中奖
B.做7次拋硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
C.若事件两两互斥,则
D.任意投掷两枚质地均匀的骰子,则点数和是3的倍数的概率是
6.某学校在高三年级中抽取200名学生,调查他们课后完成作业的时间,并根据调查结果绘制了如下频率分布直方图.根据此直方图得出了下列结论,其中不正确的是( )
A.所抽取的学生中有40人在2.5小时至3小时之间完成作业
B.该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为0.1
C.估计该校高三年级学生的平均做作业的时间超过3小时
D.估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间
7.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )
A. B. C. D.
8.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 11 10 5 8 5 12 19 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.51 C.0.49 D.0.47
二、多选题
9.某校高三年级有(1),(2),(3)三个班,一次期末考试,统计得到每班学生的数学成绩的优秀率(数学成绩在120分以上的学生人数与该班学生总人数之比)如表所示:
班级 (1) (2) (3)
优秀率 80% 85% 75%
则下列说法一定正确的是( )
A.(2)班学生的数学成绩的优秀率最高
B.(3)班的学生人数不一定最少
C.该年级全体学生数学成绩的优秀率为80%
D.若把(1)班和(2)班的数学成绩放在一起统计,得到优秀率为83%,则(1)班人数多于(2)班人数
10.下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
C.随机事件发生的频率就是这个随机事件发生的概率
D.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
11.一座对外封闭的小岛上共有三座城市,三座城市第年居住人口分别为(单位万人,因为统计方法的影响,可能不为整数或有理数),假设出生率与死亡率相当(即总人口不变),每年人口都会在三座城市间流动,如城每年有留在城,有去往城,有去往城,总体流动情况如下表所示:
城市 每年去往 每年去往 每年去往
则以下说法中,正确的有( )
A.若,则
B.若三座城市人口均保持每年稳定不变,则
C.无论初始人口如何分布,经过足够久的年份后,三座城市的人口数会趋向相同
D.每两年的人口流动情况为下表所示:
城市 每两年去往 每两年去往 每两年去往
12.高中某学校对一次高三联考物理成绩进行统计分析,随机抽取100名学生成绩得到如图所示的频率分布直方图,其中分组的区间为,同时计划从样本中随机抽取个体进行随访,若从样本随机抽取个体互不影响,把频率视为概率,则下列结论正确的是( )
A.学生成绩众数估计为75分
B.考生成绩的第75百分位成绩估计为80分
C.在内随机抽取一名学生访谈,则甲被抽取的概率为0.01
D.从和内各抽1名学生,抽2名学生调研,又从他们中任取2人进行评估测试,则这2人来自不同组的概率为0.13
三、填空题
13.为研究吸烟是否与患肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法调查了人,已知非吸烟者占比,吸烟者中患肺癌的有人,根据统计结果表明,吸烟者患肺癌的概率是未吸烟者患肺癌的概率的倍,则估计本次研究调查中非吸烟者患肺癌的人数是 .
14.在一个不透明的纸盒中装有4个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.8附近,则袋子中红球约有 个.
15.在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如下的样本数据的频率分布直方图,由此可估计该地区一位这种疾病患者的年龄位于区间的概率为 .
16.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.则当漏诊率时,误诊率 .
四、解答题
17.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)当临界值时,求漏诊率和误诊率;
(2)设函数,当时,求的解析式,并求在区间上的最大值.
18.为了解一个鱼塘中养殖的鱼的生长情况,从这个鱼塘中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组(每组包含左端值,不包含右端值),画出频率分布直方图,如图所示.
(1)根据直方图作频率分布表;
(2)估计数据落在中的概率为多少;
(3)将上面捕捞的100条鱼分别做一记号后再放回鱼塘,几天后再从鱼塘的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该鱼塘中鱼的总条数.
19.某射击运动员进行双向飞碟射击训练,七次训练的成绩记录如下:
射击次数n 100 120 150 100 150 160 150
击中飞碟次数 81 95 120 81 119 127 121
(1)求各次击中飞碟的频率;(保留三位小数)
(2)该射击运动员击中飞碟的概率约为多少?
20.目前,随着人们的生活节奏的加快,人们出行时乘坐的交通工具也逐渐多样化.某公司为了了解员工上个月上、下班时两种交通工具乘坐情况,从全公司所有的名员工中随机抽取了人,发现样本中两种交通工具都不乘坐的有人,样本中仅乘坐和仅乘坐的员工月交通费用分布情况如下:
交通费用交通工具 不大于元 大于元
仅乘坐 人 人
仅乘坐 人 人
(1)估计该公司员工中上个月两种交通工具都乘坐的人数;
(2)从样本中仅乘坐的员工中随机抽取人,求该员工上个月交通费用大于元的概率;
(3)已知上个月样本中的员工乘坐交通工具方式在本月没有变化.现从样本中仅乘坐的员工中随机抽查人,发现他本月交通费用大于元.结合(2)的结果,能否认为样本中仅乘坐的员工中本月交通费用大于元的人数有变化?请说明理由.
21.甲 乙两人准备参加某电视台举办的地理知识抢答赛.比赛规则为:每轮比赛每人随机在题库中抽取一道题作答,答对得1分,答错或不答得0分,最后得分多的获胜.为了在比赛中取得比较好的成绩,甲 乙两人在比赛前进行了针对性训练,训练后的答题情况如下表:
甲 乙
练习题目个数 120 120
答错个数 24 20
若比赛中每个人回答正确与否相互之间没有影响,且用频率代替概率.
(1)估计甲 乙两人在比赛时答对题的概率;
(2)设事件“某轮比赛中甲得1分或乙得1分”,求.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据频率、概率、经验概率的概念分析可得答案.
【详解】对于A,大量的试验中,出现正面的频率越来越接近于0.5,故A不正确;
对于B,事件发生的概率是一个常数,与试验次数无关,所以不管试验多少次,出现正面的概率始终为0.5,故B正确;
对于C,经验概率是指特定的事件发生的次数占总体试验样本的比率,随着试验次数增大,出现正面的经验概率约为0.5,故C不正确;
对于D,试验次数每增加一次,不能判断下一次出现正面的频率比它前一次更接近于0.5,D不正确.
故选:B
2.A
【分析】根据古典概型分别求出抽到红球的概率和抽到白球的概率,并且计算出回答问题A、B的人数,从而可分别计算出回答问题A、B的人中答 “是” 的人数以及比例.
【详解】从罐子中随机抽一个球, 抽到红球的概率为,
抽到白球的概率为,
所以回答问题A的人数是人
回答问题B的人数是人,
回答问题A的人中答 “是” 的人数是,
所以回答问题B的人中答 “是” 的人数是,
则估计该校该年级学生有早恋现象的概率为,
故选:A
3.B
【分析】根据概率与频率的关系判断.
【详解】甲同学的实验中,正面朝上的频率为0.517,反面朝上的频率为0.483,故B正确;
抛掷一枚硬币,正面朝上与反面朝上的概率均为0.5,为定值,故AC错误;
甲同学的实验中,正面朝上的频率就是0.517,而不是接近0.517,故D错误.
故选:B
4.A
【分析】根据必然事件、互斥事件、对立事件、概率等知识确定正确答案.
【详解】必然事件的概率是,所以①错误.
若事件与是互斥事件,则,所以②错误.
概率是理论值,是固定值,与实验前后无关,所以③错误.
若事件与是对立事件,则与一定是互斥事件,所以④正确.
所以正确的有个.
故选:A
5.D
【分析】根据随机事件的概念即可说明A、B;举例即可说明C项;列举出事件包含的样本点的个数,根据古典概型的概率公式,计算即可得出D项.
【详解】对于A项,由于事件结果的随机性,购买100张彩票不一定会中奖,故A错误;
对于B项,做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,故B错误;
对于C项,事件两两互斥,比如投掷质地均匀的骰子试验中,三个事件:投掷出1点,2点,3点,这三个事件两两互斥,但这三个事件的和事件发生的概率为,故C错误;
对于D项,任意投掷两枚质地均匀的骰子共包含36个等可能的样本点,
其中点数和是3的倍数的情况有,共12个样本点,
根据古典概型的概率公式,可得概率是,故D正确.
故选:D.
6.C
【分析】根据频率分布直方图结合统计、概率相关知识逐项分析判断.
【详解】对于A,在2.5小时至3小时之间的人数为人,故A正确;
对于B,该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为,故B正确;
对于C,该校高三年级学生的平均做作业的时间为
,
故C不正确;
对于D,由图可估计该校高三年级学生做作业的时间在2.5小时至4.5小时之间的频率为,
估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间,故D正确.
故选:C.
7.B
【分析】查出20个随机数中表示今后3天中恰有2天发布高温橙色预警信号的随机数的个数,根据古典概型的概率公式,即可求得答案.
【详解】由题意可知表示今后的3天中恰有2天发布高温橙色预警信号的随机数有:
116 812 730 217 109 361 284 147 318 027共10个,
故今后的3天中恰有2天发布高温橙色预警信号的概率估计是,
故选:B
8.B
【分析】运用频率定义计算即可.
【详解】由题意知,取到号码为奇数的频率为.
故选:B.
9.AB
【分析】由题目表格中的数据,逐一判断选项,可得答案.
【详解】选项A:显然(2)班学生的数学成绩的优秀率最高,故A正确;
选项B:只根据优秀率的大小,无法比较每个班人数的多少,故B正确;
选项C:该年级全体学生数学成绩的优秀率为全年级数学成绩优秀的学生人数与全年级学生总人数之比,
由于各班的学生人数不知道,所以不能计算该年级全体学生数学成绩的优秀率,故C错误;
选项D:设(1)班、(2)班数学成绩优秀的人数分别为x,y,(1)班、(2)班人数分别为a,b,
则,,得,,又(1)班和(2)班放在一起统计的优秀率为83%,
即,即,即,得,则,故D错误.
故选:AB.
10.ABC
【分析】
根据频率与概率的关系,结合各选项的描述判断正误.
【详解】对于A: 从中任取100件,可能有10件,A错误;
对于B: 做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,B错误;
对于C:多次重复试验中事件发生的频率在某一常数附近,此常数为概率,与描述不符,C错误;
对于D:10000次的界定没有科学依据,“不一定很准确"的表达正确,试验次数越多,频率越稳定在概率值附近,但并非试验次数越多,频率就等于概率,D正确.
故选: ABC.
11.BCD
【分析】由题意知,与满足的关系式,逐项计算即可得出答案.
【详解】由题意知与满足关系式:,其中,
对于A,当,
则,则,故A错误;
对于B,在上述关系式中令,反解线性方程组,
即可知恒成立,从而,故B正确;
对于C,由流动比例的轮换对称性及总人口不变,知三座城市人口趋于相同,故C正确;
对于D,将代入,
则,故D正确.
故选:BCD.
12.AB
【分析】根据频率分布直方图估计出众数,第75百分位数可判断AB;利用频率估计概率,古典概型等知识可判断CD.
【详解】由频率分布直方图得,成绩在的频率最高,所以估计成绩的众数为75分,故A正确;
因为,所以估计第75百分位成绩为80分,故B正确;
因为成绩在内的人数为,所以随机抽取一名学生访谈,甲被抽取的概率为,故C错误;
记从抽取的1名学生为a,从抽取的1名学生为b,从抽取的2名学生为c,d,则从这4人中抽取2人,所有的可能结果为
ab,ac,ad,bc,bd,cd,共6种,
其中不同组的有ab,ac,ad,bc,bd,共5种,
所以这2人来自不同组的概率为,故D错误;
故选:AB.
13.
【分析】设非吸烟者患肺癌的概率为,根据题意列出方程,求出,即可得到答案
【详解】本次研究调查中,非吸烟者有7500人,吸烟者样本量有2500人,
设非吸烟者患肺癌的人数是人,则,,
因此,本次研究调查中非吸烟者患肺癌的人数为45人.
故答案为:.
14.16
【分析】设袋中红球有个,根据概率的概念列式求解即可.
【详解】设袋中红球有个,根据题意,得,解得:,
经检验:是分式方程的解,所以袋中红球有16个.
故答案为:16
15.
【分析】根据频率分布直方图计算出这种疾病患者的年龄位于不在区间频率,结合对立事件的概率公式得到概率.
【详解】设{一人患这种疾病的年龄在区间},
所以.
故答案为:
16.
【分析】先根据左边的频率分布直方图得到,再根据右边的频率分布直方图可得.
【详解】依题可知,左边图形第一个小矩形的面积为,所以,
所以,解得:,
由右边的频率分布直方图可得.
故答案为:
17.(1)0.5%,3.5%;
(2),0.07.
【分析】(1)根据题意,由第一个图求出的矩形面积,再根据第二个图求出的矩形面积即可解出.
(2)根据题意,确定分段点100,即可得出的解析式,再根据分段函数的最值求法即可解出.
【详解】(1)依题意,,
.
(2)当时,
,
当时,;
当时,
,
当时,,
所以,在区间上的最大值为0.07.
18.(1)答案见解析
(2)0.47
(3)2000
【分析】(1)根据小矩形面积为各组频率求出频率列表即可;
(2)数据落在中的概率即为之间矩形面积之和;
(3)根据分层抽样的比例关系即可得到答案.
【详解】(1)根据频率分布直方图可知,频率=组距(频率/组距),故可得下表
分组 频率
0.05
0.20
0.28
0.30
0.15
0.02
(2),所以数据落在中的概率约为0.47.
(3)设水库中鱼的总条数约为条,则,
即,所以水库中鱼的总条数约为2000条.
19.(1)0.810,0.792,0.800,0.810,0.793,0.794,0.807
(2)0.800
【分析】(1)根据射击次数及击中飞碟次数计算频率即可;
(2)根据频率与概率的关系可得解.
【详解】(1)根据表格中数据,击中飞碟的频率依次为
,
.
(2)由(1)可知该射击运动员在同一条件下击中飞碟的频率都在0.800附近摆动,
所以该运动员击中飞碟的概率约为0.800.
20.(1)人
(2)
(3)答案见解析
【分析】(1)根据样本数据可计算得到样本中两种交通工具都乘坐的员工数,用样本估计总体可得结果;
(2)根据古典概型概率公式直接求解即可;
(3)根据随机事件概率比较小的特点来进行分析作答即可.
【详解】(1)由题意知:样本中上个月仅乘坐的员工有人,仅乘坐的员工有人,两种交通工具都不乘坐的有人,
样本中两种交通工具都乘坐的员工有人,
用样本估计总体,该公司员工中上个月两种交通工具都乘坐的人数为人.
(2)记事件:从样本中仅乘坐的员工中随机抽取人,该员工上个月的交通费用大于元,则.
(3)由(2)知:;
答案一:可以认为有变化.理由如下:
比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月交通费用大于元的人数发生了变化,可以认为有变化.
答案二:无法确定有没有变化.理由如下:
事件是随机事件,比较小,一般不容易发生,但还是有可能发生的,无法确定有没有变化.
21.(1)甲 乙两人在比赛时答对题的概率分别为
(2)
【分析】(1)根据题中条件计算出频率,用频率代替概率即可;
(2)根据互斥事件的概率加法公式进行计算即可.
【详解】(1)由题意,可以估计甲在比赛时答对题的概率为:
,
乙在比赛时答对题的概率为:
.
(2)设事件“某轮比赛中甲得1分”,事件“某轮比赛中乙得1分”,
则事件,
所以.
(或).
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
