北师大版八年级上册课件2.1 认识无理数
文档属性
| 名称 | 北师大版八年级上册课件2.1 认识无理数 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-13 00:00:00 | ||
图片预览





文档简介
课件27张PPT。1.认识无理数11(1)通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性.(2)学生经历数学思考与探索,进一步发展学生的抽象思维水平.(3)充分调动学生的积极性,培养学生的合作精神,提高辩识能力.1.知识目标2.教学重点
理解无理数包含的两个条件:无限性和不循环.3.教学难点
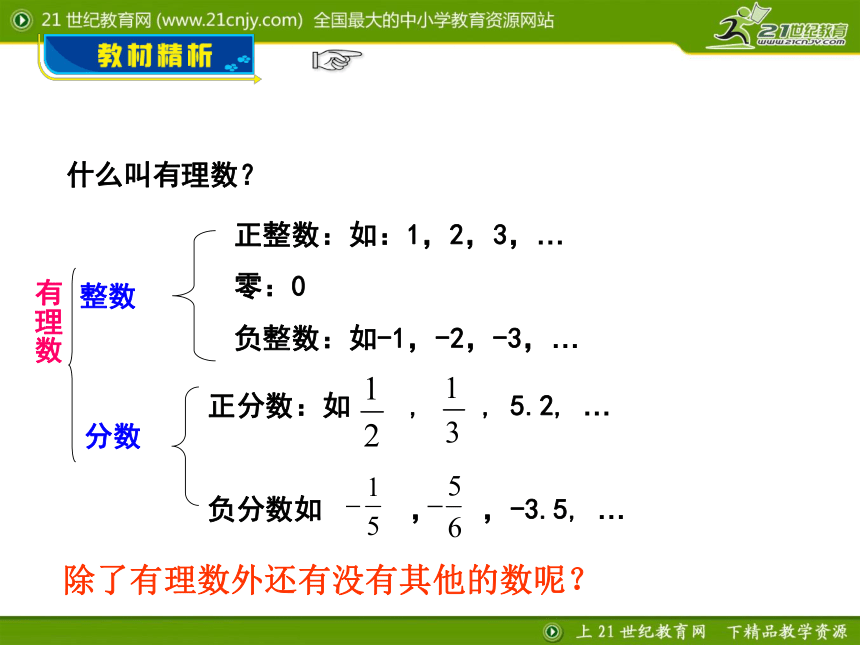
无理数存在的探索过程.整数正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…分数正分数:如 , , 5.2, …
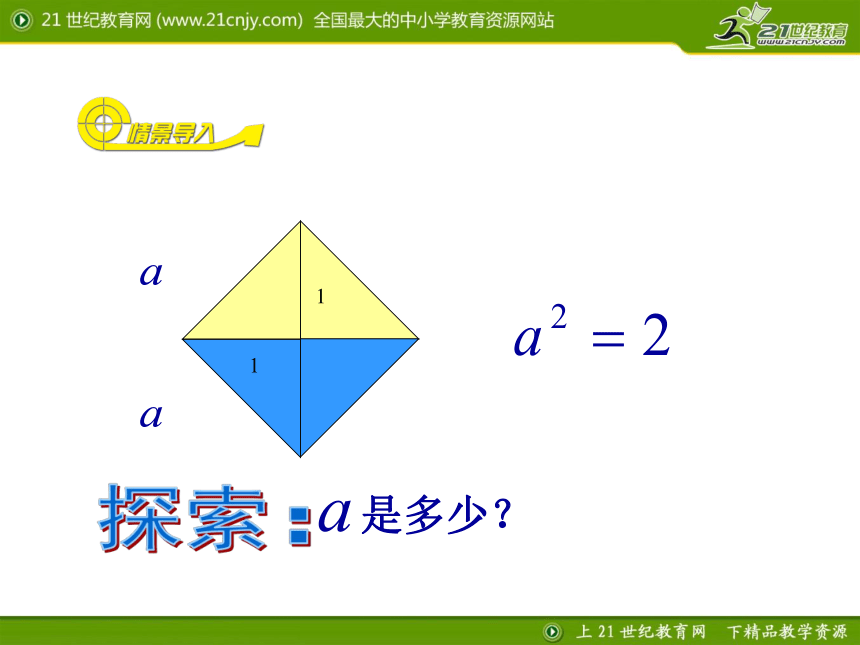
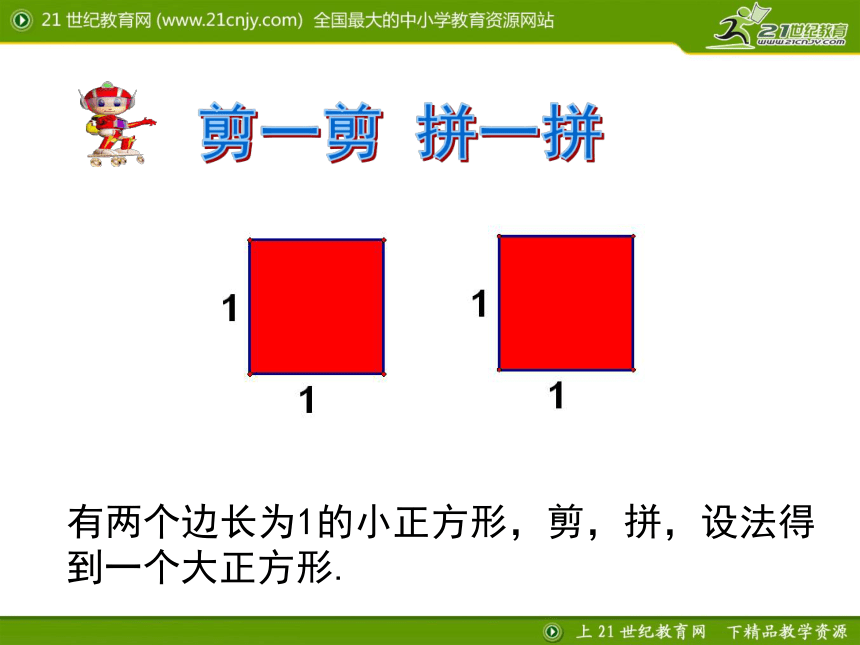
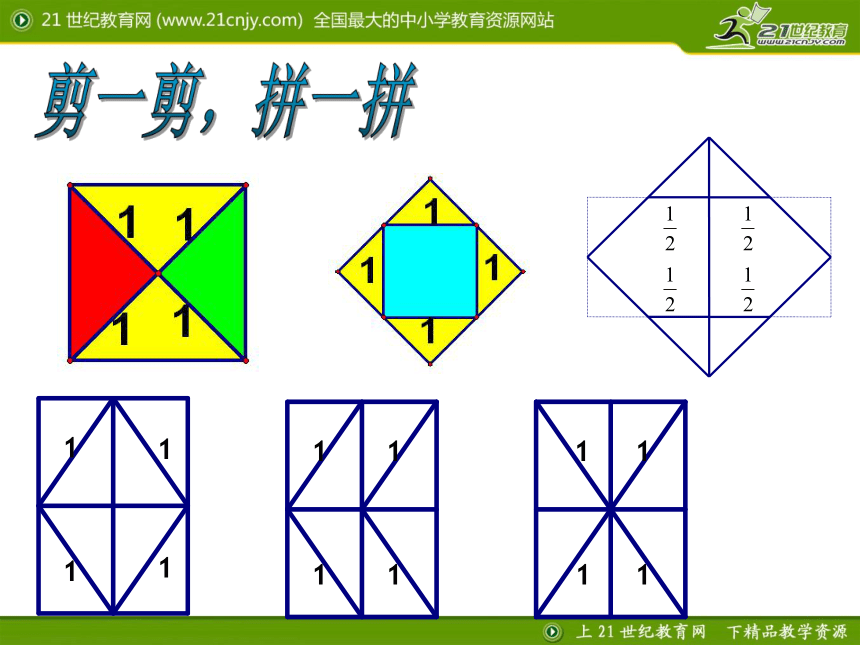
负分数如 , ,-3.5, …?什么叫有理数?除了有理数外还有没有其他的数呢?有两个边长为1的小正方形,剪,拼,设法得到一个大正方形.剪一剪 拼一拼剪一剪,拼一拼 (1)设大正方形的边长为a,
a满足什么条件?(3)a可能是分数吗?说说你的理由,并与同伴交流. (2) a可能是整数吗?说说你的理由.因为12=1,22=4,32=9,所以a不可能是整数a2 = 2议一议结论:在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数. a究竟是什么数?探索:思考:a究竟是什么数?像0.585 885 888 588 885…,1.414 213 56…,2.236 067 9…等这些数的小数位数都是无限的,但
是又不是循环的,是无限不循环小数,也叫无理数.(圆周率π=3.141 592 65…也是一个无限不循环小数,
故π是无理数)事实上,a=1.414 213 56…... c=2.236 067 978…… 它们是一个无限不循环小数.活动2:分数化成小数,最终此小数的形式有几种情况?请同学们以学习小组活动:一同学举出任意一分数,另一同学将此分数化成小数.并总结此小数的形式?结论:分数只能化成有限小数或无限循环小数.即任何有限小数或无限循环小数都是有理数.分一分到目前为止我们所学过的数可以分为几类?有理数:有限小数或无限循环小数无理数:无限不循环小数数整数分数例1 下列数哪些是有理数? 哪些是无理数?3.14159,-5.232 332…,123.345 678 910 11…(由相继的正整数组成).有理数无理数3.141 59,-5.232332…0.123 345 678 910 11………(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( ) 例2 判断题╳√√╳以下各正方形的边长是无理数的是( )C例3例4 一个直角三角形两条直角边的长分别是3和5,则斜边a是有理数吗?解:由勾股定理得:a2=32+52,即a2=34.因为34不是完全平方数,所以a不是有理数.
跟踪练习1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?h不可能是整数;h也不可能是分数. 2. B,C是一个生活小区的两个路口,BC长为2千米,A处是一个花园,从A到B,C两路口的距离都是2千米,现要从花园到生活小区修一条最短的路,这条路的长可能是整数吗?可能是分数吗?说明理由. 解:这条路的长既不是整数也不是分数,因为这个数的
平方等于3.
生活中真的有很多不是有理数的数吗? 右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.试分别找出两条长度是有理数的线段和两条长度不是有理数的线段.拔尖自助餐由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示. 例如: 线段AB,DE,AE的长
能用有理数表示;设计面积为5π的圆的半径为a.
(1)a是有理数吗?说说你的理由.
(2)估计a的值(精确到十分位,并利用你的计算器验证
你的估计.
(3)如果精确到百分位呢?课堂检测解:∵πa2=5π,∴ a2=5 .
(1)a不是有理数,因为a既不是整数,也不是分数,而是无限不循环小数.(2)估计a≈2.2.(3)估计a≈2.24.本节课你学到了什么?感悟与反思1.在生活中确实存在既不是整数也不是分数的数,既
不是有理数的数.2.无理数在现实生活中是大量存在的.祝同学们学习进步!再见!
理解无理数包含的两个条件:无限性和不循环.3.教学难点
无理数存在的探索过程.整数正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…分数正分数:如 , , 5.2, …
负分数如 , ,-3.5, …?什么叫有理数?除了有理数外还有没有其他的数呢?有两个边长为1的小正方形,剪,拼,设法得到一个大正方形.剪一剪 拼一拼剪一剪,拼一拼 (1)设大正方形的边长为a,
a满足什么条件?(3)a可能是分数吗?说说你的理由,并与同伴交流. (2) a可能是整数吗?说说你的理由.因为12=1,22=4,32=9,所以a不可能是整数a2 = 2议一议结论:在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数. a究竟是什么数?探索:思考:a究竟是什么数?像0.585 885 888 588 885…,1.414 213 56…,2.236 067 9…等这些数的小数位数都是无限的,但
是又不是循环的,是无限不循环小数,也叫无理数.(圆周率π=3.141 592 65…也是一个无限不循环小数,
故π是无理数)事实上,a=1.414 213 56…... c=2.236 067 978…… 它们是一个无限不循环小数.活动2:分数化成小数,最终此小数的形式有几种情况?请同学们以学习小组活动:一同学举出任意一分数,另一同学将此分数化成小数.并总结此小数的形式?结论:分数只能化成有限小数或无限循环小数.即任何有限小数或无限循环小数都是有理数.分一分到目前为止我们所学过的数可以分为几类?有理数:有限小数或无限循环小数无理数:无限不循环小数数整数分数例1 下列数哪些是有理数? 哪些是无理数?3.14159,-5.232 332…,123.345 678 910 11…(由相继的正整数组成).有理数无理数3.141 59,-5.232332…0.123 345 678 910 11………(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( ) 例2 判断题╳√√╳以下各正方形的边长是无理数的是( )C例3例4 一个直角三角形两条直角边的长分别是3和5,则斜边a是有理数吗?解:由勾股定理得:a2=32+52,即a2=34.因为34不是完全平方数,所以a不是有理数.
跟踪练习1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?h不可能是整数;h也不可能是分数. 2. B,C是一个生活小区的两个路口,BC长为2千米,A处是一个花园,从A到B,C两路口的距离都是2千米,现要从花园到生活小区修一条最短的路,这条路的长可能是整数吗?可能是分数吗?说明理由. 解:这条路的长既不是整数也不是分数,因为这个数的
平方等于3.
生活中真的有很多不是有理数的数吗? 右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.试分别找出两条长度是有理数的线段和两条长度不是有理数的线段.拔尖自助餐由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示. 例如: 线段AB,DE,AE的长
能用有理数表示;设计面积为5π的圆的半径为a.
(1)a是有理数吗?说说你的理由.
(2)估计a的值(精确到十分位,并利用你的计算器验证
你的估计.
(3)如果精确到百分位呢?课堂检测解:∵πa2=5π,∴ a2=5 .
(1)a不是有理数,因为a既不是整数,也不是分数,而是无限不循环小数.(2)估计a≈2.2.(3)估计a≈2.24.本节课你学到了什么?感悟与反思1.在生活中确实存在既不是整数也不是分数的数,既
不是有理数的数.2.无理数在现实生活中是大量存在的.祝同学们学习进步!再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
