北师大版八年级上册课件3.3 轴对称与坐标变化
文档属性
| 名称 | 北师大版八年级上册课件3.3 轴对称与坐标变化 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-13 00:00:00 | ||
图片预览



文档简介
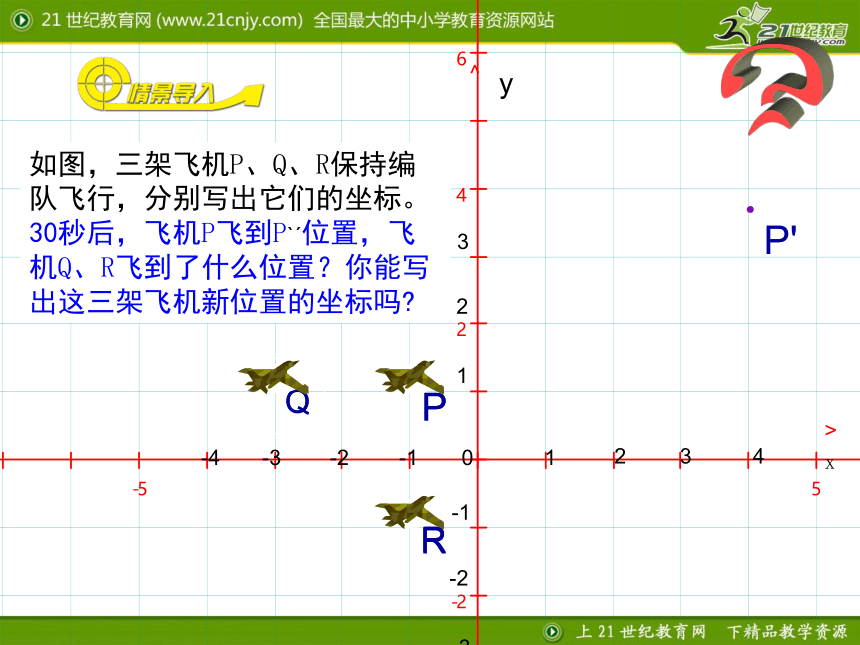
课件20张PPT。3 轴对称与坐标变化^y>x01123432-1-2-3-1-2-3-4?如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。 30秒后,飞机P飞到Pˋˊ位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗?1.知识目标
(1)认识图形的轴对称、中心对称变换与坐标变化之间的关系.
(2)以平面直角坐标系为工具体会数形结合.2.教学重点
点的坐标变化与图形变化之间的关系.3.教学难点
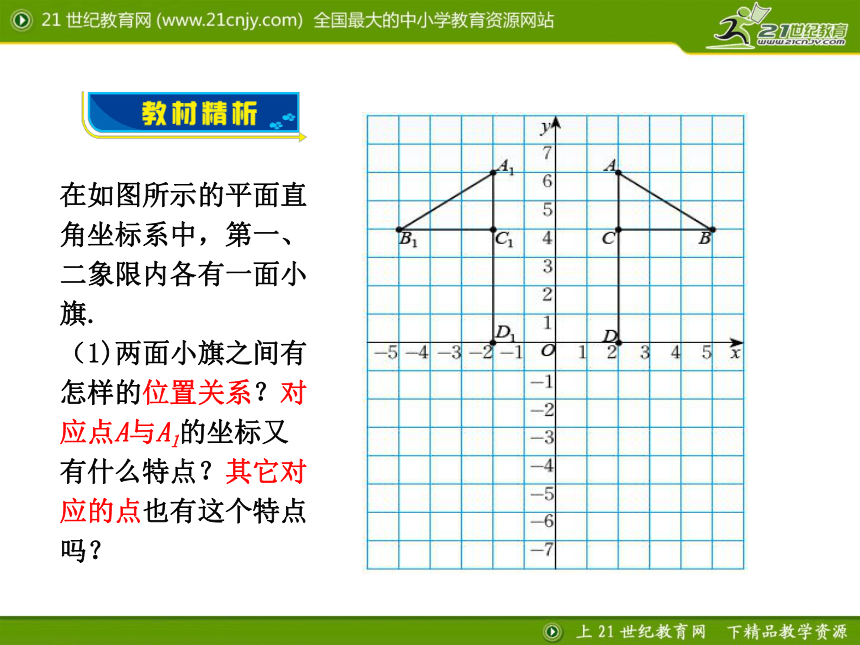
点坐标变化与图形变化之间的变化规律.在如图所示的平面直
角坐标系中,第一、
二象限内各有一面小
旗.
(1)两面小旗之间有
怎样的位置关系?对
应点A与A1的坐标又
有什么特点?其它对
应的点也有这个特点
吗?归纳 概括1.关于x轴对称的两点,它们的横坐标 ,
纵坐标 ;
2.关于y轴对称的两点,它们的横坐标 ,
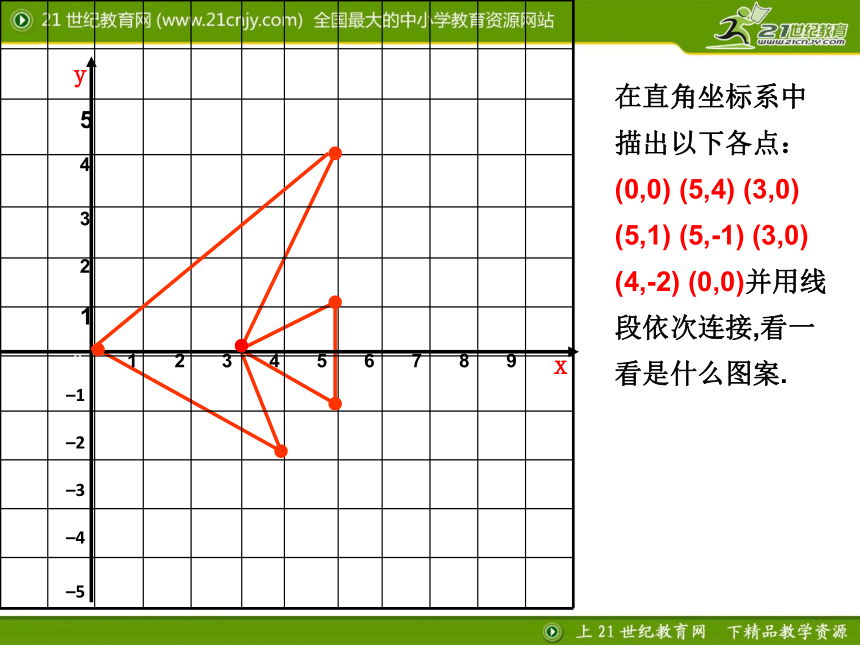
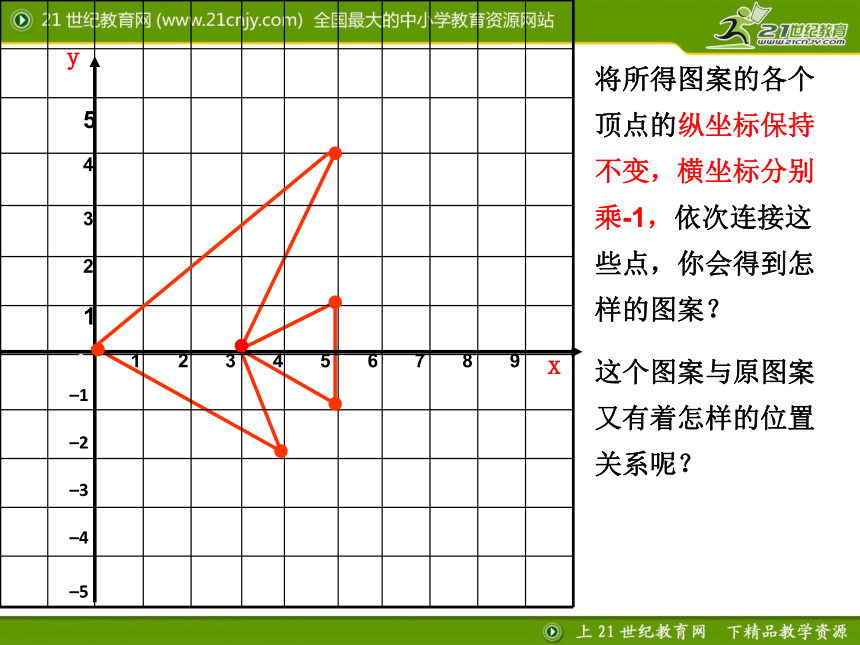
纵坐标 .相同互为相反数相同互为相反数在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案. yx将所得图案的各个顶点的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
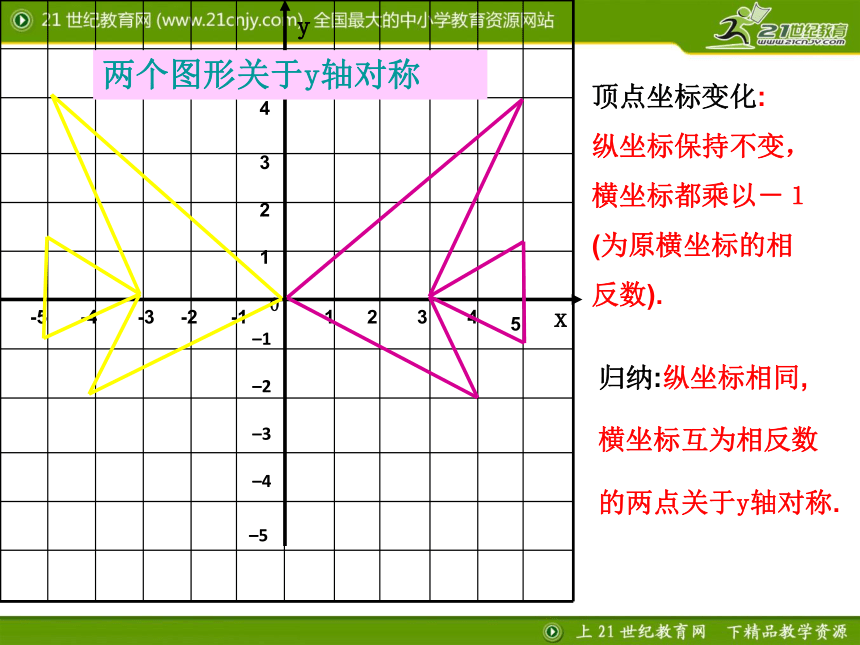
这个图案与原图案又有着怎样的位置关系呢? yx12345-1-2-30–1–2–3–4–51234-4-55yx两个图形关于y轴对称顶点坐标变化:
纵坐标保持不变,
横坐标都乘以-1
(为原横坐标的相
反数).归纳:纵坐标相同,
横坐标互为相反数
的两点关于y轴对称. 将各坐标的纵
坐标都乘以
-1,横坐标保
持不变,则图形
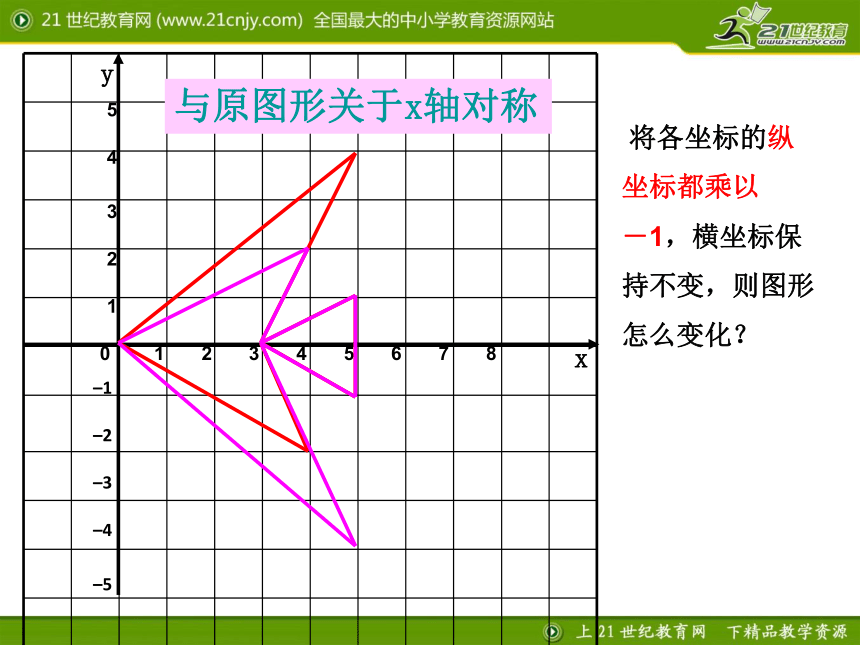
怎么变化?yx与原图形关于x轴对称 将各坐标的纵
坐标都乘以-1,
横坐标保持不
变,则图形怎么
变化?yx与原图形关于x轴对称归纳:横坐标相同,
纵坐标互为相反
数的两点关于x
轴对称.–5 将各坐标的纵坐标与横坐标都乘以-1,图形会变成什么样?yx与原图形关于原点中心对称归纳:
横,纵坐标都互
为相反数的两
点关于原点对称.例 已知△ABC 的三个顶点的坐标分别为A(-3,5),B(- 4,1),C (-1,3),作出△ABC 关于y 轴和x 轴对称的图形.····AB ′A ′C ′1.将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形( )
A. 关于X轴对称. B. 关于Y轴对称
C. 关于原点对称 D. 无法确定
2.点A(-3,2)与点B(-3,-2)的关系是( )
A.关于X轴对称 B.关于Y轴对称
C.关于原点对称 D.以上各项都不对
3.已知点M(3,-2),点N(a,b)是M点关于Y轴的对称点,则 a= , b= .
4.已知点P(a-1,5)和点Q(2,b-1)关于X轴对称,则
a= ,b= .A-3-23-4跟踪练习AA`(-4,-1) 如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于x轴和y 轴对称的图形.···C`(-3,-2)B`(-1,1)拔尖自助餐xy课堂检测1.已知点P(2a-3,4),点A(-1,2b+2),
(1)如果点P与点A关于x轴对称,那么a+b=___
(2)如果点P与点A关于y轴对称,那么a+b=___
2.已知A、B两点的坐标分别是(-2,3)和(2,3), 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( ) A.1个 B.2个 C.3个 D.4个-23B3.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2 C.1 D.- 1
4.若点A(1-a,5),B(3 ,b)关于y轴对称,求(2a,-b)的坐标,指出它在第几象限?B(8,-5)第四象限 5.已知点P (2a+b,-3a)与点 P′ (8,b+2).
若点p与点p′关于x轴对称,求a、 b的值.
若点p与点p′关于y轴对称,求a、 b的值.本节课你学到了什么?感悟与反思祝同学们学习进步!再见!
点的坐标变化与图形变化之间的关系.3.教学难点
点坐标变化与图形变化之间的变化规律.在如图所示的平面直
角坐标系中,第一、
二象限内各有一面小
旗.
(1)两面小旗之间有
怎样的位置关系?对
应点A与A1的坐标又
有什么特点?其它对
应的点也有这个特点
吗?归纳 概括1.关于x轴对称的两点,它们的横坐标 ,
纵坐标 ;
2.关于y轴对称的两点,它们的横坐标 ,
纵坐标 .相同互为相反数相同互为相反数在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案. yx将所得图案的各个顶点的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案又有着怎样的位置关系呢? yx12345-1-2-30–1–2–3–4–51234-4-55yx两个图形关于y轴对称顶点坐标变化:
纵坐标保持不变,
横坐标都乘以-1
(为原横坐标的相
反数).归纳:纵坐标相同,
横坐标互为相反数
的两点关于y轴对称. 将各坐标的纵
坐标都乘以
-1,横坐标保
持不变,则图形
怎么变化?yx与原图形关于x轴对称 将各坐标的纵
坐标都乘以-1,
横坐标保持不
变,则图形怎么
变化?yx与原图形关于x轴对称归纳:横坐标相同,
纵坐标互为相反
数的两点关于x
轴对称.–5 将各坐标的纵坐标与横坐标都乘以-1,图形会变成什么样?yx与原图形关于原点中心对称归纳:
横,纵坐标都互
为相反数的两
点关于原点对称.例 已知△ABC 的三个顶点的坐标分别为A(-3,5),B(- 4,1),C (-1,3),作出△ABC 关于y 轴和x 轴对称的图形.····AB ′A ′C ′1.将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形( )
A. 关于X轴对称. B. 关于Y轴对称
C. 关于原点对称 D. 无法确定
2.点A(-3,2)与点B(-3,-2)的关系是( )
A.关于X轴对称 B.关于Y轴对称
C.关于原点对称 D.以上各项都不对
3.已知点M(3,-2),点N(a,b)是M点关于Y轴的对称点,则 a= , b= .
4.已知点P(a-1,5)和点Q(2,b-1)关于X轴对称,则
a= ,b= .A-3-23-4跟踪练习AA`(-4,-1) 如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于x轴和y 轴对称的图形.···C`(-3,-2)B`(-1,1)拔尖自助餐xy课堂检测1.已知点P(2a-3,4),点A(-1,2b+2),
(1)如果点P与点A关于x轴对称,那么a+b=___
(2)如果点P与点A关于y轴对称,那么a+b=___
2.已知A、B两点的坐标分别是(-2,3)和(2,3), 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( ) A.1个 B.2个 C.3个 D.4个-23B3.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2 C.1 D.- 1
4.若点A(1-a,5),B(3 ,b)关于y轴对称,求(2a,-b)的坐标,指出它在第几象限?B(8,-5)第四象限 5.已知点P (2a+b,-3a)与点 P′ (8,b+2).
若点p与点p′关于x轴对称,求a、 b的值.
若点p与点p′关于y轴对称,求a、 b的值.本节课你学到了什么?感悟与反思祝同学们学习进步!再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
