北师大版八年级上册课件5.4 应用二元一次方程组——增收节支
文档属性
| 名称 | 北师大版八年级上册课件5.4 应用二元一次方程组——增收节支 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-13 21:46:04 | ||
图片预览







文档简介
课件21张PPT。4 应用二元一次方程组—增收节支有养鱼专业户甲,用某精饲料养鱼(精饲料的优点:鱼生长快,产量高),投入成本1万元,到年底出售鲜鱼总收入2.6万元,他满意的说:我既获得了利润又对社会作出了贡献!
有养鱼专业户乙,用某粗饲料养鱼(粗饲料的优点:鱼生长慢,产量低),投入成本1万元,到年底出售鲜鱼总收入1.8万元,他高兴的说:1.知识目标
(1)应用列方程组解决“增收节支”型实际问题 .
(2)会借助列表法来分析题目的数量间关系,从而找出等量关系式.2.教学重点?
(1)初步体会列方程组解决实际问题的步骤.
(2)学会用图表分析较复杂的数量关系问题.
3.教学难点
将实际问题转化成二元一次方程组的数学模型;
会用图表分析数量关系. 某人去年每个月的工资是6000元,今年比去年增长了10%,则今年的工资为 元.如果要扣除5%的税,则还剩 元.660062701.增长率公式原来的量× =后来的量(1+增长率)2.银行利率问题中的公式(利息、本金、利率)利息=本金×利率×期数(几年期)本息和=本金+利息 某人按定期一年存入银行10000元,若年利率为2.25%,则一年后可得利息_______元;本息和为_________元
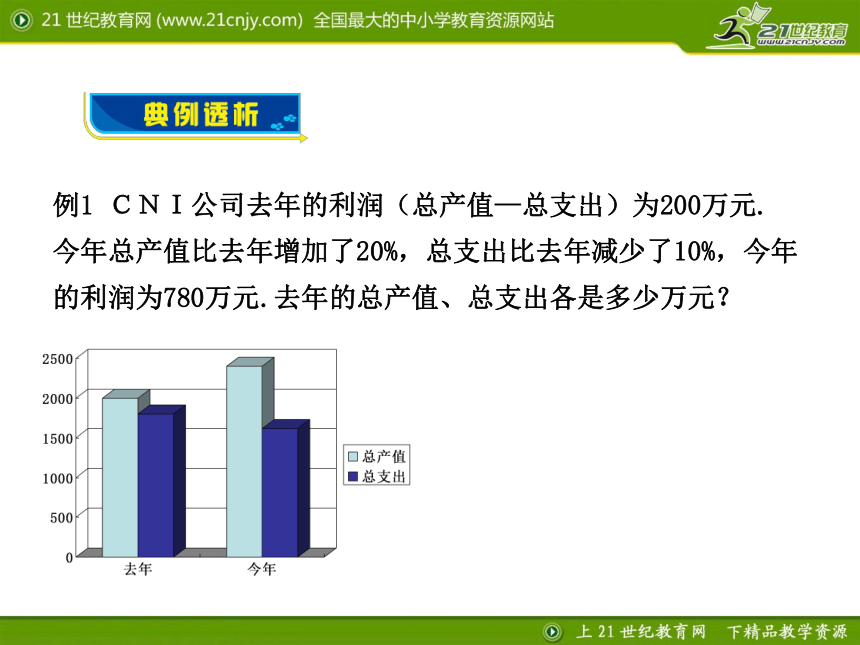
(不考虑利息税).22510225 某商品进价为2000元,卖出后可获利50%,则利润为 元,该商品的售价为 元.100030003.利润、利润率公式进价× =利润利润率售价— =利润进价例1 CNI公司去年的利润(总产值—总支出)为200万元.
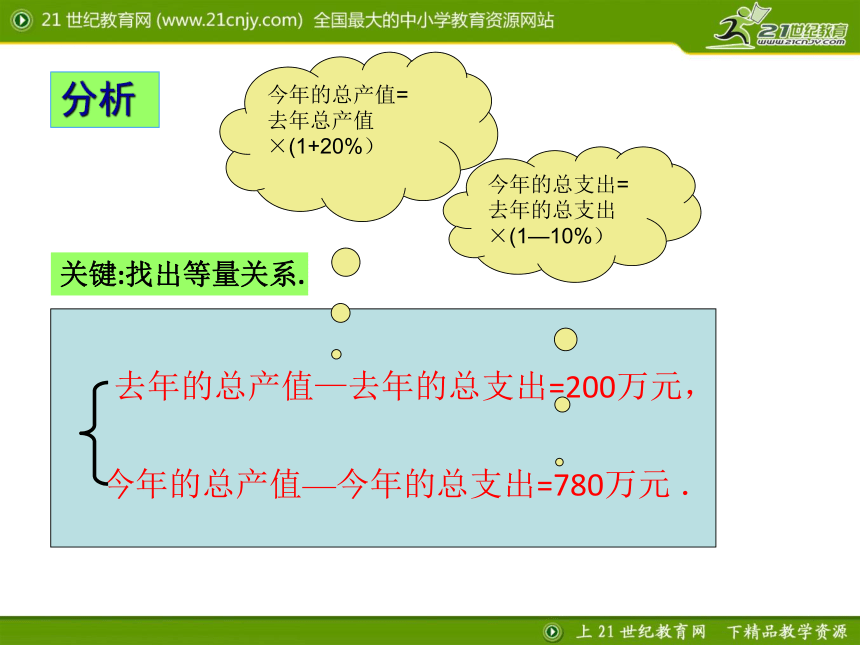
今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元? 去年的总产值—去年的总支出=200万元, 今年的总产值—今年的总支出=780万元 .分析关键:找出等量关系.今年的总支出=去年的总支出×(1—10%)今年的总产值=
去年总产值×(1+20%) 解:设去年的总产值为x万元,总支出为y万元,则
今年的总产值=(1+20%)x万元,
今年的总支出=(1—10%)y万元.
由题意得:解得答:去年的总收入为2000万元,总支出为1800万元. 议一议:还可以设间接未知数吗?①② 例2 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙原料各多少克恰好满足病人的需要?解:设每餐甲、乙原料各x,y克. 则有下表:0.5xx0.7y0.4y3540解:设每餐甲、乙原料各x克,y克. 根据题意得:5x+7y=350, ①5x+2y=200. ②0.5x+0.7y=35,x+0.4y=40.化简,得①- ②,得 5y=150,y=30.把y=30代入①,得x=28.答:每餐需甲原料28克、乙原料30克.跟踪检测 1.一、二班共有100名学生,他们的体育达标率(达到标准的百分率)为81﹪,如果一班学生的体育达标率为87.5﹪,二班学生的体育达标率为75﹪,那么一、二班的学生数各是多少?设一、二班的学生分别为x名,y名.填写下表并求出x,y的值.xy10087. 5﹪x75﹪y81﹪×100 2. 甲、乙两人从相距36千米的两地相向而行,如甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每时各走多少千米? 设甲、乙两人每小时分别行走x千米,y千米.填写下表并求出x,y的值.(2+2.5)x2.5y36363x(2+3)y解得x=6,y=3.6.(2+2.5)x+2.5y=36,3x+(2+3)y=36. 3.某人以两种形式存8000元,一种储蓄的年利率为10%,
另一种储蓄的年利率为11%.一年到期后,他共得利息855元(没有利息税),问两种储蓄他各存了多少钱?设年利率为11%的存x元,年利率10%存 y元.则x + y=8000,11%x+10%y=855.x =5500, y=2500.小明想开一家时尚G点专卖店,开店前他到其他专卖店调查价格.他看中了一套新款春装,成本共500元,专卖店店员告诉他在上市时通常将上衣按50﹪的利润定价,裤子按40﹪的利润定价.在实际出售时,为吸引顾客,两件服装均按9折出售,这样专卖店共获利157元,你知道上衣和裤子的成本各是多少元吗?xy解:设上衣的成本价为x元,裤子的成本价为y元:拔尖自助餐当堂检测
1.有甲乙两种溶液,甲种溶液由酒精1升,水3升配制而成;乙种溶液由酒精3升,水2升配制而成.现要配制浓度为50%的酒精溶液7升,甲乙两种溶液应各取几升?解:设甲种溶液需x升,乙种溶液需y升,
则有x + y=7,25%x + 60%y=50%×7.解得:y =5.x=2,2. 某公司用30000元购进甲乙两种货物.货物卖出后,甲种
货物获利10%,乙种货物获利11%,共得利润3150元,问两种
货物各进多少钱的货?设甲种货物进x元的货,乙种货物进 y元的货.x +y=30000,10%x + 11%y=3150.x=15000,y=15000.3. 用含糖分别为35%和40%的两种糖水混合,配制成含糖36%的糖水50千克,每种糖水应各取多少千克?设应取35%的糖水x千克,40%的糖水y千克.则: x+ y=50,35% x + 40%y=50×36%.x =40,y=10.本节课你学到了什么?感悟与反思 1、借助列表法分析具体问题中蕴含的数量关系,列出方程组,然后解出二元一次方程组从而解决实际问题.
2、在“增收节支”型问题中,要理解关键词“增加 、减少 、增长率、降低率”等 .祝同学们学习进步!再见!
有养鱼专业户乙,用某粗饲料养鱼(粗饲料的优点:鱼生长慢,产量低),投入成本1万元,到年底出售鲜鱼总收入1.8万元,他高兴的说:1.知识目标
(1)应用列方程组解决“增收节支”型实际问题 .
(2)会借助列表法来分析题目的数量间关系,从而找出等量关系式.2.教学重点?
(1)初步体会列方程组解决实际问题的步骤.
(2)学会用图表分析较复杂的数量关系问题.
3.教学难点
将实际问题转化成二元一次方程组的数学模型;
会用图表分析数量关系. 某人去年每个月的工资是6000元,今年比去年增长了10%,则今年的工资为 元.如果要扣除5%的税,则还剩 元.660062701.增长率公式原来的量× =后来的量(1+增长率)2.银行利率问题中的公式(利息、本金、利率)利息=本金×利率×期数(几年期)本息和=本金+利息 某人按定期一年存入银行10000元,若年利率为2.25%,则一年后可得利息_______元;本息和为_________元
(不考虑利息税).22510225 某商品进价为2000元,卖出后可获利50%,则利润为 元,该商品的售价为 元.100030003.利润、利润率公式进价× =利润利润率售价— =利润进价例1 CNI公司去年的利润(总产值—总支出)为200万元.
今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元? 去年的总产值—去年的总支出=200万元, 今年的总产值—今年的总支出=780万元 .分析关键:找出等量关系.今年的总支出=去年的总支出×(1—10%)今年的总产值=
去年总产值×(1+20%) 解:设去年的总产值为x万元,总支出为y万元,则
今年的总产值=(1+20%)x万元,
今年的总支出=(1—10%)y万元.
由题意得:解得答:去年的总收入为2000万元,总支出为1800万元. 议一议:还可以设间接未知数吗?①② 例2 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙原料各多少克恰好满足病人的需要?解:设每餐甲、乙原料各x,y克. 则有下表:0.5xx0.7y0.4y3540解:设每餐甲、乙原料各x克,y克. 根据题意得:5x+7y=350, ①5x+2y=200. ②0.5x+0.7y=35,x+0.4y=40.化简,得①- ②,得 5y=150,y=30.把y=30代入①,得x=28.答:每餐需甲原料28克、乙原料30克.跟踪检测 1.一、二班共有100名学生,他们的体育达标率(达到标准的百分率)为81﹪,如果一班学生的体育达标率为87.5﹪,二班学生的体育达标率为75﹪,那么一、二班的学生数各是多少?设一、二班的学生分别为x名,y名.填写下表并求出x,y的值.xy10087. 5﹪x75﹪y81﹪×100 2. 甲、乙两人从相距36千米的两地相向而行,如甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每时各走多少千米? 设甲、乙两人每小时分别行走x千米,y千米.填写下表并求出x,y的值.(2+2.5)x2.5y36363x(2+3)y解得x=6,y=3.6.(2+2.5)x+2.5y=36,3x+(2+3)y=36. 3.某人以两种形式存8000元,一种储蓄的年利率为10%,
另一种储蓄的年利率为11%.一年到期后,他共得利息855元(没有利息税),问两种储蓄他各存了多少钱?设年利率为11%的存x元,年利率10%存 y元.则x + y=8000,11%x+10%y=855.x =5500, y=2500.小明想开一家时尚G点专卖店,开店前他到其他专卖店调查价格.他看中了一套新款春装,成本共500元,专卖店店员告诉他在上市时通常将上衣按50﹪的利润定价,裤子按40﹪的利润定价.在实际出售时,为吸引顾客,两件服装均按9折出售,这样专卖店共获利157元,你知道上衣和裤子的成本各是多少元吗?xy解:设上衣的成本价为x元,裤子的成本价为y元:拔尖自助餐当堂检测
1.有甲乙两种溶液,甲种溶液由酒精1升,水3升配制而成;乙种溶液由酒精3升,水2升配制而成.现要配制浓度为50%的酒精溶液7升,甲乙两种溶液应各取几升?解:设甲种溶液需x升,乙种溶液需y升,
则有x + y=7,25%x + 60%y=50%×7.解得:y =5.x=2,2. 某公司用30000元购进甲乙两种货物.货物卖出后,甲种
货物获利10%,乙种货物获利11%,共得利润3150元,问两种
货物各进多少钱的货?设甲种货物进x元的货,乙种货物进 y元的货.x +y=30000,10%x + 11%y=3150.x=15000,y=15000.3. 用含糖分别为35%和40%的两种糖水混合,配制成含糖36%的糖水50千克,每种糖水应各取多少千克?设应取35%的糖水x千克,40%的糖水y千克.则: x+ y=50,35% x + 40%y=50×36%.x =40,y=10.本节课你学到了什么?感悟与反思 1、借助列表法分析具体问题中蕴含的数量关系,列出方程组,然后解出二元一次方程组从而解决实际问题.
2、在“增收节支”型问题中,要理解关键词“增加 、减少 、增长率、降低率”等 .祝同学们学习进步!再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
