六年级下册数学苏教版选择策略解决问题课件(共20张PPT)
文档属性
| 名称 | 六年级下册数学苏教版选择策略解决问题课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 22:07:21 | ||
图片预览









文档简介
(共20张PPT)
三年级上册
三年级下册
四年级上册
四年级下册
五年级下册
五年级上册
六年级上册
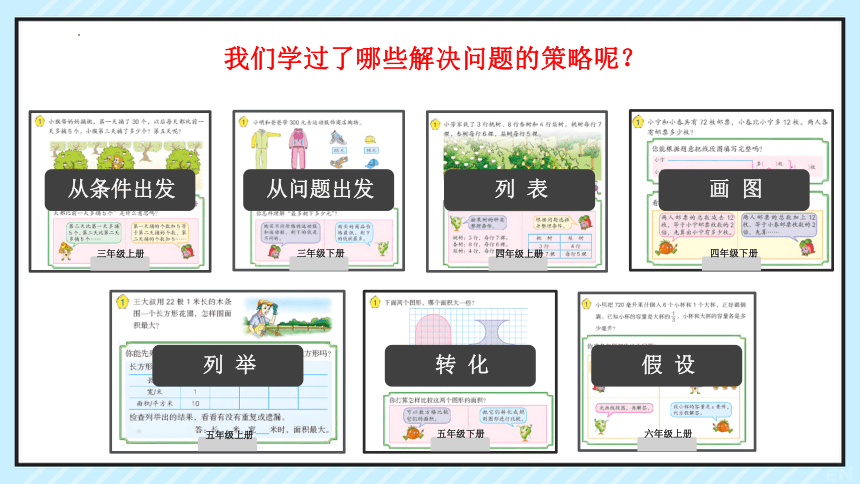
从条件出发
从问题出发
列 表
画 图
列 举
转 化
假 设
我们学过了哪些解决问题的策略呢?
选择策略
解决实际问题
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
信息整理
全班
42人
大船
5人/只
小船
3人/只
10只
可坐
人数
只
只
猜一猜大船和小船可能各有多少只?
确定好策略后,再小组讨论交流右侧问题。
1.怎样想到先画10只大船的?
5.是按什么样的顺序进行列举的?为什么?
6.每次将大船只数减少1只,小船只数增加1只
后,坐的总人数发生了什么样的变化?
7.根据表中第一栏的数据可以知道什么?
8.你是怎样进行调整的?
2.在船上划去2人表示什么?
3.为什么把4只大船换成小船?
4.先画10只小船也可以得到答案吗?试一试。
假 设
列 举
画 图
9.假设大船有x只,你能列方程解答吗?试一试?
你准备用什么策略解决这个问题呢?
(课本第28页呈现了3种解题思路)
先画10只大船坐50人
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图
想:
去掉多余8人
大船改小船,每只船去掉2人
8÷2=4,要改 大船为小船
( 5-3=2 )
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图
先画10只小船坐30人
想:
增加12人
小船改大船,每只船增加2人
12÷2=6,要改6只大船为小船
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列举
从大船有9只,小船有1只开始列举。
有序列举。
8
2
8×5+2×3=46
多了4人
7
3
7×5+3×3=44
多了2人
6
4
6×5+4×3=42
刚好
5
5
5×5+5×3=40
少了2人
还要往下列举吗?
答:租大船6只,小船4只。
+1
+1
+1
+1
-2
-2
-2
-2
假设-调整
假设大船和小船同样多
想:
6
4
6×5+4×3=42
刚好
少了2人
对比总人数,进行调整
(船的座位数少,增加大船只数)
答:租大船6只,小船4只。
1.假设前适当分析,从接近实际
结果的数据开始假设;
为什么从5只大船和5只小船开始假设?
2.数感。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列式计算
你会怎样解答呢
按画图的思路来解答:
5×10=50(人)
50-42=8(人)
5-3=2(人)
8÷2=4(只)
10-4=6(只)
假设有10只大船
比实际总人数多了8人
大船与小船相差的人数
小船:
大船:
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列式计算
3×10=30(人)
42-30=12(人)
5-3=2(人)
12÷2=6(只)
10-6=4(只)
假设有10只小船
比实际总人数相差的人数
大船与小船相差的人数
大船:
小船:
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
假设
解:设大船有x只;
则:小船有(10-x)只。
5x+3×(10-x)=42
5x+30-3x=42
2x=12
x=6
10-x=10-6=4
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
检验:
6+4=10(只)
5×6+3×4=42(人)
画图
列举
假设-调整
比较这几种思路,它们有什么联系和区别?
联系:无论是画图还是列举,都是
先假设,再对数据进行调整。
区别:画图策略更直观清楚。
列举策略能有条理的一一列举;
假设策略更快捷。
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(根据下面的提示,选择一种方法找出答案。)
①画8个圆,表示一共有8只动物。
②假设8只都是鸡,给每只动物画2条腿。
算一算画出的腿比22条少多少条。
③一只兔比一只鸡多2条腿,给其中的几只
动物添上2条腿,使画出的腿正好是22条。
④鸡有( )只,兔有( )只。
(1)按照下面的步骤画图。
(2)先假设鸡和兔同样多,
再调整。
都是先假设,再对数据进行调整。
回顾(1)和(2)的方法,它们有什么相同之处?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(你会列算式解答吗?)
答:鸡有5只,兔有3只。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(3)
8×4=32(条)
一般选择假设成都是腿比较多的兔子,计算比较简单。
32-22=10(条)
4-2=2(条)
鸡:10÷2=5(只)
兔:8-5=3(只)
(3)设兔有x只,则鸡有(8-x)只。
(根据下面的提示,列方程解答。)
4x+2×(8-x)=22
4x+16-2x=22
2x=6
x=3
8-x=8-3=5
答:鸡有5只,兔有3只。
一般选择腿多的动物设为x,解方程简单。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
“
”
鸡兔同笼
画图、列举、假设的策略都可以解决 “鸡兔同笼”类问题。
相当于
六年级同学制作了78件蝴蝶标本,贴在9块展板上展出。每块小展板贴6件,每块大展板贴10件。两种展板各有多少块
用画图或列举的策略方便吗?若是100件、200件呢?
回顾解决问题的过程,你有哪些体会?
画图、列举、先假设再调整的策略都可以解决 “鸡兔同笼”类问题。
1
分析和解决同一个问题,可以用不同的策略。
2
要学会根据具体的问题灵活选择策略。
3
三年级上册
三年级下册
四年级上册
四年级下册
五年级下册
五年级上册
六年级上册
从条件出发
从问题出发
列 表
画 图
列 举
转 化
假 设
我们学过了哪些解决问题的策略呢?
选择策略
解决实际问题
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
信息整理
全班
42人
大船
5人/只
小船
3人/只
10只
可坐
人数
只
只
猜一猜大船和小船可能各有多少只?
确定好策略后,再小组讨论交流右侧问题。
1.怎样想到先画10只大船的?
5.是按什么样的顺序进行列举的?为什么?
6.每次将大船只数减少1只,小船只数增加1只
后,坐的总人数发生了什么样的变化?
7.根据表中第一栏的数据可以知道什么?
8.你是怎样进行调整的?
2.在船上划去2人表示什么?
3.为什么把4只大船换成小船?
4.先画10只小船也可以得到答案吗?试一试。
假 设
列 举
画 图
9.假设大船有x只,你能列方程解答吗?试一试?
你准备用什么策略解决这个问题呢?
(课本第28页呈现了3种解题思路)
先画10只大船坐50人
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图
想:
去掉多余8人
大船改小船,每只船去掉2人
8÷2=4,要改 大船为小船
( 5-3=2 )
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图
先画10只小船坐30人
想:
增加12人
小船改大船,每只船增加2人
12÷2=6,要改6只大船为小船
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列举
从大船有9只,小船有1只开始列举。
有序列举。
8
2
8×5+2×3=46
多了4人
7
3
7×5+3×3=44
多了2人
6
4
6×5+4×3=42
刚好
5
5
5×5+5×3=40
少了2人
还要往下列举吗?
答:租大船6只,小船4只。
+1
+1
+1
+1
-2
-2
-2
-2
假设-调整
假设大船和小船同样多
想:
6
4
6×5+4×3=42
刚好
少了2人
对比总人数,进行调整
(船的座位数少,增加大船只数)
答:租大船6只,小船4只。
1.假设前适当分析,从接近实际
结果的数据开始假设;
为什么从5只大船和5只小船开始假设?
2.数感。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列式计算
你会怎样解答呢
按画图的思路来解答:
5×10=50(人)
50-42=8(人)
5-3=2(人)
8÷2=4(只)
10-4=6(只)
假设有10只大船
比实际总人数多了8人
大船与小船相差的人数
小船:
大船:
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
列式计算
3×10=30(人)
42-30=12(人)
5-3=2(人)
12÷2=6(只)
10-6=4(只)
假设有10只小船
比实际总人数相差的人数
大船与小船相差的人数
大船:
小船:
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
假设
解:设大船有x只;
则:小船有(10-x)只。
5x+3×(10-x)=42
5x+30-3x=42
2x=12
x=6
10-x=10-6=4
答:租大船6只,小船4只。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
检验:
6+4=10(只)
5×6+3×4=42(人)
画图
列举
假设-调整
比较这几种思路,它们有什么联系和区别?
联系:无论是画图还是列举,都是
先假设,再对数据进行调整。
区别:画图策略更直观清楚。
列举策略能有条理的一一列举;
假设策略更快捷。
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(根据下面的提示,选择一种方法找出答案。)
①画8个圆,表示一共有8只动物。
②假设8只都是鸡,给每只动物画2条腿。
算一算画出的腿比22条少多少条。
③一只兔比一只鸡多2条腿,给其中的几只
动物添上2条腿,使画出的腿正好是22条。
④鸡有( )只,兔有( )只。
(1)按照下面的步骤画图。
(2)先假设鸡和兔同样多,
再调整。
都是先假设,再对数据进行调整。
回顾(1)和(2)的方法,它们有什么相同之处?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(你会列算式解答吗?)
答:鸡有5只,兔有3只。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
(3)
8×4=32(条)
一般选择假设成都是腿比较多的兔子,计算比较简单。
32-22=10(条)
4-2=2(条)
鸡:10÷2=5(只)
兔:8-5=3(只)
(3)设兔有x只,则鸡有(8-x)只。
(根据下面的提示,列方程解答。)
4x+2×(8-x)=22
4x+16-2x=22
2x=6
x=3
8-x=8-3=5
答:鸡有5只,兔有3只。
一般选择腿多的动物设为x,解方程简单。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
1.
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
“
”
鸡兔同笼
画图、列举、假设的策略都可以解决 “鸡兔同笼”类问题。
相当于
六年级同学制作了78件蝴蝶标本,贴在9块展板上展出。每块小展板贴6件,每块大展板贴10件。两种展板各有多少块
用画图或列举的策略方便吗?若是100件、200件呢?
回顾解决问题的过程,你有哪些体会?
画图、列举、先假设再调整的策略都可以解决 “鸡兔同笼”类问题。
1
分析和解决同一个问题,可以用不同的策略。
2
要学会根据具体的问题灵活选择策略。
3
