2023-2024学年华东师大版八年级数学下册第19章 矩形菱形与正方形 单元练习(无答案)
文档属性
| 名称 | 2023-2024学年华东师大版八年级数学下册第19章 矩形菱形与正方形 单元练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 629.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 11:47:59 | ||
图片预览

文档简介
八年级数学华师版
矩形、菱形与正方形单元练习
(满分 120分, 建议用时 100分钟)
学校 姓名 班级
一、选择题 (每小题3分,共30分)
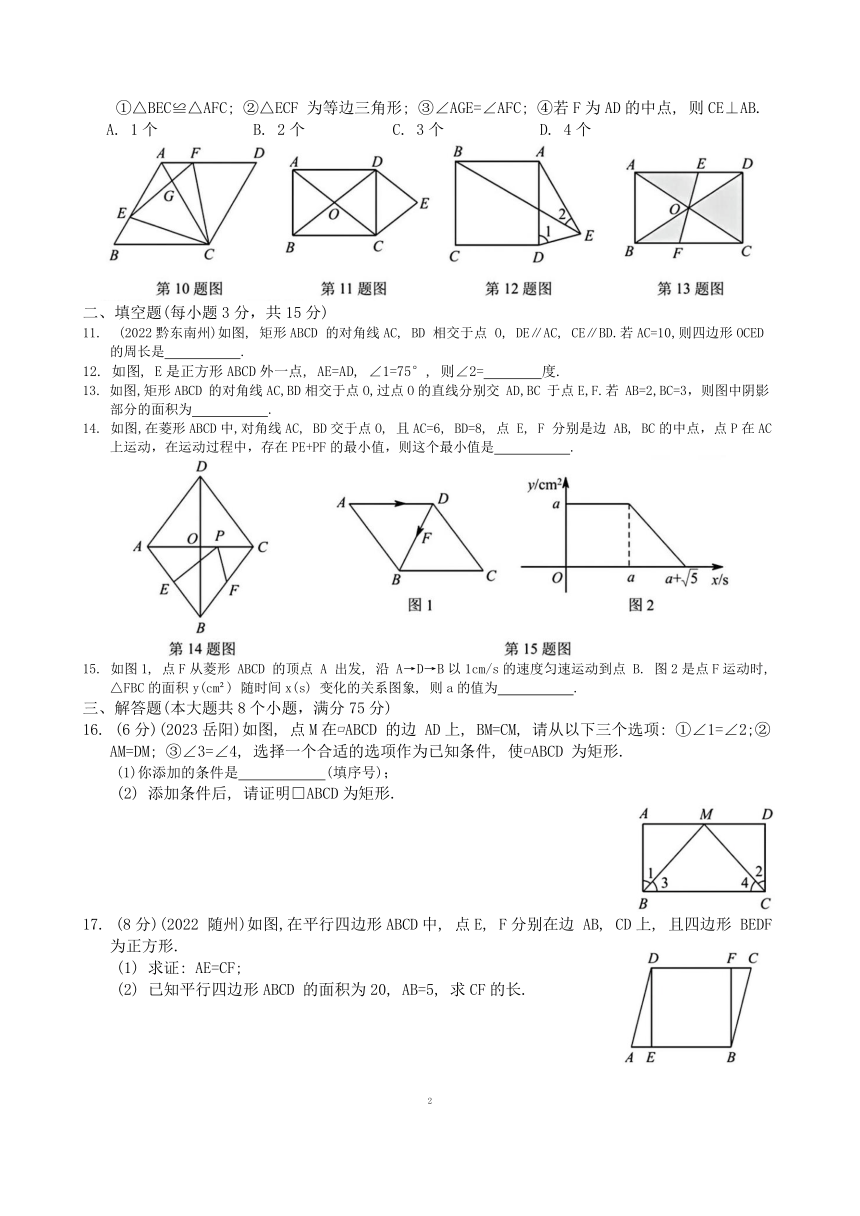
1. 菱形具有而平行四边形不一定具有的性质是( )
A.邻边相等 B.对边相等 C.对角相等 D.是中心对称图形
2. (2022 陕西) 在下列条件中, 能够判定□ABCD 为矩形的是 ( )
A. AB=AD B. AC⊥BD C. AB=AC D. AC=BD
3. (2023 深圳)如图,在平行四边形ABCD中, AB=4, BC=6, 将线段AB 水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为 ( )
A. 1 B. 2 C. 3 D. 4
4. 如图, 在矩形ABCD 中, DE平分∠ADC交BC于点E, 连接AE, 若CD=6, AE=10, 则AD的长为( )
A. 12 B. 14 C. 16 D. 20
5. (2021 玉林)一个四边形顺次添加下列条件中的三个便得到正方形:
a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件: ①a→c→d; ②b→d→c; ③a→b→c, 则正确的是 ( )
A. 仅① B. 仅③ C. ①② D. ②③
6. (2023 十堰)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是 ( )
A.四边形ABCD 由矩形变为平行四边形 B.对角线BD 的长度减小
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
7. 如图,在正方形ABCD 中, AC为对角线,点E 在AB 边上, EF⊥AC于点 F, 连接EC, AF=3,△EFC的周长为12, 则 EC的长为 ( )
A. 3 B. 4 C. 5 D. 10
8. 如图,在菱形ABCD中,∠BCD=110°, CD的垂直平分线交对角线AC于点 F, 垂足为点 E, 连接BF, 则∠ABF等于( )
A. 10° B. 15° C. 20° D. 25°
9. 如图, 矩形ABCD中,对角线AC与BD 交于点O, AB=3, BC=4, 点 P为边AD 上的动点, PE⊥AC于点 E, PF⊥BD于点F, 则PE+PF的值为 ( )
A. C. 5 D. 7
10. 如图,已知菱形ABCD, ∠BAD=120°, E, F分别是AB, AD边上的动点, 且BE=AF, 则下列结论正确的有 ( )
①△BEC≌△AFC; ②△ECF 为等边三角形; ③∠AGE=∠AFC; ④若F为AD的中点, 则CE⊥AB.
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每小题3分,共15分)
11. (2022黔东南州)如图, 矩形ABCD 的对角线AC, BD 相交于点 O, DE∥AC, CE∥BD.若AC=10,则四边形OCED 的周长是 .
12. 如图, E是正方形ABCD外一点, AE=AD, ∠1=75°, 则∠2= 度.
13. 如图,矩形ABCD 的对角线AC,BD相交于点O,过点O的直线分别交 AD,BC 于点E,F.若 AB=2,BC=3,则图中阴影部分的面积为 .
14. 如图,在菱形ABCD中,对角线AC, BD交于点O, 且AC=6, BD=8, 点 E, F 分别是边 AB, BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 .
15. 如图1, 点F从菱形 ABCD 的顶点 A 出发, 沿 A→D→B以1cm/s的速度匀速运动到点 B. 图2是点F运动时,△FBC的面积y(cm ) 随时间x(s) 变化的关系图象, 则a的值为 .
三、解答题(本大题共8个小题,满分75分)
16. (6分)(2023岳阳)如图, 点M在 ABCD 的边 AD上, BM=CM, 请从以下三个选项: ①∠1=∠2;②AM=DM; ③∠3=∠4, 选择一个合适的选项作为已知条件, 使 ABCD 为矩形.
(1)你添加的条件是 (填序号);
(2) 添加条件后, 请证明□ABCD为矩形.
17. (8分)(2022 随州)如图,在平行四边形ABCD中, 点E, F分别在边 AB, CD上, 且四边形 BEDF为正方形.
(1) 求证: AE=CF;
(2) 已知平行四边形ABCD 的面积为20, AB=5, 求CF的长.
2
18. (8分)(2023湘西州)如图, 四边形ABCD 是平行四边形, BM∥DN, 且分别交对角线AC于点M,N, 连接MD, BN.
(1) 求证: ∠DMN=∠BNM;
(2) 若∠BAC=∠DAC. 求证: 四边形BMDN是菱形.
19. (10分)(2022巴中)如图,□ABCD中,E为BC边的中点, 连接AE 并延长交 DC 的延长线于点 F,延长EC至点G, 使CG=CE, 连接DG, DE, FG.
(1) 求证: △ABE≌△FCE;
(2) 若AD=2AB, 求证: 四边形DEFG 是矩形.
20. (10分) 实践与探究
(1)操作一:如图1,已知正方形纸片 ABCD,将正方形纸片沿过点A的直线折叠,使点 B落在正方形 ABCD 的内部,点 B 的对应点为点 M,折痕为 AE,再将纸片沿过点 A 的直线折叠,使 AD 与AM 重合, 折痕为AF, 则 度.
(2)操作二:如图2,将正方形纸片沿EF继续折叠,点 C 的对应点为点 N,点 N 恰好落在折痕 AE上;
度;
②设AM与NF的交点为P. 求证:
3
21. (10分) 如图所示, AD∥BC, ∠BAD=90°, 以B为圆心, BC长为半径画弧,与射线AD 相交于点E, 连接BE, 过C 作 CF⊥BE 于点F.
(1)线段BF 与图中哪条线段相等 写出来并加以证明.
(2) 若 AB=12, BC=13, P 从 E沿ED 方向运动, Q从C出发向 B 运动,两点同时出发且速度均为每秒1 个单位长度.
①当t= 秒时, 四边形EPCQ 是矩形;
②当t= 秒时, 四边形 EPCQ 是菱形.
22. (11分) 阅读以下材料,并按要求完成相应的任务. 如图1,已知四边形 ABCD 的对角线AC,BD相交于点O, 点M是BC边的中点,过点M作ME∥AC交BD于点E, 作MF∥BD交AC于点F,我们称四边形OEMF为四边形ABCD的“伴随四边形”.
(1)若四边形ABCD 是菱形,则其“伴随四边形”是 ,若四边形 ABCD 是矩形,则其“伴随四边形”是 (在横线上填特殊平行四边形的名称);
(2)如图2,若四边形ABCD 是矩形,M是BC延长线上的一个动点,其他条件不变,点F落在AC的延长线上,请写出线段OB,ME,MF之间的数量关系,并说明理由.
23. (12分)如图1, 在正方形ABCD中,∠AEF=90°, 且EF交正方形外角的平分线CF于点F.
(1) 若点 E是BC边上的中点, 求证: AE=EF(提示: 取AB的中点H,连接EH).
(2)如图2,若点E是 BC的延长线上(除C点外)的任意一点,其他条件不变,那么结论 是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由.
(3)如图3,若点E是 BC边上的任意一点,在AB边上是否存在点M,使得四边形 DMEF 是平行四边形 若存在,请直接写出点M满足的条件;若不存在,请说明理由.
4
矩形、菱形与正方形单元练习
(满分 120分, 建议用时 100分钟)
学校 姓名 班级
一、选择题 (每小题3分,共30分)
1. 菱形具有而平行四边形不一定具有的性质是( )
A.邻边相等 B.对边相等 C.对角相等 D.是中心对称图形
2. (2022 陕西) 在下列条件中, 能够判定□ABCD 为矩形的是 ( )
A. AB=AD B. AC⊥BD C. AB=AC D. AC=BD
3. (2023 深圳)如图,在平行四边形ABCD中, AB=4, BC=6, 将线段AB 水平向右平移a个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为 ( )
A. 1 B. 2 C. 3 D. 4
4. 如图, 在矩形ABCD 中, DE平分∠ADC交BC于点E, 连接AE, 若CD=6, AE=10, 则AD的长为( )
A. 12 B. 14 C. 16 D. 20
5. (2021 玉林)一个四边形顺次添加下列条件中的三个便得到正方形:
a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件: ①a→c→d; ②b→d→c; ③a→b→c, 则正确的是 ( )
A. 仅① B. 仅③ C. ①② D. ②③
6. (2023 十堰)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是 ( )
A.四边形ABCD 由矩形变为平行四边形 B.对角线BD 的长度减小
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
7. 如图,在正方形ABCD 中, AC为对角线,点E 在AB 边上, EF⊥AC于点 F, 连接EC, AF=3,△EFC的周长为12, 则 EC的长为 ( )
A. 3 B. 4 C. 5 D. 10
8. 如图,在菱形ABCD中,∠BCD=110°, CD的垂直平分线交对角线AC于点 F, 垂足为点 E, 连接BF, 则∠ABF等于( )
A. 10° B. 15° C. 20° D. 25°
9. 如图, 矩形ABCD中,对角线AC与BD 交于点O, AB=3, BC=4, 点 P为边AD 上的动点, PE⊥AC于点 E, PF⊥BD于点F, 则PE+PF的值为 ( )
A. C. 5 D. 7
10. 如图,已知菱形ABCD, ∠BAD=120°, E, F分别是AB, AD边上的动点, 且BE=AF, 则下列结论正确的有 ( )
①△BEC≌△AFC; ②△ECF 为等边三角形; ③∠AGE=∠AFC; ④若F为AD的中点, 则CE⊥AB.
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每小题3分,共15分)
11. (2022黔东南州)如图, 矩形ABCD 的对角线AC, BD 相交于点 O, DE∥AC, CE∥BD.若AC=10,则四边形OCED 的周长是 .
12. 如图, E是正方形ABCD外一点, AE=AD, ∠1=75°, 则∠2= 度.
13. 如图,矩形ABCD 的对角线AC,BD相交于点O,过点O的直线分别交 AD,BC 于点E,F.若 AB=2,BC=3,则图中阴影部分的面积为 .
14. 如图,在菱形ABCD中,对角线AC, BD交于点O, 且AC=6, BD=8, 点 E, F 分别是边 AB, BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 .
15. 如图1, 点F从菱形 ABCD 的顶点 A 出发, 沿 A→D→B以1cm/s的速度匀速运动到点 B. 图2是点F运动时,△FBC的面积y(cm ) 随时间x(s) 变化的关系图象, 则a的值为 .
三、解答题(本大题共8个小题,满分75分)
16. (6分)(2023岳阳)如图, 点M在 ABCD 的边 AD上, BM=CM, 请从以下三个选项: ①∠1=∠2;②AM=DM; ③∠3=∠4, 选择一个合适的选项作为已知条件, 使 ABCD 为矩形.
(1)你添加的条件是 (填序号);
(2) 添加条件后, 请证明□ABCD为矩形.
17. (8分)(2022 随州)如图,在平行四边形ABCD中, 点E, F分别在边 AB, CD上, 且四边形 BEDF为正方形.
(1) 求证: AE=CF;
(2) 已知平行四边形ABCD 的面积为20, AB=5, 求CF的长.
2
18. (8分)(2023湘西州)如图, 四边形ABCD 是平行四边形, BM∥DN, 且分别交对角线AC于点M,N, 连接MD, BN.
(1) 求证: ∠DMN=∠BNM;
(2) 若∠BAC=∠DAC. 求证: 四边形BMDN是菱形.
19. (10分)(2022巴中)如图,□ABCD中,E为BC边的中点, 连接AE 并延长交 DC 的延长线于点 F,延长EC至点G, 使CG=CE, 连接DG, DE, FG.
(1) 求证: △ABE≌△FCE;
(2) 若AD=2AB, 求证: 四边形DEFG 是矩形.
20. (10分) 实践与探究
(1)操作一:如图1,已知正方形纸片 ABCD,将正方形纸片沿过点A的直线折叠,使点 B落在正方形 ABCD 的内部,点 B 的对应点为点 M,折痕为 AE,再将纸片沿过点 A 的直线折叠,使 AD 与AM 重合, 折痕为AF, 则 度.
(2)操作二:如图2,将正方形纸片沿EF继续折叠,点 C 的对应点为点 N,点 N 恰好落在折痕 AE上;
度;
②设AM与NF的交点为P. 求证:
3
21. (10分) 如图所示, AD∥BC, ∠BAD=90°, 以B为圆心, BC长为半径画弧,与射线AD 相交于点E, 连接BE, 过C 作 CF⊥BE 于点F.
(1)线段BF 与图中哪条线段相等 写出来并加以证明.
(2) 若 AB=12, BC=13, P 从 E沿ED 方向运动, Q从C出发向 B 运动,两点同时出发且速度均为每秒1 个单位长度.
①当t= 秒时, 四边形EPCQ 是矩形;
②当t= 秒时, 四边形 EPCQ 是菱形.
22. (11分) 阅读以下材料,并按要求完成相应的任务. 如图1,已知四边形 ABCD 的对角线AC,BD相交于点O, 点M是BC边的中点,过点M作ME∥AC交BD于点E, 作MF∥BD交AC于点F,我们称四边形OEMF为四边形ABCD的“伴随四边形”.
(1)若四边形ABCD 是菱形,则其“伴随四边形”是 ,若四边形 ABCD 是矩形,则其“伴随四边形”是 (在横线上填特殊平行四边形的名称);
(2)如图2,若四边形ABCD 是矩形,M是BC延长线上的一个动点,其他条件不变,点F落在AC的延长线上,请写出线段OB,ME,MF之间的数量关系,并说明理由.
23. (12分)如图1, 在正方形ABCD中,∠AEF=90°, 且EF交正方形外角的平分线CF于点F.
(1) 若点 E是BC边上的中点, 求证: AE=EF(提示: 取AB的中点H,连接EH).
(2)如图2,若点E是 BC的延长线上(除C点外)的任意一点,其他条件不变,那么结论 是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由.
(3)如图3,若点E是 BC边上的任意一点,在AB边上是否存在点M,使得四边形 DMEF 是平行四边形 若存在,请直接写出点M满足的条件;若不存在,请说明理由.
4
