人教版九年级下册第二十七章《 27.1 图形的相似》ppt课件(40张)
文档属性
| 名称 | 人教版九年级下册第二十七章《 27.1 图形的相似》ppt课件(40张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-13 00:00:00 | ||
图片预览










文档简介
课件40张PPT。新课引入研读课文 展示目标 归纳小结 强化训练 第二十七章 相似第二十七章 相似
第一课时 27.1 图形的相似(1)一、新课引入 1、让同学们观察国徽上的五角星及教师准备
好的同底版不同尺寸的相片等等.
2、这些形状相同的图形之间,在数量关系和
位置关系上有什么规律吗?怎样才能按要求
放大和缩小一张美丽的相片?进入这一章学习吧,在实验,探究和论证之后,你会得出答案的。二、学习目标 从生活中形状相同的图形的实例
中认识图形的相似,理解相似图形
的概念.三、研读课文 认真阅读课本本章的内容,
完成下面练习并体验知识点的形
成过程.三、研读课文 知识点一:
相似图形的定义下图中,有用同一张底片洗出的不同
尺寸的照片,也有大小不同的足球,
还有一辆汽车和的模型.所有这些都给
我们一形状相同的形象,我们把这种
____________的图形叫做相似图形.形状相同三、研读课文 知识点一:
相似图形的定义
你能再举出相似图形的例子吗?三、研读课文 知识点一:
相似图形的定义
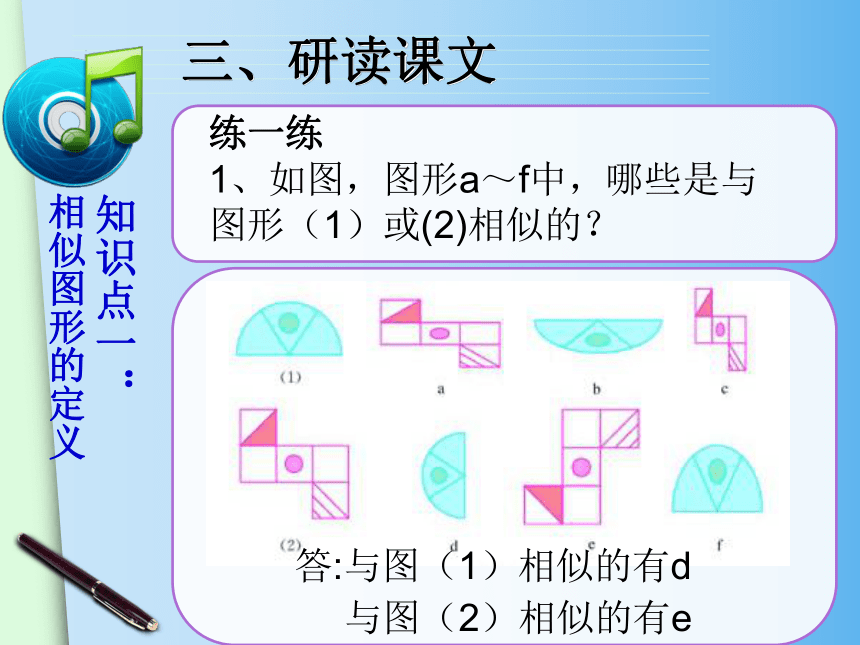
练一练
1、如图,图形a~f中,哪些是与
图形(1)或(2)相似的?答:与图(1)相似的有d与图(2)相似的有e三、研读课文 2、观察下列图形,指出哪些
是相似图形:答:是相似图形的有(1)与(8),
(2)与(6)知识点一:
相似图形的定义
三、研读课文 知识点二:相似图形
的来源两个图形相似,其中一个图形可以
看做是由另一个图形_________或
_________得到的,实际的建筑物
和它的模型是___________的,用
复印机把一个图形放大或缩小后所
得的图形,也是与原来的图
_________的.相似相似放大缩小三、研读课文 知识点二:相似图形
的来源
练一练1、如图,从放大镜里看到的三角尺
和原来的三角尺相似吗? 答:相似三、研读课文 知识点二:相似图形
的来源
2、如图,下面右边的四个图形中,
与左边的图形相似的是( )A三、研读课文 知识点二:相似图形
的来源
观察
下图是人们从平面镜及哈哈镜里
看懂的不同镜像,它们相似吗?总结:第一个图的两个图形______,
第二个图与第三个图的镜子中的
图像已变形,所以_________.相似不相似四、归纳小结 1、形状 的图形叫相似形.
2、两个图形相似,其中一个图形可以
看作由另一个图形的 或
而得到的.
3、学习反思:________________
_________________
______________________.相同放大缩小五、强化训练 1、下列说法正确的是( )
A.小明上幼儿园时的照片和初中毕业
时的照片相似.
B.商店新买来的一副三角板是相似的.
C.所有的课本都是相似的.
D.国旗的五角星都是相似的.D五、强化训练 2、下列说法中,错误的是( )
(A)两个全等三角形一定是相似形
(B)两个等腰三角形一定相似
(C)两个等边三角形一定相似
(D)两个等腰直角三角形一定相似B五、强化训练 3、在下列各组图形:
①两个平行四边形;②两个圆;
③两个矩形;④均有一个内角是80°的两个等腰三角形;
⑤两个正五边形;
⑥均有一个内角是100°的两个
等腰三角形.
其中一定是相似图形的是
.(填序号)②, ⑤, ⑥五、强化训练 4、在比例尺是1:8000000的“中国政区”
地图上,量得福州与上海之间的距离
是7.5cm,那么福州与上海之间的实
际距离是多少?解:设福州与上海之间的的实际距离是Xcm,
依题意得:答:福州与上海之间的的实际距离
是60千米五、强化训练 5、AB两地的实际距离为2500m,
在一张平面图上的距离是5cm,
那么这张平面地图的比例尺是多少?解:依题意可知,2500m=250000cm
故这张平面地图的比例尺是
答:这张平面地图的比例尺是 .
第二课时
27.1 图形的相似(2)名人名言:决心就是力量,
信心就是成功。---列夫.托尔斯泰一、新课引入 上节课我们介绍了什么样的图形是相似图形?
这节课我们将介绍两个相似图形都有哪些主要特征.
会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进行有关的计算. 二、学习目标 三、研读课文 知识点一 认真阅读课本第36至38页的内容,完成下面练习并体验知识点的形成过程. 相似多边形的性质观察(1)图27.1-4(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?三、研读课文 知识点一 相似多边形的性质解:△A1B1C1和△ABC相似
=====思考?(2)对于图27.1-4(2)中两个相似的正
六边形,是否也能得到类似的结论?是的三、研读课文
探究知识点一 相似多边形的性质如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形. 对于图中两个相似的四边形,它们
的对应角,对应边的比是否相等? (相等)问题三、研读课文 知识点一 相似多边形的性质结论: (1)相似多边形的特征:相似多边形的对应角______,对应边的比_______.
反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
相等相等相等相等相似 在⊿ABC和⊿A1B1C1中,
若 ,
则⊿ABC和⊿A1B1C1相似.
几何语言三、研读课文 知识点一 相似多边形的性质结论: (2)相似比:相似多边形________的比
称为相似比.
相似比为1时,相似的两个图形
______,
因此________形是一种特殊的相似形.
对应边全等全等三、研读课文 知识点一 相似多边形的性质(3)比例线段:对于四条线段 如果
与 相等
(如 ),(即___________)
我们就说这四条线段是成比例线段,简称
__________其中两条线段的比(即它们长度的比)另两条线段的比比例线段结论:三、研读课文 知识点一 相似多边形的性质 解:如图所示的两个直角三角形相似。
因为从图形标出的数据可看出这两个三角形
是等腰直角三角形,所以它们的对应角相等,对应边的比也相等,都等于1:2。 练一练:1、如图所示的两个直角
三角形相似吗?为什么?2、已知a、b、c、d是成比例线段,其中
a=2,b=5,c=3,则d=_____.7.5三、研读课文
知识点二 相似多边形性质的应用例 如图,四边形ABCD和EFGH相似,
求角 , 的大小和EH的长度 .三、研读课文
知识点二 相似多边形性质的应用三、研读课文
知识点二 相似多边形性质的应用练一练:1、在两个相似的五边形中,一个五边形各边长分别为1,2,3,4,5,另一个五边形最大边为10,则最短的边为( )(A)2 (B)4 (C)6 (D)82、如图所示的两个五边形相似,求未知边
的长度.A三、研读课文 知识点二 相似多边形性质的应用四、归纳小结 1、相似多边形的对应角_____,对应边的比______;反之,如果两个多边形的对应角_____,对应边的比 ___,那么这两个多边形______.
2、相似多边形____ 的比称为相似比.
3、学习反思:______________________________.相等对应边相等相等相等相似五、强化训练 1、△ABC与△DEF相似,且相似比是 ,
则△DEF与△ABC的相似比是( ).
A. B. C. D.2、已知2a-3b=0,b≠0,则a∶b=_____.B五、强化训练 3、已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?五、强化训练 4、如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EFAB相似,求EF的长.五、强化训练 Thank you!谢谢同学们的努力!
第一课时 27.1 图形的相似(1)一、新课引入 1、让同学们观察国徽上的五角星及教师准备
好的同底版不同尺寸的相片等等.
2、这些形状相同的图形之间,在数量关系和
位置关系上有什么规律吗?怎样才能按要求
放大和缩小一张美丽的相片?进入这一章学习吧,在实验,探究和论证之后,你会得出答案的。二、学习目标 从生活中形状相同的图形的实例
中认识图形的相似,理解相似图形
的概念.三、研读课文 认真阅读课本本章的内容,
完成下面练习并体验知识点的形
成过程.三、研读课文 知识点一:
相似图形的定义下图中,有用同一张底片洗出的不同
尺寸的照片,也有大小不同的足球,
还有一辆汽车和的模型.所有这些都给
我们一形状相同的形象,我们把这种
____________的图形叫做相似图形.形状相同三、研读课文 知识点一:
相似图形的定义
你能再举出相似图形的例子吗?三、研读课文 知识点一:
相似图形的定义
练一练
1、如图,图形a~f中,哪些是与
图形(1)或(2)相似的?答:与图(1)相似的有d与图(2)相似的有e三、研读课文 2、观察下列图形,指出哪些
是相似图形:答:是相似图形的有(1)与(8),
(2)与(6)知识点一:
相似图形的定义
三、研读课文 知识点二:相似图形
的来源两个图形相似,其中一个图形可以
看做是由另一个图形_________或
_________得到的,实际的建筑物
和它的模型是___________的,用
复印机把一个图形放大或缩小后所
得的图形,也是与原来的图
_________的.相似相似放大缩小三、研读课文 知识点二:相似图形
的来源
练一练1、如图,从放大镜里看到的三角尺
和原来的三角尺相似吗? 答:相似三、研读课文 知识点二:相似图形
的来源
2、如图,下面右边的四个图形中,
与左边的图形相似的是( )A三、研读课文 知识点二:相似图形
的来源
观察
下图是人们从平面镜及哈哈镜里
看懂的不同镜像,它们相似吗?总结:第一个图的两个图形______,
第二个图与第三个图的镜子中的
图像已变形,所以_________.相似不相似四、归纳小结 1、形状 的图形叫相似形.
2、两个图形相似,其中一个图形可以
看作由另一个图形的 或
而得到的.
3、学习反思:________________
_________________
______________________.相同放大缩小五、强化训练 1、下列说法正确的是( )
A.小明上幼儿园时的照片和初中毕业
时的照片相似.
B.商店新买来的一副三角板是相似的.
C.所有的课本都是相似的.
D.国旗的五角星都是相似的.D五、强化训练 2、下列说法中,错误的是( )
(A)两个全等三角形一定是相似形
(B)两个等腰三角形一定相似
(C)两个等边三角形一定相似
(D)两个等腰直角三角形一定相似B五、强化训练 3、在下列各组图形:
①两个平行四边形;②两个圆;
③两个矩形;④均有一个内角是80°的两个等腰三角形;
⑤两个正五边形;
⑥均有一个内角是100°的两个
等腰三角形.
其中一定是相似图形的是
.(填序号)②, ⑤, ⑥五、强化训练 4、在比例尺是1:8000000的“中国政区”
地图上,量得福州与上海之间的距离
是7.5cm,那么福州与上海之间的实
际距离是多少?解:设福州与上海之间的的实际距离是Xcm,
依题意得:答:福州与上海之间的的实际距离
是60千米五、强化训练 5、AB两地的实际距离为2500m,
在一张平面图上的距离是5cm,
那么这张平面地图的比例尺是多少?解:依题意可知,2500m=250000cm
故这张平面地图的比例尺是
答:这张平面地图的比例尺是 .
第二课时
27.1 图形的相似(2)名人名言:决心就是力量,
信心就是成功。---列夫.托尔斯泰一、新课引入 上节课我们介绍了什么样的图形是相似图形?
这节课我们将介绍两个相似图形都有哪些主要特征.
会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进行有关的计算. 二、学习目标 三、研读课文 知识点一 认真阅读课本第36至38页的内容,完成下面练习并体验知识点的形成过程. 相似多边形的性质观察(1)图27.1-4(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?三、研读课文 知识点一 相似多边形的性质解:△A1B1C1和△ABC相似
=====思考?(2)对于图27.1-4(2)中两个相似的正
六边形,是否也能得到类似的结论?是的三、研读课文
探究知识点一 相似多边形的性质如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形. 对于图中两个相似的四边形,它们
的对应角,对应边的比是否相等? (相等)问题三、研读课文 知识点一 相似多边形的性质结论: (1)相似多边形的特征:相似多边形的对应角______,对应边的比_______.
反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
相等相等相等相等相似 在⊿ABC和⊿A1B1C1中,
若 ,
则⊿ABC和⊿A1B1C1相似.
几何语言三、研读课文 知识点一 相似多边形的性质结论: (2)相似比:相似多边形________的比
称为相似比.
相似比为1时,相似的两个图形
______,
因此________形是一种特殊的相似形.
对应边全等全等三、研读课文 知识点一 相似多边形的性质(3)比例线段:对于四条线段 如果
与 相等
(如 ),(即___________)
我们就说这四条线段是成比例线段,简称
__________其中两条线段的比(即它们长度的比)另两条线段的比比例线段结论:三、研读课文 知识点一 相似多边形的性质 解:如图所示的两个直角三角形相似。
因为从图形标出的数据可看出这两个三角形
是等腰直角三角形,所以它们的对应角相等,对应边的比也相等,都等于1:2。 练一练:1、如图所示的两个直角
三角形相似吗?为什么?2、已知a、b、c、d是成比例线段,其中
a=2,b=5,c=3,则d=_____.7.5三、研读课文
知识点二 相似多边形性质的应用例 如图,四边形ABCD和EFGH相似,
求角 , 的大小和EH的长度 .三、研读课文
知识点二 相似多边形性质的应用三、研读课文
知识点二 相似多边形性质的应用练一练:1、在两个相似的五边形中,一个五边形各边长分别为1,2,3,4,5,另一个五边形最大边为10,则最短的边为( )(A)2 (B)4 (C)6 (D)82、如图所示的两个五边形相似,求未知边
的长度.A三、研读课文 知识点二 相似多边形性质的应用四、归纳小结 1、相似多边形的对应角_____,对应边的比______;反之,如果两个多边形的对应角_____,对应边的比 ___,那么这两个多边形______.
2、相似多边形____ 的比称为相似比.
3、学习反思:______________________________.相等对应边相等相等相等相似五、强化训练 1、△ABC与△DEF相似,且相似比是 ,
则△DEF与△ABC的相似比是( ).
A. B. C. D.2、已知2a-3b=0,b≠0,则a∶b=_____.B五、强化训练 3、已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?五、强化训练 4、如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EFAB相似,求EF的长.五、强化训练 Thank you!谢谢同学们的努力!
