物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞 课件(共53张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞 课件(共53张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-01 00:00:00 | ||
图片预览










文档简介
(共53张PPT)
第一章 动量守恒定律
第5节 弹性碰撞和非弹性碰撞
目录
主题(二) 完全非弹性碰撞
主题(一) 碰撞的种类
第5节 弹性碰撞和非弹性碰撞
主题(三) 弹性碰撞
碰撞给生活带来巨大的危害
所以我们要研究碰撞
新课引入
碰撞给生活带来巨大的乐趣
所以我们要研究碰撞
新课引入
第一部分
碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
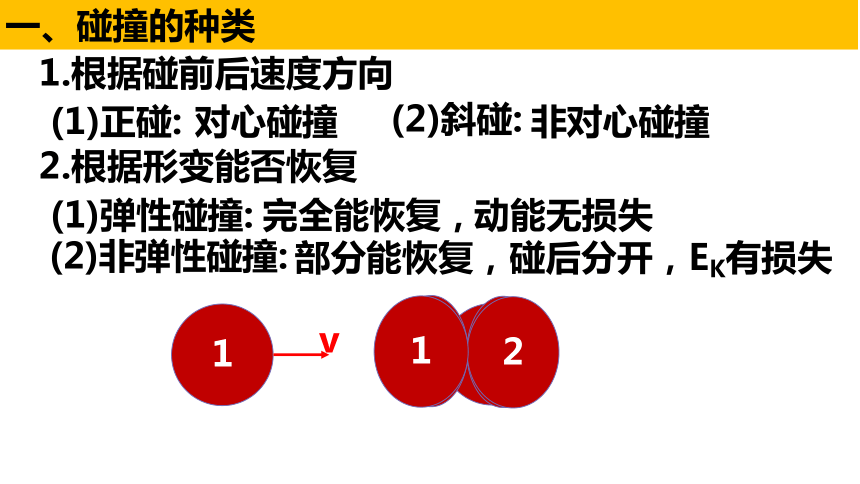
一、碰撞的种类
乒乓球
铁球
v
乒乓球
v
橡皮泥球
v
铁球
铁球
铁球和乒乓球的形变能恢复
橡皮泥球的形变不能恢复
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
2.根据形变能否恢复
(1)弹性碰撞:
1
2
v
2
1
2
1
v
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
(2)非弹性碰撞:
部分能恢复,碰后分开,EK有损失
1
2
v
2
1
2
1
2.根据形变能否恢复
(1)弹性碰撞:
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
(3)完全非弹性碰撞:
完全不恢复沾一起,
1
2
2
1
(2)非弹性碰撞:
部分能恢复,碰后分开,EK有损失
2.根据形变能否恢复
(1)弹性碰撞:
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
Ek损失最多
第二部分
完全非弹性碰撞
()2
1
2
v1
v2
1
2
v共
碰后连一起
2.规律:
1.特点:
动量守恒、
EK损失最多
并联质量
相对速度
二、完全非弹性碰撞
m1v1+m2v2
=(m1+m2)v共
得v共=
m1v12+m2v22-(m1+m2)v共2
EK损=
()2
1
2
v1
v2
1
2
v共
碰后连一起
2.规律:
1.特点:
动量守恒、
EK损失最多
注意:矢量方程v1、v2要考虑方向
并联质量
相对速度
二、完全非弹性碰撞
m1v1+m2v2
=(m1+m2)v共
得v共=
m1v12+m2v22-(m1+m2)v共2
EK损=
EK损=
) 2
m
M
V0
思考1:小物体什么时候到达最高点 如何求这个高度H
V共
H
思考2:小物体什么时候到达最高点 如何求这个高度H
V共
H
V0
m1
m2
mv0+0
=(m+M)v共
mv02-(m+M)v共2
EK损=
EK损=
()2
=mgH
m2v0+0
=(m1+m2)v共
m2v02-(m1+m2)v共2
EK损=
EK损=
()2
=m2gH
思考3:弹性势能什么时候到达最大 如何求这个EPm
m
m
V0
V共
思考4:木块木板共速后,如何求摩擦生的热Q
m
V共
ΔS
mv0+0
=(m+m)v共
mv02-(m+m)v共2
EK损=
EK损=
()2
=mgH
mv0+0
=(m+M)v共
mv02-(m+M)v共2
EK损=
EK损=
()2
=Q
=FfΔS
m
M
V0
V共
H
V共
H
V0
m
M
m
m
V0
V共
V共
V0
m
V共
m
V0
二、完全非弹性碰撞
3.模型全集
M
R
m
V0
m
M
V0
V0
V共
V共
H
V0
m
M
m
m
V0
V共
V共
V0
m
V共
m
V0
二、完全非弹性碰撞
3.模型全集
M
R
m
V0
m
M
V0
V0
V共
①木块斜槽模型
②轻绳模型
③弹簧模型
④木块木板模型
⑤子弹木板模型
【典例1】如图所示,光滑悬空轨道上静止一质量为3m的小车A,用一段不可伸长的轻质细绳悬挂一质量为2m的木块B.一质量为m的子弹以水平速度v0射入木块(时间极短),在以后的运动过程中,细绳离开竖直方向的最大角度小于90°,(不计空气阻力,重力加速度为g。试求:(1)子弹射入木块B时产生的热量;(2)木块B能摆起的最大高度;
mv0+0
=(m+2m)v1
mv02-(m+m)v12
Q=
解(1)子弹、B动量守恒
(v0-0)2
mv02
(2)子弹、B、A动量守恒
(m+2m)v1=
(m+2m+3m)v2
3mgh=
3mv12-6mv22
3mgh=
(v1-0)2
得h=
第三部分
弹性碰撞
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
m1(v12-v1/2)=
m2(v2/2-v22)
m1(v1+v1/)(v1-v1/)=
m2(v2/+v2)(v2/-v2)
m1(v1-v1/)=
m2(v2/-v2)
v1+v1/=
v2/+v2
得v2/=
v1+v1/-v2
m1v1+m2v2=
m1v1/+m2(v1+v1/-v2)
得v2/=
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
【典例2】(多选)在光滑水平面上,一质量为3m,速度大小为v1的1球与质量为m的2球发生迎面弹性碰撞,B的速度大小为v2,求碰后两球的速度大小v1/和v2/( )A.v1/= B.v1/=
C.v2/= D.v2/=
1
2
v1
v2
BD
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
注意:矢量方程v1、v2要考虑方向
【典例3】在光滑水平面上,一质量为m,速度大小为v的A球与质量为3m静止的B球发生正碰,碰撞可能是弹性的,也可能是非弹性的,则碰后B球的速度大小可能是( )A.0.1v
B.0.25v
C.0.50v
D.1.0v
BC
非弹性:
mv=(m+3m)v共
得:v共=0.25v
弹性:
得:vB=
=0.5v
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
v1-v共=v共-v1/
v共-v2=v2/-v共
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v2/-v1/=
v2-v1
【典例4】两球A、B在光滑的水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )A.vA′=5 m/s,vB′=2.5 m/sB.vA′=2 m/s,vB′=4 m/sC.vA′=-4 m/s,vB′=7 m/sD.vA′=7 m/s,vB′=1.5 m/s
B
vA-vB≥vB′-vA′≥0
【典例5】(多选)质量为1 kg的小球以4 m/s的速度与质量为2 kg的静止小球正碰,关于碰后的速度v1’和v2’,可能正确的是( )
A.v1′=v2′= m/s
B.v1′=3 m/s,v2′=0.5 m/sC.v1′=1 m/s,v2′=3 m/s
D.v1′=-1 m/s,v2′=2.5 m/s
AD
v1-v2≥v2′-v1′≥0
m1v1+m2v2=1×4+0
=4
m1v1′+m2v2′=1×1+2×3
=8
所有碰撞必修满足两个条件:①动量守恒
②v1-v2≥v2′-v1′≥0
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
注意:一切碰撞必满足(1)动量守恒
(2)v1-v2≥v2′-v1′≥0
【典例6】甲、乙两球在水平光滑轨道上同方向运动,已知它们的动量分别是p1=5 kg·m/s,p2=7 kg·m/s,甲从后面追上乙并发生碰撞,碰后乙球的动量变为10 kg·m/s,则两球质量m1与m2间的关系可能是( )A.m1=m2
B.2m1=m2C.4m1=m2
D.6m1=m2
C
碰后甲球的动量P2/=
2 kg·m/s
由v1-v2≥v2′-v1′≥0得
0
得m1m2
m1m2
【典例7】(多选)如图所示,在光滑水平面上,有两个半径相等的小球A、B,质量分别为mA、mB。A向右运动过程中与静止的B发生正碰,碰后两球动量相同,则mA与mB的关系可能是( )A.mA=0.5mB
B.mA=2mBC.mA=3mB
D.mA=4mB
BC
非弹性:
mAv0=(mA+mB)v共
弹性:
vA=
mAv共=mBv共
得:mA=mB
vB=
mAvA=mBvB
得:mA=3mB
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v1/=
v2
v2/=
v1
三、弹性碰撞
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
v1/=
v2
v2/=
v1
④若m1>>m2, 且V2=0:
极轻球以重球速度2倍弹开
结论:极重球撞静止的极轻球,极重球速度几乎不变
三、弹性碰撞
得v1/=
得v2/=
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v1/=
v2
v2/=
v1
v1/≈
v1
v2/≈
2v1
v
2v
三、弹性碰撞
结论:极重球撞静止的极轻球,极重球速度几乎不变
极轻球以重球速度2倍弹开
⑤若m1<结论:极轻球撞静止的极重球,极轻球必以原速率反弹
极重球仍然静止。
三、弹性碰撞
得v1/=
得v2/=
④若m1>>m2, 且V2=0:
极轻球以重球速度2倍弹开。
结论:极重球撞静止的极轻球,极重球速度几乎不变
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
v1/=
v2/=
v1
v1/≈
v1
v2/≈
2v1
v1/≈
-v1
v2/≈
0
三、弹性碰撞
结论:极轻球撞静止的极重球,极轻球必以原速率反弹
极重球仍然静止。
m
M
V0
思考1:小物体到达最高点又返回底端的速度方向?
VM
Vm
思考2:木块m2什么时候达到最大速度 其值是多少?
m1
m2
V0
V共
m1
m2
V1
V2
mv0+0=
mvm+MvM
mv02=
mvm2+MvM2
vm=
-v0
m1v0=
m1v1+m2v2
m1v02=
m1v12+m2v22
v2=
-0
思考3:圆环什么时候到达最大速度?
H
V0
m2
m1
V2
V共
V共
V1
V共
H
V共
m
V0
思考2:木块m2什么时候达到最大速度 其值是多少?
m1
m2
V0
V共
m1
m2
V1
V2
m1v0=
m1v1+m2v2
m1v02=
m1v12+m2v22
v2=
-0
V0
做什么运动?
做什么运动?
V0
思考3:圆环什么时候到达最大速度?
H
V0
m2
m1
V2
V共
V共
V1
V共
H
V共
m
V0
做什么运动?
L
单向周期性运动。
单向周期性运动。
往复的周期性运动。
m
M
V0
三、弹性碰撞
4.模型全集
VM
Vm
m1
m2
V0
V共
m1
m2
V1
V2
V0
m2
m1
V2
V1
V0
H
V1
V2
V共
H
V共
V共
【典例8】如图所示,质量为4m的光滑物块a静止在光滑水平地面上,物块a左侧面为圆弧面且与水平地面相切,质量为m的滑块b以初速度v0向右运动滑上a,沿a左侧面上滑一段距离后又返回,最后滑离a,不计一切摩擦,滑块b从滑上a到滑离a的过程中,下列说法正确的是( )
A.滑块b沿a上升 的最大高度为
B.滑块a运动的最大速度为
C.滑块b沿a上升 的最大高度为
D.滑块a运动的最大速度为
B
【典例9】(多选)如图所示,在光滑水平地面上放有两个小球A和B,mA>mB,B球上固定了一轻质弹簧且始终处于弹性限度内,A球以速率v去碰静止的B球,下列说法正确的是( )
A.A球的最小速率为零
B.B球的最大速率为v
C.当弹簧压缩到最短时,B球的速率最大
D.两球的总动能的最小值为
BD
m
M
V0
VM
Vm
Vy
VM
Vm
H
V0
V共
V共
Vy
V共
V共
三、弹性碰撞
m
M
V0
4.模型全集
VM
Vm
H
V共
【典例10】一个质量为m的物块位于四分之一光滑圆弧的底端,圆弧位于光滑水平面上,质量M=4m,半径为0.5m,小物块以V0=5m/s的速度冲向圆弧,求(1)物体升高的最高距离hm,(2)物体滑回底端的速度
v共
vy
得hm=1m
hm
v共
v共
解(1)
mv0=(m+M)v共
mv02-(m+M)v共2
mghm=
(v0-0)2
得mghm=
【典例10】一个质量为m的物块位于四分之一光滑圆弧的底端,圆弧位于光滑水平面上,质量M=4m,半径为0.5m,小物块以V0=5m/s的速度冲向圆弧,求(1)物体升高的最高距离hm,(2)物体滑回底端的速度
得vm=
hm
v共
v共
解(2)
mv0=mvm+MvM
mvm2+MvM2
vm
vM
mv02=
-v0
=-3m/s
总结提升
第四部分
课堂小结
一、碰撞的种类
二、完全非弹性碰撞
1.根据碰前后速度方向
1.特点:
2.规律:
2.根据形变能否恢复
三、弹性碰撞
3.模型全集:
1.特点:
2.规律:
4.模型全集:
3.结论:
【练习1】质量相等的A、B两球在光滑水平面上沿同一条直线、在同一方向上运动,A球的动量pA=9 kg·m/s,B球的动量pB=3 kg·m/s。A球追上B球时发生碰撞,则A、B两球碰撞后的动量可能是( )
A.pA′=6 kg·m/s,pB′=6 kg·m/s
B.pA′=8 kg·m/s,pB′=4 kg·m/s
C.pA′=-2 kg·m/s,pB′=14 kg·m/s
D.pA′=-4 kg·m/s,pB′=17 kg·m/s
A
课堂练习
【练习2】(多选)质量分别为m1和m2的两个物块在光滑的水平面上发生正碰,碰撞时间极短,其x-t图像如图所示,则下列判断正确的是( )
A.两物块的质量之比m1:m2=1:3
B.两物块的质量之比m1:m2=1:2
C.两物块碰撞后粘在一起
D.此碰撞一定为弹性碰撞
典例分析
AD
课堂练习
【练习3】在光滑的水平面上有三个完全相同的小球,它们在同一条直线上,2、3小球静止,并靠在一起,1小球以速度v0射向它们,如图所示。设碰撞中不损失机械能,则碰后三个小球的速度可能值是( )
A.v1=v2=v3=v0
B.v1=0,v2=v3=v0
C.v1=0,v2=v3=v0
D.v1=v2=0,v3=v0
D
典例分析
课堂练习
【练习4】(多选)质量为M的带有光滑圆弧轨道的小车静止置于光滑水平面1上,如图所示,一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回小车的左端,则( )
A.小球以后将向左做平抛运动
B.小球将做自由落体运动
C.此过程小球对小车做的功为Mv02
D.小球在弧形轨道上升的最大高度为
BC
课堂练习
谢 谢 观 看
第一章 动量守恒定律
第5节 弹性碰撞和非弹性碰撞
目录
主题(二) 完全非弹性碰撞
主题(一) 碰撞的种类
第5节 弹性碰撞和非弹性碰撞
主题(三) 弹性碰撞
碰撞给生活带来巨大的危害
所以我们要研究碰撞
新课引入
碰撞给生活带来巨大的乐趣
所以我们要研究碰撞
新课引入
第一部分
碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
一、碰撞的种类
乒乓球
铁球
v
乒乓球
v
橡皮泥球
v
铁球
铁球
铁球和乒乓球的形变能恢复
橡皮泥球的形变不能恢复
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
2.根据形变能否恢复
(1)弹性碰撞:
1
2
v
2
1
2
1
v
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
(2)非弹性碰撞:
部分能恢复,碰后分开,EK有损失
1
2
v
2
1
2
1
2.根据形变能否恢复
(1)弹性碰撞:
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
(3)完全非弹性碰撞:
完全不恢复沾一起,
1
2
2
1
(2)非弹性碰撞:
部分能恢复,碰后分开,EK有损失
2.根据形变能否恢复
(1)弹性碰撞:
完全能恢复,
动能无损失
一、碰撞的种类
(1)正碰:
1.根据碰前后速度方向
(2)斜碰:
对心碰撞
非对心碰撞
Ek损失最多
第二部分
完全非弹性碰撞
()2
1
2
v1
v2
1
2
v共
碰后连一起
2.规律:
1.特点:
动量守恒、
EK损失最多
并联质量
相对速度
二、完全非弹性碰撞
m1v1+m2v2
=(m1+m2)v共
得v共=
m1v12+m2v22-(m1+m2)v共2
EK损=
()2
1
2
v1
v2
1
2
v共
碰后连一起
2.规律:
1.特点:
动量守恒、
EK损失最多
注意:矢量方程v1、v2要考虑方向
并联质量
相对速度
二、完全非弹性碰撞
m1v1+m2v2
=(m1+m2)v共
得v共=
m1v12+m2v22-(m1+m2)v共2
EK损=
EK损=
) 2
m
M
V0
思考1:小物体什么时候到达最高点 如何求这个高度H
V共
H
思考2:小物体什么时候到达最高点 如何求这个高度H
V共
H
V0
m1
m2
mv0+0
=(m+M)v共
mv02-(m+M)v共2
EK损=
EK损=
()2
=mgH
m2v0+0
=(m1+m2)v共
m2v02-(m1+m2)v共2
EK损=
EK损=
()2
=m2gH
思考3:弹性势能什么时候到达最大 如何求这个EPm
m
m
V0
V共
思考4:木块木板共速后,如何求摩擦生的热Q
m
V共
ΔS
mv0+0
=(m+m)v共
mv02-(m+m)v共2
EK损=
EK损=
()2
=mgH
mv0+0
=(m+M)v共
mv02-(m+M)v共2
EK损=
EK损=
()2
=Q
=FfΔS
m
M
V0
V共
H
V共
H
V0
m
M
m
m
V0
V共
V共
V0
m
V共
m
V0
二、完全非弹性碰撞
3.模型全集
M
R
m
V0
m
M
V0
V0
V共
V共
H
V0
m
M
m
m
V0
V共
V共
V0
m
V共
m
V0
二、完全非弹性碰撞
3.模型全集
M
R
m
V0
m
M
V0
V0
V共
①木块斜槽模型
②轻绳模型
③弹簧模型
④木块木板模型
⑤子弹木板模型
【典例1】如图所示,光滑悬空轨道上静止一质量为3m的小车A,用一段不可伸长的轻质细绳悬挂一质量为2m的木块B.一质量为m的子弹以水平速度v0射入木块(时间极短),在以后的运动过程中,细绳离开竖直方向的最大角度小于90°,(不计空气阻力,重力加速度为g。试求:(1)子弹射入木块B时产生的热量;(2)木块B能摆起的最大高度;
mv0+0
=(m+2m)v1
mv02-(m+m)v12
Q=
解(1)子弹、B动量守恒
(v0-0)2
mv02
(2)子弹、B、A动量守恒
(m+2m)v1=
(m+2m+3m)v2
3mgh=
3mv12-6mv22
3mgh=
(v1-0)2
得h=
第三部分
弹性碰撞
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
m1(v12-v1/2)=
m2(v2/2-v22)
m1(v1+v1/)(v1-v1/)=
m2(v2/+v2)(v2/-v2)
m1(v1-v1/)=
m2(v2/-v2)
v1+v1/=
v2/+v2
得v2/=
v1+v1/-v2
m1v1+m2v2=
m1v1/+m2(v1+v1/-v2)
得v2/=
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
【典例2】(多选)在光滑水平面上,一质量为3m,速度大小为v1的1球与质量为m的2球发生迎面弹性碰撞,B的速度大小为v2,求碰后两球的速度大小v1/和v2/( )A.v1/= B.v1/=
C.v2/= D.v2/=
1
2
v1
v2
BD
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
注意:矢量方程v1、v2要考虑方向
【典例3】在光滑水平面上,一质量为m,速度大小为v的A球与质量为3m静止的B球发生正碰,碰撞可能是弹性的,也可能是非弹性的,则碰后B球的速度大小可能是( )A.0.1v
B.0.25v
C.0.50v
D.1.0v
BC
非弹性:
mv=(m+3m)v共
得:v共=0.25v
弹性:
得:vB=
=0.5v
1
2
v1
v2
1
2
v1/
v2/
1
2
v共
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
v1-v共=v共-v1/
v共-v2=v2/-v共
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v2/-v1/=
v2-v1
【典例4】两球A、B在光滑的水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )A.vA′=5 m/s,vB′=2.5 m/sB.vA′=2 m/s,vB′=4 m/sC.vA′=-4 m/s,vB′=7 m/sD.vA′=7 m/s,vB′=1.5 m/s
B
vA-vB≥vB′-vA′≥0
【典例5】(多选)质量为1 kg的小球以4 m/s的速度与质量为2 kg的静止小球正碰,关于碰后的速度v1’和v2’,可能正确的是( )
A.v1′=v2′= m/s
B.v1′=3 m/s,v2′=0.5 m/sC.v1′=1 m/s,v2′=3 m/s
D.v1′=-1 m/s,v2′=2.5 m/s
AD
v1-v2≥v2′-v1′≥0
m1v1+m2v2=1×4+0
=4
m1v1′+m2v2′=1×1+2×3
=8
所有碰撞必修满足两个条件:①动量守恒
②v1-v2≥v2′-v1′≥0
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
注意:一切碰撞必满足(1)动量守恒
(2)v1-v2≥v2′-v1′≥0
【典例6】甲、乙两球在水平光滑轨道上同方向运动,已知它们的动量分别是p1=5 kg·m/s,p2=7 kg·m/s,甲从后面追上乙并发生碰撞,碰后乙球的动量变为10 kg·m/s,则两球质量m1与m2间的关系可能是( )A.m1=m2
B.2m1=m2C.4m1=m2
D.6m1=m2
C
碰后甲球的动量P2/=
2 kg·m/s
由v1-v2≥v2′-v1′≥0得
0
得m1m2
m1m2
【典例7】(多选)如图所示,在光滑水平面上,有两个半径相等的小球A、B,质量分别为mA、mB。A向右运动过程中与静止的B发生正碰,碰后两球动量相同,则mA与mB的关系可能是( )A.mA=0.5mB
B.mA=2mBC.mA=3mB
D.mA=4mB
BC
非弹性:
mAv0=(mA+mB)v共
弹性:
vA=
mAv共=mBv共
得:mA=mB
vB=
mAvA=mBvB
得:mA=3mB
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
1.特点:
形变能够完全恢复
(理想模型)
动量守恒、
2.规律:
动能守恒
三、弹性碰撞
m1v1+m2v2=
m1v1/+m2v2/
m1v12+m2v22=
m1v1/2+m2v2/2
得v1/=
得v2/=
3.结论:
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v1/=
v2
v2/=
v1
三、弹性碰撞
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
v1/=
v2
v2/=
v1
④若m1>>m2, 且V2=0:
极轻球以重球速度2倍弹开
结论:极重球撞静止的极轻球,极重球速度几乎不变
三、弹性碰撞
得v1/=
得v2/=
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
①在压缩和弹开阶段,每个球速度的变化量相等。
②弹性碰撞:相对接近速度=相对离开速度。
一切碰撞:相对接近速度≥相对离开速度≥0。
v1/=
v2
v2/=
v1
v1/≈
v1
v2/≈
2v1
v
2v
三、弹性碰撞
结论:极重球撞静止的极轻球,极重球速度几乎不变
极轻球以重球速度2倍弹开
⑤若m1<
极重球仍然静止。
三、弹性碰撞
得v1/=
得v2/=
④若m1>>m2, 且V2=0:
极轻球以重球速度2倍弹开。
结论:极重球撞静止的极轻球,极重球速度几乎不变
③若两球质量相等:
结论:弹性碰撞质量相等两球交换速度
v1/=
v2/=
v1
v1/≈
v1
v2/≈
2v1
v1/≈
-v1
v2/≈
0
三、弹性碰撞
结论:极轻球撞静止的极重球,极轻球必以原速率反弹
极重球仍然静止。
m
M
V0
思考1:小物体到达最高点又返回底端的速度方向?
VM
Vm
思考2:木块m2什么时候达到最大速度 其值是多少?
m1
m2
V0
V共
m1
m2
V1
V2
mv0+0=
mvm+MvM
mv02=
mvm2+MvM2
vm=
-v0
m1v0=
m1v1+m2v2
m1v02=
m1v12+m2v22
v2=
-0
思考3:圆环什么时候到达最大速度?
H
V0
m2
m1
V2
V共
V共
V1
V共
H
V共
m
V0
思考2:木块m2什么时候达到最大速度 其值是多少?
m1
m2
V0
V共
m1
m2
V1
V2
m1v0=
m1v1+m2v2
m1v02=
m1v12+m2v22
v2=
-0
V0
做什么运动?
做什么运动?
V0
思考3:圆环什么时候到达最大速度?
H
V0
m2
m1
V2
V共
V共
V1
V共
H
V共
m
V0
做什么运动?
L
单向周期性运动。
单向周期性运动。
往复的周期性运动。
m
M
V0
三、弹性碰撞
4.模型全集
VM
Vm
m1
m2
V0
V共
m1
m2
V1
V2
V0
m2
m1
V2
V1
V0
H
V1
V2
V共
H
V共
V共
【典例8】如图所示,质量为4m的光滑物块a静止在光滑水平地面上,物块a左侧面为圆弧面且与水平地面相切,质量为m的滑块b以初速度v0向右运动滑上a,沿a左侧面上滑一段距离后又返回,最后滑离a,不计一切摩擦,滑块b从滑上a到滑离a的过程中,下列说法正确的是( )
A.滑块b沿a上升 的最大高度为
B.滑块a运动的最大速度为
C.滑块b沿a上升 的最大高度为
D.滑块a运动的最大速度为
B
【典例9】(多选)如图所示,在光滑水平地面上放有两个小球A和B,mA>mB,B球上固定了一轻质弹簧且始终处于弹性限度内,A球以速率v去碰静止的B球,下列说法正确的是( )
A.A球的最小速率为零
B.B球的最大速率为v
C.当弹簧压缩到最短时,B球的速率最大
D.两球的总动能的最小值为
BD
m
M
V0
VM
Vm
Vy
VM
Vm
H
V0
V共
V共
Vy
V共
V共
三、弹性碰撞
m
M
V0
4.模型全集
VM
Vm
H
V共
【典例10】一个质量为m的物块位于四分之一光滑圆弧的底端,圆弧位于光滑水平面上,质量M=4m,半径为0.5m,小物块以V0=5m/s的速度冲向圆弧,求(1)物体升高的最高距离hm,(2)物体滑回底端的速度
v共
vy
得hm=1m
hm
v共
v共
解(1)
mv0=(m+M)v共
mv02-(m+M)v共2
mghm=
(v0-0)2
得mghm=
【典例10】一个质量为m的物块位于四分之一光滑圆弧的底端,圆弧位于光滑水平面上,质量M=4m,半径为0.5m,小物块以V0=5m/s的速度冲向圆弧,求(1)物体升高的最高距离hm,(2)物体滑回底端的速度
得vm=
hm
v共
v共
解(2)
mv0=mvm+MvM
mvm2+MvM2
vm
vM
mv02=
-v0
=-3m/s
总结提升
第四部分
课堂小结
一、碰撞的种类
二、完全非弹性碰撞
1.根据碰前后速度方向
1.特点:
2.规律:
2.根据形变能否恢复
三、弹性碰撞
3.模型全集:
1.特点:
2.规律:
4.模型全集:
3.结论:
【练习1】质量相等的A、B两球在光滑水平面上沿同一条直线、在同一方向上运动,A球的动量pA=9 kg·m/s,B球的动量pB=3 kg·m/s。A球追上B球时发生碰撞,则A、B两球碰撞后的动量可能是( )
A.pA′=6 kg·m/s,pB′=6 kg·m/s
B.pA′=8 kg·m/s,pB′=4 kg·m/s
C.pA′=-2 kg·m/s,pB′=14 kg·m/s
D.pA′=-4 kg·m/s,pB′=17 kg·m/s
A
课堂练习
【练习2】(多选)质量分别为m1和m2的两个物块在光滑的水平面上发生正碰,碰撞时间极短,其x-t图像如图所示,则下列判断正确的是( )
A.两物块的质量之比m1:m2=1:3
B.两物块的质量之比m1:m2=1:2
C.两物块碰撞后粘在一起
D.此碰撞一定为弹性碰撞
典例分析
AD
课堂练习
【练习3】在光滑的水平面上有三个完全相同的小球,它们在同一条直线上,2、3小球静止,并靠在一起,1小球以速度v0射向它们,如图所示。设碰撞中不损失机械能,则碰后三个小球的速度可能值是( )
A.v1=v2=v3=v0
B.v1=0,v2=v3=v0
C.v1=0,v2=v3=v0
D.v1=v2=0,v3=v0
D
典例分析
课堂练习
【练习4】(多选)质量为M的带有光滑圆弧轨道的小车静止置于光滑水平面1上,如图所示,一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回小车的左端,则( )
A.小球以后将向左做平抛运动
B.小球将做自由落体运动
C.此过程小球对小车做的功为Mv02
D.小球在弧形轨道上升的最大高度为
BC
课堂练习
谢 谢 观 看
