福建省莆田市锦江中学2023-2024学年高二下学期期中考试数学试题(含解析)
文档属性
| 名称 | 福建省莆田市锦江中学2023-2024学年高二下学期期中考试数学试题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-01 00:00:00 | ||
图片预览




文档简介
莆田锦江中学2023-2024学年(下)期中测试
数学试卷
一、单选题
1.已知随机变量服从正态分布,,则( )
A.0.7 B.0.6 C.0.4 D.0.2
2.已知变量与之间的一组数据如表:
2 4 5 6 8
30 50 70
若与的线性回归方程为,则的值为( )
A.60 B.70 C.100 D.110
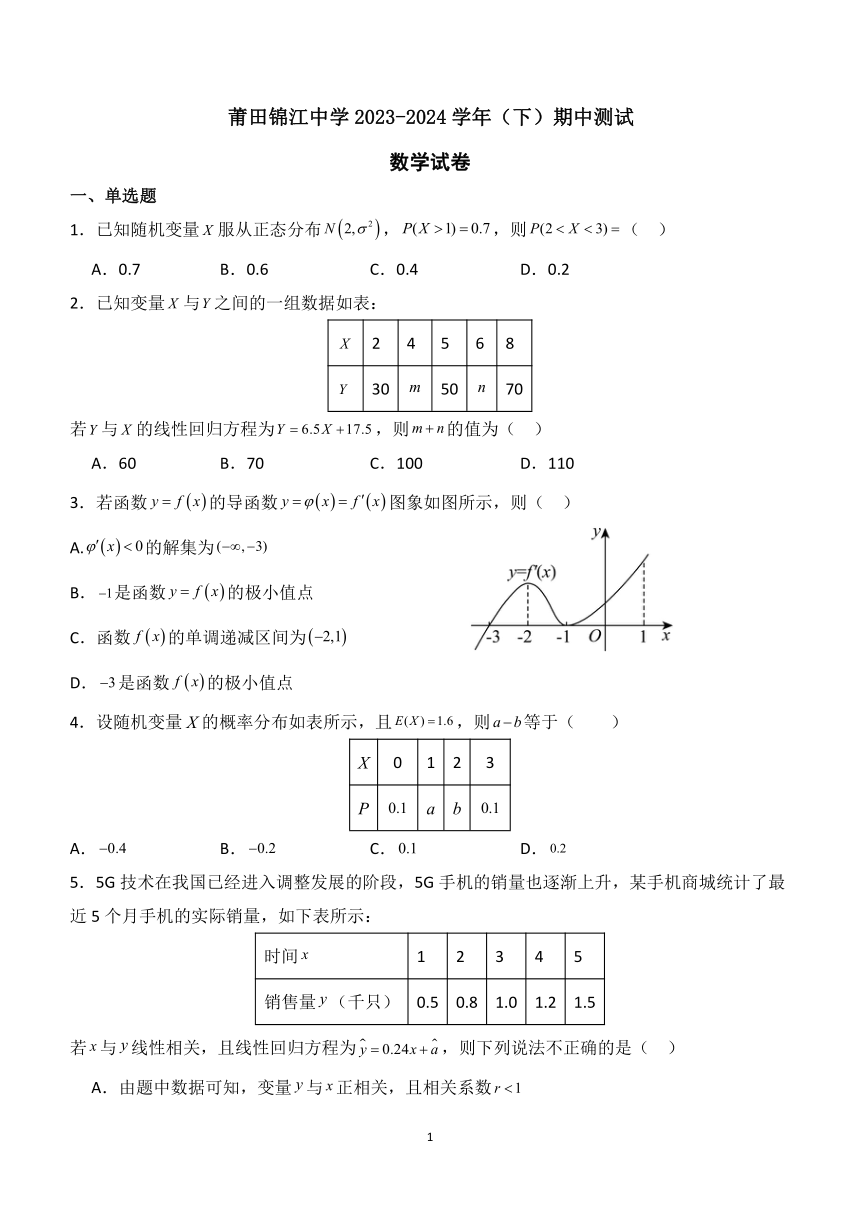
若函数的导函数图象如图所示,则( )
A.的解集为
B.是函数的极小值点
C.函数的单调递减区间为
D.是函数的极小值点
4.设随机变量X的概率分布如表所示,且,则等于( )
X 0 1 2 3
P a b
A. B. C. D.
5.5G技术在我国已经进入调整发展的阶段,5G手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:
时间 1 2 3 4 5
销售量(千只) 0.5 0.8 1.0 1.2 1.5
若与线性相关,且线性回归方程为,则下列说法不正确的是( )
A.由题中数据可知,变量与正相关,且相关系数
B.线性回归方程中
C.当解释变量每增加1个单位时,预报变量平均增加0.24个单位
D.可以预测时,该商场5G手机销量约为1.72(千只)
6.正方体中,是中点,则直线与线所成角的余弦值是( )
B.
C. D.
7.若函数有大于零的极值点,则实数a的取值范围为( )
A. B. C. D.
8.在棱长为的正方体中,,,分别为棱,,的中点,动点在平面内,且.则下列说法正确的是( )
A.存在点,使得直线与直线相交
B.存在点,使得直线平面
C.直线与平面所成角的大小为
D.平面被正方体所截得的截面面积为
二、多选题
9.(多选)下列结论正确的是( )
A.已知向量a=(9,4,-4),b=(1,2,2),则a在b上的投影向量为(1,2,2)
B.若对空间中任意一点O,有则P,A,B,C四点共面
C.已知{a,b,c}是空间的一组基底,若m=a+c,则{a,b,m}也是空间的一组基底
D.若直线l的方向向量为e=(1,0,3),平面α的法向量n=(-2,0,),则直线l⊥α
10.下列结论正确的是( )
A.若随机变量服从两点分布,,则
B.若随机变量的方差,则
C.若随机变量服从二项分布,则
D.若随机变量服正态分布,,则
11.已知函数,下列说法正确的有( )
A.当时,则在上单调递增
B.当时,函数有唯一极值点
C.若函数只有两个不等于1的零点,则必有
D.若函数有三个零点,则
三、填空题
12.曲线在点处的切线方程为 .
13.甲袋中有5个红球和3个白球,乙袋中有4个红球和2个白球,如果所有小球只存在颜色的差别,并且整个取球过程是盲取,分两步进行:第一步,先从甲袋中随机取出一球放入乙袋,分别用、表示由甲袋中取出红球、白球的事件;第二步,再从乙袋中随机取出两球,用B表示第二步由乙袋中取出的球是“两球都为红球”的事件,则事件B的概率是 .
14.人教A版选择性必修一习题1.4拓广探索第17题中提到“在空间直角坐标系中,己知向量,点,若平面经过点,且以为法向量,点是平面内的任意一点,则平面的方程为”.现己知平面的方程为,直线l是平面与平面的交线,且直线l的方向向量为,则平面的一个法向量可以为 ,直线l与平面所成角的正弦值为 .
四、解答题
15.已知曲线在点处的切线的斜率为1.
(1)求实数a的值;
(2)求函数的单调区间与极值.
16.软笔书法又称中国书法,是我国的国粹之一,琴棋书画中的“书”指的正是书法.作为我国的独有艺术,书法不仅能够陶冶情操,培养孩子对艺术的审美,还能开发孩子的智力,拓展孩子的思维与手的灵活性,对孩子的身心健康发展起着重要的作用.越来越多的家长开始注重孩子的书法教育,某书法培训机构统计了其招收的所有学生中每种软笔书法学习人数(每人只学习一种书体)的情况,得到相关统计数据如下:
书体 楷书 行书 草书 隶书 篆书
人数 24 16 10 20 10
(1)该培训机构统计了某周学习软笔书法学生的作业完成情况,得到下表:
认真完成 不认真完成 总计
男生 7 27
女生
总计 65
补全2×2列联表,并判断能否有的把握认为是否认真完成作业与性别有关;
(2)现从该培训机构学习楷书与行书的学生中,按学生学习的书体用分层抽样的方法抽取10人,再从这10人中随机抽取4人,记4人中学习行书的人数为X,求X的分布列及数学期望.
参考公式及数据:.
0.25 0.15 0.10
1.323 2.072 2.706
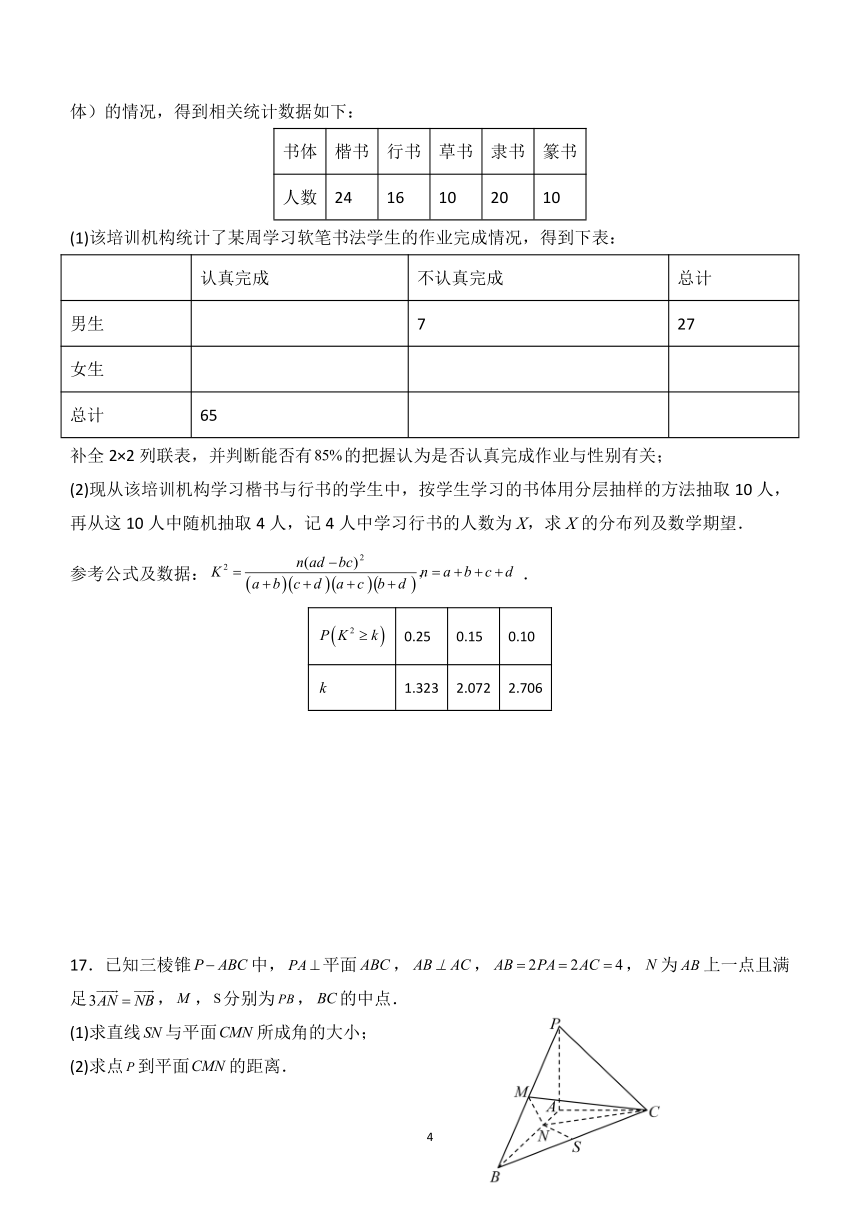
17.已知三棱锥中,平面,,,为上一点且满足,,分别为,的中点.
(1)求直线与平面所成角的大小;
(2)求点到平面的距离.
18.盒中有大小颜色相同的6个乒乓球,其中4个未使用过(称之为新球),2个使用过(称之为旧球).每局比赛从盒中随机取2个球作为比赛用球,该局比赛结束后放回盒中. 使用过的球即成为旧球.
(1)求一局比赛后盒中恰有3个新球的概率;
(2)设两局比赛后盒中新球的个数为,求的分布列.
19.已知函数.
(1)求函数在点处的切线方程;
(2)若对于任意,都有恒成立,求实数的取值范围.
参考答案:
1.D
【详解】因为,则,
∴.
2.C
【详解】因为,又与的线性回归方程为,
所以,即,解得.
3.D
【详解】对于A,由图可知,的解集即函数的单调递减区间,为,故A错误;
对于B,由图,的左右两边,所以不是函数的极值点,故B错误;
对于C,由图当时,所以的单调递减区间为,故C错误;
对于D,由图当时,单调递减,当时,,单调递增,
所以是函数的极小值点,故D正确.
4.B
【详解】由题意得,,
解得,
故.
5.B
【详解】从数据看随的增加而增加,故变量与正相关,由于各增量并不相等,故相关系数,故A正确;
由已知数据得,,
代入中得到,故B错;
根据线性回归方程可得每增加一个单位时,预报变量平均增加0.24个单位,故C正确.
将代入中得到,故D正确.
6.A
【详解】依题意建立空间直角坐标系,如图,
不妨设,则,
故,
所以,
所以直线与线所成角的余弦值为.
7.C
【详解】函数,
可得,
若,此时单调递增,无极值点,
故,令,解得,
当时,,当时,,
故是的极值点
由于函数有大于零的极值点,
,解得.
8.C
【详解】
连接,,所以,,取的中点,连接,
所以,点到线段的最短距离大于,所以不存在点,使得直线与直线相交,故不正确;
以为坐标原点,分别以,,所在直线为轴,轴,轴建立空间直角坐标系,则,,,,
所以,,,
设平面的法向量为,所以,即,
令,则,,所以,
所以点到平面的距离为,而,所以不存在点,使得直线平面,故不正确;
因为,所以平面,连接交于点,所以为的中点,,
所以为直线与平面所成角,
因为,在中,,
所以,因为与全等,所以,故正确;
延长交的延长线于,连接交于,连接,取的中点,的中点,
连接,,,,,,
平面被正方体所截得的截面图形为正六边形,且边长为,
所以截面面积为,故不正确.
9.ABC
【详解】因为a=(9,4,-4),b=(1,2,2),所以a在b上的投影向量为·=·b=·(1,2,2)=(1,2,2),故A正确;因为++=1,故B正确;{a,b,c}是空间的一组基底,m=a+c,所以{a,b,a+c}两向量之间不共线,所以{a,b,m}也是空间的一组基底,故C正确;因为直线l的方向向量为e=(1,0,3),平面α的法向量n=(-2,0,),e·n=-2+0+2=0,则直线l∥α或l α,故D错误.
10.CD
【详解】对于A,若随机变量服从两点分布,,
则,故A错误;
对于B,若随机变量的方差,则,故B错误;
对于C,若随机变量服从二项分布,
则,故C正确;
对于D,若随机变量服正态分布,,
则,故D正确.
11.ACD
【详解】对于A:当时,,
则,令,
则,
则当时,,单调递减,
当时,,单调递增,
故,所以在上单调递增,A正确;
对于B:当时,,
则,令,
则,
则当时,,单调递减,
当时,,单调递增,
故,所以在上单调递增,无极值,B错误;
对于C:令,得,
令,则,
令,则,
所以在上单调递减,又,
所以当时,,单调递增,且,
当时,,单调递减,且,
若函数只有两个不等于的零点,即函数与有两个交点,
则不妨取,
当时,,
所以函数与的两个交点横坐标互为倒数,即,C正确;
对于D:明显,所以是函数的一个零点,且,
函数有三个零点,且函数在上为连续函数,则函数必有两个极值点(不为1),
因为,
所以,
设,则
当时,令,得,单调递减,
,得,单调递增,
所以,所以在上单调递减,不可能有3个零点,
所以,令,得,单调递减,
,得,单调递增,
所以,
所以,所以,D正确.
12.
【详解】因为,则,
所以切点为,且,
则,
由直线的点斜式可得,化简可得,
所以切线方程为.
故答案为:
13.
【详解】
因为,
所以,
14. /
【详解】显然平面的一个法向量可以为,
易知平面的法向量为,平面的法向量为,
且直线l的方向向量为,故,,令,
解得,,故,设直线l与平面所成角为,
则.
15.(1)1
(2)递减区间为,递增区间为;极小值为,极大值为.
【详解】(1)由,得,
曲线在点处的切线的斜率为1,
故;
(2)由(1)知,,
令,则或;
令,则;
故函数的单调递减区间为,单调递增区间为;
故函数的极小值为,极大值为.
16.(1)表格见解析,没有
(2)分布列见解析,
【详解】(1)补全的列联表如下:
认真完成 不认真完成 总计
男生 20 7 27
女生 45 8 53
总计 65 15 80
则,
因为,
所以没有的把握认为是否认真完成作业与性别有关.
(2)因为学习楷书与行书的人数之比为.
所以抽取的10人中,学习楷书的有6人,学习行书的有4人.
所以的所有可能取值为.
,
,
.
所以的分布列为
0 1 2 3 4
所以.
17.(1)
(2)
【详解】(1)因为平面,,
如图以为原点,所在直线分别为轴 轴 轴,建立空间直角坐标系,
则,
所以,
因为,
所以.
(2)设平面的法向量,,
则,即,取,得,
设直线与平面所成角为,
则,又,
所以,所以直线与平面所成角的大小为.
(3)设点到平面的距离为,因为,
所以,所以点到平面的距离为.
18.(1);
(2)分布列见解析.
【详解】(1)因一局比赛后盒中恰有3个新球,则本局比赛取到了一个旧球,一个新球.
因一共有6个球,则总情况数为,取到一个新球,一个旧球的情况数为,
则相应概率为: ;
(2)设第一局取到两个旧球为事件,取到新旧两个球为,取到两个新球为,
第二局取到两个旧球为事件,取到新旧两个球为,取到两个新球为,
则两局比赛后新球的个数可能为0,1,2,3,4.
;
;
;
;
.
则分布列如下:
0 1 2 3 4
19.(1)
(2)
【详解】(1)由于,故,切点为,
,
所以切线的斜率为0,在点处的切线方程为.
(2)令,则,
所以为R上单调递增函数,
因为,所以时,时,,
所以在单调递减,在单调递增.
若对于任意,都有恒成立,即只需.
因为在单调递减,在单调递增,
所以的最大值为和中最大的一个,
所以,
设,
当时,,当时,,
所以在单调递减,在单调递增.
,故当时,.
当时,,则成立.
当时,由的单调性,得,即,不符合题意.
当时,,即,也不符合题意.
综上,的取值范围为.
数学试卷
一、单选题
1.已知随机变量服从正态分布,,则( )
A.0.7 B.0.6 C.0.4 D.0.2
2.已知变量与之间的一组数据如表:
2 4 5 6 8
30 50 70
若与的线性回归方程为,则的值为( )
A.60 B.70 C.100 D.110
若函数的导函数图象如图所示,则( )
A.的解集为
B.是函数的极小值点
C.函数的单调递减区间为
D.是函数的极小值点
4.设随机变量X的概率分布如表所示,且,则等于( )
X 0 1 2 3
P a b
A. B. C. D.
5.5G技术在我国已经进入调整发展的阶段,5G手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:
时间 1 2 3 4 5
销售量(千只) 0.5 0.8 1.0 1.2 1.5
若与线性相关,且线性回归方程为,则下列说法不正确的是( )
A.由题中数据可知,变量与正相关,且相关系数
B.线性回归方程中
C.当解释变量每增加1个单位时,预报变量平均增加0.24个单位
D.可以预测时,该商场5G手机销量约为1.72(千只)
6.正方体中,是中点,则直线与线所成角的余弦值是( )
B.
C. D.
7.若函数有大于零的极值点,则实数a的取值范围为( )
A. B. C. D.
8.在棱长为的正方体中,,,分别为棱,,的中点,动点在平面内,且.则下列说法正确的是( )
A.存在点,使得直线与直线相交
B.存在点,使得直线平面
C.直线与平面所成角的大小为
D.平面被正方体所截得的截面面积为
二、多选题
9.(多选)下列结论正确的是( )
A.已知向量a=(9,4,-4),b=(1,2,2),则a在b上的投影向量为(1,2,2)
B.若对空间中任意一点O,有则P,A,B,C四点共面
C.已知{a,b,c}是空间的一组基底,若m=a+c,则{a,b,m}也是空间的一组基底
D.若直线l的方向向量为e=(1,0,3),平面α的法向量n=(-2,0,),则直线l⊥α
10.下列结论正确的是( )
A.若随机变量服从两点分布,,则
B.若随机变量的方差,则
C.若随机变量服从二项分布,则
D.若随机变量服正态分布,,则
11.已知函数,下列说法正确的有( )
A.当时,则在上单调递增
B.当时,函数有唯一极值点
C.若函数只有两个不等于1的零点,则必有
D.若函数有三个零点,则
三、填空题
12.曲线在点处的切线方程为 .
13.甲袋中有5个红球和3个白球,乙袋中有4个红球和2个白球,如果所有小球只存在颜色的差别,并且整个取球过程是盲取,分两步进行:第一步,先从甲袋中随机取出一球放入乙袋,分别用、表示由甲袋中取出红球、白球的事件;第二步,再从乙袋中随机取出两球,用B表示第二步由乙袋中取出的球是“两球都为红球”的事件,则事件B的概率是 .
14.人教A版选择性必修一习题1.4拓广探索第17题中提到“在空间直角坐标系中,己知向量,点,若平面经过点,且以为法向量,点是平面内的任意一点,则平面的方程为”.现己知平面的方程为,直线l是平面与平面的交线,且直线l的方向向量为,则平面的一个法向量可以为 ,直线l与平面所成角的正弦值为 .
四、解答题
15.已知曲线在点处的切线的斜率为1.
(1)求实数a的值;
(2)求函数的单调区间与极值.
16.软笔书法又称中国书法,是我国的国粹之一,琴棋书画中的“书”指的正是书法.作为我国的独有艺术,书法不仅能够陶冶情操,培养孩子对艺术的审美,还能开发孩子的智力,拓展孩子的思维与手的灵活性,对孩子的身心健康发展起着重要的作用.越来越多的家长开始注重孩子的书法教育,某书法培训机构统计了其招收的所有学生中每种软笔书法学习人数(每人只学习一种书体)的情况,得到相关统计数据如下:
书体 楷书 行书 草书 隶书 篆书
人数 24 16 10 20 10
(1)该培训机构统计了某周学习软笔书法学生的作业完成情况,得到下表:
认真完成 不认真完成 总计
男生 7 27
女生
总计 65
补全2×2列联表,并判断能否有的把握认为是否认真完成作业与性别有关;
(2)现从该培训机构学习楷书与行书的学生中,按学生学习的书体用分层抽样的方法抽取10人,再从这10人中随机抽取4人,记4人中学习行书的人数为X,求X的分布列及数学期望.
参考公式及数据:.
0.25 0.15 0.10
1.323 2.072 2.706
17.已知三棱锥中,平面,,,为上一点且满足,,分别为,的中点.
(1)求直线与平面所成角的大小;
(2)求点到平面的距离.
18.盒中有大小颜色相同的6个乒乓球,其中4个未使用过(称之为新球),2个使用过(称之为旧球).每局比赛从盒中随机取2个球作为比赛用球,该局比赛结束后放回盒中. 使用过的球即成为旧球.
(1)求一局比赛后盒中恰有3个新球的概率;
(2)设两局比赛后盒中新球的个数为,求的分布列.
19.已知函数.
(1)求函数在点处的切线方程;
(2)若对于任意,都有恒成立,求实数的取值范围.
参考答案:
1.D
【详解】因为,则,
∴.
2.C
【详解】因为,又与的线性回归方程为,
所以,即,解得.
3.D
【详解】对于A,由图可知,的解集即函数的单调递减区间,为,故A错误;
对于B,由图,的左右两边,所以不是函数的极值点,故B错误;
对于C,由图当时,所以的单调递减区间为,故C错误;
对于D,由图当时,单调递减,当时,,单调递增,
所以是函数的极小值点,故D正确.
4.B
【详解】由题意得,,
解得,
故.
5.B
【详解】从数据看随的增加而增加,故变量与正相关,由于各增量并不相等,故相关系数,故A正确;
由已知数据得,,
代入中得到,故B错;
根据线性回归方程可得每增加一个单位时,预报变量平均增加0.24个单位,故C正确.
将代入中得到,故D正确.
6.A
【详解】依题意建立空间直角坐标系,如图,
不妨设,则,
故,
所以,
所以直线与线所成角的余弦值为.
7.C
【详解】函数,
可得,
若,此时单调递增,无极值点,
故,令,解得,
当时,,当时,,
故是的极值点
由于函数有大于零的极值点,
,解得.
8.C
【详解】
连接,,所以,,取的中点,连接,
所以,点到线段的最短距离大于,所以不存在点,使得直线与直线相交,故不正确;
以为坐标原点,分别以,,所在直线为轴,轴,轴建立空间直角坐标系,则,,,,
所以,,,
设平面的法向量为,所以,即,
令,则,,所以,
所以点到平面的距离为,而,所以不存在点,使得直线平面,故不正确;
因为,所以平面,连接交于点,所以为的中点,,
所以为直线与平面所成角,
因为,在中,,
所以,因为与全等,所以,故正确;
延长交的延长线于,连接交于,连接,取的中点,的中点,
连接,,,,,,
平面被正方体所截得的截面图形为正六边形,且边长为,
所以截面面积为,故不正确.
9.ABC
【详解】因为a=(9,4,-4),b=(1,2,2),所以a在b上的投影向量为·=·b=·(1,2,2)=(1,2,2),故A正确;因为++=1,故B正确;{a,b,c}是空间的一组基底,m=a+c,所以{a,b,a+c}两向量之间不共线,所以{a,b,m}也是空间的一组基底,故C正确;因为直线l的方向向量为e=(1,0,3),平面α的法向量n=(-2,0,),e·n=-2+0+2=0,则直线l∥α或l α,故D错误.
10.CD
【详解】对于A,若随机变量服从两点分布,,
则,故A错误;
对于B,若随机变量的方差,则,故B错误;
对于C,若随机变量服从二项分布,
则,故C正确;
对于D,若随机变量服正态分布,,
则,故D正确.
11.ACD
【详解】对于A:当时,,
则,令,
则,
则当时,,单调递减,
当时,,单调递增,
故,所以在上单调递增,A正确;
对于B:当时,,
则,令,
则,
则当时,,单调递减,
当时,,单调递增,
故,所以在上单调递增,无极值,B错误;
对于C:令,得,
令,则,
令,则,
所以在上单调递减,又,
所以当时,,单调递增,且,
当时,,单调递减,且,
若函数只有两个不等于的零点,即函数与有两个交点,
则不妨取,
当时,,
所以函数与的两个交点横坐标互为倒数,即,C正确;
对于D:明显,所以是函数的一个零点,且,
函数有三个零点,且函数在上为连续函数,则函数必有两个极值点(不为1),
因为,
所以,
设,则
当时,令,得,单调递减,
,得,单调递增,
所以,所以在上单调递减,不可能有3个零点,
所以,令,得,单调递减,
,得,单调递增,
所以,
所以,所以,D正确.
12.
【详解】因为,则,
所以切点为,且,
则,
由直线的点斜式可得,化简可得,
所以切线方程为.
故答案为:
13.
【详解】
因为,
所以,
14. /
【详解】显然平面的一个法向量可以为,
易知平面的法向量为,平面的法向量为,
且直线l的方向向量为,故,,令,
解得,,故,设直线l与平面所成角为,
则.
15.(1)1
(2)递减区间为,递增区间为;极小值为,极大值为.
【详解】(1)由,得,
曲线在点处的切线的斜率为1,
故;
(2)由(1)知,,
令,则或;
令,则;
故函数的单调递减区间为,单调递增区间为;
故函数的极小值为,极大值为.
16.(1)表格见解析,没有
(2)分布列见解析,
【详解】(1)补全的列联表如下:
认真完成 不认真完成 总计
男生 20 7 27
女生 45 8 53
总计 65 15 80
则,
因为,
所以没有的把握认为是否认真完成作业与性别有关.
(2)因为学习楷书与行书的人数之比为.
所以抽取的10人中,学习楷书的有6人,学习行书的有4人.
所以的所有可能取值为.
,
,
.
所以的分布列为
0 1 2 3 4
所以.
17.(1)
(2)
【详解】(1)因为平面,,
如图以为原点,所在直线分别为轴 轴 轴,建立空间直角坐标系,
则,
所以,
因为,
所以.
(2)设平面的法向量,,
则,即,取,得,
设直线与平面所成角为,
则,又,
所以,所以直线与平面所成角的大小为.
(3)设点到平面的距离为,因为,
所以,所以点到平面的距离为.
18.(1);
(2)分布列见解析.
【详解】(1)因一局比赛后盒中恰有3个新球,则本局比赛取到了一个旧球,一个新球.
因一共有6个球,则总情况数为,取到一个新球,一个旧球的情况数为,
则相应概率为: ;
(2)设第一局取到两个旧球为事件,取到新旧两个球为,取到两个新球为,
第二局取到两个旧球为事件,取到新旧两个球为,取到两个新球为,
则两局比赛后新球的个数可能为0,1,2,3,4.
;
;
;
;
.
则分布列如下:
0 1 2 3 4
19.(1)
(2)
【详解】(1)由于,故,切点为,
,
所以切线的斜率为0,在点处的切线方程为.
(2)令,则,
所以为R上单调递增函数,
因为,所以时,时,,
所以在单调递减,在单调递增.
若对于任意,都有恒成立,即只需.
因为在单调递减,在单调递增,
所以的最大值为和中最大的一个,
所以,
设,
当时,,当时,,
所以在单调递减,在单调递增.
,故当时,.
当时,,则成立.
当时,由的单调性,得,即,不符合题意.
当时,,即,也不符合题意.
综上,的取值范围为.
同课章节目录
