五年级下册数学苏教版分数的意义与性质课件(共68张PPT)
文档属性
| 名称 | 五年级下册数学苏教版分数的意义与性质课件(共68张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-01 17:13:37 | ||
图片预览











文档简介
(共68张PPT)
分数的意义与性质
开启分数复习之旅
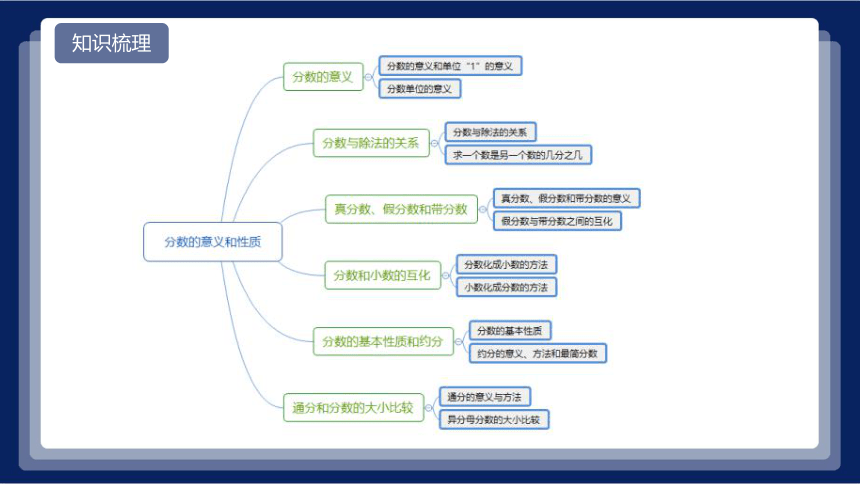
知识梳理
1.分数的意义
知识梳理
(1)一个物体、一个计量单位或者由许多物体组成的一个整体,
都可以用自然数1来表示,通常我们把它叫单位“1”。
(2)把单位“1”平均分成若干份,表示这样的一份或几份的数,叫作分数。
(3)把单位“1”平均分成若干份,表示其中一份的数,叫作分数单位。
(4)一个分数,分母是几,分数单位就是几分之一;分子是几,就有几个这样的分数单位。
易错题1
判断:把一个西瓜分给5个小朋友,每个小朋友分得这个西瓜的 。( )
易错题2
填空:把3张饼平均分成5份,每份是3张饼的( )。
易错题3
选择:不同的分数,分数单位( )
A.一定不同 B.一定相同 C.可能相同
不同的分数,分数单位( )
一定不同
一定相同
可能相同
易错题4
艾迪从一楼走到六楼,每上一层楼的时间相等。艾迪上一层楼的时间是上楼总时间的几分之几?
易错题5
一块西红柿地的 与一块黄瓜地的 相比,哪个面积大?
难题精选1
有16本练习本, 平均分给4名同学。每本练习本是练习本总数的 ,每位同学分得的练习本是练习本总数的 。
难题精选2
的意义是把( )平均分成( )份,取其中的( )份,分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
难题精选3
在分数里,分母表示( )
A.分数单位 B.取的份数 C.把单位“1”平均分成的份数
难题精选4
判断:分数单位是 的分数有4个。( )
难题精选5
把一根3米长的木料锯成5段,每锯一次所用的时间相等。锯2次所用的时间占所用总时间的几分之几?锯3次所用的时间占所用总时间的几分之几?
难题精选6
用分数表示图中的涂色部分。
( )
( )
2.分数与除法的关系
知识梳理
(1)分数与除法的关系:被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线,商相当于分数值,即
用字母表示为
(2)求一个数是另一个数的几分之几的实际问题的解法:一个数÷另一个数
即问A是B的几分之几,用A÷B,A是比较量,B是标准量;
易错题1
判断:除法中的被除数就是分数的分子,除数就是分数的分母,除号就是分数线。( )
易错题2
判断:1千克的 小于3千克的 。( )
易错题3
两根同样长的绳子,第一根用去 米,第二根用去这根绳子的 ,则( )
A.第一根用去得多
B.第二根用去得多
C.用去的一样多
D.无法判断
易错题4
判断:把一张正方形纸连续对折4次后展开,其中的3份是这张纸的 。( )
难题精选1
米可以理解为把1米看作单位“1”,平均分成( )份,有这样的( )份;还可以理解为把( )米看作单位“1”,平均分成( )份,有这样的( )份。
难题精选2
把一根8米长的绳子平均分成5份,每份的长度是8米的( ),每份的长度是( )米。
难题精选3
一辆汽车4分钟行驶3千米,平均每分钟行驶( )千米,平均每行驶1千米用( )分钟。
难题精选4
有同样大小的红、黑、白三种颜色的珠子共86个,按1个红珠子、3个白珠子、2个黑珠子的顺序依次排列。三种颜色的珠子各占珠子总数的几分之几?
难题精选5
在括号里填上适当的分数。
7时=( )日
9克=( )千克
31厘米=( )米
190毫升=( )升
31分=( )时
15平方分米=( )平方米
难题精选6
一袋水果糖共2千克,把这袋水果糖平均分给3个小朋友,每个小朋友分得几分之几千克?每个小朋友分得这袋水果糖的几分之几?
难题精选7
经过某十字路口的汽车,可能继续直行,也可能向左转或向右转。如果这三种情况出现的可能性相同,那么两辆汽车经过这个十字路口全部继续直行的可能性是几分之几?至少有一辆汽车向右转的可能性是几分之几?
3.真分数、假分数和带分数
知识梳理
(1)分子比分母小的分数叫作真分数,真分数小于1。
(2)分子比分母大或者分子和分母相等的分数叫作假分数,
假分数大于或等于1。
(3)分子是分母倍数的假分数可以化成整数。
(4)分子不是分母倍数的假分数,可以写成整数和真分数合成的数。这样的假分数通常叫作带分数。(注意:带分数是假分数的另一种表示形式)
(5)假分数化带分数的方法:1、借助图示转化;2、根据假分数的意义进行推想;3、根据分数与除法的关系计算——直接用分子除以分母,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。
(6)带分数化假分数的方法:分母不变,分子=分母×整数部分+真分数的分子
易错题1
判断:分数分为真分数、假分数和带分数三类。( )
易错题2
选择:分子是9的假分数有( )个。
A.9个 B.8个 C.无数
易错题3
x是非零自然数,要使 是真分数, 是假分数,
x可以是_______
难题精选1
分母是5的真分数有( ),
分子是5的假分数有( )
难题精选2
判断:
假分数都比1大。 ( )
分母是7的假分数有7个。 ( )
有一块菜地,其中的 种番茄, 种黄瓜,还有 种辣椒。 ( )
假分数都能化成带分数。 ( )
分数都小于整数。 ( )
难题精选3
一个分数,分子与分母的和是28,如果分子减去2,这个分数就等于1,原分数是多少?
难题精选4
有一个分数是 (为非零自然数),
当x=( )时,这个分数是最小的假分数;
当x=( )时,这个分数是最大的真分数;
当x=( )时,这个分数可以化成最小的带分数。
难题精选5
一个带分数,它的分数部分的分子是5,把它化成假分数后分子是19,这个带分数是多少?
难题精选6
找规律:1、 、 、 、……这组数中,第8个是多少?
4.分数和小数的互化
知识梳理
(1)把分数化成小数,直接用分数的分子除以分母,除不尽的保留相应位数的小数。
(2)小数可以看作分数的另一种表示形式。把小数化成分数,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子。
易错题1
把下面的分数化成小数。
难题精选1
填一填:
, 里最大能填数字( )
, 里最大能填数字( )
难题精选2
按要求填数
5.分数的基本性质和约分
知识梳理
(1)分数的基本性质:分数的分子和分母同时乘或除以
一个相同的数(0除外),分数的大小不变。
(2)一个分数的分母不变,分子扩大到原来的几倍,这个分数就扩大到原来的几倍;一个分数的分子不变,分母缩小到原来的几分之一,这个分数反而扩大到原来的几倍。
(3)约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫作约分.
(4)约分的方法:(1)分步约分法:用分子和分母的公因数(1除外)逐次分别去除分子、分母,得出最简分数.(2)一次约分法:直接用分子和分母的最大公因数分别去除分子、分母,得出最简分数.用最大公因数进行一次约分比较简便.
(5)最简分数:分子、分母只有公因数1,像这样的分数叫作最简分数.
易错题1
判断:分数的分子和分母同时乘或除以同一个数,分数的大小不变。( )
易错题2
判断:小于 而大于 的最简分数只有 。( )
易错题3
判断:最简分数的分子与分母没有公因数。( )
易错题4
填空:
难题精选1
一个分数,先用3约分一次,再用5约分一次后得 ,
这个分数原来是多少?
难题精选2
一个分数,分子与分母的和是56,约分后得 ,
这个分数原来是多少?
难题精选3
一个分数,分母比分子大15,分数值与 相等,
这个分数是多少?
难题精选4
的分子加上一个数,分母减去同一个数,所得的新分数约分后得 ,这个数是多少?
难题精选5
的分子、分母同时减去同一个数得到一个新分数,新分数约分后是 ,减去的这个数是多少?
6.通分和分数的大小比较
知识梳理
(1)通分的意义:把几个分母不同的分数(也叫作异分母分数)
分别化成和原来分数相等的同分母分数,叫作通分.
相同的分母叫作这几个分数的公分母.
(2)通分的方法:通分时,一般用原来几个分母的最小公倍数作公分母,
然后把各分数分别化成用这个公分母作分母的分数.
(3)异分母分数比较大小最常用的三个方法:
通分、分子变相同、化小数
此外还可以用画图比较,或者找基准数(1、 )进行比较
易错题1
判断:通分时,必须用分母的最小公倍数作公分母 ( )
易错题2
判断:通分时,分数变大;约分时,分数变小 ( )
易错题3
判断:通分时,分数的分子和分母都扩大了,分数值也随之扩大了 ( )
易错题4
判断:同分子分数比较大小,分母越大,分数值越大 ( )
难题精选1
两个分数 和 在通分后,分别化成 和 ,
则( )
A. c=a+b B. a=bc C. b=ac D. c=ab
难题精选2
一个最简分数,分子加上一个数,这个分数就等于 ,分子减去同一个数,这个分数就等于 ,这个最简分数是多少?
难题精选3
已知a、b是两个非零自然数, ,且a、b的和是20,
求a和b分别是多少
闯关成功
分数的意义与性质
开启分数复习之旅
知识梳理
1.分数的意义
知识梳理
(1)一个物体、一个计量单位或者由许多物体组成的一个整体,
都可以用自然数1来表示,通常我们把它叫单位“1”。
(2)把单位“1”平均分成若干份,表示这样的一份或几份的数,叫作分数。
(3)把单位“1”平均分成若干份,表示其中一份的数,叫作分数单位。
(4)一个分数,分母是几,分数单位就是几分之一;分子是几,就有几个这样的分数单位。
易错题1
判断:把一个西瓜分给5个小朋友,每个小朋友分得这个西瓜的 。( )
易错题2
填空:把3张饼平均分成5份,每份是3张饼的( )。
易错题3
选择:不同的分数,分数单位( )
A.一定不同 B.一定相同 C.可能相同
不同的分数,分数单位( )
一定不同
一定相同
可能相同
易错题4
艾迪从一楼走到六楼,每上一层楼的时间相等。艾迪上一层楼的时间是上楼总时间的几分之几?
易错题5
一块西红柿地的 与一块黄瓜地的 相比,哪个面积大?
难题精选1
有16本练习本, 平均分给4名同学。每本练习本是练习本总数的 ,每位同学分得的练习本是练习本总数的 。
难题精选2
的意义是把( )平均分成( )份,取其中的( )份,分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
难题精选3
在分数里,分母表示( )
A.分数单位 B.取的份数 C.把单位“1”平均分成的份数
难题精选4
判断:分数单位是 的分数有4个。( )
难题精选5
把一根3米长的木料锯成5段,每锯一次所用的时间相等。锯2次所用的时间占所用总时间的几分之几?锯3次所用的时间占所用总时间的几分之几?
难题精选6
用分数表示图中的涂色部分。
( )
( )
2.分数与除法的关系
知识梳理
(1)分数与除法的关系:被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线,商相当于分数值,即
用字母表示为
(2)求一个数是另一个数的几分之几的实际问题的解法:一个数÷另一个数
即问A是B的几分之几,用A÷B,A是比较量,B是标准量;
易错题1
判断:除法中的被除数就是分数的分子,除数就是分数的分母,除号就是分数线。( )
易错题2
判断:1千克的 小于3千克的 。( )
易错题3
两根同样长的绳子,第一根用去 米,第二根用去这根绳子的 ,则( )
A.第一根用去得多
B.第二根用去得多
C.用去的一样多
D.无法判断
易错题4
判断:把一张正方形纸连续对折4次后展开,其中的3份是这张纸的 。( )
难题精选1
米可以理解为把1米看作单位“1”,平均分成( )份,有这样的( )份;还可以理解为把( )米看作单位“1”,平均分成( )份,有这样的( )份。
难题精选2
把一根8米长的绳子平均分成5份,每份的长度是8米的( ),每份的长度是( )米。
难题精选3
一辆汽车4分钟行驶3千米,平均每分钟行驶( )千米,平均每行驶1千米用( )分钟。
难题精选4
有同样大小的红、黑、白三种颜色的珠子共86个,按1个红珠子、3个白珠子、2个黑珠子的顺序依次排列。三种颜色的珠子各占珠子总数的几分之几?
难题精选5
在括号里填上适当的分数。
7时=( )日
9克=( )千克
31厘米=( )米
190毫升=( )升
31分=( )时
15平方分米=( )平方米
难题精选6
一袋水果糖共2千克,把这袋水果糖平均分给3个小朋友,每个小朋友分得几分之几千克?每个小朋友分得这袋水果糖的几分之几?
难题精选7
经过某十字路口的汽车,可能继续直行,也可能向左转或向右转。如果这三种情况出现的可能性相同,那么两辆汽车经过这个十字路口全部继续直行的可能性是几分之几?至少有一辆汽车向右转的可能性是几分之几?
3.真分数、假分数和带分数
知识梳理
(1)分子比分母小的分数叫作真分数,真分数小于1。
(2)分子比分母大或者分子和分母相等的分数叫作假分数,
假分数大于或等于1。
(3)分子是分母倍数的假分数可以化成整数。
(4)分子不是分母倍数的假分数,可以写成整数和真分数合成的数。这样的假分数通常叫作带分数。(注意:带分数是假分数的另一种表示形式)
(5)假分数化带分数的方法:1、借助图示转化;2、根据假分数的意义进行推想;3、根据分数与除法的关系计算——直接用分子除以分母,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。
(6)带分数化假分数的方法:分母不变,分子=分母×整数部分+真分数的分子
易错题1
判断:分数分为真分数、假分数和带分数三类。( )
易错题2
选择:分子是9的假分数有( )个。
A.9个 B.8个 C.无数
易错题3
x是非零自然数,要使 是真分数, 是假分数,
x可以是_______
难题精选1
分母是5的真分数有( ),
分子是5的假分数有( )
难题精选2
判断:
假分数都比1大。 ( )
分母是7的假分数有7个。 ( )
有一块菜地,其中的 种番茄, 种黄瓜,还有 种辣椒。 ( )
假分数都能化成带分数。 ( )
分数都小于整数。 ( )
难题精选3
一个分数,分子与分母的和是28,如果分子减去2,这个分数就等于1,原分数是多少?
难题精选4
有一个分数是 (为非零自然数),
当x=( )时,这个分数是最小的假分数;
当x=( )时,这个分数是最大的真分数;
当x=( )时,这个分数可以化成最小的带分数。
难题精选5
一个带分数,它的分数部分的分子是5,把它化成假分数后分子是19,这个带分数是多少?
难题精选6
找规律:1、 、 、 、……这组数中,第8个是多少?
4.分数和小数的互化
知识梳理
(1)把分数化成小数,直接用分数的分子除以分母,除不尽的保留相应位数的小数。
(2)小数可以看作分数的另一种表示形式。把小数化成分数,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子。
易错题1
把下面的分数化成小数。
难题精选1
填一填:
, 里最大能填数字( )
, 里最大能填数字( )
难题精选2
按要求填数
5.分数的基本性质和约分
知识梳理
(1)分数的基本性质:分数的分子和分母同时乘或除以
一个相同的数(0除外),分数的大小不变。
(2)一个分数的分母不变,分子扩大到原来的几倍,这个分数就扩大到原来的几倍;一个分数的分子不变,分母缩小到原来的几分之一,这个分数反而扩大到原来的几倍。
(3)约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫作约分.
(4)约分的方法:(1)分步约分法:用分子和分母的公因数(1除外)逐次分别去除分子、分母,得出最简分数.(2)一次约分法:直接用分子和分母的最大公因数分别去除分子、分母,得出最简分数.用最大公因数进行一次约分比较简便.
(5)最简分数:分子、分母只有公因数1,像这样的分数叫作最简分数.
易错题1
判断:分数的分子和分母同时乘或除以同一个数,分数的大小不变。( )
易错题2
判断:小于 而大于 的最简分数只有 。( )
易错题3
判断:最简分数的分子与分母没有公因数。( )
易错题4
填空:
难题精选1
一个分数,先用3约分一次,再用5约分一次后得 ,
这个分数原来是多少?
难题精选2
一个分数,分子与分母的和是56,约分后得 ,
这个分数原来是多少?
难题精选3
一个分数,分母比分子大15,分数值与 相等,
这个分数是多少?
难题精选4
的分子加上一个数,分母减去同一个数,所得的新分数约分后得 ,这个数是多少?
难题精选5
的分子、分母同时减去同一个数得到一个新分数,新分数约分后是 ,减去的这个数是多少?
6.通分和分数的大小比较
知识梳理
(1)通分的意义:把几个分母不同的分数(也叫作异分母分数)
分别化成和原来分数相等的同分母分数,叫作通分.
相同的分母叫作这几个分数的公分母.
(2)通分的方法:通分时,一般用原来几个分母的最小公倍数作公分母,
然后把各分数分别化成用这个公分母作分母的分数.
(3)异分母分数比较大小最常用的三个方法:
通分、分子变相同、化小数
此外还可以用画图比较,或者找基准数(1、 )进行比较
易错题1
判断:通分时,必须用分母的最小公倍数作公分母 ( )
易错题2
判断:通分时,分数变大;约分时,分数变小 ( )
易错题3
判断:通分时,分数的分子和分母都扩大了,分数值也随之扩大了 ( )
易错题4
判断:同分子分数比较大小,分母越大,分数值越大 ( )
难题精选1
两个分数 和 在通分后,分别化成 和 ,
则( )
A. c=a+b B. a=bc C. b=ac D. c=ab
难题精选2
一个最简分数,分子加上一个数,这个分数就等于 ,分子减去同一个数,这个分数就等于 ,这个最简分数是多少?
难题精选3
已知a、b是两个非零自然数, ,且a、b的和是20,
求a和b分别是多少
闯关成功
