六年级下册数学人教版 《反比例 》课件(共32张PPT)
文档属性
| 名称 | 六年级下册数学人教版 《反比例 》课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 46.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-01 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
第2课时 反比例
表示x和y成正比例的关系式是( )
A x+y=12
B y=
C
直径一定,圆周长与圆周率成正比例关系。
6=x×y
一
复习导入
(2)圆的周长和半径。
(3)一袋大米的重量一定,吃了的和剩下的。
(1)三角形的高一定,面积和底。
1. 判断下面各题中的两种量是否成正比例关系。
学习目标
1.通过感知生活中的事例,理解并掌握反比例的意义。
2.判断两种相关联的量是否成反比例。
二
探究新知
2
反比例
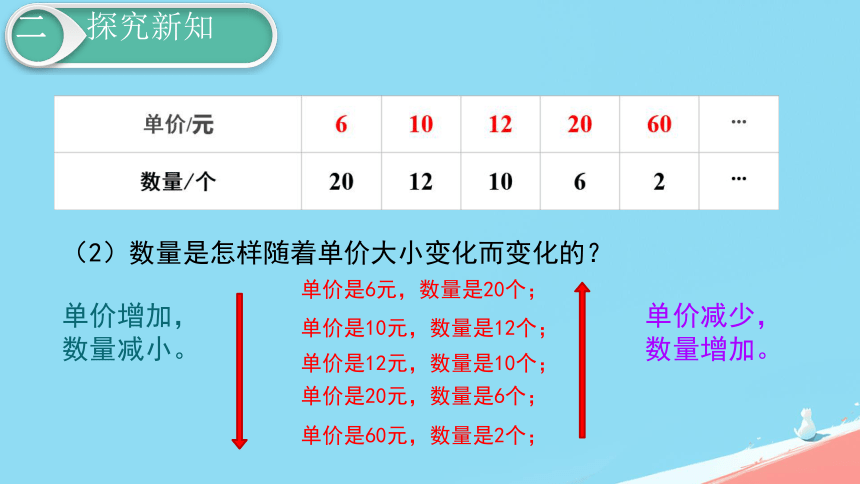
变形金刚的单价与个数变化情况如下表。
6
20
10
12
12
10
20
6
60
2
…
…
我有120元钱。
二
探究新知
观察上表,回答下面的问题。
(1)表中有哪两种量?
二
探究新知
(2)数量是怎样随着单价大小变化而变化的?
单价增加,
数量减小。
单价是6元,数量是20个;
单价是10元,数量是12个;
单价是12元,数量是10个;
单价是20元,数量是6个;
单价是60元,数量是2个;
单价减少,
数量增加。
二
探究新知
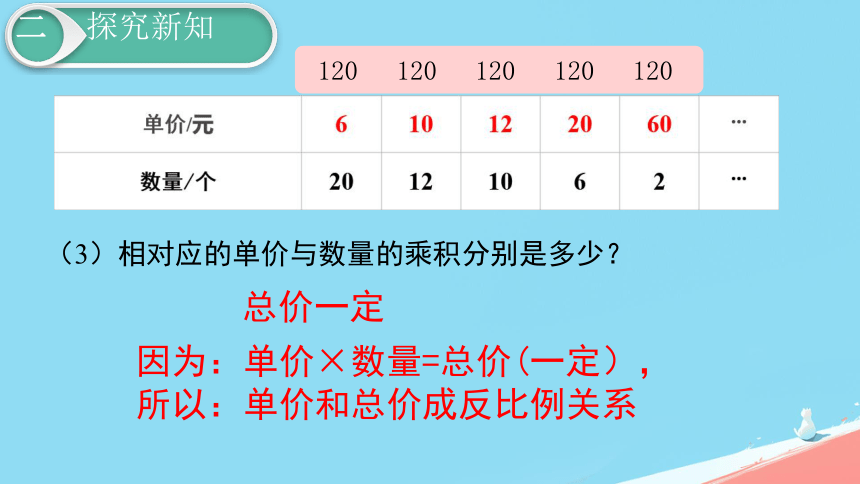
(3)相对应的单价与数量的乘积分别是多少?
总价一定
因为:单价×数量=总价(一定),
所以:单价和总价成反比例关系
120
120
120
120
120
二
探究新知
1.像这样两种相关联的量,一种量变化,另一种量也随着变化。
2.这两种量中相对应的两个数的乘积一定。
3.这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
(一定)
三
对应练习
做一做
优翼
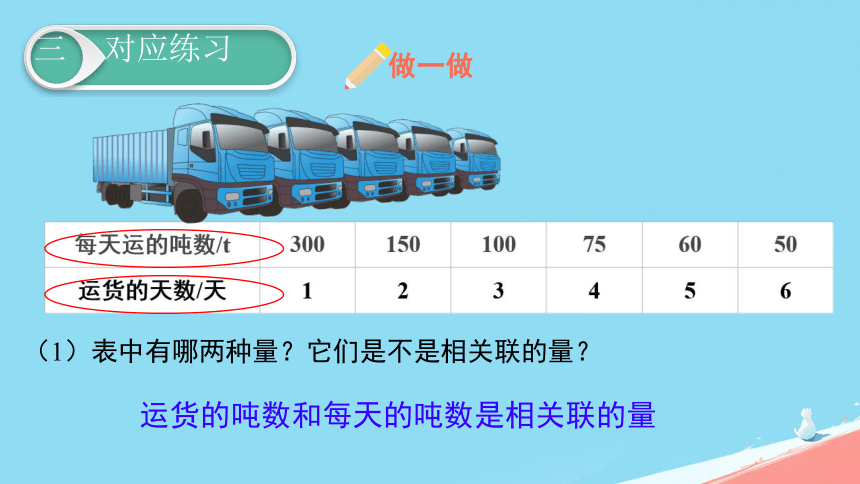
(1)表中有哪两种量?它们是不是相关联的量?
运货的吨数和每天的吨数是相关联的量
三
对应练习
做一做
优翼
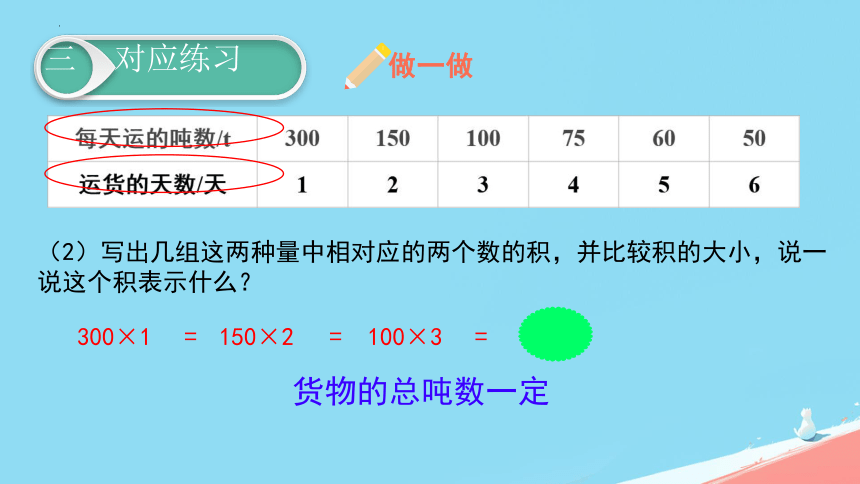
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
300×1
150×2
100×3
=
=
=
300
货物的总吨数一定
三
对应练习
做一做
优翼
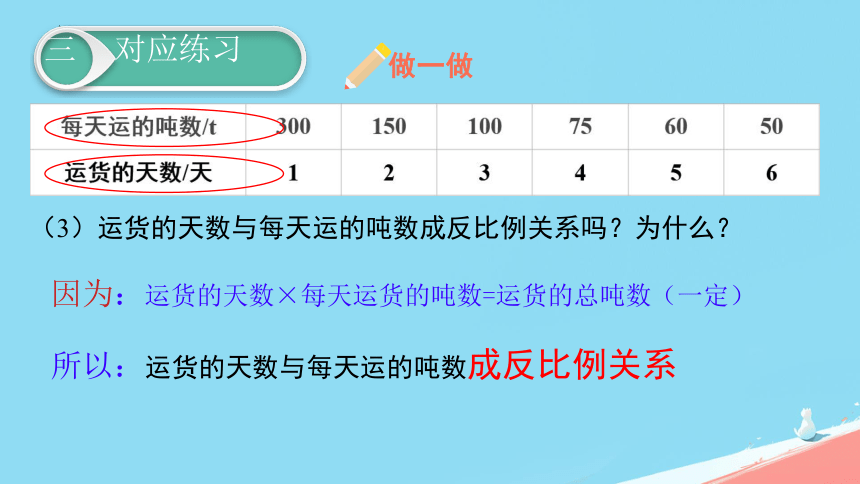
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
因为:运货的天数×每天运货的吨数=运货的总吨数(一定)
所以:运货的天数与每天运的吨数成反比例关系
二
探究新知
如果长方形的面积一定,长与宽成反比例关系。
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
区别判断正比例和反比例的方法:
正比例:两个相关联的量,比值一定。
反比例:两个相关联的量,乘积一定。
五
巩固练习
(1)分子一定,分母和分数值成反比例。
(2)2×5=10,所以2和5成反比例。
(3)三角形面积一定,底和高成反比例。
1.判断对错,并说说为什么。
×
( )
√
( )
( )
√
A B
√
×
分母×分数值=分子(一定)
4.煤的数量一定,使用天数与每天的平均用煤量。
A B
√
×
使用天数×每天的平均用煤量=煤的总吨数(一定)
5.全班人数一定,按各组人数相等的要求分组,组数与每组的人数。
组数×每组的人数=总人数(一定)
6.在一块菜地上种的黄瓜与西红柿的面积。
不成反比例,因为种黄瓜的面积+西红柿的面积=总面积
四
课堂小结
两种相关联的量,一种量的变化,另一种量也随着变化,这两种量中相对的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系,用字母表示为:
x y=k
(一定)
2.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
因为:地砖数×每块地砖的面积=教室总面积(一定)
所以:所需地砖数量与每块地砖的面积成反比例关系
900×600=540000(cm )=54(m )
1800×300=540000(cm )=54(m )
3600×150=540000(cm )=54(m )
3.食品加工厂准备把一批新酿的醋装瓶运往商店。
所装瓶数与每瓶容量是否成反比例关系?为什么?
因为:每瓶容量×所装瓶数=醋的体积(一定)。
所以:所装瓶数与每瓶容量成反比例关系。
250×1200=300000(ml)=300(L)
500×600=300000(ml)=300(L)
750×400=300000(ml)=300(L)
6.在一块菜地上种的黄瓜与西红柿的面积。
不成反比例,因为种黄瓜的面积+西红柿的面积=总面积
7.书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
成反比例,因为每包的册数×包数=书的总册数(一定)
六
拓展练习
P52T15
优翼
1.有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成 比例关系。
(2)当x一定时,z与y成 比例关系。
(3)当y一定时,z与x成 比例关系。
反
正
正
0
12. 一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装手机总数之间的关系吗?
(2)p与t成什么比例关系?
(1)答:手机总数=pt
(2)答:p、t成反比例关系。
练习九
0
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
500×24÷8=1500(部)
答:每天组装1500部手机。
练习九
五
巩固练习
4.下表中x和y两个量成反比例关系,请把表格填写完整。
50
100
0.25
12
P51T10
优翼
六
拓展练习
P52T16
优翼
2.一个长方形的面积是36cm2,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
y与x成反比例关系,图象不是一条直线。
0
4. 已知y与x成正比例关系,在下表的空格中填写合适的数。
5
12.5
25
50
3
8
15
练习九
0
13. 京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
(1)京沪高铁全长多少千米?
260×5=1300(千米)
答:京沪高铁全长1300千米。
练习九
0
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
答:t与v成反比例。关系式:tv=1300。
1300÷325=4(小时)
答:驶完全程需要4小时。
练习九
0
13. 京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
(1)京沪高铁全长多少千米?
260×5=1300(千米)
答:京沪高铁全长1300千米。
练习九
0
14. 右面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑得快还是长颈鹿跑的快?
答:斑马和长颈鹿的奔跑路程和奔跑时间都成正比例关系。
答:从图象中可知斑马18分钟大约跑22km,长颈鹿18分钟大约跑14km。
答:从图象上看,斑马跑的快。
练习九
0
16*. 一个长方形的面积是36cm ,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
答:长方形的面积=长×宽,xy=36,y与x的乘积一定,所以y与x成方比例关系。
列举数据:
x/cm
y/cm
9
12
18
36
4
3
2
1
0
4
8
12
16
20
24
28
32
36
x/cm
4
8
12
16
20
24
28
32
36
y/cm
所以xy=36的图象不是一条直线,而是一条曲线。
练习九
第2课时 反比例
表示x和y成正比例的关系式是( )
A x+y=12
B y=
C
直径一定,圆周长与圆周率成正比例关系。
6=x×y
一
复习导入
(2)圆的周长和半径。
(3)一袋大米的重量一定,吃了的和剩下的。
(1)三角形的高一定,面积和底。
1. 判断下面各题中的两种量是否成正比例关系。
学习目标
1.通过感知生活中的事例,理解并掌握反比例的意义。
2.判断两种相关联的量是否成反比例。
二
探究新知
2
反比例
变形金刚的单价与个数变化情况如下表。
6
20
10
12
12
10
20
6
60
2
…
…
我有120元钱。
二
探究新知
观察上表,回答下面的问题。
(1)表中有哪两种量?
二
探究新知
(2)数量是怎样随着单价大小变化而变化的?
单价增加,
数量减小。
单价是6元,数量是20个;
单价是10元,数量是12个;
单价是12元,数量是10个;
单价是20元,数量是6个;
单价是60元,数量是2个;
单价减少,
数量增加。
二
探究新知
(3)相对应的单价与数量的乘积分别是多少?
总价一定
因为:单价×数量=总价(一定),
所以:单价和总价成反比例关系
120
120
120
120
120
二
探究新知
1.像这样两种相关联的量,一种量变化,另一种量也随着变化。
2.这两种量中相对应的两个数的乘积一定。
3.这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
(一定)
三
对应练习
做一做
优翼
(1)表中有哪两种量?它们是不是相关联的量?
运货的吨数和每天的吨数是相关联的量
三
对应练习
做一做
优翼
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
300×1
150×2
100×3
=
=
=
300
货物的总吨数一定
三
对应练习
做一做
优翼
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
因为:运货的天数×每天运货的吨数=运货的总吨数(一定)
所以:运货的天数与每天运的吨数成反比例关系
二
探究新知
如果长方形的面积一定,长与宽成反比例关系。
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
区别判断正比例和反比例的方法:
正比例:两个相关联的量,比值一定。
反比例:两个相关联的量,乘积一定。
五
巩固练习
(1)分子一定,分母和分数值成反比例。
(2)2×5=10,所以2和5成反比例。
(3)三角形面积一定,底和高成反比例。
1.判断对错,并说说为什么。
×
( )
√
( )
( )
√
A B
√
×
分母×分数值=分子(一定)
4.煤的数量一定,使用天数与每天的平均用煤量。
A B
√
×
使用天数×每天的平均用煤量=煤的总吨数(一定)
5.全班人数一定,按各组人数相等的要求分组,组数与每组的人数。
组数×每组的人数=总人数(一定)
6.在一块菜地上种的黄瓜与西红柿的面积。
不成反比例,因为种黄瓜的面积+西红柿的面积=总面积
四
课堂小结
两种相关联的量,一种量的变化,另一种量也随着变化,这两种量中相对的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系,用字母表示为:
x y=k
(一定)
2.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
因为:地砖数×每块地砖的面积=教室总面积(一定)
所以:所需地砖数量与每块地砖的面积成反比例关系
900×600=540000(cm )=54(m )
1800×300=540000(cm )=54(m )
3600×150=540000(cm )=54(m )
3.食品加工厂准备把一批新酿的醋装瓶运往商店。
所装瓶数与每瓶容量是否成反比例关系?为什么?
因为:每瓶容量×所装瓶数=醋的体积(一定)。
所以:所装瓶数与每瓶容量成反比例关系。
250×1200=300000(ml)=300(L)
500×600=300000(ml)=300(L)
750×400=300000(ml)=300(L)
6.在一块菜地上种的黄瓜与西红柿的面积。
不成反比例,因为种黄瓜的面积+西红柿的面积=总面积
7.书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
成反比例,因为每包的册数×包数=书的总册数(一定)
六
拓展练习
P52T15
优翼
1.有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成 比例关系。
(2)当x一定时,z与y成 比例关系。
(3)当y一定时,z与x成 比例关系。
反
正
正
0
12. 一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装手机总数之间的关系吗?
(2)p与t成什么比例关系?
(1)答:手机总数=pt
(2)答:p、t成反比例关系。
练习九
0
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
500×24÷8=1500(部)
答:每天组装1500部手机。
练习九
五
巩固练习
4.下表中x和y两个量成反比例关系,请把表格填写完整。
50
100
0.25
12
P51T10
优翼
六
拓展练习
P52T16
优翼
2.一个长方形的面积是36cm2,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
y与x成反比例关系,图象不是一条直线。
0
4. 已知y与x成正比例关系,在下表的空格中填写合适的数。
5
12.5
25
50
3
8
15
练习九
0
13. 京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
(1)京沪高铁全长多少千米?
260×5=1300(千米)
答:京沪高铁全长1300千米。
练习九
0
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
答:t与v成反比例。关系式:tv=1300。
1300÷325=4(小时)
答:驶完全程需要4小时。
练习九
0
13. 京沪高铁的火车平均行驶速度与驶完全程所需时间如下表。
(1)京沪高铁全长多少千米?
260×5=1300(千米)
答:京沪高铁全长1300千米。
练习九
0
14. 右面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑得快还是长颈鹿跑的快?
答:斑马和长颈鹿的奔跑路程和奔跑时间都成正比例关系。
答:从图象中可知斑马18分钟大约跑22km,长颈鹿18分钟大约跑14km。
答:从图象上看,斑马跑的快。
练习九
0
16*. 一个长方形的面积是36cm ,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
答:长方形的面积=长×宽,xy=36,y与x的乘积一定,所以y与x成方比例关系。
列举数据:
x/cm
y/cm
9
12
18
36
4
3
2
1
0
4
8
12
16
20
24
28
32
36
x/cm
4
8
12
16
20
24
28
32
36
y/cm
所以xy=36的图象不是一条直线,而是一条曲线。
练习九
