RJ数学八下专题课堂(八) 平行四边形中的动态问题(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(八) 平行四边形中的动态问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 09:23:14 | ||
图片预览


文档简介
RJ数学八下专题课堂(八) 平行四边形中的动态问题
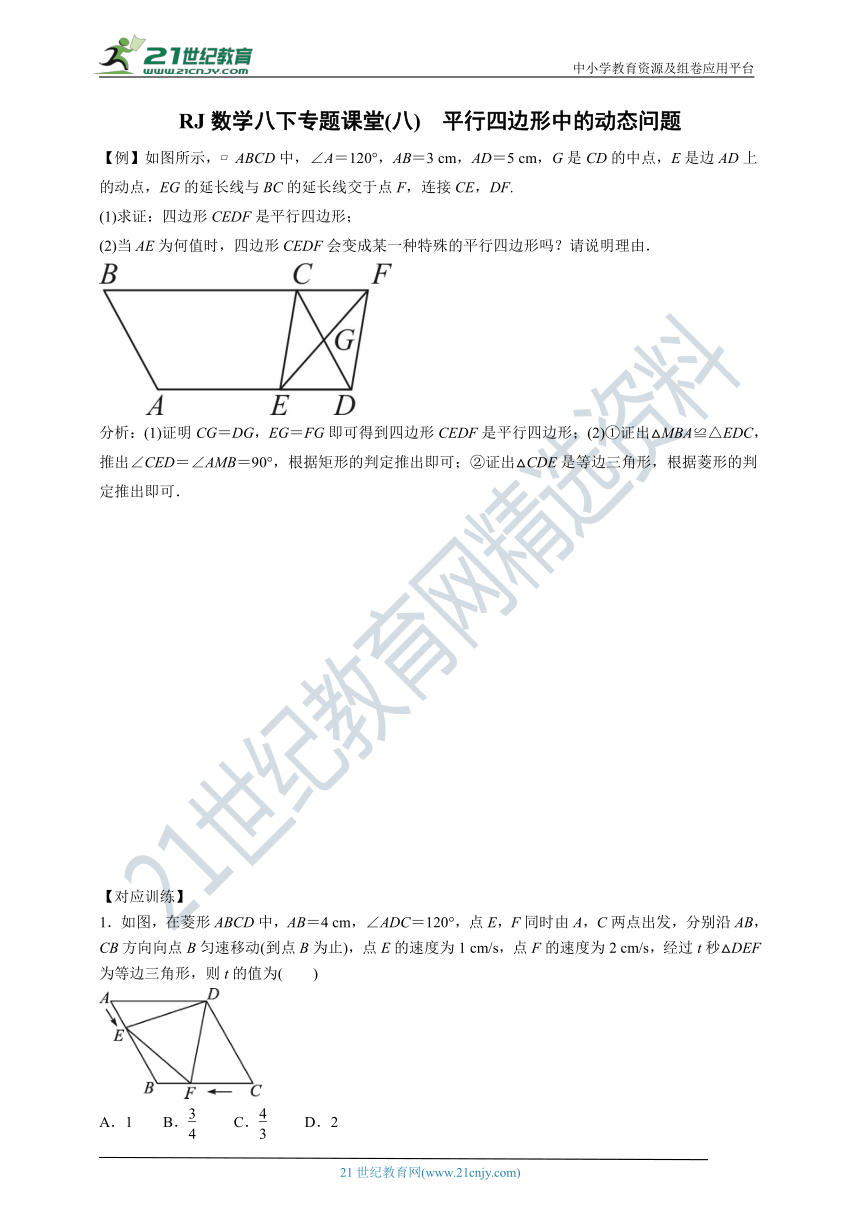
【例】如图所示, ABCD中,∠A=120°,AB=3 cm,AD=5 cm,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)当AE为何值时,四边形CEDF会变成某一种特殊的平行四边形吗?请说明理由.
分析:(1)证明CG=DG,EG=FG即可得到四边形CEDF是平行四边形;(2)①证出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;②证出△CDE是等边三角形,根据菱形的判定推出即可.
【对应训练】
1.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A.1 B. C. D.2
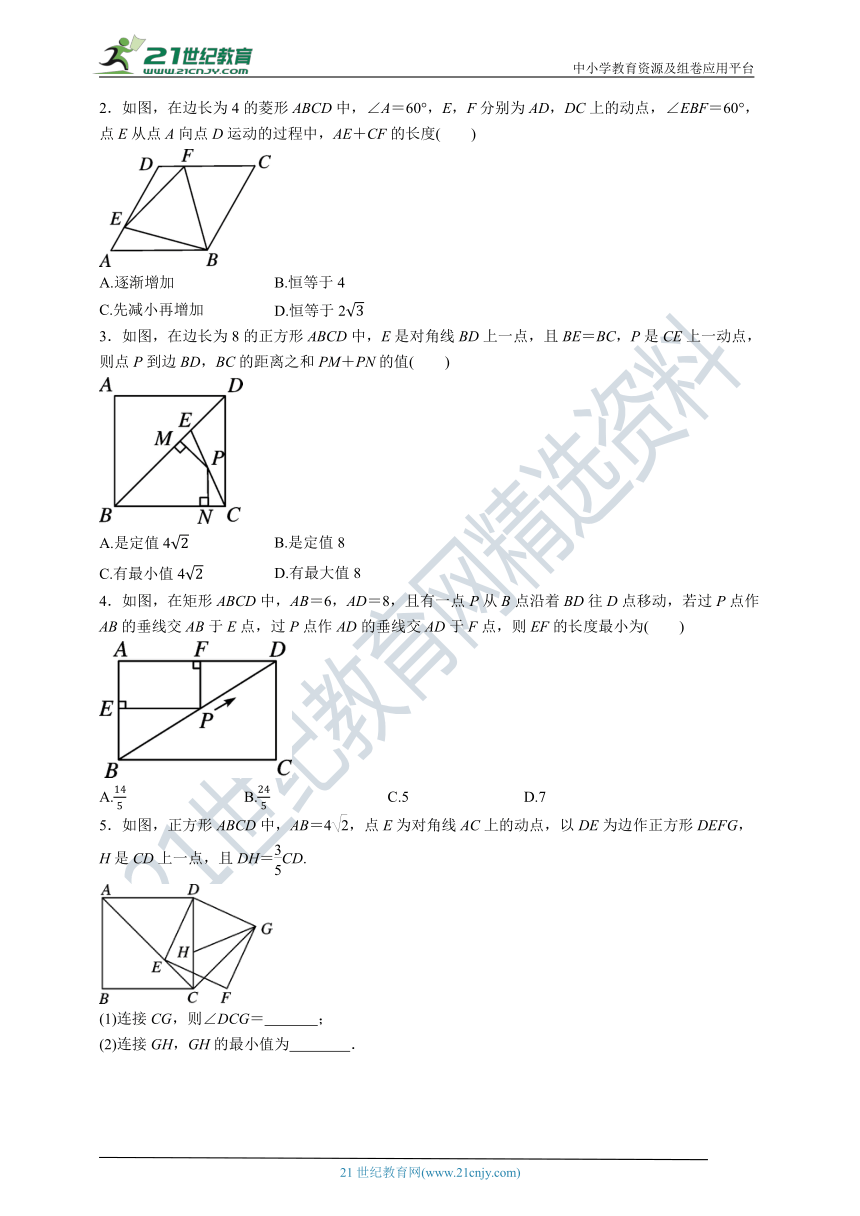
2.如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )
A.逐渐增加 B.恒等于4
C.先减小再增加 D.恒等于2
3.如图,在边长为8的正方形ABCD中,E是对角线BD上一点,且BE=BC,P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值( )
A.是定值4 B.是定值8
C.有最小值4 D.有最大值8
4.如图,在矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为( )
A. B. C.5 D.7
5.如图,正方形ABCD中,AB=4,点E为对角线AC上的动点,以DE为边作正方形DEFG,
H是CD上一点,且DH=CD.
(1)连接CG,则∠DCG= ;
(2)连接GH,GH的最小值为 .
6.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图①,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,AG的长为________.
7.在矩形ABCD中,AB=6,BC=8,G,H分别是AD,BC的中点,E,F是对角线AC上的两个动点,它们分别从A,C两点同时以每秒1个单位长度的速度出发相向而行,运动时间为t秒.
(1)当0<t<5时,判断四边形EGFH的形状,并说明理由;
(2)当0<t<10时,若四边形EGFH为矩形,请直接写出t的值为 .
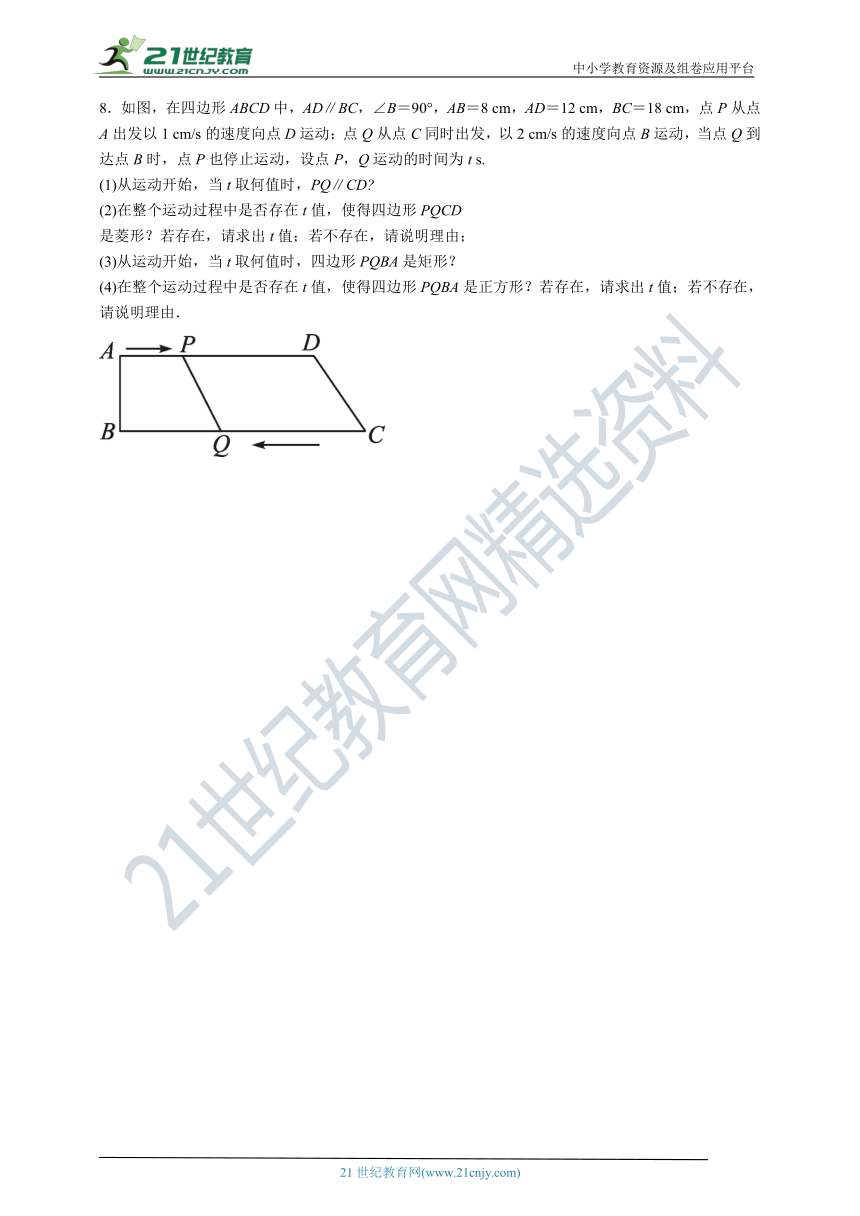
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发以1 cm/s的速度向点D运动;点Q从点C同时出发,以2 cm/s的速度向点B运动,当点Q到达点B时,点P也停止运动,设点P,Q运动的时间为t s.
(1)从运动开始,当t取何值时,PQ∥CD
(2)在整个运动过程中是否存在t值,使得四边形PQCD
是菱形?若存在,请求出t值;若不存在,请说明理由;
(3)从运动开始,当t取何值时,四边形PQBA是矩形?
(4)在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【例】如图所示, ABCD中,∠A=120°,AB=3 cm,AD=5 cm,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)当AE为何值时,四边形CEDF会变成某一种特殊的平行四边形吗?请说明理由.
分析:(1)证明CG=DG,EG=FG即可得到四边形CEDF是平行四边形;(2)①证出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;②证出△CDE是等边三角形,根据菱形的判定推出即可.
解:(1)∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,在△FCG和△EDG中, ∴△FCG≌△EDG (ASA),∴FG=EG,∵CG=DG,∴四边形CEDF是平行四边形
(2)①当AE=3.5时,平行四边形CEDF是矩形,理由是:过A作AM⊥BC于M,∵∠B=60°,AB=3,∴BM=1.5,∵四边形ABCD是平行四边形,∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,∵AE=3.5,∴DE=1.5=BM,在△MBA和△EDC中,∴△MBA≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF是平行四边形,∴四边形CEDF是矩形.
②当AE=2时,四边形CEDF是菱形,理由是:∵AD=5,AE=2,∴DE=3,∵CD=3,∠CDE=60°,∴△CDE是等边三角形,∴CE=DE,∵四边形CEDF是平行四边形,∴四边形CEDF是菱形
【对应训练】
1.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为( C )
A.1 B. C. D.2
【解析】连接BD,证出△ADE≌△BDF,得到AE=BF,再利用AE=t,CF=2t,则BF=BC-CF=4-2t求出时间t的值.
2.如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( B )
A.逐渐增加 B.恒等于4
C.先减小再增加 D.恒等于2
3.如图,在边长为8的正方形ABCD中,E是对角线BD上一点,且BE=BC,P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值( A )
A.是定值4 B.是定值8
C.有最小值4 D.有最大值8
4.如图,在矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为( B )
A. B. C.5 D.7
5.如图,正方形ABCD中,AB=4 ,点E为对角线AC上的动点,以DE为边作正方形DEFG,
H是CD上一点,且DH=CD.
(1)连接CG,则∠DCG= ;
(2)连接GH,GH的最小值为 .
【答案】45°
6.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图①,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,AG的长为________.
解:(1)①∵四边形ABCD是菱形,∴AB=BC,∴∠BAC=∠BCA,∵四边形EFGH是矩形,∴FG∥BC,∴∠FGA=∠BCA,∴∠BCA=∠BAC,∴AF=FG ②连接BG,∵AB=BC,点G是AC的中点,∴BG⊥AC,∴∠BGA=90°,即∠BGF+∠FGA=90°,在Rt△ABG中,∠FAG+∠ABG=90°,∵∠FAG=∠FGA,∴∠FBG=∠FGB,∴BF=FG
(2)7
7.在矩形ABCD中,AB=6,BC=8,G,H分别是AD,BC的中点,E,F是对角线AC上的两个动点,它们分别从A,C两点同时以每秒1个单位长度的速度出发相向而行,运动时间为t秒.
(1)当0<t<5时,判断四边形EGFH的形状,并说明理由;
(2)当0<t<10时,若四边形EGFH为矩形,请直接写出t的值为 .
解:(1)四边形EGFH是平行四边形.理由如下:
由题意,得AE=CF=t,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.∴∠GAE=∠HCF.
∵G,H分别是AD,BC的中点,
∴AG=AD,CH=BC.∴AG=CH.
在△AEG和△CFH中,
∴△AEG≌△CFH(SAS).
∴EG=FH,∠AEG=∠CFH.
∴∠FEG=∠EFH.∴EG∥HF.
∴四边形EGFH是平行四边形.
(2)2或8
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发以1 cm/s的速度向点D运动;点Q从点C同时出发,以2 cm/s的速度向点B运动,当点Q到达点B时,点P也停止运动,设点P,Q运动的时间为t s.
(1)从运动开始,当t取何值时,PQ∥CD
(2)在整个运动过程中是否存在t值,使得四边形PQCD
是菱形?若存在,请求出t值;若不存在,请说明理由;
(3)从运动开始,当t取何值时,四边形PQBA是矩形?
(4)在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
解:(1)由题意知,AP=t cm,CQ=2t cm,∴DP=AD-AP=(12-t)cm,∵AD∥BC,若要PQ∥CD,则四边形PQCD为平行四边形,∴DP=CQ,∴12-t=2t,∴t=4,即t=4时,PQ∥CD
(2)不存在,理由:∵四边形PQCD是菱形,∴CQ=CD,∴2t=10,∴t=5,此时,DP=AD-AP=12-5=7(cm),而DP≠CD,∴四边形PQCD不可能是菱形
(3)∵∠B=90°,AD∥BC,∴当AP=BQ时,四边形PQBA是矩形,即t=18-2t,解得t=6,∴当t=6时,四边形PQBA是矩形
(4)不存在.理由:由当t=6时,四边形PQBA是矩形,可得AP=6 cm,∵AB=8 cm,∴AP≠AB,∴矩形PQBA不能是正方形,即不存在时间t,使四边形PQBA是正方形
【例】如图所示, ABCD中,∠A=120°,AB=3 cm,AD=5 cm,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)当AE为何值时,四边形CEDF会变成某一种特殊的平行四边形吗?请说明理由.
分析:(1)证明CG=DG,EG=FG即可得到四边形CEDF是平行四边形;(2)①证出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;②证出△CDE是等边三角形,根据菱形的判定推出即可.
【对应训练】
1.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A.1 B. C. D.2
2.如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )
A.逐渐增加 B.恒等于4
C.先减小再增加 D.恒等于2
3.如图,在边长为8的正方形ABCD中,E是对角线BD上一点,且BE=BC,P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值( )
A.是定值4 B.是定值8
C.有最小值4 D.有最大值8
4.如图,在矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为( )
A. B. C.5 D.7
5.如图,正方形ABCD中,AB=4,点E为对角线AC上的动点,以DE为边作正方形DEFG,
H是CD上一点,且DH=CD.
(1)连接CG,则∠DCG= ;
(2)连接GH,GH的最小值为 .
6.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图①,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,AG的长为________.
7.在矩形ABCD中,AB=6,BC=8,G,H分别是AD,BC的中点,E,F是对角线AC上的两个动点,它们分别从A,C两点同时以每秒1个单位长度的速度出发相向而行,运动时间为t秒.
(1)当0<t<5时,判断四边形EGFH的形状,并说明理由;
(2)当0<t<10时,若四边形EGFH为矩形,请直接写出t的值为 .
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发以1 cm/s的速度向点D运动;点Q从点C同时出发,以2 cm/s的速度向点B运动,当点Q到达点B时,点P也停止运动,设点P,Q运动的时间为t s.
(1)从运动开始,当t取何值时,PQ∥CD
(2)在整个运动过程中是否存在t值,使得四边形PQCD
是菱形?若存在,请求出t值;若不存在,请说明理由;
(3)从运动开始,当t取何值时,四边形PQBA是矩形?
(4)在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【例】如图所示, ABCD中,∠A=120°,AB=3 cm,AD=5 cm,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)当AE为何值时,四边形CEDF会变成某一种特殊的平行四边形吗?请说明理由.
分析:(1)证明CG=DG,EG=FG即可得到四边形CEDF是平行四边形;(2)①证出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;②证出△CDE是等边三角形,根据菱形的判定推出即可.
解:(1)∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,在△FCG和△EDG中, ∴△FCG≌△EDG (ASA),∴FG=EG,∵CG=DG,∴四边形CEDF是平行四边形
(2)①当AE=3.5时,平行四边形CEDF是矩形,理由是:过A作AM⊥BC于M,∵∠B=60°,AB=3,∴BM=1.5,∵四边形ABCD是平行四边形,∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,∵AE=3.5,∴DE=1.5=BM,在△MBA和△EDC中,∴△MBA≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF是平行四边形,∴四边形CEDF是矩形.
②当AE=2时,四边形CEDF是菱形,理由是:∵AD=5,AE=2,∴DE=3,∵CD=3,∠CDE=60°,∴△CDE是等边三角形,∴CE=DE,∵四边形CEDF是平行四边形,∴四边形CEDF是菱形
【对应训练】
1.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为( C )
A.1 B. C. D.2
【解析】连接BD,证出△ADE≌△BDF,得到AE=BF,再利用AE=t,CF=2t,则BF=BC-CF=4-2t求出时间t的值.
2.如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( B )
A.逐渐增加 B.恒等于4
C.先减小再增加 D.恒等于2
3.如图,在边长为8的正方形ABCD中,E是对角线BD上一点,且BE=BC,P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值( A )
A.是定值4 B.是定值8
C.有最小值4 D.有最大值8
4.如图,在矩形ABCD中,AB=6,AD=8,且有一点P从B点沿着BD往D点移动,若过P点作AB的垂线交AB于E点,过P点作AD的垂线交AD于F点,则EF的长度最小为( B )
A. B. C.5 D.7
5.如图,正方形ABCD中,AB=4 ,点E为对角线AC上的动点,以DE为边作正方形DEFG,
H是CD上一点,且DH=CD.
(1)连接CG,则∠DCG= ;
(2)连接GH,GH的最小值为 .
【答案】45°
6.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图①,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,AG的长为________.
解:(1)①∵四边形ABCD是菱形,∴AB=BC,∴∠BAC=∠BCA,∵四边形EFGH是矩形,∴FG∥BC,∴∠FGA=∠BCA,∴∠BCA=∠BAC,∴AF=FG ②连接BG,∵AB=BC,点G是AC的中点,∴BG⊥AC,∴∠BGA=90°,即∠BGF+∠FGA=90°,在Rt△ABG中,∠FAG+∠ABG=90°,∵∠FAG=∠FGA,∴∠FBG=∠FGB,∴BF=FG
(2)7
7.在矩形ABCD中,AB=6,BC=8,G,H分别是AD,BC的中点,E,F是对角线AC上的两个动点,它们分别从A,C两点同时以每秒1个单位长度的速度出发相向而行,运动时间为t秒.
(1)当0<t<5时,判断四边形EGFH的形状,并说明理由;
(2)当0<t<10时,若四边形EGFH为矩形,请直接写出t的值为 .
解:(1)四边形EGFH是平行四边形.理由如下:
由题意,得AE=CF=t,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.∴∠GAE=∠HCF.
∵G,H分别是AD,BC的中点,
∴AG=AD,CH=BC.∴AG=CH.
在△AEG和△CFH中,
∴△AEG≌△CFH(SAS).
∴EG=FH,∠AEG=∠CFH.
∴∠FEG=∠EFH.∴EG∥HF.
∴四边形EGFH是平行四边形.
(2)2或8
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发以1 cm/s的速度向点D运动;点Q从点C同时出发,以2 cm/s的速度向点B运动,当点Q到达点B时,点P也停止运动,设点P,Q运动的时间为t s.
(1)从运动开始,当t取何值时,PQ∥CD
(2)在整个运动过程中是否存在t值,使得四边形PQCD
是菱形?若存在,请求出t值;若不存在,请说明理由;
(3)从运动开始,当t取何值时,四边形PQBA是矩形?
(4)在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
解:(1)由题意知,AP=t cm,CQ=2t cm,∴DP=AD-AP=(12-t)cm,∵AD∥BC,若要PQ∥CD,则四边形PQCD为平行四边形,∴DP=CQ,∴12-t=2t,∴t=4,即t=4时,PQ∥CD
(2)不存在,理由:∵四边形PQCD是菱形,∴CQ=CD,∴2t=10,∴t=5,此时,DP=AD-AP=12-5=7(cm),而DP≠CD,∴四边形PQCD不可能是菱形
(3)∵∠B=90°,AD∥BC,∴当AP=BQ时,四边形PQBA是矩形,即t=18-2t,解得t=6,∴当t=6时,四边形PQBA是矩形
(4)不存在.理由:由当t=6时,四边形PQBA是矩形,可得AP=6 cm,∵AB=8 cm,∴AP≠AB,∴矩形PQBA不能是正方形,即不存在时间t,使四边形PQBA是正方形
