RJ数学八下专题课堂(九) 平行四边形中的折叠问题(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(九) 平行四边形中的折叠问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 00:00:00 | ||
图片预览



文档简介
RJ数学八下专题课堂(九) 平行四边形中的折叠问题
一、平行四边形的折叠
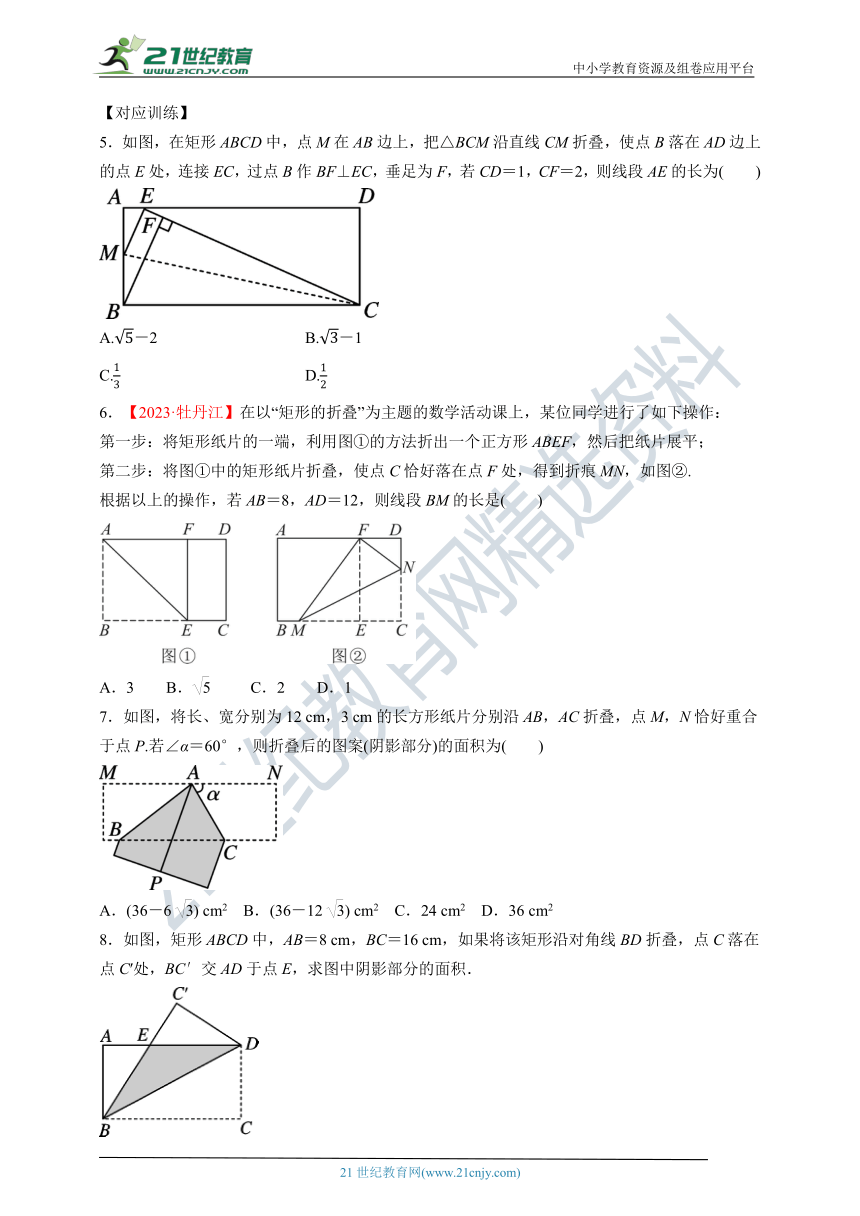
【例1】如图,将 ABCD沿对角线BD折叠,点A落在点E处,∠1=56°,∠ABC=70°,求∠2的度数.
分析:先由平行四边形的性质和折叠的性质求得∠ABD=∠CDB=∠EBD,然后由三角形的外角性质求得 ∠ABD=∠CDB=28°,由平行四边形对边平行求得 ∠A=110°,最后由三角形内角和定理即可求出 ∠2的度数.
【对应训练】
1.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E的度数为( )
A.102° B.112°
C.122° D.92°
2.【2023·宜昌】如图,小宇将一张平行四边形纸片折叠,使点A落在长边CD上的点A'处,并得到折痕DE,小宇测得长边CD=8,则四边形A'EBC的周长为 .
3.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F.若∠B=80°,∠ACE=2∠ECD.FC=a,FD=b,则 ABCD的周长为 .
4.如图,在平行四边形ABCD中,已知AD=,∠DAB=45°,AB=3,如果把该平行四边形折叠,点A恰好与点C重合,求折痕EF的长.
二、矩形的折叠
【例2】如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O,若AE=5,BF=3,求AC的长.
分析:先由平行四边形的性质和折叠的性质求得AE=AF=5,再由折叠得FC=AF,最后由勾股定理即可求出 AC的长.
【对应训练】
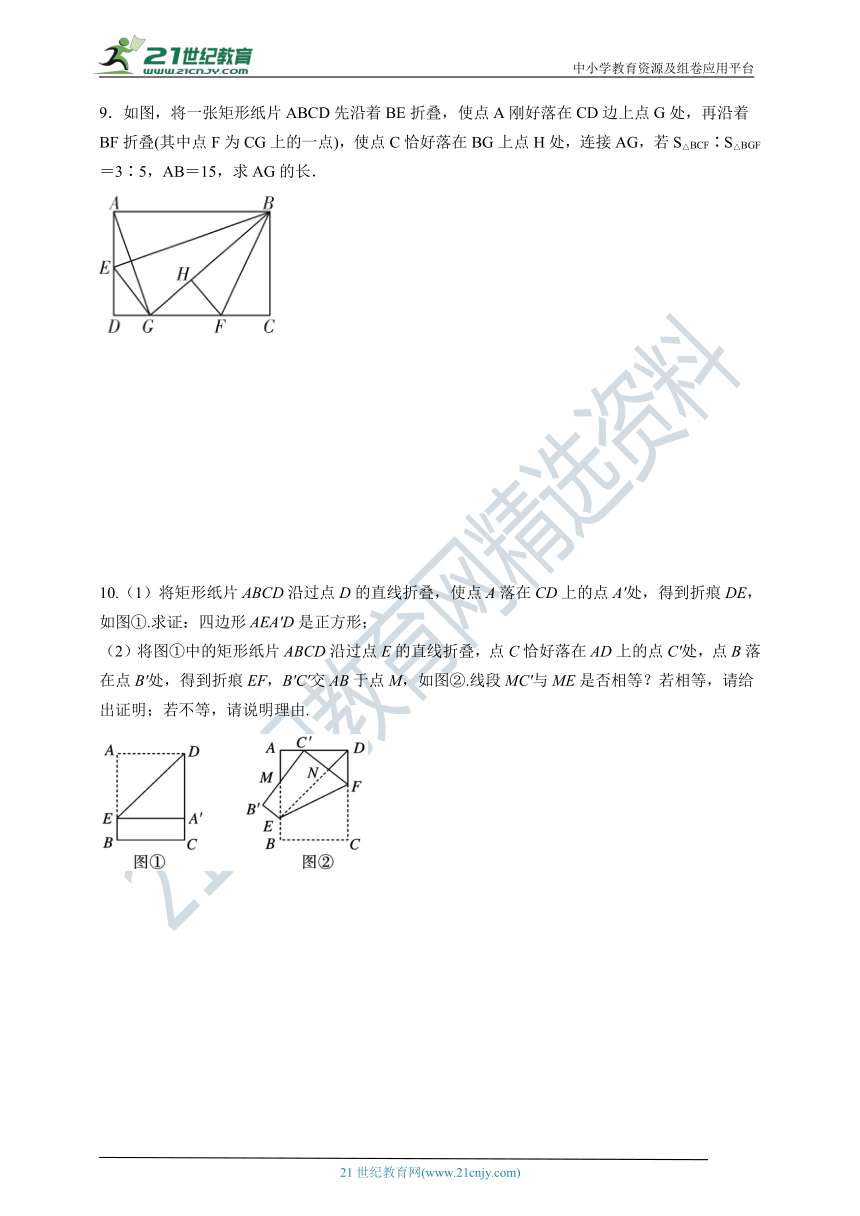
5.如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为( )
A.-2 B.-1
C. D.
6.【2023·牡丹江】在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( )
A.3 B. C.2 D.1
7.如图,将长、宽分别为12 cm,3 cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)的面积为( )
A.(36-6 ) cm2 B.(36-12 ) cm2 C.24 cm2 D.36 cm2
8.如图,矩形ABCD中,AB=8 cm,BC=16 cm,如果将该矩形沿对角线BD折叠,点C落在点C′处,BC′交AD于点E,求图中阴影部分的面积.
9.如图,将一张矩形纸片ABCD先沿着BE折叠,使点A刚好落在CD边上点G处,再沿着BF折叠(其中点F为CG上的一点),使点C恰好落在BG上点H处,连接AG,若S△BCF∶S△BGF=3∶5,AB=15,求AG的长.
10.(1)将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,如图①.求证:四边形AEA'D是正方形;
(2)将图①中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,如图②.线段MC'与ME是否相等?若相等,请给出证明;若不等,请说明理由.
三、菱形的折叠
【例3】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G(不与B,D重合),折痕为EF,若DG=2,BG=6,求BE的长.
分析:由菱形的性质易知△ABD为等边三角形,从而得到AB=BD=8,由折叠的性质可知,EG=EA,作EH⊥BD于H,设BE=x,根据勾股定理列方程求出x即可.
【对应训练】
11.如图,将菱形ABCD的边AD以直线AN为对称轴翻折至AM,使点C恰好落在AM上.若此时CM=CN,则∠D的度数为( )
A.30° B.54° C.45° D.36°
12.如图,已知四边形ABCD是边长为6的菱形,且∠BAD=120°,点E,F分别在AB,BC边上,将菱形沿EF折叠,点B正好落在AD边的点G处,若EG⊥AC,则FG的长为( )
A.3 B.6 C.3 D.3
13.如图,菱形ABCD的边长为4,∠A=60°,将菱形沿EF折叠,顶点C恰好落在AB边的中点G处,求BF的长.
14.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长为2,∠A=120°,求EF的长.
四、正方形的折叠
【例4】如图,四边形ABCD为正方形,点E是BC的中点,将正方形ABCD沿AE折叠,得到点B的对应点为点F,延长EF交线段DC于点P,若AB=6,求DP的长.
分析:由正方形的性质和折叠的性质可证明Rt△AFP≌Rt△ADP,所以PF=PD,设PF=PD=x,由勾股定理列方程求出x即可.
【对应训练】
15.如图,正方形ABCD的边长为4,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=3∶1,则线段CH的长是( )
A.3 B. C.1 D.2
16.如图,正方形纸片ABCD的边长为4,E,F,H分别是边BC,CD,AB上的一点,将纸片沿FH折叠,使点D恰好落在BC边的中点E处,点A的对应点为P,则折痕FH的长为 .
17.如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
18.如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,求BF2的值.
19.如图,正方形ABCD中,点E在边CD上,且CD=3DE.将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,连接AG,CF.
(1)求∠EAG的度数;
(2)求证:AG∥CF;
(3)若AB=6,则△GCF的面积等于 .
20.如图,将一块边长为9的正方形纸片ABCD的顶点A折叠至DC边上的点E处,使DE=3,折痕为PQ,连接AE交PQ于点M.
求:(1)PA的长;
(2)PM的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、平行四边形的折叠
【例1】如图,将 ABCD沿对角线BD折叠,点A落在点E处,∠1=56°,∠ABC=70°,求∠2的度数.
分析:先由平行四边形的性质和折叠的性质求得∠ABD=∠CDB=∠EBD,然后由三角形的外角性质求得 ∠ABD=∠CDB=28°,由平行四边形对边平行求得 ∠A=110°,最后由三角形内角和定理即可求出 ∠2的度数.
解:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ABD=∠CDB,由折叠的性质得:∠EBD=∠ABD,∴∠ABD=∠CDB=∠EBD,∵∠1=∠CDB+∠EBD=56°,∴∠ABD=∠CDB=28°,∵AD∥BC,∠ABC=70°,∴∠A=180°-∠ABC=180°-70°=110°,∴∠2=180°-∠ABD-∠A=180°-28°-110°=42°
【对应训练】
1.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E的度数为( B )
A.102° B.112°
C.122° D.92°
2.【2023·宜昌】如图,小宇将一张平行四边形纸片折叠,使点A落在长边CD上的点A'处,并得到折痕DE,小宇测得长边CD=8,则四边形A'EBC的周长为 .
【答案】16
3.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F.若∠B=80°,∠ACE=2∠ECD.FC=a,FD=b,则 ABCD的周长为 .
【答案】4a+2b
4.如图,在平行四边形ABCD中,已知AD=,∠DAB=45°,AB=3,如果把该平行四边形折叠,点A恰好与点C重合,求折痕EF的长.
解:如图,过A点作CD的垂线,与CD的延长线交于G点,连接AE,CF,∵AD=,∠DAB=45°,∴△ADG为等腰直角三角形,AG=GD=1,
设AE=x,由折叠可知,EC=AE=x,DE=3-x,在Rt△AGE中,由勾股定理得:AG2+GE2=AE2,即12+(1+3-x)2=x2,解得x=;在Rt△AGC中,由勾股定理得:AC===,∵EF⊥AC,根据菱形AECF计算面积的方法可知,AG·EC=EF·AC,即1×=EF×,解得EF=
二、矩形的折叠
【例2】如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O,若AE=5,BF=3,求AC的长.
分析:先由平行四边形的性质和折叠的性质求得AE=AF=5,再由折叠得FC=AF,最后由勾股定理即可求出 AC的长.
解:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,AB=CD,∴∠EFC=∠AEF,由折叠,得∠EFC=∠AFE,∴∠AFE=∠AEF,∴AE=AF=5,由折叠得,FC=AF,OA=OC,∴BC=3+5=8,在Rt△ABF中,AB==4,在Rt△ABC中,AC==4
【对应训练】
5.如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为( A )
A.-2 B.-1
C. D.
6.【2023·牡丹江】在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( C )
A.3 B. C.2 D.1
7.如图,将长、宽分别为12 cm,3 cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)的面积为( A )
A.(36-6 ) cm2 B.(36-12 ) cm2 C.24 cm2 D.36 cm2
8.如图,矩形ABCD中,AB=8 cm,BC=16 cm,如果将该矩形沿对角线BD折叠,点C落在点C′处,BC′交AD于点E,求图中阴影部分的面积.
解:∵四边形ABCD是矩形,
∴AB=CD=8 cm,BC=AD=16 cm,
AD∥BC,∠A=90°,
∴∠EDB=∠CBD.
由折叠可知,∠EBD=∠CBD,
∴∠EBD=∠EDB,∴BE=DE.
设DE为x cm,则AE=(16-x) cm,BE=x cm,
由勾股定理,得AB2+AE2=BE2.
∴64+(16-x)2=x2,解得x=10.
∴DE=10 cm,
∴阴影部分的面积为×DE×AB=40(cm2).
9.如图,将一张矩形纸片ABCD先沿着BE折叠,使点A刚好落在CD边上点G处,再沿着BF折叠(其中点F为CG上的一点),使点C恰好落在BG上点H处,连接AG,若S△BCF∶S△BGF=3∶5,AB=15,求AG的长.
解:∵四边形ABCD是矩形,∴∠D=∠C=90°,DC=AB=15,
∴FC⊥BC.由折叠得GB=AB=15,FC=FH,
∠C=∠BHF=90°,∴FH⊥GB.
∵S△BCF∶S△BGF=3∶5,∴∶=3∶5,
∴BC∶GB=3∶5,∴BC=GB=×15=9,∴AD=BC=9,
∴CG===12,∴DG=DC-CG=15-12=3,
∴AG===3.
10.(1)将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,如图①.求证:四边形AEA'D是正方形;
(2)将图①中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,如图②.线段MC'与ME是否相等?若相等,请给出证明;若不等,请说明理由.
解:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°.
∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,
∴AD=A'D,AE=A'E,∠ADE=∠A'DE=45°.
∵AB∥CD,∴∠AED=∠A'DE=∠ADE.
∴AD=AE.∴AD=AE=A'E=A’D.
∴四边形AEA'D是菱形.
∵∠A=90°,∴四边形AEA'D是正方形.
(2)MC'=ME.
证明:如图②,连接C'E,由(1)知,AD=AE,
∵四边形ABCD是矩形,
∴AD=BC,∠EAC'=∠B=90°.
由折叠知,B'C'=BC,∠B=∠B',
∴AE=B'C',∠EAC'=∠B'.
在Rt△EC'A和Rt△C'EB'中,
∴Rt△EC'A≌Rt△C'EB'(HL).
∴∠C'EA=∠EC'B'.∴MC'=ME.
三、菱形的折叠
【例3】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G(不与B,D重合),折痕为EF,若DG=2,BG=6,求BE的长.
分析:由菱形的性质易知△ABD为等边三角形,从而得到AB=BD=8,由折叠的性质可知,EG=EA,作EH⊥BD于H,设BE=x,根据勾股定理列方程求出x即可.
解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意,得BD=DG+BG=8. ∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8-x,在Rt△EHB中,∵∠ABD=60°,∠BHE=90°,∴BH=x,EH===x,在Rt△EHG中,EG2=EH2+GH2,即(8-x)2=(x)2+(6-x)2,解得x=2.8,即BE=2.8
【对应训练】
11.如图,将菱形ABCD的边AD以直线AN为对称轴翻折至AM,使点C恰好落在AM上.若此时CM=CN,则∠D的度数为( D )
A.30° B.54° C.45° D.36°
12.如图,已知四边形ABCD是边长为6的菱形,且∠BAD=120°,点E,F分别在AB,BC边上,将菱形沿EF折叠,点B正好落在AD边的点G处,若EG⊥AC,则FG的长为( C )
A.3 B.6 C.3 D.3
13.如图,菱形ABCD的边长为4,∠A=60°,将菱形沿EF折叠,顶点C恰好落在AB边的中点G处,求BF的长.
解:过F作FH⊥AB,交AB的延长线于点H,∵∠A=60°,AD∥BC,∴∠HBF=60°,∠BFH=30°,设BH=x,则BF=2x,CF=4-2x=GF,FH=x,∵G是AB的中点,∴BG=2,GH=2+x,Rt△FGH中,FH2+GH2=GF2,∴(x)2+(2+x)2=(4-2x)2,解得x=0.6,∴BF=2x=1.2
14.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长为2,∠A=120°,求EF的长.
解:如图,连接BD,AC,则O为AC与BD的交点.
∵四边形ABCD是菱形,
∴AC⊥BD,AC平分∠BAD.
∵∠BAD=120°,∴∠BAC=60°.
∴∠ABO=90°-60°=30°.
∴AO=AB=×2=1.
设OA与EF的交点为G,由折叠知,
AG=AO=,OA⊥EF,
∴由勾股定理,得EG=,
∴EF=2EG=.
四、正方形的折叠
【例4】如图,四边形ABCD为正方形,点E是BC的中点,将正方形ABCD沿AE折叠,得到点B的对应点为点F,延长EF交线段DC于点P,若AB=6,求DP的长.
分析:由正方形的性质和折叠的性质可证明Rt△AFP≌Rt△ADP,所以PF=PD,设PF=PD=x,由勾股定理列方程求出x即可.
解:连接AP,∵四边形ABCD为正方形,∴AB=BC=AD=6,∠B=∠C=∠D=90°,点E是BC的中点,∴BE=CE=3,由翻折可知:AF=AB,EF=BE=3,∠AFE=∠B=90°,∴AD=AF,∠AFP=∠D=90°,在Rt△AFP和Rt△ADP中, ∴Rt△AFP≌Rt△ADP(HL),∴PF=PD,设PF=PD=x,则CP=CD-PD=6-x,EP=EF+FP=3+x,在Rt△PEC中,根据勾股定理得:EP2=EC2+CP2,∴(3+x)2=32+(6-x)2,解得x=2.即DP的长度为2
【对应训练】
15.如图,正方形ABCD的边长为4,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=3∶1,则线段CH的长是( B )
A.3 B. C.1 D.2
16.如图,正方形纸片ABCD的边长为4,E,F,H分别是边BC,CD,AB上的一点,将纸片沿FH折叠,使点D恰好落在BC边的中点E处,点A的对应点为P,则折痕FH的长为 .
【答案】2
17.如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
【答案】
18.如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,求BF2的值.
解:过点F作FG⊥BC交于G点,
由折叠可知DE=EF,AD=AF,∠D=∠EFA=90°,
设正方形的边长为x,∵EF=2,
∴DE=2,EC=x-2,AC=x,
在Rt△EFC中,EC2=FE2+FC2,∴(x-2)2=4+(x-x)2,
解得x=2+2,∴FC=x-x=2,
∵∠ACB=45°,∴由勾股定理得FG=CG=,
∴BG=+2,在Rt△BFG中,
BF2=BG2+GF2=(+2)2+2=8+4.
19.如图,正方形ABCD中,点E在边CD上,且CD=3DE.将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,连接AG,CF.
(1)求∠EAG的度数;
(2)求证:AG∥CF;
(3)若AB=6,则△GCF的面积等于 .
(1)解:∠EAG=45°.
(2)证明:设BG=FG=x,DE=EF=a,则BC=CD=3a,CE=2a.
在Rt△ECG中,由勾股定理,得CG2+CE2=EG2,
即(3a-x)2+(2a)2=(x+a)2,解得x=a.
∴FG=BG=GC,∴∠GCF=∠GFC,
∵∠BGF=∠GCF+∠GFC=2∠GCF,∠BGF=2∠BGA,
∴∠GCF=∠BGA,∴AG∥CF.
(3)
20.如图,将一块边长为9的正方形纸片ABCD的顶点A折叠至DC边上的点E处,使DE=3,折痕为PQ,连接AE交PQ于点M.
求:(1)PA的长;
(2)PM的长.
解:(1)如图所示,连接PE,由折叠可得,PQ垂直平分AE,
∴PA=PE,
设AP=PE=x,则PD=9-x,Rt△DEP中,DE2+DP2=PE2,即32+(9-x)2=x2,
解得x=5,∴AP=5.
(2)Rt△ADE中,AE===3,
∴AM=AE= ,
由折叠可得PQ⊥AE,
∴Rt△APM中,
PM===.
一、平行四边形的折叠
【例1】如图,将 ABCD沿对角线BD折叠,点A落在点E处,∠1=56°,∠ABC=70°,求∠2的度数.
分析:先由平行四边形的性质和折叠的性质求得∠ABD=∠CDB=∠EBD,然后由三角形的外角性质求得 ∠ABD=∠CDB=28°,由平行四边形对边平行求得 ∠A=110°,最后由三角形内角和定理即可求出 ∠2的度数.
【对应训练】
1.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E的度数为( )
A.102° B.112°
C.122° D.92°
2.【2023·宜昌】如图,小宇将一张平行四边形纸片折叠,使点A落在长边CD上的点A'处,并得到折痕DE,小宇测得长边CD=8,则四边形A'EBC的周长为 .
3.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F.若∠B=80°,∠ACE=2∠ECD.FC=a,FD=b,则 ABCD的周长为 .
4.如图,在平行四边形ABCD中,已知AD=,∠DAB=45°,AB=3,如果把该平行四边形折叠,点A恰好与点C重合,求折痕EF的长.
二、矩形的折叠
【例2】如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O,若AE=5,BF=3,求AC的长.
分析:先由平行四边形的性质和折叠的性质求得AE=AF=5,再由折叠得FC=AF,最后由勾股定理即可求出 AC的长.
【对应训练】
5.如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为( )
A.-2 B.-1
C. D.
6.【2023·牡丹江】在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( )
A.3 B. C.2 D.1
7.如图,将长、宽分别为12 cm,3 cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)的面积为( )
A.(36-6 ) cm2 B.(36-12 ) cm2 C.24 cm2 D.36 cm2
8.如图,矩形ABCD中,AB=8 cm,BC=16 cm,如果将该矩形沿对角线BD折叠,点C落在点C′处,BC′交AD于点E,求图中阴影部分的面积.
9.如图,将一张矩形纸片ABCD先沿着BE折叠,使点A刚好落在CD边上点G处,再沿着BF折叠(其中点F为CG上的一点),使点C恰好落在BG上点H处,连接AG,若S△BCF∶S△BGF=3∶5,AB=15,求AG的长.
10.(1)将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,如图①.求证:四边形AEA'D是正方形;
(2)将图①中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,如图②.线段MC'与ME是否相等?若相等,请给出证明;若不等,请说明理由.
三、菱形的折叠
【例3】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G(不与B,D重合),折痕为EF,若DG=2,BG=6,求BE的长.
分析:由菱形的性质易知△ABD为等边三角形,从而得到AB=BD=8,由折叠的性质可知,EG=EA,作EH⊥BD于H,设BE=x,根据勾股定理列方程求出x即可.
【对应训练】
11.如图,将菱形ABCD的边AD以直线AN为对称轴翻折至AM,使点C恰好落在AM上.若此时CM=CN,则∠D的度数为( )
A.30° B.54° C.45° D.36°
12.如图,已知四边形ABCD是边长为6的菱形,且∠BAD=120°,点E,F分别在AB,BC边上,将菱形沿EF折叠,点B正好落在AD边的点G处,若EG⊥AC,则FG的长为( )
A.3 B.6 C.3 D.3
13.如图,菱形ABCD的边长为4,∠A=60°,将菱形沿EF折叠,顶点C恰好落在AB边的中点G处,求BF的长.
14.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长为2,∠A=120°,求EF的长.
四、正方形的折叠
【例4】如图,四边形ABCD为正方形,点E是BC的中点,将正方形ABCD沿AE折叠,得到点B的对应点为点F,延长EF交线段DC于点P,若AB=6,求DP的长.
分析:由正方形的性质和折叠的性质可证明Rt△AFP≌Rt△ADP,所以PF=PD,设PF=PD=x,由勾股定理列方程求出x即可.
【对应训练】
15.如图,正方形ABCD的边长为4,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=3∶1,则线段CH的长是( )
A.3 B. C.1 D.2
16.如图,正方形纸片ABCD的边长为4,E,F,H分别是边BC,CD,AB上的一点,将纸片沿FH折叠,使点D恰好落在BC边的中点E处,点A的对应点为P,则折痕FH的长为 .
17.如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
18.如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,求BF2的值.
19.如图,正方形ABCD中,点E在边CD上,且CD=3DE.将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,连接AG,CF.
(1)求∠EAG的度数;
(2)求证:AG∥CF;
(3)若AB=6,则△GCF的面积等于 .
20.如图,将一块边长为9的正方形纸片ABCD的顶点A折叠至DC边上的点E处,使DE=3,折痕为PQ,连接AE交PQ于点M.
求:(1)PA的长;
(2)PM的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、平行四边形的折叠
【例1】如图,将 ABCD沿对角线BD折叠,点A落在点E处,∠1=56°,∠ABC=70°,求∠2的度数.
分析:先由平行四边形的性质和折叠的性质求得∠ABD=∠CDB=∠EBD,然后由三角形的外角性质求得 ∠ABD=∠CDB=28°,由平行四边形对边平行求得 ∠A=110°,最后由三角形内角和定理即可求出 ∠2的度数.
解:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ABD=∠CDB,由折叠的性质得:∠EBD=∠ABD,∴∠ABD=∠CDB=∠EBD,∵∠1=∠CDB+∠EBD=56°,∴∠ABD=∠CDB=28°,∵AD∥BC,∠ABC=70°,∴∠A=180°-∠ABC=180°-70°=110°,∴∠2=180°-∠ABD-∠A=180°-28°-110°=42°
【对应训练】
1.如图,将 ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E的度数为( B )
A.102° B.112°
C.122° D.92°
2.【2023·宜昌】如图,小宇将一张平行四边形纸片折叠,使点A落在长边CD上的点A'处,并得到折痕DE,小宇测得长边CD=8,则四边形A'EBC的周长为 .
【答案】16
3.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F.若∠B=80°,∠ACE=2∠ECD.FC=a,FD=b,则 ABCD的周长为 .
【答案】4a+2b
4.如图,在平行四边形ABCD中,已知AD=,∠DAB=45°,AB=3,如果把该平行四边形折叠,点A恰好与点C重合,求折痕EF的长.
解:如图,过A点作CD的垂线,与CD的延长线交于G点,连接AE,CF,∵AD=,∠DAB=45°,∴△ADG为等腰直角三角形,AG=GD=1,
设AE=x,由折叠可知,EC=AE=x,DE=3-x,在Rt△AGE中,由勾股定理得:AG2+GE2=AE2,即12+(1+3-x)2=x2,解得x=;在Rt△AGC中,由勾股定理得:AC===,∵EF⊥AC,根据菱形AECF计算面积的方法可知,AG·EC=EF·AC,即1×=EF×,解得EF=
二、矩形的折叠
【例2】如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O,若AE=5,BF=3,求AC的长.
分析:先由平行四边形的性质和折叠的性质求得AE=AF=5,再由折叠得FC=AF,最后由勾股定理即可求出 AC的长.
解:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,AB=CD,∴∠EFC=∠AEF,由折叠,得∠EFC=∠AFE,∴∠AFE=∠AEF,∴AE=AF=5,由折叠得,FC=AF,OA=OC,∴BC=3+5=8,在Rt△ABF中,AB==4,在Rt△ABC中,AC==4
【对应训练】
5.如图,在矩形ABCD中,点M在AB边上,把△BCM沿直线CM折叠,使点B落在AD边上的点E处,连接EC,过点B作BF⊥EC,垂足为F,若CD=1,CF=2,则线段AE的长为( A )
A.-2 B.-1
C. D.
6.【2023·牡丹江】在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( C )
A.3 B. C.2 D.1
7.如图,将长、宽分别为12 cm,3 cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)的面积为( A )
A.(36-6 ) cm2 B.(36-12 ) cm2 C.24 cm2 D.36 cm2
8.如图,矩形ABCD中,AB=8 cm,BC=16 cm,如果将该矩形沿对角线BD折叠,点C落在点C′处,BC′交AD于点E,求图中阴影部分的面积.
解:∵四边形ABCD是矩形,
∴AB=CD=8 cm,BC=AD=16 cm,
AD∥BC,∠A=90°,
∴∠EDB=∠CBD.
由折叠可知,∠EBD=∠CBD,
∴∠EBD=∠EDB,∴BE=DE.
设DE为x cm,则AE=(16-x) cm,BE=x cm,
由勾股定理,得AB2+AE2=BE2.
∴64+(16-x)2=x2,解得x=10.
∴DE=10 cm,
∴阴影部分的面积为×DE×AB=40(cm2).
9.如图,将一张矩形纸片ABCD先沿着BE折叠,使点A刚好落在CD边上点G处,再沿着BF折叠(其中点F为CG上的一点),使点C恰好落在BG上点H处,连接AG,若S△BCF∶S△BGF=3∶5,AB=15,求AG的长.
解:∵四边形ABCD是矩形,∴∠D=∠C=90°,DC=AB=15,
∴FC⊥BC.由折叠得GB=AB=15,FC=FH,
∠C=∠BHF=90°,∴FH⊥GB.
∵S△BCF∶S△BGF=3∶5,∴∶=3∶5,
∴BC∶GB=3∶5,∴BC=GB=×15=9,∴AD=BC=9,
∴CG===12,∴DG=DC-CG=15-12=3,
∴AG===3.
10.(1)将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,如图①.求证:四边形AEA'D是正方形;
(2)将图①中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,如图②.线段MC'与ME是否相等?若相等,请给出证明;若不等,请说明理由.
解:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°.
∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,
∴AD=A'D,AE=A'E,∠ADE=∠A'DE=45°.
∵AB∥CD,∴∠AED=∠A'DE=∠ADE.
∴AD=AE.∴AD=AE=A'E=A’D.
∴四边形AEA'D是菱形.
∵∠A=90°,∴四边形AEA'D是正方形.
(2)MC'=ME.
证明:如图②,连接C'E,由(1)知,AD=AE,
∵四边形ABCD是矩形,
∴AD=BC,∠EAC'=∠B=90°.
由折叠知,B'C'=BC,∠B=∠B',
∴AE=B'C',∠EAC'=∠B'.
在Rt△EC'A和Rt△C'EB'中,
∴Rt△EC'A≌Rt△C'EB'(HL).
∴∠C'EA=∠EC'B'.∴MC'=ME.
三、菱形的折叠
【例3】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G(不与B,D重合),折痕为EF,若DG=2,BG=6,求BE的长.
分析:由菱形的性质易知△ABD为等边三角形,从而得到AB=BD=8,由折叠的性质可知,EG=EA,作EH⊥BD于H,设BE=x,根据勾股定理列方程求出x即可.
解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意,得BD=DG+BG=8. ∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8-x,在Rt△EHB中,∵∠ABD=60°,∠BHE=90°,∴BH=x,EH===x,在Rt△EHG中,EG2=EH2+GH2,即(8-x)2=(x)2+(6-x)2,解得x=2.8,即BE=2.8
【对应训练】
11.如图,将菱形ABCD的边AD以直线AN为对称轴翻折至AM,使点C恰好落在AM上.若此时CM=CN,则∠D的度数为( D )
A.30° B.54° C.45° D.36°
12.如图,已知四边形ABCD是边长为6的菱形,且∠BAD=120°,点E,F分别在AB,BC边上,将菱形沿EF折叠,点B正好落在AD边的点G处,若EG⊥AC,则FG的长为( C )
A.3 B.6 C.3 D.3
13.如图,菱形ABCD的边长为4,∠A=60°,将菱形沿EF折叠,顶点C恰好落在AB边的中点G处,求BF的长.
解:过F作FH⊥AB,交AB的延长线于点H,∵∠A=60°,AD∥BC,∴∠HBF=60°,∠BFH=30°,设BH=x,则BF=2x,CF=4-2x=GF,FH=x,∵G是AB的中点,∴BG=2,GH=2+x,Rt△FGH中,FH2+GH2=GF2,∴(x)2+(2+x)2=(4-2x)2,解得x=0.6,∴BF=2x=1.2
14.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF.若菱形的边长为2,∠A=120°,求EF的长.
解:如图,连接BD,AC,则O为AC与BD的交点.
∵四边形ABCD是菱形,
∴AC⊥BD,AC平分∠BAD.
∵∠BAD=120°,∴∠BAC=60°.
∴∠ABO=90°-60°=30°.
∴AO=AB=×2=1.
设OA与EF的交点为G,由折叠知,
AG=AO=,OA⊥EF,
∴由勾股定理,得EG=,
∴EF=2EG=.
四、正方形的折叠
【例4】如图,四边形ABCD为正方形,点E是BC的中点,将正方形ABCD沿AE折叠,得到点B的对应点为点F,延长EF交线段DC于点P,若AB=6,求DP的长.
分析:由正方形的性质和折叠的性质可证明Rt△AFP≌Rt△ADP,所以PF=PD,设PF=PD=x,由勾股定理列方程求出x即可.
解:连接AP,∵四边形ABCD为正方形,∴AB=BC=AD=6,∠B=∠C=∠D=90°,点E是BC的中点,∴BE=CE=3,由翻折可知:AF=AB,EF=BE=3,∠AFE=∠B=90°,∴AD=AF,∠AFP=∠D=90°,在Rt△AFP和Rt△ADP中, ∴Rt△AFP≌Rt△ADP(HL),∴PF=PD,设PF=PD=x,则CP=CD-PD=6-x,EP=EF+FP=3+x,在Rt△PEC中,根据勾股定理得:EP2=EC2+CP2,∴(3+x)2=32+(6-x)2,解得x=2.即DP的长度为2
【对应训练】
15.如图,正方形ABCD的边长为4,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=3∶1,则线段CH的长是( B )
A.3 B. C.1 D.2
16.如图,正方形纸片ABCD的边长为4,E,F,H分别是边BC,CD,AB上的一点,将纸片沿FH折叠,使点D恰好落在BC边的中点E处,点A的对应点为P,则折痕FH的长为 .
【答案】2
17.如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
【答案】
18.如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,求BF2的值.
解:过点F作FG⊥BC交于G点,
由折叠可知DE=EF,AD=AF,∠D=∠EFA=90°,
设正方形的边长为x,∵EF=2,
∴DE=2,EC=x-2,AC=x,
在Rt△EFC中,EC2=FE2+FC2,∴(x-2)2=4+(x-x)2,
解得x=2+2,∴FC=x-x=2,
∵∠ACB=45°,∴由勾股定理得FG=CG=,
∴BG=+2,在Rt△BFG中,
BF2=BG2+GF2=(+2)2+2=8+4.
19.如图,正方形ABCD中,点E在边CD上,且CD=3DE.将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,连接AG,CF.
(1)求∠EAG的度数;
(2)求证:AG∥CF;
(3)若AB=6,则△GCF的面积等于 .
(1)解:∠EAG=45°.
(2)证明:设BG=FG=x,DE=EF=a,则BC=CD=3a,CE=2a.
在Rt△ECG中,由勾股定理,得CG2+CE2=EG2,
即(3a-x)2+(2a)2=(x+a)2,解得x=a.
∴FG=BG=GC,∴∠GCF=∠GFC,
∵∠BGF=∠GCF+∠GFC=2∠GCF,∠BGF=2∠BGA,
∴∠GCF=∠BGA,∴AG∥CF.
(3)
20.如图,将一块边长为9的正方形纸片ABCD的顶点A折叠至DC边上的点E处,使DE=3,折痕为PQ,连接AE交PQ于点M.
求:(1)PA的长;
(2)PM的长.
解:(1)如图所示,连接PE,由折叠可得,PQ垂直平分AE,
∴PA=PE,
设AP=PE=x,则PD=9-x,Rt△DEP中,DE2+DP2=PE2,即32+(9-x)2=x2,
解得x=5,∴AP=5.
(2)Rt△ADE中,AE===3,
∴AM=AE= ,
由折叠可得PQ⊥AE,
∴Rt△APM中,
PM===.
