RJ数学八下专题课堂(六) 构造三角形的中位线(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(六) 构造三角形的中位线(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 10:30:51 | ||
图片预览

文档简介
RJ数学八下专题课堂(六) 构造三角形的中位线
一、已知两边中点,连接构造三角形中位线
【例1】如图,在四边形ABCD中,E,F分别是边AB,AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,求∠ADC的度数.
分析: 连接BD,根据勾股定理逆定理可求出∠BDC=90°,由三角形的中位线定理可求出∠BDA=∠AFE=50°,从而可得出∠ADC的度数.
【对应训练】
1.如图,在边长为4的等边△ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.
(1)求EF的长;
(2)求DG的长.
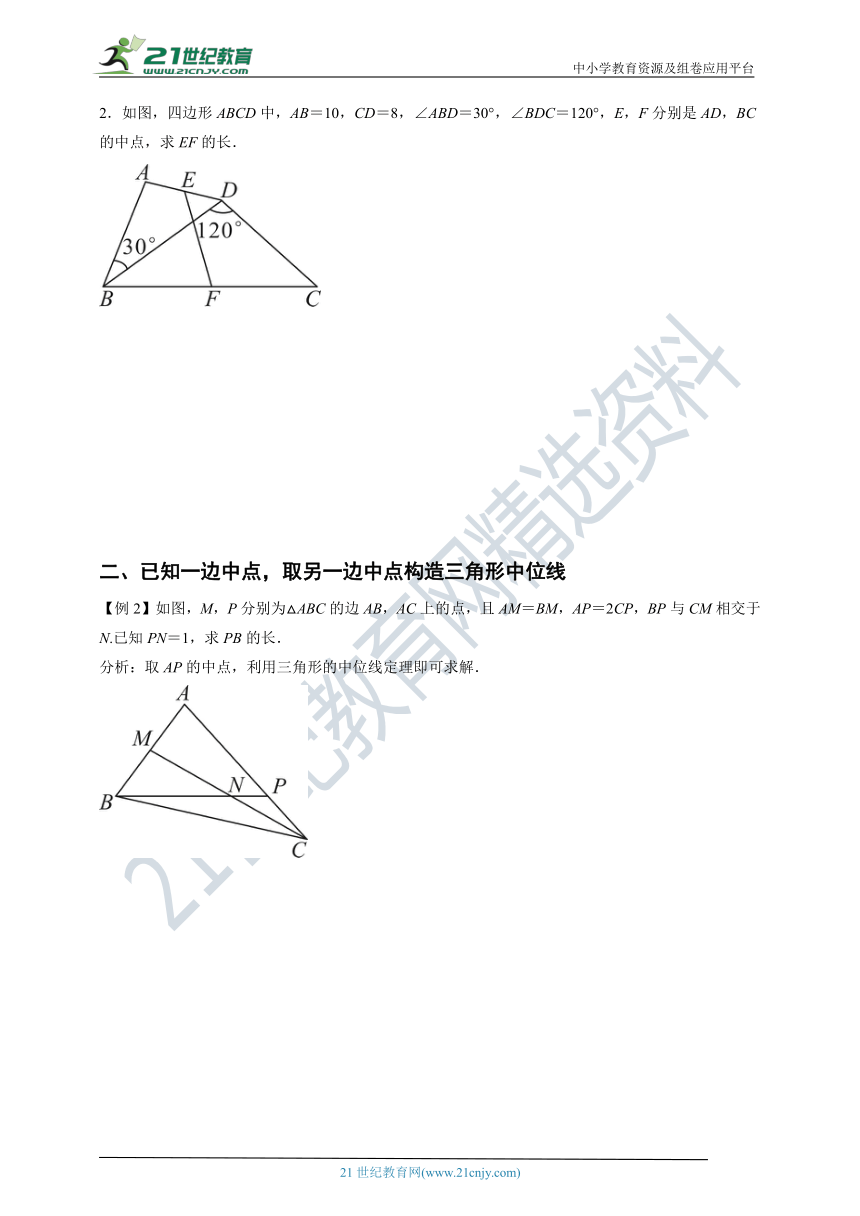
2.如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,求EF的长.
二、已知一边中点,取另一边中点构造三角形中位线
【例2】如图,M,P分别为△ABC的边AB,AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,求PB的长.
分析:取AP的中点,利用三角形的中位线定理即可求解.
【对应训练】
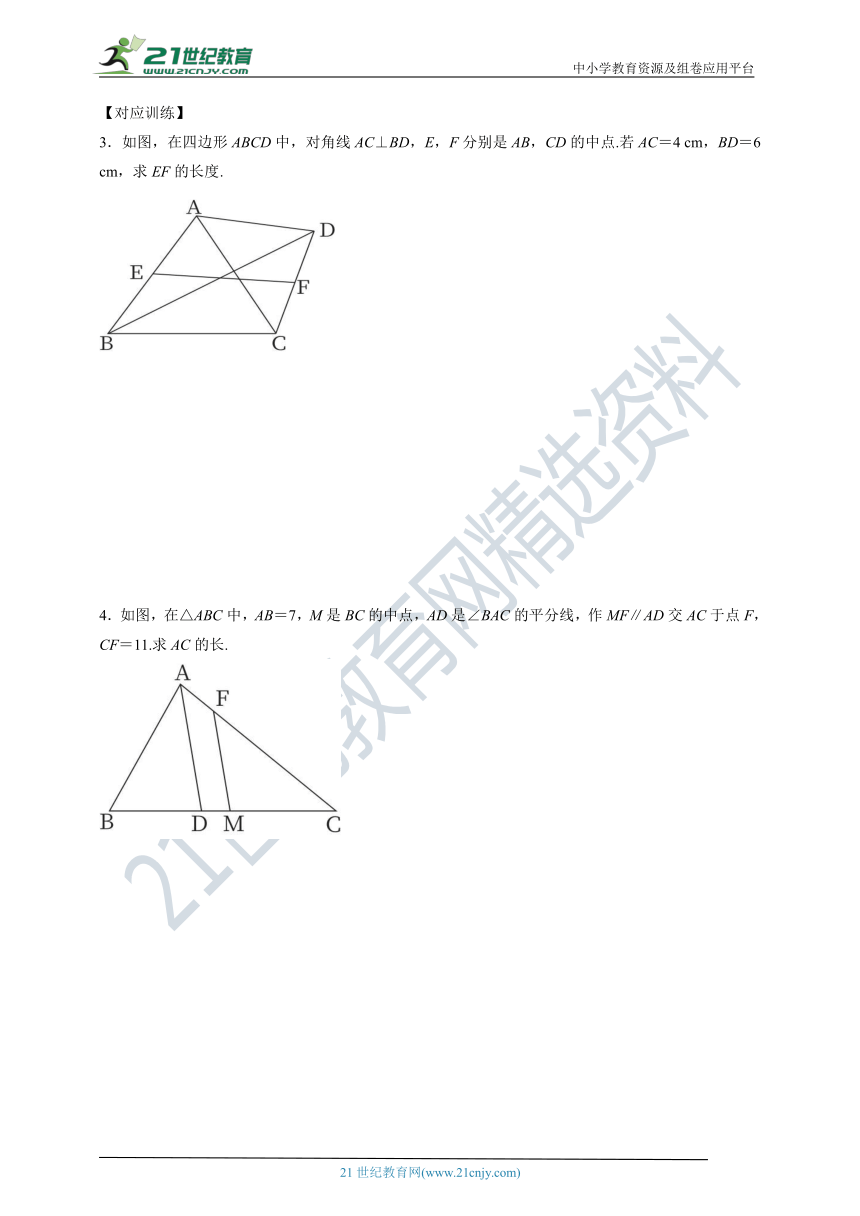
3.如图,在四边形ABCD中,对角线AC⊥BD,E,F分别是AB,CD的中点.若AC=4 cm,BD=6 cm,求EF的长度.
4.如图,在△ABC中,AB=7,M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于点F,CF=11.求AC的长.
三、已知一边中点,延长另一边构造三角形中位线
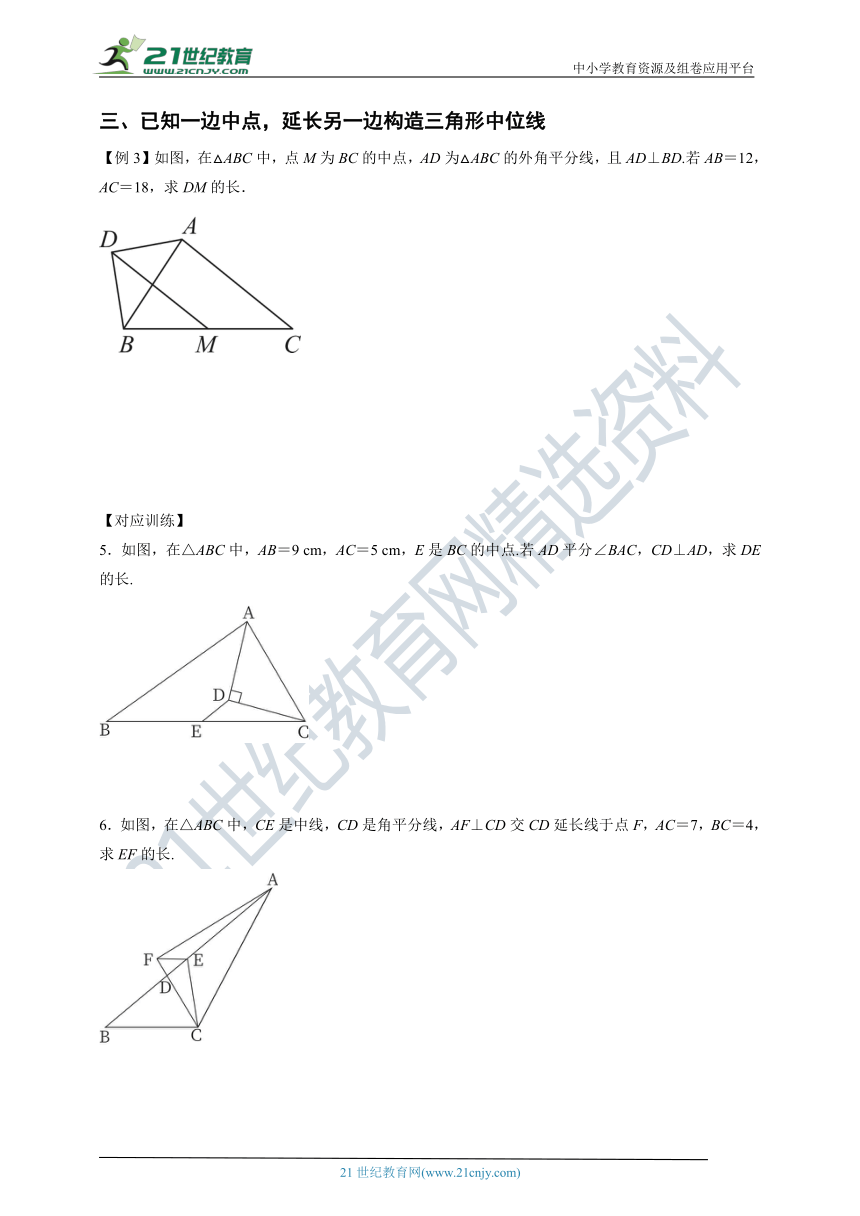
【例3】如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD.若AB=12,AC=18,求DM的长.
【对应训练】
5.如图,在△ABC中,AB=9 cm,AC=5 cm,E是BC的中点.若AD平分∠BAC,CD⊥AD,求DE的长.
6.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD延长线于点F,AC=7,BC=4,求EF的长.
四、已知四边形对边的中点,取对角线中点构造三角形中位线
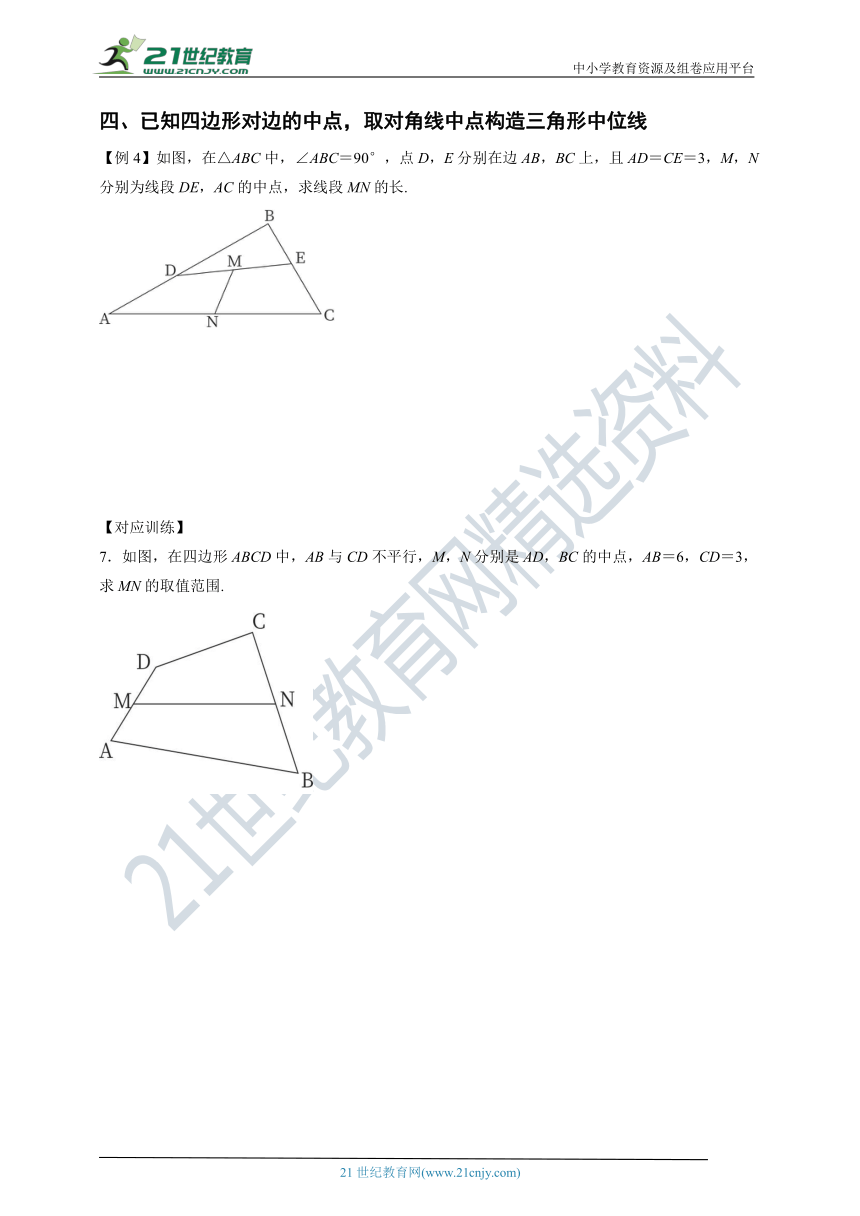
【例4】如图,在△ABC中,∠ABC=90°,点D,E分别在边AB,BC上,且AD=CE=3,M,N分别为线段DE,AC的中点,求线段MN的长.
【对应训练】
7.如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,求MN的取值范围.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、已知两边中点,连接构造三角形中位线
【例1】如图,在四边形ABCD中,E,F分别是边AB,AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,求∠ADC的度数.
分析: 连接BD,根据勾股定理逆定理可求出∠BDC=90°,由三角形的中位线定理可求出∠BDA=∠AFE=50°,从而可得出∠ADC的度数.
解:连接BD,∵点E,F分别是边AB,AD的中点,EF=6,∴EF∥BD,BD=2EF=12,∴∠ADB=∠AFE=50°,在△BDC中,BD2+CD2=122+92=225,BC2=225,∴BD2+CD2=BC2,∴∠BDC=90°,∴∠ADC=90°+50°=140°
【对应训练】
1.如图,在边长为4的等边△ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.
(1)求EF的长;
(2)求DG的长.
解:(1)EF=.
(2)连接DE.
∵在边长为4的等边△ABC中,D,E分别为AB,BC的中点,
∴DE=2且DE∥AC.
∵EF⊥AC,∴DE⊥EF,即∠DEF=90°.
∵G为EF的中点,∴EG=,
∴DG=.
2.如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,求EF的长.
解:如图,取BD的中点P,连接EP,FP.∵E,F分别是AD,BC的中点,AB=10,CD=8,∴PE∥AB,且PE=AB=5,PF∥CD且PF=CD=4.又∵∠ABD=30°,∠BDC=120°,∴∠EPD=∠ABD=30°,∠DPF=180°-∠BDC=60°,∴∠EPF=∠EPD+∠DPF=90°,∴在直角△EPF中,由勾股定理得到:EF===
二、已知一边中点,取另一边中点构造三角形中位线
【例2】如图,M,P分别为△ABC的边AB,AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,求PB的长.
分析:取AP的中点,利用三角形的中位线定理即可求解.
解:如图所示,取AP的中点D,连接MD,
∵AP=2CP,∴AD=DP=CP,∵AM=BM,
∴DM是△ABP的中位线,∴DM∥BP,BP=2DM,
∴PN是△CDM的中位线,
∴DM=2PN=2,∴BP=2DM=2×2=4
【对应训练】
3.如图,在四边形ABCD中,对角线AC⊥BD,E,F分别是AB,CD的中点.若AC=4 cm,BD=6 cm,求EF的长度.
解:取BC的中点H,连接EH,FH.
∵E,F分别是AB,CD的中点,
∴EH==2 cm,FH==3 cm,EH∥AC,FH∥BD.
∵AC⊥BD,∴EH⊥FH,即∠EHF=90°,
∴EF= cm.
4.如图,在△ABC中,AB=7,M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于点F,CF=11.求AC的长.
解:取AC的中点N,连接MN.
∵M,N分别是BC,AC的中点,
∴MN=,MN∥AB,NC=.
易得∠MNC=2∠DAC.
∵MF∥AD,∴∠MFN=∠DAC,
∴∠MFN=∠FMN,∴FN=MN=.
∵CF=11,∴NC=CF-FN=,
∴AC=2NC=15.
三、已知一边中点,延长另一边构造三角形中位线
【例3】如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD.若AB=12,AC=18,求DM的长.
解:延长BD交CA的延长线交于点E,∵AD为△ABC的外角平分线,∴∠EAD=∠BAD,在△EAD和△BAD中,∴△EAD≌△BAD(ASA),∴AE=AB=12,BD=DE,∴EC=AE+AC=30,∵BM=MC,BD=DE,∴DM是△EBC的中位线,∴DM=EC=15
【对应训练】
5.如图,在△ABC中,AB=9 cm,AC=5 cm,E是BC的中点.若AD平分∠BAC,CD⊥AD,求DE的长.
解:延长CD交AB于点F.
易证△ADF≌△ADC(ASA),
∴AF=AC=5,CD=FD,∴BF=AB-AF=4.
∵CD=FD,E为BC的中点,
∴DE==2 cm.
6.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD延长线于点F,AC=7,BC=4,求EF的长.
解:延长AF,CB交于点G.
易证△ACF≌△GCF(ASA),
∴CG=AC=7,AF=GF,
∴BG=CG-BC=3.
∵AE=BE,AF=GF,
∴EF==1.5.
四、已知四边形对边的中点,取对角线中点构造三角形中位线
【例4】如图,在△ABC中,∠ABC=90°,点D,E分别在边AB,BC上,且AD=CE=3,M,N分别为线段DE,AC的中点,求线段MN的长.
解:连接CD,取CD的中点H,连接MH,NH.
∵M,H分别为DE,CD的中点,
∴MH=,MH∥CE.
同理可得NH=,NH∥AD.
∵∠ABC=90°,即CE⊥AD,
∴MH⊥NH,即∠MHN=90°,
∴MN=.
【对应训练】
7.如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,求MN的取值范围.
解:连接BD,取BD的中点E,连接ME,NE.
∵M是AD的中点,E是BD的中点,
∴ME==3.
同理可得NE==1.5,
在△MNE中,3-1.5<MN<3+1.5,
即1.5<MN<4.5.
一、已知两边中点,连接构造三角形中位线
【例1】如图,在四边形ABCD中,E,F分别是边AB,AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,求∠ADC的度数.
分析: 连接BD,根据勾股定理逆定理可求出∠BDC=90°,由三角形的中位线定理可求出∠BDA=∠AFE=50°,从而可得出∠ADC的度数.
【对应训练】
1.如图,在边长为4的等边△ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.
(1)求EF的长;
(2)求DG的长.
2.如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,求EF的长.
二、已知一边中点,取另一边中点构造三角形中位线
【例2】如图,M,P分别为△ABC的边AB,AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,求PB的长.
分析:取AP的中点,利用三角形的中位线定理即可求解.
【对应训练】
3.如图,在四边形ABCD中,对角线AC⊥BD,E,F分别是AB,CD的中点.若AC=4 cm,BD=6 cm,求EF的长度.
4.如图,在△ABC中,AB=7,M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于点F,CF=11.求AC的长.
三、已知一边中点,延长另一边构造三角形中位线
【例3】如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD.若AB=12,AC=18,求DM的长.
【对应训练】
5.如图,在△ABC中,AB=9 cm,AC=5 cm,E是BC的中点.若AD平分∠BAC,CD⊥AD,求DE的长.
6.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD延长线于点F,AC=7,BC=4,求EF的长.
四、已知四边形对边的中点,取对角线中点构造三角形中位线
【例4】如图,在△ABC中,∠ABC=90°,点D,E分别在边AB,BC上,且AD=CE=3,M,N分别为线段DE,AC的中点,求线段MN的长.
【对应训练】
7.如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,求MN的取值范围.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、已知两边中点,连接构造三角形中位线
【例1】如图,在四边形ABCD中,E,F分别是边AB,AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,求∠ADC的度数.
分析: 连接BD,根据勾股定理逆定理可求出∠BDC=90°,由三角形的中位线定理可求出∠BDA=∠AFE=50°,从而可得出∠ADC的度数.
解:连接BD,∵点E,F分别是边AB,AD的中点,EF=6,∴EF∥BD,BD=2EF=12,∴∠ADB=∠AFE=50°,在△BDC中,BD2+CD2=122+92=225,BC2=225,∴BD2+CD2=BC2,∴∠BDC=90°,∴∠ADC=90°+50°=140°
【对应训练】
1.如图,在边长为4的等边△ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.
(1)求EF的长;
(2)求DG的长.
解:(1)EF=.
(2)连接DE.
∵在边长为4的等边△ABC中,D,E分别为AB,BC的中点,
∴DE=2且DE∥AC.
∵EF⊥AC,∴DE⊥EF,即∠DEF=90°.
∵G为EF的中点,∴EG=,
∴DG=.
2.如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,求EF的长.
解:如图,取BD的中点P,连接EP,FP.∵E,F分别是AD,BC的中点,AB=10,CD=8,∴PE∥AB,且PE=AB=5,PF∥CD且PF=CD=4.又∵∠ABD=30°,∠BDC=120°,∴∠EPD=∠ABD=30°,∠DPF=180°-∠BDC=60°,∴∠EPF=∠EPD+∠DPF=90°,∴在直角△EPF中,由勾股定理得到:EF===
二、已知一边中点,取另一边中点构造三角形中位线
【例2】如图,M,P分别为△ABC的边AB,AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,求PB的长.
分析:取AP的中点,利用三角形的中位线定理即可求解.
解:如图所示,取AP的中点D,连接MD,
∵AP=2CP,∴AD=DP=CP,∵AM=BM,
∴DM是△ABP的中位线,∴DM∥BP,BP=2DM,
∴PN是△CDM的中位线,
∴DM=2PN=2,∴BP=2DM=2×2=4
【对应训练】
3.如图,在四边形ABCD中,对角线AC⊥BD,E,F分别是AB,CD的中点.若AC=4 cm,BD=6 cm,求EF的长度.
解:取BC的中点H,连接EH,FH.
∵E,F分别是AB,CD的中点,
∴EH==2 cm,FH==3 cm,EH∥AC,FH∥BD.
∵AC⊥BD,∴EH⊥FH,即∠EHF=90°,
∴EF= cm.
4.如图,在△ABC中,AB=7,M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于点F,CF=11.求AC的长.
解:取AC的中点N,连接MN.
∵M,N分别是BC,AC的中点,
∴MN=,MN∥AB,NC=.
易得∠MNC=2∠DAC.
∵MF∥AD,∴∠MFN=∠DAC,
∴∠MFN=∠FMN,∴FN=MN=.
∵CF=11,∴NC=CF-FN=,
∴AC=2NC=15.
三、已知一边中点,延长另一边构造三角形中位线
【例3】如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD.若AB=12,AC=18,求DM的长.
解:延长BD交CA的延长线交于点E,∵AD为△ABC的外角平分线,∴∠EAD=∠BAD,在△EAD和△BAD中,∴△EAD≌△BAD(ASA),∴AE=AB=12,BD=DE,∴EC=AE+AC=30,∵BM=MC,BD=DE,∴DM是△EBC的中位线,∴DM=EC=15
【对应训练】
5.如图,在△ABC中,AB=9 cm,AC=5 cm,E是BC的中点.若AD平分∠BAC,CD⊥AD,求DE的长.
解:延长CD交AB于点F.
易证△ADF≌△ADC(ASA),
∴AF=AC=5,CD=FD,∴BF=AB-AF=4.
∵CD=FD,E为BC的中点,
∴DE==2 cm.
6.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD延长线于点F,AC=7,BC=4,求EF的长.
解:延长AF,CB交于点G.
易证△ACF≌△GCF(ASA),
∴CG=AC=7,AF=GF,
∴BG=CG-BC=3.
∵AE=BE,AF=GF,
∴EF==1.5.
四、已知四边形对边的中点,取对角线中点构造三角形中位线
【例4】如图,在△ABC中,∠ABC=90°,点D,E分别在边AB,BC上,且AD=CE=3,M,N分别为线段DE,AC的中点,求线段MN的长.
解:连接CD,取CD的中点H,连接MH,NH.
∵M,H分别为DE,CD的中点,
∴MH=,MH∥CE.
同理可得NH=,NH∥AD.
∵∠ABC=90°,即CE⊥AD,
∴MH⊥NH,即∠MHN=90°,
∴MN=.
【对应训练】
7.如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,求MN的取值范围.
解:连接BD,取BD的中点E,连接ME,NE.
∵M是AD的中点,E是BD的中点,
∴ME==3.
同理可得NE==1.5,
在△MNE中,3-1.5<MN<3+1.5,
即1.5<MN<4.5.
