RJ数学八下专题课堂(七) 特殊平行四边形的性质与判定(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(七) 特殊平行四边形的性质与判定(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 09:31:46 | ||
图片预览


文档简介
RJ数学八下专题课堂(七) 特殊平行四边形的性质与判定
一、矩形的性质与判定
【例1】如图,M是矩形ABCD的边AD的中点,P是BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件________________时,四边形PEMF为矩形.
分析:根据已知条件,矩形的性质和判定,欲证明四边形PEMF为矩形,只需证明∠BMC=90°,易得AB=BC时,满足∠BMC=90°的条件.
【对应训练】
1.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
3.【2022·吉林】如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF=_________.
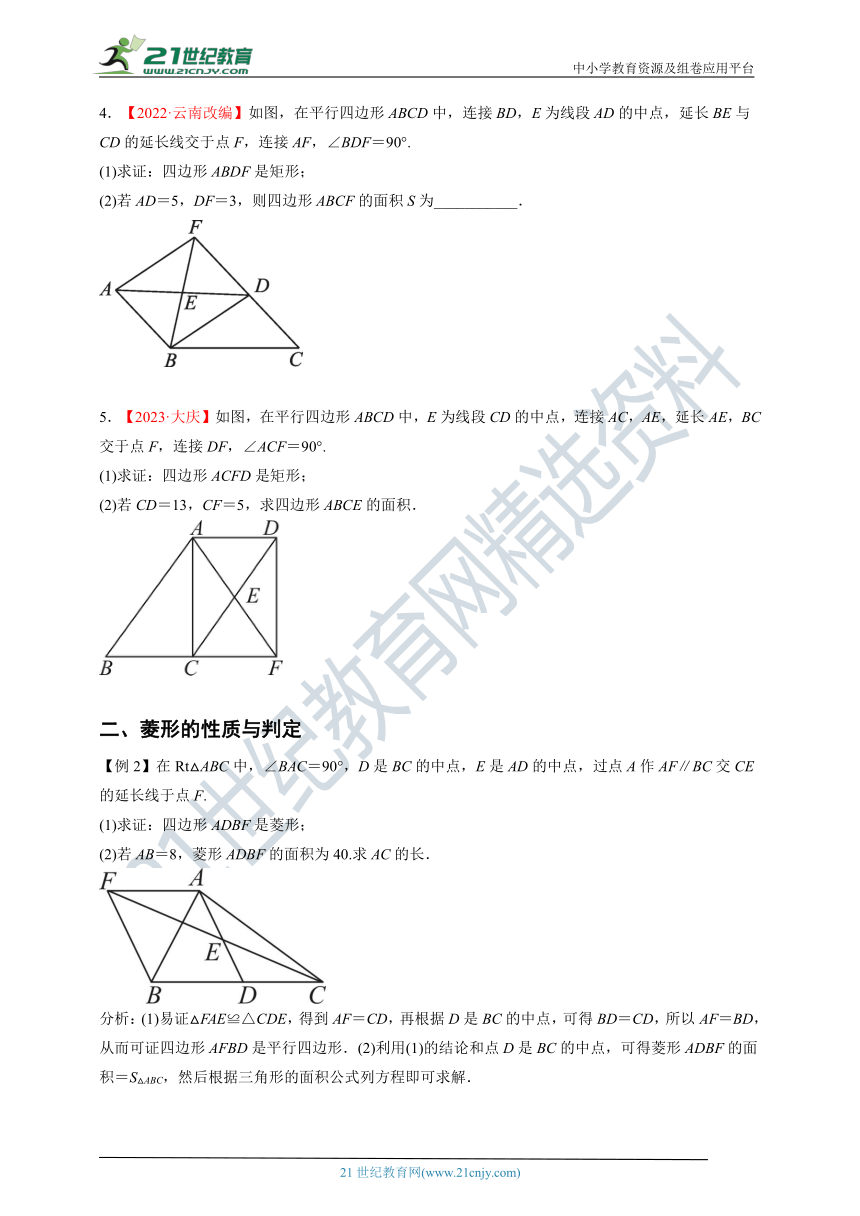
4.【2022·云南改编】如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,则四边形ABCF的面积S为___________.
5.【2023·大庆】如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
二、菱形的性质与判定
【例2】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
分析:(1)易证△FAE≌△CDE,得到AF=CD,再根据D是BC的中点,可得BD=CD,所以AF=BD,从而可证四边形AFBD是平行四边形.(2)利用(1)的结论和点D是BC的中点,可得菱形ADBF的面积=S△ABC,然后根据三角形的面积公式列方程即可求解.
【对应训练】
6.把一个长方形的纸片按如图所示折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是________.
8.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
9.如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连接AF.
(1)求证:FB=AO;
(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.
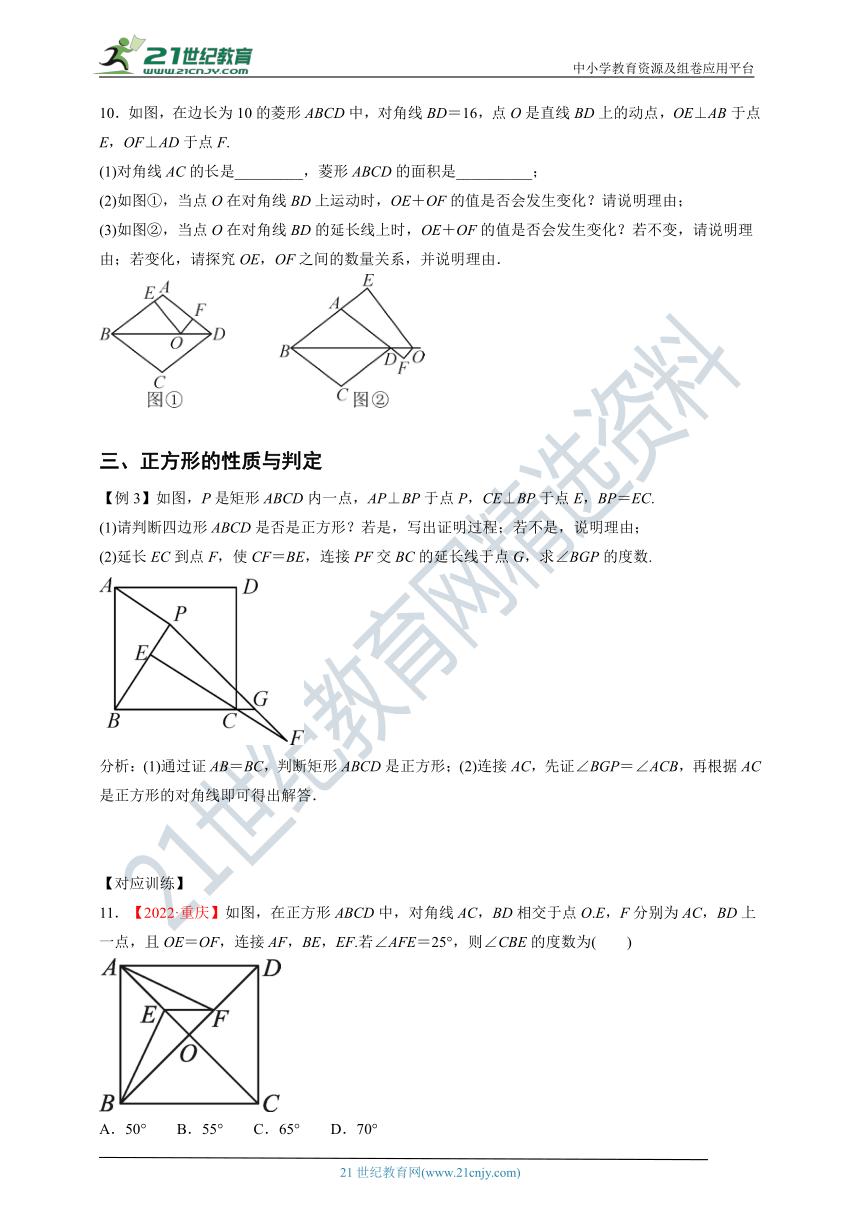
10.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)对角线AC的长是_________,菱形ABCD的面积是__________;
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系,并说明理由.
三、正方形的性质与判定
【例3】如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.
(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
分析:(1)通过证AB=BC,判断矩形ABCD是正方形;(2)连接AC,先证∠BGP=∠ACB,再根据AC是正方形的对角线即可得出解答.
【对应训练】
11.【2022·重庆】如图,在正方形ABCD中,对角线AC,BD相交于点O.E,F分别为AC,BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( )
A.50° B.55° C.65° D.70°
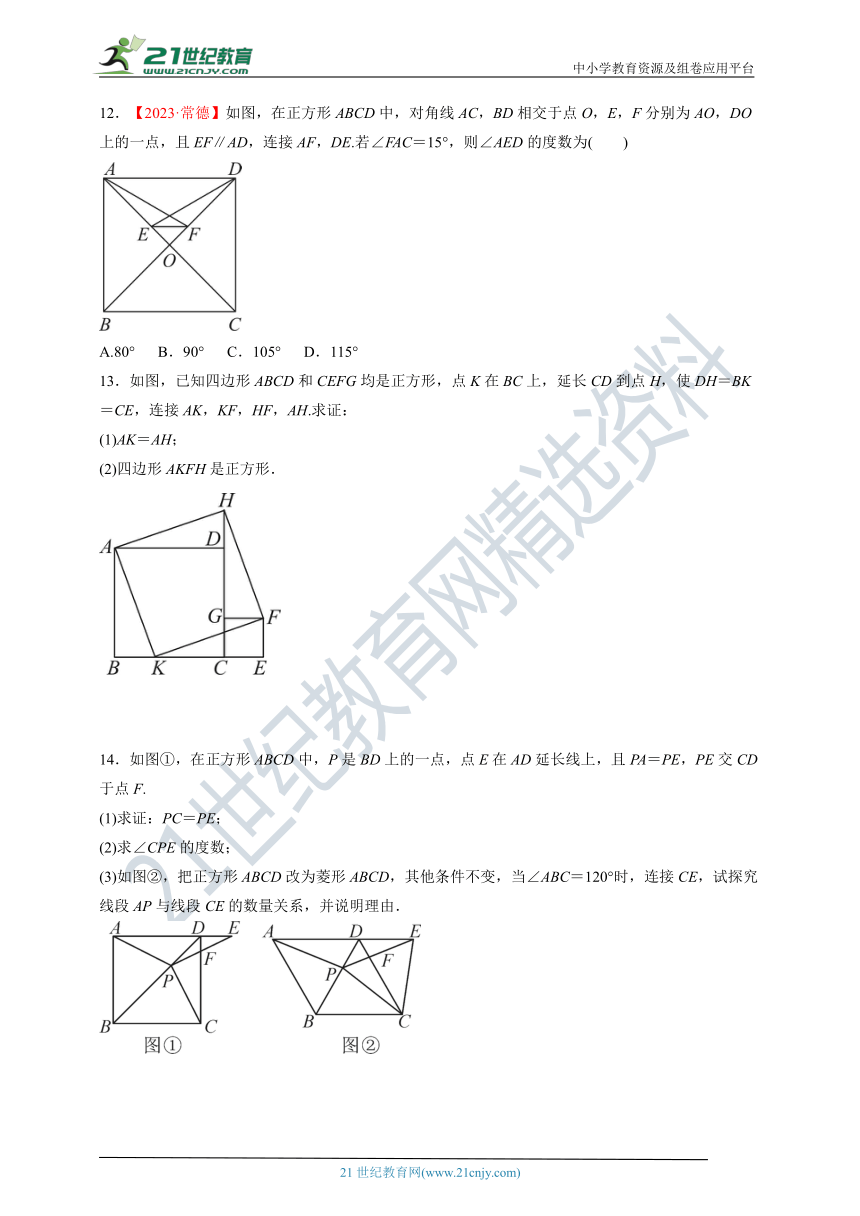
12.【2023·常德】如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( )
A.80° B.90° C.105° D.115°
13.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.求证:
(1)AK=AH;
(2)四边形AKFH是正方形.
14.如图①,在正方形ABCD中,P是BD上的一点,点E在AD延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、矩形的性质与判定
【例1】如图,M是矩形ABCD的边AD的中点,P是BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件________________时,四边形PEMF为矩形.
分析:根据已知条件,矩形的性质和判定,欲证明四边形PEMF为矩形,只需证明∠BMC=90°,易得AB=BC时,满足∠BMC=90°的条件.
【答案】AB=BC
【对应训练】
1.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( A )
A.4 B.4 C.10 D.8
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( C )
A.6 B.8 C.10 D.12
3.【2022·吉林】如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF=_________.
【答案】
4.【2022·云南改编】如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,则四边形ABCF的面积S为___________.
解:(1)∵四边形ABCD是平行四边形,∴BA∥CD,∴∠BAE=∠FDE,∵点E是AD的中点,∴AE=DE,∵∠BEA=∠FED,△BEA≌△FED(ASA),∴EF=EB,又∵AE=DE,∴四边形ABDF是平行四边形,∵∠BDF=90°,∴四边形ABDF是矩形
(2)18
5.【2023·大庆】如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADE=∠FCE,∠DAE=∠CFE,∵E为线段CD的中点,∴DE=CE,∴△ADE≌△FCE(AAS),∴AE=FE,∴四边形ACFD是平行四边形,∵∠ACF=90°,∴四边形ACFD是
(2)∵四边形ACFD是矩形,∴∠CFD=90°,AC=DF,∵CD=13,CF=5,∴DF===12,∵△ADE≌△FCE,∵△CEF的面积=△ACF的面积=××5×12=15,平行四边形ABCD的面积=BC·AC=5×12=60,∴四边形ABCE的面积=平行四边形ABCD的面积-△ADE的面积=60-15=45
二、菱形的性质与判定
【例2】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
分析:(1)易证△FAE≌△CDE,得到AF=CD,再根据D是BC的中点,可得BD=CD,所以AF=BD,从而可证四边形AFBD是平行四边形.(2)利用(1)的结论和点D是BC的中点,可得菱形ADBF的面积=S△ABC,然后根据三角形的面积公式列方程即可求解.
解:(1)∵AF∥BC,∴∠AFC=∠FCD,∠FAE=∠CDE,∵点E是AD的中点,∴AE=DE,∴△FAE≌△CDE(AAS),∴AF=CD,∵点D是BC的中点,∴BD=CD,∴AF=BD,∴四边形AFBD是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=BD=BC,∴四边形ADBF是菱形
(2)∵四边形ADBF是菱形,∴菱形ADBF的面积=2S△ABD,∵点D是BC的中点,∴△ABC的面积=2S△ABD,∴菱形ADBF的面积=S△ABC=40,∴AB·AC=40,∴×8AC=40,∴AC=10,∴AC的长为10
【对应训练】
6.把一个长方形的纸片按如图所示折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( D )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是________.
【答案】16
8.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
证明:(1)∵四边形ABCD是菱形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF,在△ABE和△CDF中,∴△ABE≌△CDF(SAS)
(2)如图,连接BD,交AC于O,∵四边形ABCD是菱形,∴BD⊥AC,AO=CO,BO=DO,∵AE=CF,∴EO=FO,∴四边形BEDF是平行四边形,又∵BD⊥EF,∴平行四边形BEDF是菱形
9.如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连接AF.
(1)求证:FB=AO;
(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.
解:(1)∵BF∥AC,∴∠BFE=∠OCE,又∵BE=OE,∠BEF=∠OEC,∴△BEF≌△OEC(AAS),∴BF=OC,又∵OC=AO,∴FB=AO
(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由:∵FB∥AO,且FB=AO,∴四边形AFBO是平行四边形,∵平行四边形ABCD是矩形,∴AC=BD,OA=AC,OB=BD,∴OA=OB,∴四边形AFBO是菱形
10.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)对角线AC的长是_________,菱形ABCD的面积是__________;
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系,并说明理由.
解:(1)12 96
(2)OE+OF的值不变.理由:连接AO,AC,AC交BD于点G,则S△ABD=S△ABO+S△ADO,∴BD·AG=AB·OE+AD·OF,即×16×6=×10OE+×10OF,可得OE+OF=9.6,即OE+OF的值不变
(3)变化,同(2)方法可求得OE-OF=9.6
三、正方形的性质与判定
【例3】如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.
(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
分析:(1)通过证AB=BC,判断矩形ABCD是正方形;(2)连接AC,先证∠BGP=∠ACB,再根据AC是正方形的对角线即可得出解答.
解:(1)四边形ABCD是正方形.证明:∵四边形ABCD是矩形,∴∠ABC=90°,即∠ABP+∠PBC=90°,∵AP⊥BP,∴∠ABP+∠PAB=90°,∴∠PBC=∠PAB,∵CE⊥BP,∴∠APB=∠BEC=90°,又∵BP=CE,∴△ABP≌△BCE(AAS),∴AB=BC,∴矩形ABCD是正方形
(2)连接AC,∵△ABP≌△BCE,∴AP=BE,∵BE=CF,∴AP=CF,∵AP⊥BP,CE⊥BP,∴∠APB=∠CEP=90°,∴AP∥CF,∴四边形ACFP是平行四边形,∴AC∥PF,∴∠ACB=∠BGP,∵四边形ABCD是正方形,AC是对角线,∴∠ACB=45°,∴∠BGP=45°
【对应训练】
11.【2022·重庆】如图,在正方形ABCD中,对角线AC,BD相交于点O.E,F分别为AC,BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( C )
A.50° B.55° C.65° D.70°
12.【2023·常德】如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( C )
A.80° B.90° C.105° D.115°
13.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.求证:
(1)AK=AH;
(2)四边形AKFH是正方形.
证明:(1)∵四边形ABCD和CEFG都是正方形,∴AB=AD=DC=BC,GC=EC=FG=EF,∵DH=CE=BK,∴HG=EK=BC=AD=AB,在△ADH和△ABK中,∴△ADH≌△ABK(SAS),∴AK=AH
(2)∵△ADH≌△ABK,∴∠HAD=∠BAK.∴∠HAK=90°,同理可得:△HGF≌△KEF≌△ABK≌△ADH,∴AH=AK=HF=FK,∴四边形AKFH是正方形
14.如图①,在正方形ABCD中,P是BD上的一点,点E在AD延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
解:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADP=∠CDP,又∵DP=DP,∴△ADP≌△CDP(SAS),∴PA=PC,∵PA=PE,∴PC=PE
(2)∵△ADP≌△CDP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠FCP=∠E,∵∠PFC=∠DFE,∠EDF=90°,∴∠CPE=∠EDF=90°
(3)AP=CE.理由:∵四边形ABCD是菱形,∠ABC=120°,∴∠ADC=120°,∴∠EDF=60°,同(2)可得∠CPE=∠EDF=60°,又∵PC=PE,∴△PCE是等边三角形,∴PE=CE,∵PA=PE,∴AP=CE
一、矩形的性质与判定
【例1】如图,M是矩形ABCD的边AD的中点,P是BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件________________时,四边形PEMF为矩形.
分析:根据已知条件,矩形的性质和判定,欲证明四边形PEMF为矩形,只需证明∠BMC=90°,易得AB=BC时,满足∠BMC=90°的条件.
【对应训练】
1.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A.6 B.8 C.10 D.12
3.【2022·吉林】如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF=_________.
4.【2022·云南改编】如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,则四边形ABCF的面积S为___________.
5.【2023·大庆】如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
二、菱形的性质与判定
【例2】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
分析:(1)易证△FAE≌△CDE,得到AF=CD,再根据D是BC的中点,可得BD=CD,所以AF=BD,从而可证四边形AFBD是平行四边形.(2)利用(1)的结论和点D是BC的中点,可得菱形ADBF的面积=S△ABC,然后根据三角形的面积公式列方程即可求解.
【对应训练】
6.把一个长方形的纸片按如图所示折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是________.
8.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
9.如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连接AF.
(1)求证:FB=AO;
(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.
10.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)对角线AC的长是_________,菱形ABCD的面积是__________;
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系,并说明理由.
三、正方形的性质与判定
【例3】如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.
(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
分析:(1)通过证AB=BC,判断矩形ABCD是正方形;(2)连接AC,先证∠BGP=∠ACB,再根据AC是正方形的对角线即可得出解答.
【对应训练】
11.【2022·重庆】如图,在正方形ABCD中,对角线AC,BD相交于点O.E,F分别为AC,BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( )
A.50° B.55° C.65° D.70°
12.【2023·常德】如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( )
A.80° B.90° C.105° D.115°
13.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.求证:
(1)AK=AH;
(2)四边形AKFH是正方形.
14.如图①,在正方形ABCD中,P是BD上的一点,点E在AD延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、矩形的性质与判定
【例1】如图,M是矩形ABCD的边AD的中点,P是BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件________________时,四边形PEMF为矩形.
分析:根据已知条件,矩形的性质和判定,欲证明四边形PEMF为矩形,只需证明∠BMC=90°,易得AB=BC时,满足∠BMC=90°的条件.
【答案】AB=BC
【对应训练】
1.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( A )
A.4 B.4 C.10 D.8
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( C )
A.6 B.8 C.10 D.12
3.【2022·吉林】如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF=_________.
【答案】
4.【2022·云南改编】如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,则四边形ABCF的面积S为___________.
解:(1)∵四边形ABCD是平行四边形,∴BA∥CD,∴∠BAE=∠FDE,∵点E是AD的中点,∴AE=DE,∵∠BEA=∠FED,△BEA≌△FED(ASA),∴EF=EB,又∵AE=DE,∴四边形ABDF是平行四边形,∵∠BDF=90°,∴四边形ABDF是矩形
(2)18
5.【2023·大庆】如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADE=∠FCE,∠DAE=∠CFE,∵E为线段CD的中点,∴DE=CE,∴△ADE≌△FCE(AAS),∴AE=FE,∴四边形ACFD是平行四边形,∵∠ACF=90°,∴四边形ACFD是
(2)∵四边形ACFD是矩形,∴∠CFD=90°,AC=DF,∵CD=13,CF=5,∴DF===12,∵△ADE≌△FCE,∵△CEF的面积=△ACF的面积=××5×12=15,平行四边形ABCD的面积=BC·AC=5×12=60,∴四边形ABCE的面积=平行四边形ABCD的面积-△ADE的面积=60-15=45
二、菱形的性质与判定
【例2】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
分析:(1)易证△FAE≌△CDE,得到AF=CD,再根据D是BC的中点,可得BD=CD,所以AF=BD,从而可证四边形AFBD是平行四边形.(2)利用(1)的结论和点D是BC的中点,可得菱形ADBF的面积=S△ABC,然后根据三角形的面积公式列方程即可求解.
解:(1)∵AF∥BC,∴∠AFC=∠FCD,∠FAE=∠CDE,∵点E是AD的中点,∴AE=DE,∴△FAE≌△CDE(AAS),∴AF=CD,∵点D是BC的中点,∴BD=CD,∴AF=BD,∴四边形AFBD是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=BD=BC,∴四边形ADBF是菱形
(2)∵四边形ADBF是菱形,∴菱形ADBF的面积=2S△ABD,∵点D是BC的中点,∴△ABC的面积=2S△ABD,∴菱形ADBF的面积=S△ABC=40,∴AB·AC=40,∴×8AC=40,∴AC=10,∴AC的长为10
【对应训练】
6.把一个长方形的纸片按如图所示折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( D )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
7.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是________.
【答案】16
8.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
证明:(1)∵四边形ABCD是菱形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF,在△ABE和△CDF中,∴△ABE≌△CDF(SAS)
(2)如图,连接BD,交AC于O,∵四边形ABCD是菱形,∴BD⊥AC,AO=CO,BO=DO,∵AE=CF,∴EO=FO,∴四边形BEDF是平行四边形,又∵BD⊥EF,∴平行四边形BEDF是菱形
9.如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连接AF.
(1)求证:FB=AO;
(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.
解:(1)∵BF∥AC,∴∠BFE=∠OCE,又∵BE=OE,∠BEF=∠OEC,∴△BEF≌△OEC(AAS),∴BF=OC,又∵OC=AO,∴FB=AO
(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由:∵FB∥AO,且FB=AO,∴四边形AFBO是平行四边形,∵平行四边形ABCD是矩形,∴AC=BD,OA=AC,OB=BD,∴OA=OB,∴四边形AFBO是菱形
10.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)对角线AC的长是_________,菱形ABCD的面积是__________;
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系,并说明理由.
解:(1)12 96
(2)OE+OF的值不变.理由:连接AO,AC,AC交BD于点G,则S△ABD=S△ABO+S△ADO,∴BD·AG=AB·OE+AD·OF,即×16×6=×10OE+×10OF,可得OE+OF=9.6,即OE+OF的值不变
(3)变化,同(2)方法可求得OE-OF=9.6
三、正方形的性质与判定
【例3】如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.
(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
分析:(1)通过证AB=BC,判断矩形ABCD是正方形;(2)连接AC,先证∠BGP=∠ACB,再根据AC是正方形的对角线即可得出解答.
解:(1)四边形ABCD是正方形.证明:∵四边形ABCD是矩形,∴∠ABC=90°,即∠ABP+∠PBC=90°,∵AP⊥BP,∴∠ABP+∠PAB=90°,∴∠PBC=∠PAB,∵CE⊥BP,∴∠APB=∠BEC=90°,又∵BP=CE,∴△ABP≌△BCE(AAS),∴AB=BC,∴矩形ABCD是正方形
(2)连接AC,∵△ABP≌△BCE,∴AP=BE,∵BE=CF,∴AP=CF,∵AP⊥BP,CE⊥BP,∴∠APB=∠CEP=90°,∴AP∥CF,∴四边形ACFP是平行四边形,∴AC∥PF,∴∠ACB=∠BGP,∵四边形ABCD是正方形,AC是对角线,∴∠ACB=45°,∴∠BGP=45°
【对应训练】
11.【2022·重庆】如图,在正方形ABCD中,对角线AC,BD相交于点O.E,F分别为AC,BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( C )
A.50° B.55° C.65° D.70°
12.【2023·常德】如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为( C )
A.80° B.90° C.105° D.115°
13.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.求证:
(1)AK=AH;
(2)四边形AKFH是正方形.
证明:(1)∵四边形ABCD和CEFG都是正方形,∴AB=AD=DC=BC,GC=EC=FG=EF,∵DH=CE=BK,∴HG=EK=BC=AD=AB,在△ADH和△ABK中,∴△ADH≌△ABK(SAS),∴AK=AH
(2)∵△ADH≌△ABK,∴∠HAD=∠BAK.∴∠HAK=90°,同理可得:△HGF≌△KEF≌△ABK≌△ADH,∴AH=AK=HF=FK,∴四边形AKFH是正方形
14.如图①,在正方形ABCD中,P是BD上的一点,点E在AD延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
解:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADP=∠CDP,又∵DP=DP,∴△ADP≌△CDP(SAS),∴PA=PC,∵PA=PE,∴PC=PE
(2)∵△ADP≌△CDP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠FCP=∠E,∵∠PFC=∠DFE,∠EDF=90°,∴∠CPE=∠EDF=90°
(3)AP=CE.理由:∵四边形ABCD是菱形,∠ABC=120°,∴∠ADC=120°,∴∠EDF=60°,同(2)可得∠CPE=∠EDF=60°,又∵PC=PE,∴△PCE是等边三角形,∴PE=CE,∵PA=PE,∴AP=CE
