RJ数学八下专题课堂(四) 利用平行四边形证明线段之间的关系(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(四) 利用平行四边形证明线段之间的关系(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 00:00:00 | ||
图片预览


文档简介
RJ数学八下专题课堂(四) 利用平行四边形证明线段之间的关系
一、证明线段相等
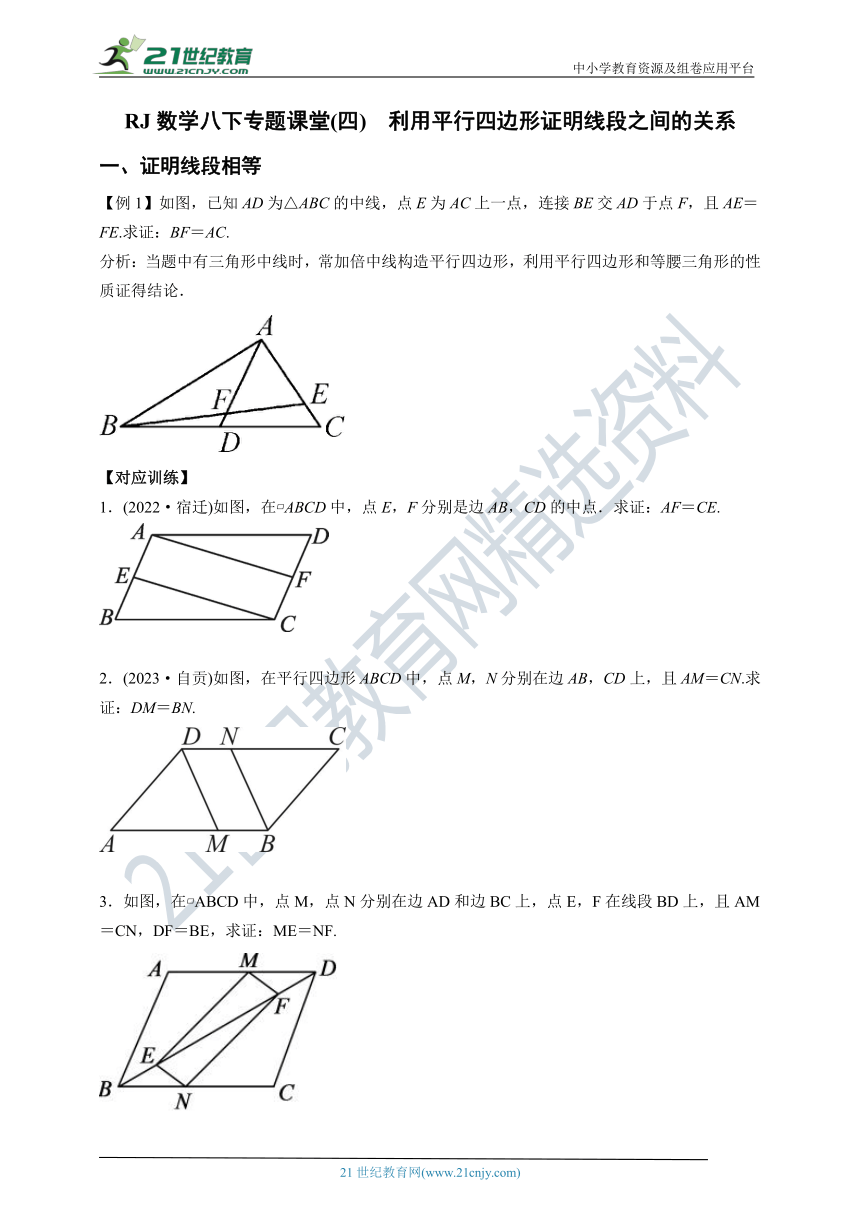
【例1】如图,已知AD为△ABC的中线,点E为AC上一点,连接BE交AD于点F,且AE=FE.求证:BF=AC.
分析:当题中有三角形中线时,常加倍中线构造平行四边形,利用平行四边形和等腰三角形的性质证得结论.
【对应训练】
1.(2022·宿迁)如图,在 ABCD中,点E,F分别是边AB,CD的中点.求证:AF=CE.
2.(2023·自贡)如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
3.如图,在 ABCD中,点M,点N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE,求证:ME=NF.
二、证明线段平行
【例2】如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E,F,求证:BE∥DF.
分析:证四边形BEDF为平行四边形即可.
【对应训练】
4.如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由.
5.已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
三、证明线段互相平分
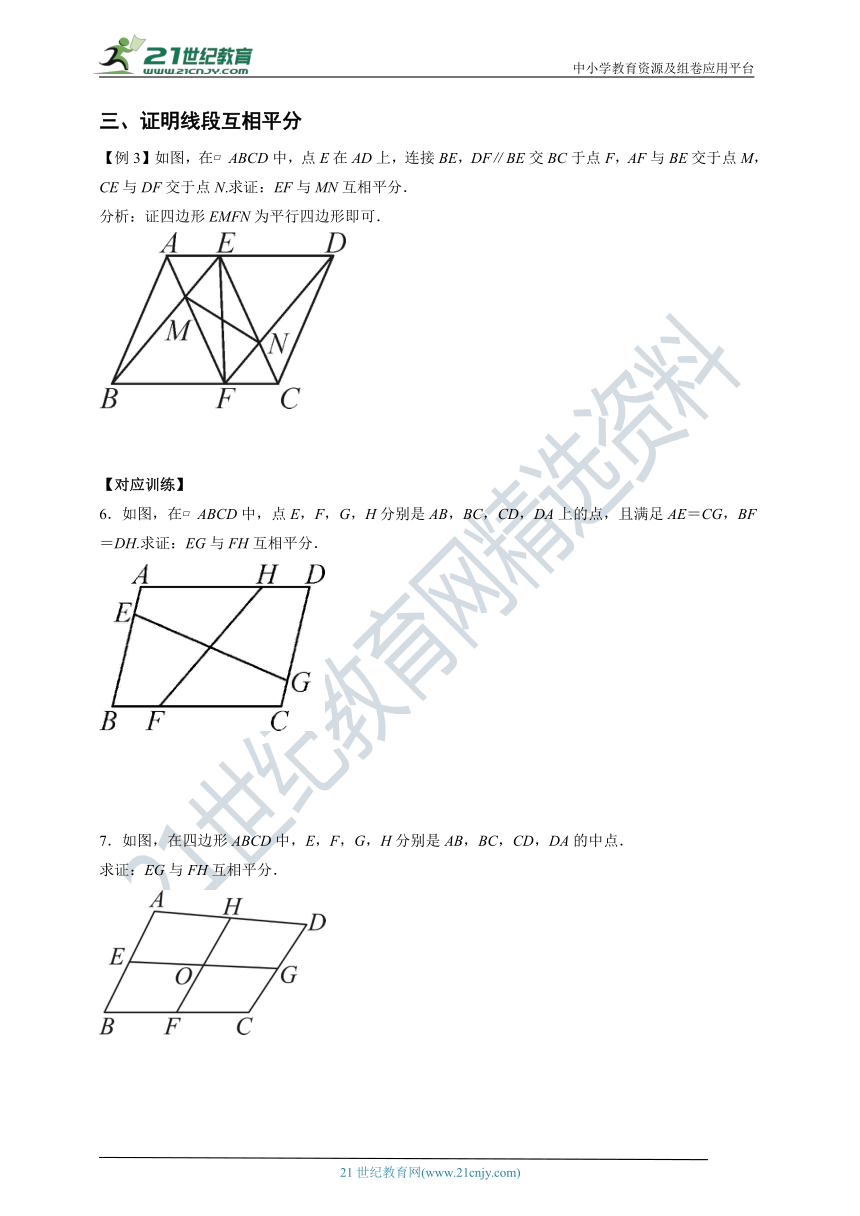
【例3】如图,在 ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
分析:证四边形EMFN为平行四边形即可.
【对应训练】
6.如图,在 ABCD中,点E,F,G,H分别是AB,BC,CD,DA上的点,且满足AE=CG,BF=DH.求证:EG与FH互相平分.
7.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:EG与FH互相平分.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、证明线段相等
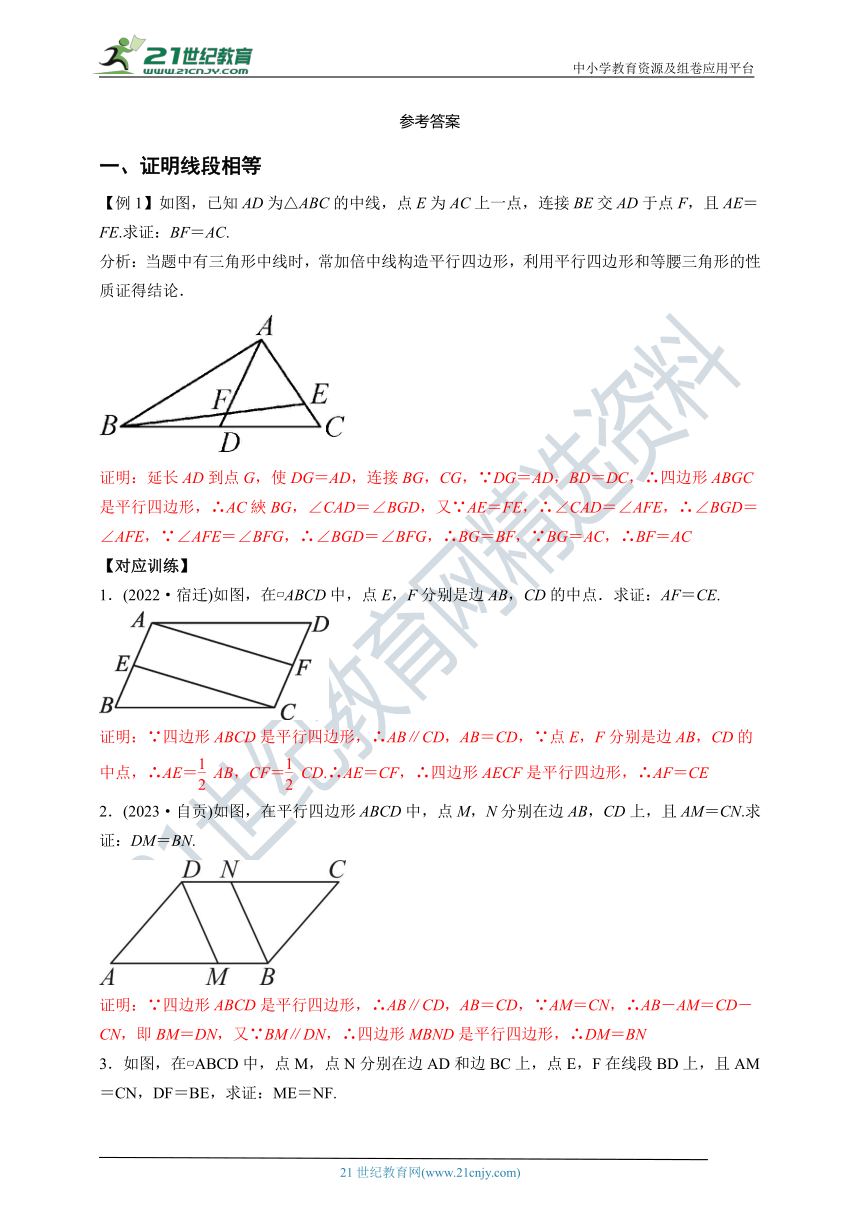
【例1】如图,已知AD为△ABC的中线,点E为AC上一点,连接BE交AD于点F,且AE=FE.求证:BF=AC.
分析:当题中有三角形中线时,常加倍中线构造平行四边形,利用平行四边形和等腰三角形的性质证得结论.
证明:延长AD到点G,使DG=AD,连接BG,CG,∵DG=AD,BD=DC,∴四边形ABGC是平行四边形,∴AC綊BG,∠CAD=∠BGD,又∵AE=FE,∴∠CAD=∠AFE,∴∠BGD=∠AFE,∵∠AFE=∠BFG,∴∠BGD=∠BFG,∴BG=BF,∵BG=AC,∴BF=AC
【对应训练】
1.(2022·宿迁)如图,在 ABCD中,点E,F分别是边AB,CD的中点.求证:AF=CE.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵点E,F分别是边AB,CD的中点,∴AE=AB,CF=CD.∴AE=CF,∴四边形AECF是平行四边形,∴AF=CE
2.(2023·自贡)如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵AM=CN,∴AB-AM=CD-CN,即BM=DN,又∵BM∥DN,∴四边形MBND是平行四边形,∴DM=BN
3.如图,在 ABCD中,点M,点N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE,求证:ME=NF.
证明:先证△DMF≌△BNE,得EN=MF,又可证EN∥MF,∴四边形MFNE是平行四边形,∴ME=NF.
二、证明线段平行
【例2】如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E,F,求证:BE∥DF.
分析:证四边形BEDF为平行四边形即可.
证明:∵四边形ABCD是平行四边形,∴AD綊BC,∴∠DAE=∠BCF,∵DE⊥AC,BF⊥AC,∴DE∥BF,∴∠DEF=∠BFE=90°,∴∠DEA=∠BFC=90°,∴△ADE≌△CBF(AAS).∴DE=BF,∴四边形BEDF为平行四边形,∴BE∥DF
【对应训练】
4.如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由.
解:AECF.先证△AOF≌△COE,从而得到OE=OF,再证四边形AECF是平行四边形,从而可得AECF.
5.已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
证明:(1)∵AE=CF,∴AE+EF=CF+EF,即AF=CE.又四边形ABCD是平行四边形,∴AD=CB,AD∥CB.∴∠DAF=∠BCE.∴△ADF≌△CBE(SAS)
(2)∵△ADF≌△CBE,∴∠DFA=∠BEC.∴EB∥DF
三、证明线段互相平分
【例3】如图,在 ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
分析:证四边形EMFN为平行四边形即可.
证明:先证四边形BEDF是平行四边形,得AE=CF,再证四边形AFCE是平行四边形,从而可得AF∥CE,再证四边形EMFN是平行四边形,即可证得EF与MN互相平分
【对应训练】
6.如图,在 ABCD中,点E,F,G,H分别是AB,BC,CD,DA上的点,且满足AE=CG,BF=DH.求证:EG与FH互相平分.
证明:连接EH,EF,FG,GH,易证△AEH≌△CGF,∴EH=GF,同理EF=HG,∴四边形EFGH为平行四边形,∴EG与FH互相平分
7.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:EG与FH互相平分.
分析:连接EF,FG,GH,HE,AC,证四边形EFGH是平行四边形即可.
证明:连接EF,FG,GH,HE,AC,∵E,F,G,H分别是AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△ACD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形,∴EG与FH互相平分
一、证明线段相等
【例1】如图,已知AD为△ABC的中线,点E为AC上一点,连接BE交AD于点F,且AE=FE.求证:BF=AC.
分析:当题中有三角形中线时,常加倍中线构造平行四边形,利用平行四边形和等腰三角形的性质证得结论.
【对应训练】
1.(2022·宿迁)如图,在 ABCD中,点E,F分别是边AB,CD的中点.求证:AF=CE.
2.(2023·自贡)如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
3.如图,在 ABCD中,点M,点N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE,求证:ME=NF.
二、证明线段平行
【例2】如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E,F,求证:BE∥DF.
分析:证四边形BEDF为平行四边形即可.
【对应训练】
4.如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由.
5.已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
三、证明线段互相平分
【例3】如图,在 ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
分析:证四边形EMFN为平行四边形即可.
【对应训练】
6.如图,在 ABCD中,点E,F,G,H分别是AB,BC,CD,DA上的点,且满足AE=CG,BF=DH.求证:EG与FH互相平分.
7.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:EG与FH互相平分.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、证明线段相等
【例1】如图,已知AD为△ABC的中线,点E为AC上一点,连接BE交AD于点F,且AE=FE.求证:BF=AC.
分析:当题中有三角形中线时,常加倍中线构造平行四边形,利用平行四边形和等腰三角形的性质证得结论.
证明:延长AD到点G,使DG=AD,连接BG,CG,∵DG=AD,BD=DC,∴四边形ABGC是平行四边形,∴AC綊BG,∠CAD=∠BGD,又∵AE=FE,∴∠CAD=∠AFE,∴∠BGD=∠AFE,∵∠AFE=∠BFG,∴∠BGD=∠BFG,∴BG=BF,∵BG=AC,∴BF=AC
【对应训练】
1.(2022·宿迁)如图,在 ABCD中,点E,F分别是边AB,CD的中点.求证:AF=CE.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵点E,F分别是边AB,CD的中点,∴AE=AB,CF=CD.∴AE=CF,∴四边形AECF是平行四边形,∴AF=CE
2.(2023·自贡)如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵AM=CN,∴AB-AM=CD-CN,即BM=DN,又∵BM∥DN,∴四边形MBND是平行四边形,∴DM=BN
3.如图,在 ABCD中,点M,点N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE,求证:ME=NF.
证明:先证△DMF≌△BNE,得EN=MF,又可证EN∥MF,∴四边形MFNE是平行四边形,∴ME=NF.
二、证明线段平行
【例2】如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E,F,求证:BE∥DF.
分析:证四边形BEDF为平行四边形即可.
证明:∵四边形ABCD是平行四边形,∴AD綊BC,∴∠DAE=∠BCF,∵DE⊥AC,BF⊥AC,∴DE∥BF,∴∠DEF=∠BFE=90°,∴∠DEA=∠BFC=90°,∴△ADE≌△CBF(AAS).∴DE=BF,∴四边形BEDF为平行四边形,∴BE∥DF
【对应训练】
4.如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由.
解:AECF.先证△AOF≌△COE,从而得到OE=OF,再证四边形AECF是平行四边形,从而可得AECF.
5.已知:如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
证明:(1)∵AE=CF,∴AE+EF=CF+EF,即AF=CE.又四边形ABCD是平行四边形,∴AD=CB,AD∥CB.∴∠DAF=∠BCE.∴△ADF≌△CBE(SAS)
(2)∵△ADF≌△CBE,∴∠DFA=∠BEC.∴EB∥DF
三、证明线段互相平分
【例3】如图,在 ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
分析:证四边形EMFN为平行四边形即可.
证明:先证四边形BEDF是平行四边形,得AE=CF,再证四边形AFCE是平行四边形,从而可得AF∥CE,再证四边形EMFN是平行四边形,即可证得EF与MN互相平分
【对应训练】
6.如图,在 ABCD中,点E,F,G,H分别是AB,BC,CD,DA上的点,且满足AE=CG,BF=DH.求证:EG与FH互相平分.
证明:连接EH,EF,FG,GH,易证△AEH≌△CGF,∴EH=GF,同理EF=HG,∴四边形EFGH为平行四边形,∴EG与FH互相平分
7.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:EG与FH互相平分.
分析:连接EF,FG,GH,HE,AC,证四边形EFGH是平行四边形即可.
证明:连接EF,FG,GH,HE,AC,∵E,F,G,H分别是AB,BC,CD,DA的中点,∴EF是△ABC的中位线,GH是△ACD的中位线,∴EF∥AC,EF=AC,GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形,∴EG与FH互相平分
