RJ数学八下专题课堂(十) 正方形中常见的几何图形结构(含答案)
文档属性
| 名称 | RJ数学八下专题课堂(十) 正方形中常见的几何图形结构(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 10:35:16 | ||
图片预览



文档简介
RJ数学八下专题课堂(十)正方形中常见的几何图形结构
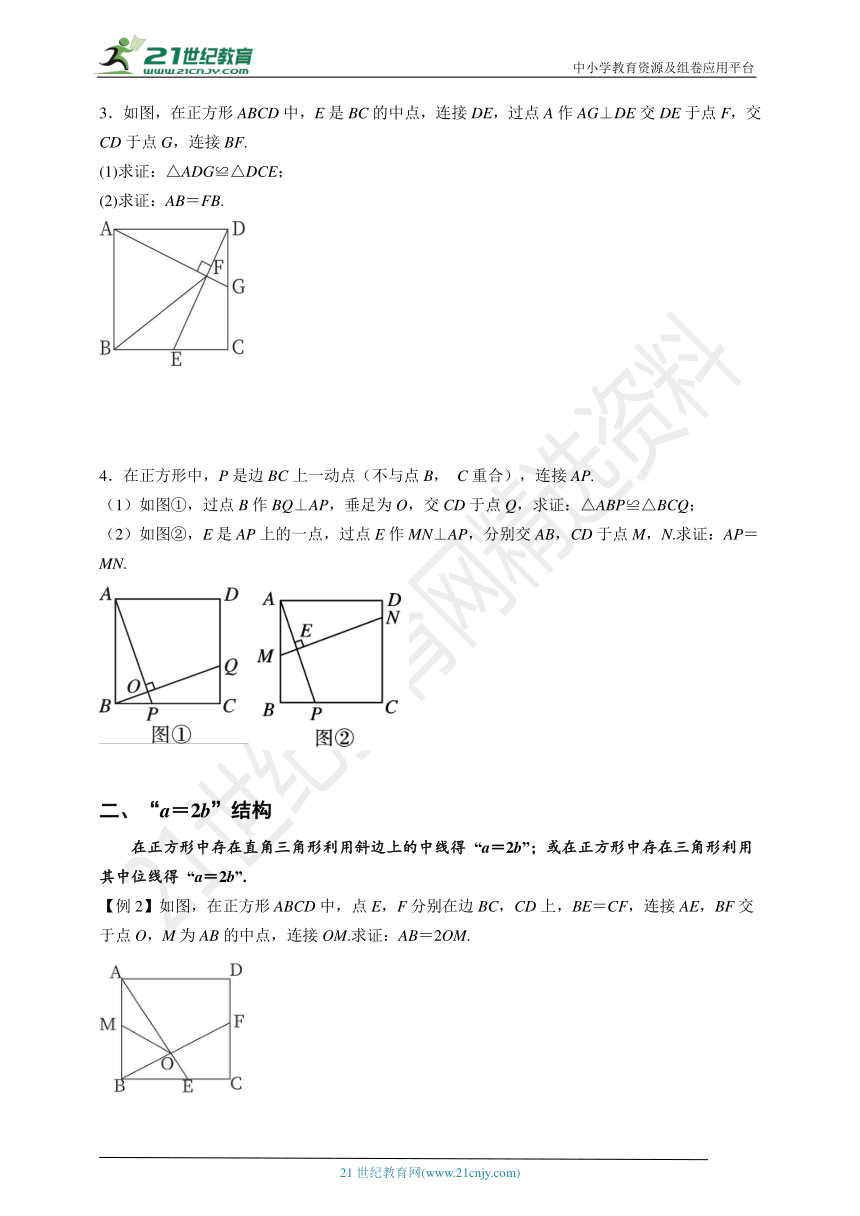
一、“十字架”结构
正方形中存在端点在正方形的边上且互相垂直的线段,看起来像“十字架”,利用垂直证明三角形全等得出线段或角的关系.
【例1】如图,在正方形ABCD中,AE平分∠BAC交BC于点E,F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A.45° B.60° C.67.5° D.77.5°
【对应训练】
1.(1)如图1,在正方形ABCD中,若CE⊥DF,则线段CE与DF有何数量关系?请说明理由.
(2)如图2,在正方形ABCD中,若GE⊥HF,则线GE与HF有何数量关系?请说明理由.
图1 图2
2.如图,在正方形ABCD中,点E,F分别在BC,CD边上,AE⊥BF于点G,CH⊥BF于点H,BG=HG.
(1)求证:BH=AG;
(2)若AB=4,求CH的长.
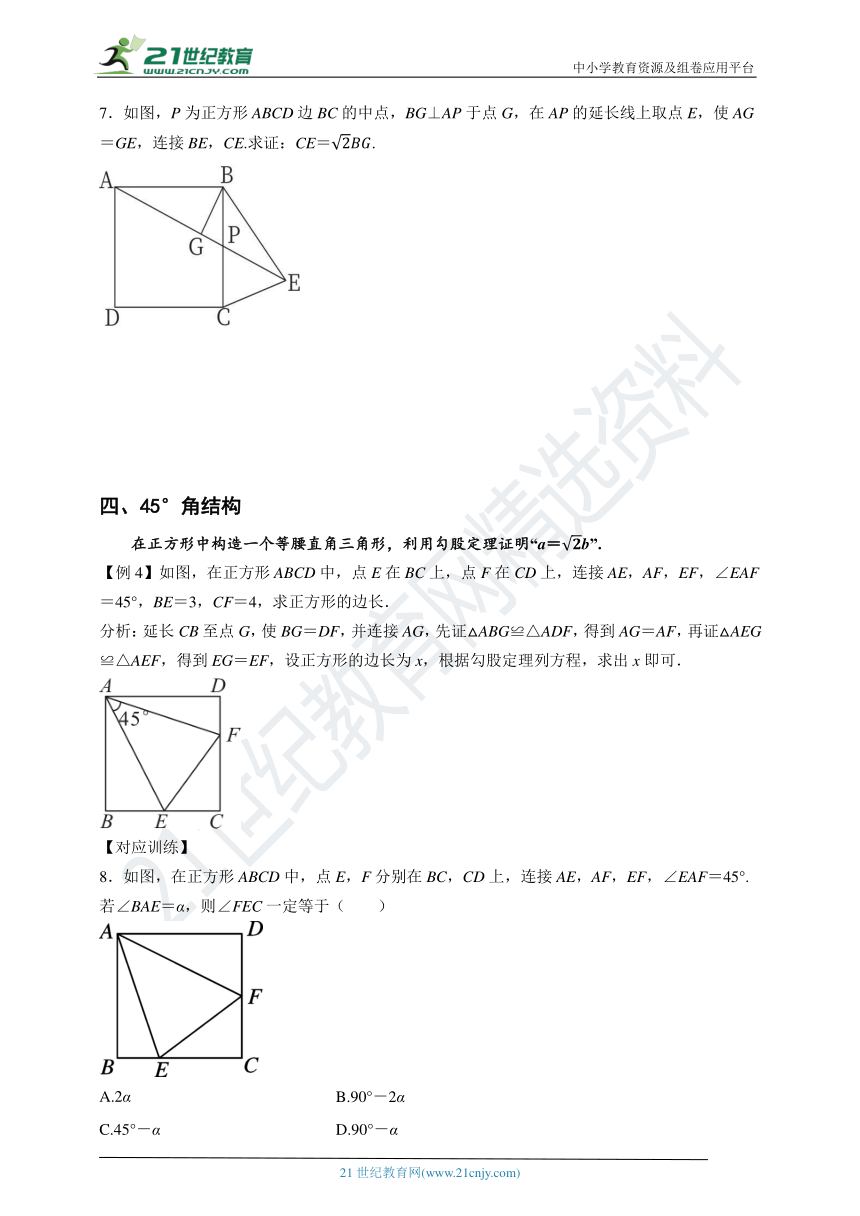
3.如图,在正方形ABCD中,E是BC的中点,连接DE,过点A作AG⊥DE交DE于点F,交CD于点G,连接BF.
(1)求证:△ADG≌△DCE;
(2)求证:AB=FB.
4.在正方形中,P是边BC上一动点(不与点B, C重合),连接AP.
(1)如图①,过点B作BQ⊥AP,垂足为O,交CD于点Q,求证:△ABP≌△BCQ;
(2)如图②,E是AP上的一点,过点E作MN⊥AP,分别交AB,CD于点M,N.求证:AP=MN.
二、“a=2b”结构
在正方形中存在直角三角形利用斜边上的中线得 “a=2b”;或在正方形中存在三角形利用其中位线得 “a=2b”.
【例2】如图,在正方形ABCD中,点E,F分别在边BC,CD上,BE=CF,连接AE,BF交于点O,M为AB的中点,连接OM.求证:AB=2OM.
【对应训练】
5.如图,在正方形ABCD中,O为对角线的交点,AE平分∠BAC交BC于点E,交OB于点F.求证:CE=2OF.
三、“a=”结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例3】如图,在正方形ABCD中,AC,BD交于点O,E为OD上一点,且BE=BA,连接AE.
(1)求证:AE平分∠DAC;
(2)求证:DE=.
【对应训练】
6.如图,在正方形ABCD中,E为AC上一点,F为CD上一点,且ED=EF.求证:BF=.
7.如图,P为正方形ABCD边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE,CE.求证:CE=.
四、45°角结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例4】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,求正方形的边长.
分析:延长CB至点G,使BG=DF,并连接AG,先证△ABG≌△ADF,得到AG=AF,再证△AEG≌△AEF,得到EG=EF,设正方形的边长为x,根据勾股定理列方程,求出x即可.
【对应训练】
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( )
A.2α B.90°-2α
C.45°-α D.90°-α
9.如图,正方形ABCD中,E是AD上一点,F是AB延长线上一点,DE=BF.点G,H分别在边AB,CD上,且GH=3,GH交EF于M.若∠EMH=45°,求EF的长.
10.如图,在正方形ABCD中,点E为BC的中点,F为AB上一点,AE,CF交于点O.若AB=6,∠AOF=45°,求BF的长.
11.如图,在正方形ABCD中,E,F分别为边BC,CD上两点,∠EAF=45°.
(1)若EA是∠BEF的平分线,求证:FA是∠DFE的平分线;
(2)若BE=DF,求证:EF=BE+DF.
五、手拉手结构
【例5】如图,G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)若AB=3,AG=3,求EB的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、“十字架”结构
正方形中存在端点在正方形的边上且互相垂直的线段,看起来像“十字架”,利用垂直证明三角形全等得出线段或角的关系.
【例1】如图,在正方形ABCD中,AE平分∠BAC交BC于点E,F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( C )
A.45° B.60° C.67.5° D.77.5°
【对应训练】
1.(1)如图1,在正方形ABCD中,若CE⊥DF,则线段CE与DF有何数量关系?请说明理由.
(2)如图2,在正方形ABCD中,若GE⊥HF,则线GE与HF有何数量关系?请说明理由.
图1 图2
解:(1)CE=DF.理由略.
(2)GE=HF.理由略.
2.如图,在正方形ABCD中,点E,F分别在BC,CD边上,AE⊥BF于点G,CH⊥BF于点H,BG=HG.
(1)求证:BH=AG;
(2)若AB=4,求CH的长.
解:(1)易证△ABG≌△BCH,∴BH=AG.
(2)由(1)知△ABG≌△BCH,
∴CH=BG=HG.
设CH=BG=x,则AG=2x.
在Rt△ABG中,x2+(2x)2=42,
∴x=(负值舍去),即CH=.
3.如图,在正方形ABCD中,E是BC的中点,连接DE,过点A作AG⊥DE交DE于点F,交CD于点G,连接BF.
(1)求证:△ADG≌△DCE;
(2)求证:AB=FB.
证明:(1)证明略.
(2)延长DE交AB延长线于点H.
∵E是BC的中点,∴BE=CE.
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE,
∴BH=DC=AB,即B是AH的中点.
又∵∠AFH=90°,∴FB==AB.
4.在正方形中,P是边BC上一动点(不与点B, C重合),连接AP.
(1)如图①,过点B作BQ⊥AP,垂足为O,交CD于点Q,求证:△ABP≌△BCQ;
(2)如图②,E是AP上的一点,过点E作MN⊥AP,分别交AB,CD于点M,N.求证:AP=MN.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°.
∴∠PAB=∠CBQ.
在△ABP和△BCQ中,
∴△ABP≌△BCQ(ASA).
证明:(2)过点M作MG⊥CD于点G,
则四边形AMGD是矩形,
∴MG=AD,∠MGN=90°.
∵四边形ABCD是正方形,
∴∠ABP=90°,AB=BC=AD.
∴MG=AB,∠ABP=∠MGN.
又∵MN⊥AP,∴∠AEM=90°.
∴∠AME+∠BAP=90°.
又∵∠NMG+∠AME=90°,
∴∠NMG=∠BAP.
∴△ABP≌△MGN(ASA).
∴AP=MN.
二、“a=2b”结构
在正方形中存在直角三角形利用斜边上的中线得 “a=2b”;或在正方形中存在三角形利用其中位线得 “a=2b”.
【例2】如图,在正方形ABCD中,点E,F分别在边BC,CD上,BE=CF,连接AE,BF交于点O,M为AB的中点,连接OM.求证:AB=2OM.
证明:易证△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABO+∠CBF=90°,
∴∠ABO+∠BAO=90°,即∠AOB=90°.
在Rt△ABO中,M是斜边AB的中点,
∴OM=,即AB=2OM.
【对应训练】
5.如图,在正方形ABCD中,O为对角线的交点,AE平分∠BAC交BC于点E,交OB于点F.求证:CE=2OF.
解:取AE的中点M,连接OM.
易知OA=OC,MA=ME,∠OFM=67.5°,
∴OM=,OM∥CE,
∴∠MOA=∠BCA=45°,
∴∠OMF=∠EAC+∠MOA=67.5°,
∴∠OFM=∠OMF,∴OF=OM=,
∴CE=2OF.
三、“a=”结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例3】如图,在正方形ABCD中,AC,BD交于点O,E为OD上一点,且BE=BA,连接AE.
(1)求证:AE平分∠DAC;
(2)求证:DE=.
证明:(1)∵∠ABE=45°,BE=BA,
∴∠BAE=∠BEA=67.5°.
∵∠BAC=∠DAC=45°,
∴∠DAE=∠OAE=22.5°,
∴AE平分∠DAC.
(2)过点E作EM⊥AD于点M.
∵AE平分∠DAC,EO⊥AO,EM⊥AD,
∴OE=EM,∴DE=.
【对应训练】
6.如图,在正方形ABCD中,E为AC上一点,F为CD上一点,且ED=EF.求证:BF=.
证明:连接BE.易证△CBE≌△CDE,
∴EB=ED=EF,∠EBC=∠EDC=∠EFD.
∵∠EFD+∠EFC=180°,
∴∠EBC+∠EFC=180°,
∴∠BEF+∠BCD=180°.
∵∠BCD=90°,∴∠BEF=90°,
∴BF=.
7.如图,P为正方形ABCD边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE,CE.求证:CE=.
证明:过点C作CH⊥AE于点H.
∵BG⊥AE,CH⊥AE,
∴∠BGP=∠CHP=∠CHE=90°.
∵P为BC的中点,∴BP=CP.
易证△BGP≌△CHP,
∴BG=CH,∠PBG=∠PCH.
易知AB=BE,∴∠BAE=∠BEA.
∵∠ABC=∠ABG+∠PBG=90°,∠ABG+∠BAG=90°,
∴∠PBG=∠BAG,∴∠PCH=∠BEA.
∵AB=BC,∴BC=BE,∴∠BCE=∠BEC,
∴∠HCE=∠HEC,∴CH=EH.
∵∠CHE=90°,∴CE=.
四、45°角结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例4】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,求正方形的边长.
分析:延长CB至点G,使BG=DF,并连接AG,先证△ABG≌△ADF,得到AG=AF,再证△AEG≌△AEF,得到EG=EF,设正方形的边长为x,根据勾股定理列方程,求出x即可.
解:延长CB至点G,使BG=DF,并连接AG,在△ABG和△ADF中, ∴△ABG≌△ADF(SAS),∴AG=AF,∠GAB=∠DAF,∵∠EAF=45°,∴∠BAE+∠DAF=∠BAE+∠GAB=∠GAE=45°,∴∠EAF=∠GAE.在△AEG和△AEF中,∴△AEG≌△AEF(SAS).∴GE=EF,
设正方形的边长为x,DF=x-4,EC=x-3,GE=EF=BG+BE=DF+BE=x-4+3=x-1,
在Rt△EFC中,EF2=EC2+CF2,即(x-1)2=(x-3)2+42,解得x=6,即正方形的边长为6
【对应训练】
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( A )
A.2α B.90°-2α
C.45°-α D.90°-α
9.如图,正方形ABCD中,E是AD上一点,F是AB延长线上一点,DE=BF.点G,H分别在边AB,CD上,且GH=3,GH交EF于M.若∠EMH=45°,求EF的长.
解:连接CE,CF,如图,∵四边形ABCD是正方形,∴AB∥DC,BC=DC,∠ABC=∠D=90°,∴∠FBC=90°=∠D,在△FBC和△EDC中, ∴△FBC≌△EDC (SAS),∴CF=CE,∠FCB=∠ECD,∴∠ECF=∠ECB+∠FCB=∠ECB+∠ECD=90°,∴△CEF是等腰直角三角形,
∴∠EFC=45°,EF=CF,∵∠EMH=45°,
∴∠EFC=∠EMH,∴GH∥FC,∵AF∥DC,
∴四边形FCHG是平行四边形,∴CF=GH=3,
∴EF=CF=3
10.如图,在正方形ABCD中,点E为BC的中点,F为AB上一点,AE,CF交于点O.若AB=6,∠AOF=45°,求BF的长.
解:过点C作CM∥AE交AD于点M,延长AD到点N,使得DN=BF,连接CN,FM,如图所示,在正方形ABCD中,AD∥BC,AD=BC=CD,∠BAD=∠B=∠ADC=90°,∴∠NDC=∠B=90°,∴△NDC≌△FBC(SAS),∴CF=CN,∠DCN=∠BCF,
∵∠AOF=45°,CM∥AE,∴∠MCF=∠AOF=45°,∴∠MCN=∠MCD+∠DCN=45°,∴∠MCF=∠MCN,
在△MCF和△MCN中, ∴△MCF≌△MCN (SAS),∴MF=MN,∵AD∥BC,AE∥MC,∴四边形AECM是平行四边形,∴CE=AM,∵E是BC的中点,∴M是AD的中点,∵AB=6,∴AD=AB=6,∴AM=DM=3,设BF=x,则DN=x,AF=6-x,∴MF=MN=3+x,在Rt△AFM中,根据勾股定理,得32+(6-x)2=(3+x)2,解得x=2,∴BF=2
11.如图,在正方形ABCD中,E,F分别为边BC,CD上两点,∠EAF=45°.
(1)若EA是∠BEF的平分线,求证:FA是∠DFE的平分线;
(2)若BE=DF,求证:EF=BE+DF.
证明:(1)过点A作AH⊥EF于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°.
∵∠AHE=90°,∴∠B=∠AHE.
∵EA是∠BEF的平分线,
∴∠AEB=∠AEH.
在△ABE与△AHE中,
∴△ABE≌△AHE(AAS).∴AB=AH.
∵AB=AD,∴AH=AD.
在Rt△AHF与Rt△ADF中,
∴Rt△AHF≌Rt△ADF(HL).∴∠AFE=∠AFD.
∴FA是∠DFE的平分线.
证明:(2)如图,过点A作∠GAB=∠FAD,且G为CB边延长线上一点.
∵四边形ABCD为正方形,
∴∠D=∠ABC=90°,AB=AD.
∴∠ABG=90°.∴∠ABG=∠D.
在△GAB和△FAD中,
∴△GAB≌△FAD(ASA).∴BG=DF,AG=AF.
∵∠DAF+∠BAF=90°,∠GAB=∠FAD,
∴∠GAB+∠FAB=90°.∴∠GAF=90°.
∵∠EAF=45°,∴∠GAE=∠FAE=45°.
在△GAE和△FAE中,
∴△GAE≌△FAE(SAS).∴GE=EF.
∵GE=BG+BE,∴DF+BE=EF.
五、手拉手结构
【例5】如图,G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)若AB=3,AG=3,求EB的长.
解:(1)证明:∵四边形ABCD,
AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG.
∴∠EAB=∠GAD.
在△AEB和△AGD中,
∴△EAB≌△GAD(SAS).
解:(2)∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD==6.
∴∠DOG=90°,OA=OD=BD=3.
∵AG=3,∴OG=OA+AG=6.
∴GD===3.
∴EB=3.
一、“十字架”结构
正方形中存在端点在正方形的边上且互相垂直的线段,看起来像“十字架”,利用垂直证明三角形全等得出线段或角的关系.
【例1】如图,在正方形ABCD中,AE平分∠BAC交BC于点E,F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A.45° B.60° C.67.5° D.77.5°
【对应训练】
1.(1)如图1,在正方形ABCD中,若CE⊥DF,则线段CE与DF有何数量关系?请说明理由.
(2)如图2,在正方形ABCD中,若GE⊥HF,则线GE与HF有何数量关系?请说明理由.
图1 图2
2.如图,在正方形ABCD中,点E,F分别在BC,CD边上,AE⊥BF于点G,CH⊥BF于点H,BG=HG.
(1)求证:BH=AG;
(2)若AB=4,求CH的长.
3.如图,在正方形ABCD中,E是BC的中点,连接DE,过点A作AG⊥DE交DE于点F,交CD于点G,连接BF.
(1)求证:△ADG≌△DCE;
(2)求证:AB=FB.
4.在正方形中,P是边BC上一动点(不与点B, C重合),连接AP.
(1)如图①,过点B作BQ⊥AP,垂足为O,交CD于点Q,求证:△ABP≌△BCQ;
(2)如图②,E是AP上的一点,过点E作MN⊥AP,分别交AB,CD于点M,N.求证:AP=MN.
二、“a=2b”结构
在正方形中存在直角三角形利用斜边上的中线得 “a=2b”;或在正方形中存在三角形利用其中位线得 “a=2b”.
【例2】如图,在正方形ABCD中,点E,F分别在边BC,CD上,BE=CF,连接AE,BF交于点O,M为AB的中点,连接OM.求证:AB=2OM.
【对应训练】
5.如图,在正方形ABCD中,O为对角线的交点,AE平分∠BAC交BC于点E,交OB于点F.求证:CE=2OF.
三、“a=”结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例3】如图,在正方形ABCD中,AC,BD交于点O,E为OD上一点,且BE=BA,连接AE.
(1)求证:AE平分∠DAC;
(2)求证:DE=.
【对应训练】
6.如图,在正方形ABCD中,E为AC上一点,F为CD上一点,且ED=EF.求证:BF=.
7.如图,P为正方形ABCD边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE,CE.求证:CE=.
四、45°角结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例4】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,求正方形的边长.
分析:延长CB至点G,使BG=DF,并连接AG,先证△ABG≌△ADF,得到AG=AF,再证△AEG≌△AEF,得到EG=EF,设正方形的边长为x,根据勾股定理列方程,求出x即可.
【对应训练】
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( )
A.2α B.90°-2α
C.45°-α D.90°-α
9.如图,正方形ABCD中,E是AD上一点,F是AB延长线上一点,DE=BF.点G,H分别在边AB,CD上,且GH=3,GH交EF于M.若∠EMH=45°,求EF的长.
10.如图,在正方形ABCD中,点E为BC的中点,F为AB上一点,AE,CF交于点O.若AB=6,∠AOF=45°,求BF的长.
11.如图,在正方形ABCD中,E,F分别为边BC,CD上两点,∠EAF=45°.
(1)若EA是∠BEF的平分线,求证:FA是∠DFE的平分线;
(2)若BE=DF,求证:EF=BE+DF.
五、手拉手结构
【例5】如图,G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)若AB=3,AG=3,求EB的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、“十字架”结构
正方形中存在端点在正方形的边上且互相垂直的线段,看起来像“十字架”,利用垂直证明三角形全等得出线段或角的关系.
【例1】如图,在正方形ABCD中,AE平分∠BAC交BC于点E,F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( C )
A.45° B.60° C.67.5° D.77.5°
【对应训练】
1.(1)如图1,在正方形ABCD中,若CE⊥DF,则线段CE与DF有何数量关系?请说明理由.
(2)如图2,在正方形ABCD中,若GE⊥HF,则线GE与HF有何数量关系?请说明理由.
图1 图2
解:(1)CE=DF.理由略.
(2)GE=HF.理由略.
2.如图,在正方形ABCD中,点E,F分别在BC,CD边上,AE⊥BF于点G,CH⊥BF于点H,BG=HG.
(1)求证:BH=AG;
(2)若AB=4,求CH的长.
解:(1)易证△ABG≌△BCH,∴BH=AG.
(2)由(1)知△ABG≌△BCH,
∴CH=BG=HG.
设CH=BG=x,则AG=2x.
在Rt△ABG中,x2+(2x)2=42,
∴x=(负值舍去),即CH=.
3.如图,在正方形ABCD中,E是BC的中点,连接DE,过点A作AG⊥DE交DE于点F,交CD于点G,连接BF.
(1)求证:△ADG≌△DCE;
(2)求证:AB=FB.
证明:(1)证明略.
(2)延长DE交AB延长线于点H.
∵E是BC的中点,∴BE=CE.
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE,
∴BH=DC=AB,即B是AH的中点.
又∵∠AFH=90°,∴FB==AB.
4.在正方形中,P是边BC上一动点(不与点B, C重合),连接AP.
(1)如图①,过点B作BQ⊥AP,垂足为O,交CD于点Q,求证:△ABP≌△BCQ;
(2)如图②,E是AP上的一点,过点E作MN⊥AP,分别交AB,CD于点M,N.求证:AP=MN.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°.
∴∠PAB=∠CBQ.
在△ABP和△BCQ中,
∴△ABP≌△BCQ(ASA).
证明:(2)过点M作MG⊥CD于点G,
则四边形AMGD是矩形,
∴MG=AD,∠MGN=90°.
∵四边形ABCD是正方形,
∴∠ABP=90°,AB=BC=AD.
∴MG=AB,∠ABP=∠MGN.
又∵MN⊥AP,∴∠AEM=90°.
∴∠AME+∠BAP=90°.
又∵∠NMG+∠AME=90°,
∴∠NMG=∠BAP.
∴△ABP≌△MGN(ASA).
∴AP=MN.
二、“a=2b”结构
在正方形中存在直角三角形利用斜边上的中线得 “a=2b”;或在正方形中存在三角形利用其中位线得 “a=2b”.
【例2】如图,在正方形ABCD中,点E,F分别在边BC,CD上,BE=CF,连接AE,BF交于点O,M为AB的中点,连接OM.求证:AB=2OM.
证明:易证△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABO+∠CBF=90°,
∴∠ABO+∠BAO=90°,即∠AOB=90°.
在Rt△ABO中,M是斜边AB的中点,
∴OM=,即AB=2OM.
【对应训练】
5.如图,在正方形ABCD中,O为对角线的交点,AE平分∠BAC交BC于点E,交OB于点F.求证:CE=2OF.
解:取AE的中点M,连接OM.
易知OA=OC,MA=ME,∠OFM=67.5°,
∴OM=,OM∥CE,
∴∠MOA=∠BCA=45°,
∴∠OMF=∠EAC+∠MOA=67.5°,
∴∠OFM=∠OMF,∴OF=OM=,
∴CE=2OF.
三、“a=”结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例3】如图,在正方形ABCD中,AC,BD交于点O,E为OD上一点,且BE=BA,连接AE.
(1)求证:AE平分∠DAC;
(2)求证:DE=.
证明:(1)∵∠ABE=45°,BE=BA,
∴∠BAE=∠BEA=67.5°.
∵∠BAC=∠DAC=45°,
∴∠DAE=∠OAE=22.5°,
∴AE平分∠DAC.
(2)过点E作EM⊥AD于点M.
∵AE平分∠DAC,EO⊥AO,EM⊥AD,
∴OE=EM,∴DE=.
【对应训练】
6.如图,在正方形ABCD中,E为AC上一点,F为CD上一点,且ED=EF.求证:BF=.
证明:连接BE.易证△CBE≌△CDE,
∴EB=ED=EF,∠EBC=∠EDC=∠EFD.
∵∠EFD+∠EFC=180°,
∴∠EBC+∠EFC=180°,
∴∠BEF+∠BCD=180°.
∵∠BCD=90°,∴∠BEF=90°,
∴BF=.
7.如图,P为正方形ABCD边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE,CE.求证:CE=.
证明:过点C作CH⊥AE于点H.
∵BG⊥AE,CH⊥AE,
∴∠BGP=∠CHP=∠CHE=90°.
∵P为BC的中点,∴BP=CP.
易证△BGP≌△CHP,
∴BG=CH,∠PBG=∠PCH.
易知AB=BE,∴∠BAE=∠BEA.
∵∠ABC=∠ABG+∠PBG=90°,∠ABG+∠BAG=90°,
∴∠PBG=∠BAG,∴∠PCH=∠BEA.
∵AB=BC,∴BC=BE,∴∠BCE=∠BEC,
∴∠HCE=∠HEC,∴CH=EH.
∵∠CHE=90°,∴CE=.
四、45°角结构
在正方形中构造一个等腰直角三角形,利用勾股定理证明“a=b”.
【例4】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,求正方形的边长.
分析:延长CB至点G,使BG=DF,并连接AG,先证△ABG≌△ADF,得到AG=AF,再证△AEG≌△AEF,得到EG=EF,设正方形的边长为x,根据勾股定理列方程,求出x即可.
解:延长CB至点G,使BG=DF,并连接AG,在△ABG和△ADF中, ∴△ABG≌△ADF(SAS),∴AG=AF,∠GAB=∠DAF,∵∠EAF=45°,∴∠BAE+∠DAF=∠BAE+∠GAB=∠GAE=45°,∴∠EAF=∠GAE.在△AEG和△AEF中,∴△AEG≌△AEF(SAS).∴GE=EF,
设正方形的边长为x,DF=x-4,EC=x-3,GE=EF=BG+BE=DF+BE=x-4+3=x-1,
在Rt△EFC中,EF2=EC2+CF2,即(x-1)2=(x-3)2+42,解得x=6,即正方形的边长为6
【对应训练】
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( A )
A.2α B.90°-2α
C.45°-α D.90°-α
9.如图,正方形ABCD中,E是AD上一点,F是AB延长线上一点,DE=BF.点G,H分别在边AB,CD上,且GH=3,GH交EF于M.若∠EMH=45°,求EF的长.
解:连接CE,CF,如图,∵四边形ABCD是正方形,∴AB∥DC,BC=DC,∠ABC=∠D=90°,∴∠FBC=90°=∠D,在△FBC和△EDC中, ∴△FBC≌△EDC (SAS),∴CF=CE,∠FCB=∠ECD,∴∠ECF=∠ECB+∠FCB=∠ECB+∠ECD=90°,∴△CEF是等腰直角三角形,
∴∠EFC=45°,EF=CF,∵∠EMH=45°,
∴∠EFC=∠EMH,∴GH∥FC,∵AF∥DC,
∴四边形FCHG是平行四边形,∴CF=GH=3,
∴EF=CF=3
10.如图,在正方形ABCD中,点E为BC的中点,F为AB上一点,AE,CF交于点O.若AB=6,∠AOF=45°,求BF的长.
解:过点C作CM∥AE交AD于点M,延长AD到点N,使得DN=BF,连接CN,FM,如图所示,在正方形ABCD中,AD∥BC,AD=BC=CD,∠BAD=∠B=∠ADC=90°,∴∠NDC=∠B=90°,∴△NDC≌△FBC(SAS),∴CF=CN,∠DCN=∠BCF,
∵∠AOF=45°,CM∥AE,∴∠MCF=∠AOF=45°,∴∠MCN=∠MCD+∠DCN=45°,∴∠MCF=∠MCN,
在△MCF和△MCN中, ∴△MCF≌△MCN (SAS),∴MF=MN,∵AD∥BC,AE∥MC,∴四边形AECM是平行四边形,∴CE=AM,∵E是BC的中点,∴M是AD的中点,∵AB=6,∴AD=AB=6,∴AM=DM=3,设BF=x,则DN=x,AF=6-x,∴MF=MN=3+x,在Rt△AFM中,根据勾股定理,得32+(6-x)2=(3+x)2,解得x=2,∴BF=2
11.如图,在正方形ABCD中,E,F分别为边BC,CD上两点,∠EAF=45°.
(1)若EA是∠BEF的平分线,求证:FA是∠DFE的平分线;
(2)若BE=DF,求证:EF=BE+DF.
证明:(1)过点A作AH⊥EF于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°.
∵∠AHE=90°,∴∠B=∠AHE.
∵EA是∠BEF的平分线,
∴∠AEB=∠AEH.
在△ABE与△AHE中,
∴△ABE≌△AHE(AAS).∴AB=AH.
∵AB=AD,∴AH=AD.
在Rt△AHF与Rt△ADF中,
∴Rt△AHF≌Rt△ADF(HL).∴∠AFE=∠AFD.
∴FA是∠DFE的平分线.
证明:(2)如图,过点A作∠GAB=∠FAD,且G为CB边延长线上一点.
∵四边形ABCD为正方形,
∴∠D=∠ABC=90°,AB=AD.
∴∠ABG=90°.∴∠ABG=∠D.
在△GAB和△FAD中,
∴△GAB≌△FAD(ASA).∴BG=DF,AG=AF.
∵∠DAF+∠BAF=90°,∠GAB=∠FAD,
∴∠GAB+∠FAB=90°.∴∠GAF=90°.
∵∠EAF=45°,∴∠GAE=∠FAE=45°.
在△GAE和△FAE中,
∴△GAE≌△FAE(SAS).∴GE=EF.
∵GE=BG+BE,∴DF+BE=EF.
五、手拉手结构
【例5】如图,G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)若AB=3,AG=3,求EB的长.
解:(1)证明:∵四边形ABCD,
AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG.
∴∠EAB=∠GAD.
在△AEB和△AGD中,
∴△EAB≌△GAD(SAS).
解:(2)∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD==6.
∴∠DOG=90°,OA=OD=BD=3.
∵AG=3,∴OG=OA+AG=6.
∴GD===3.
∴EB=3.
