四川省成都市锦江区成都市七中育才学校2023-2024学年七年级下学期期中数学试题(无答案)
文档属性
| 名称 | 四川省成都市锦江区成都市七中育才学校2023-2024学年七年级下学期期中数学试题(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 640.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 00:00:00 | ||
图片预览

文档简介
成都七中育才学校2023-2024学年度(下)半期学业质量监测
七年级数学
(满分150分,时间120分钟)
A卷(100分)
一、选择题.(本大题共8个小题,每小题4分,共32分)
1.下列各式中计算正确的是( )
A. B. C. D.
2.世界上几乎所有的生物都是由细胞组成的,科学家发现,一个细胞的平均质量约为0.00000000011毫克.用科学记数法表示0.00000000011正确的是( )
A. B. C. D.
3.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm C.9cm,6cm,8cm D.3cm,4cm,5cm
4.如图,下列条件中,能判断的是( )
A. B. C. D.
5.下列乘法公式的运用中,正确的是( )
A. B.
C. D.
6.如果一个三角形的一个内角等于另外两个内角之和,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
7.给出下列说法:(1)在同一平面内,垂直于同一直线的两条直线互相平行;(2)相等的角是对顶角;(3)两条直线被第三条直线所截,同旁内角互补;(4)三角形的角平分线是线段.正确的共有( )
A.0个 B.1个 C.2个 D.3个
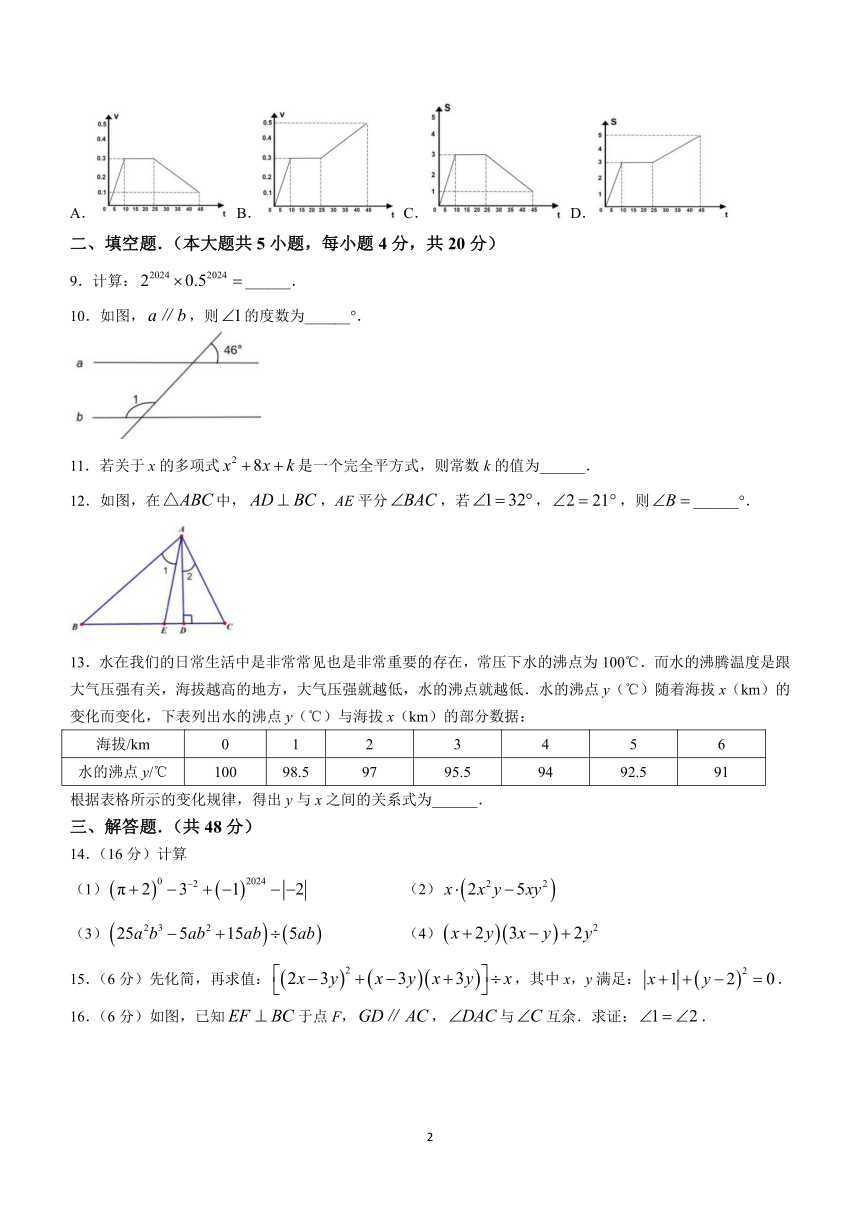
8.为了七中育才学校“四学会”活动顺利开展,小华老师提前去某基地做准备.他从学校骑共享自行车出发,先以0.3千米/分的速度匀速骑行10分钟,途经菜市场时,小华老师买水果花了15分钟.出了菜市场后,小华老师发现原来的共享自行车被其他人骑走,只能以0.1千米/分的速度步行前往基地,20分钟后小华老师到达基地.设小华老师的速度为v(千米/分),离校距离为s(千米),所用时间为t(分).下列图象能表达这一过程的是( )
A. B. C. D.
二、填空题.(本大题共5小题,每小题4分,共20分)
9.计算:______.
10.如图,,则的度数为______°.
11.若关于x的多项式是一个完全平方式,则常数k的值为______.
12.如图,在中,,AE平分,若,,则______°.
13.水在我们的日常生活中是非常常见也是非常重要的存在,常压下水的沸点为100℃.而水的沸腾温度是跟大气压强有关,海拔越高的地方,大气压强就越低,水的沸点就越低.水的沸点y(℃)随着海拔x(km)的变化而变化,下表列出水的沸点y(℃)与海拔x(km)的部分数据:
海拔/km 0 1 2 3 4 5 6
水的沸点y/℃ 100 98.5 97 95.5 94 92.5 91
根据表格所示的变化规律,得出y与x之间的关系式为______.
三、解答题.(共48分)
14.(16分)计算
(1) (2)
(3) (4)
15.(6分)先化简,再求值:,其中x,y满足:.
16.(6分)如图,已知于点F,,与互余.求证:.
证明:∵(已知)
∴(____________)
∴(____________)
∵与互余(已知)
∴
∴(____________)
∵(____________)
∴(____________)
∴(____________)
17.(10分)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为______米;李老师与家长聊天时间为______分钟;
(2)李老师的步行的速度是______米/分钟,跑步的速度是______米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
18.(10分)如图,直线,直线EF与AB,CD分别交于点G,H,.小明将一个含45°角的直角三角板PMN按如图①放置,使点N、M分别在直线AB,CD上,,.
(1)填空:______(填“>”“<”或“=”);
(2)若,射线NO在内交直线CD于点O,如图②.当N,M分别在点G,H的右侧,且,时,求的度数;
(3)小明将三角板PMN沿直线AB左右移动,保持,射线NO平分,点N,M分别在直线AB和直线CD上移动,请直接写出的度数(用含的式子表示).
B卷(50分)
一、填空题.(本大题共5小题,每小题4分,共20分)
19.已知,,则的值为______.
20.等腰三角形的两边长为4cm和8cm,这个三角形的周长为______cm.
21.若,则代数式______.
22.阅读材料:【材料1】将关于x的多项式用符号来表示,当时,该多项式的值就表示为.例如:,当时,该多项式的值为.【材料2】当一个多项式除以时,所得的余数就等于.例如,当多项式除以时,所得的余数就等于.根据以上材料回答问题:已知多项式,则______,除以时所得的余数等于______;已知多项式(m、n为常数),若除以时所得余数为7,除以时所得余数为3,则的值为______.
23.如图,在中,.现将沿过A点的一条直线折叠,使点B落在线段AC的延长线上的点E处,的角平分线与折痕交于点D,连接BD,DE.若中一个内角的度数是另一个内角度数的3倍,则的度数为______.
二、解答题.(本大题共3小题共30分)
24.(8分)某电力公司为了鼓励居民节约用电,采用分段计费的方法计算电费;第一档:每月用电不超过180度时,按每度0.5元计费;第二档:每月用电超过180度但不足280度时,其中超过部分按每度0.6元计费;第三档:280度以上时,超出部分按每度0.8元计费.
(1)若李明家1月份用电140度应交电费______元,2月份用电250度应交电费______元.
(2)若设某月用电量为x度,应交电费为y元,请求出y与x的关系式.并利用关系式求某月交电费120元时的用电量.
25.(10分)如图1,有A型、B型、C型三种不同的纸板,其中:A型:边长为a厘米的正方形;B型:边长为b厘米的正方形;C型:长为a厘米,宽为b厘米的长方形.
(1)取A型4块,B型4块,C型9块,此时纸板的总面积为______平方厘米;从这17块纸板中拿掉1块C型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为______平方厘米,这个大正方形的边长为______厘米;
(2)小明同学又用x张A型,y张B型,z张C型拼出了一个面积为的长方形,求的值.
(3)现将一个A型与一个B型拼成图2,且,求图2中阴影部分的面积.
26.(12分)已知中,BE平分.
(1)如图1,若点P在射线BE上,,并且平分,求的度数;
(2)如图2,在中,,BE平分,P为BE上一点,于P交CA延长线于点F,,,求的度数(用含m,n的代数式表示).
(3)如图3,的平分线交BE于点O,连接CO,过点O作交边AB于点D.作外角的平分线交BE于点P.若,将绕点A顺时针旋转一定角度后得,旋转后的三角形一边所在直线与PB平行,请直接写出所有符合条件的旋转角度的值.
七年级数学
(满分150分,时间120分钟)
A卷(100分)
一、选择题.(本大题共8个小题,每小题4分,共32分)
1.下列各式中计算正确的是( )
A. B. C. D.
2.世界上几乎所有的生物都是由细胞组成的,科学家发现,一个细胞的平均质量约为0.00000000011毫克.用科学记数法表示0.00000000011正确的是( )
A. B. C. D.
3.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm C.9cm,6cm,8cm D.3cm,4cm,5cm
4.如图,下列条件中,能判断的是( )
A. B. C. D.
5.下列乘法公式的运用中,正确的是( )
A. B.
C. D.
6.如果一个三角形的一个内角等于另外两个内角之和,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
7.给出下列说法:(1)在同一平面内,垂直于同一直线的两条直线互相平行;(2)相等的角是对顶角;(3)两条直线被第三条直线所截,同旁内角互补;(4)三角形的角平分线是线段.正确的共有( )
A.0个 B.1个 C.2个 D.3个
8.为了七中育才学校“四学会”活动顺利开展,小华老师提前去某基地做准备.他从学校骑共享自行车出发,先以0.3千米/分的速度匀速骑行10分钟,途经菜市场时,小华老师买水果花了15分钟.出了菜市场后,小华老师发现原来的共享自行车被其他人骑走,只能以0.1千米/分的速度步行前往基地,20分钟后小华老师到达基地.设小华老师的速度为v(千米/分),离校距离为s(千米),所用时间为t(分).下列图象能表达这一过程的是( )
A. B. C. D.
二、填空题.(本大题共5小题,每小题4分,共20分)
9.计算:______.
10.如图,,则的度数为______°.
11.若关于x的多项式是一个完全平方式,则常数k的值为______.
12.如图,在中,,AE平分,若,,则______°.
13.水在我们的日常生活中是非常常见也是非常重要的存在,常压下水的沸点为100℃.而水的沸腾温度是跟大气压强有关,海拔越高的地方,大气压强就越低,水的沸点就越低.水的沸点y(℃)随着海拔x(km)的变化而变化,下表列出水的沸点y(℃)与海拔x(km)的部分数据:
海拔/km 0 1 2 3 4 5 6
水的沸点y/℃ 100 98.5 97 95.5 94 92.5 91
根据表格所示的变化规律,得出y与x之间的关系式为______.
三、解答题.(共48分)
14.(16分)计算
(1) (2)
(3) (4)
15.(6分)先化简,再求值:,其中x,y满足:.
16.(6分)如图,已知于点F,,与互余.求证:.
证明:∵(已知)
∴(____________)
∴(____________)
∵与互余(已知)
∴
∴(____________)
∵(____________)
∴(____________)
∴(____________)
17.(10分)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为______米;李老师与家长聊天时间为______分钟;
(2)李老师的步行的速度是______米/分钟,跑步的速度是______米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
18.(10分)如图,直线,直线EF与AB,CD分别交于点G,H,.小明将一个含45°角的直角三角板PMN按如图①放置,使点N、M分别在直线AB,CD上,,.
(1)填空:______(填“>”“<”或“=”);
(2)若,射线NO在内交直线CD于点O,如图②.当N,M分别在点G,H的右侧,且,时,求的度数;
(3)小明将三角板PMN沿直线AB左右移动,保持,射线NO平分,点N,M分别在直线AB和直线CD上移动,请直接写出的度数(用含的式子表示).
B卷(50分)
一、填空题.(本大题共5小题,每小题4分,共20分)
19.已知,,则的值为______.
20.等腰三角形的两边长为4cm和8cm,这个三角形的周长为______cm.
21.若,则代数式______.
22.阅读材料:【材料1】将关于x的多项式用符号来表示,当时,该多项式的值就表示为.例如:,当时,该多项式的值为.【材料2】当一个多项式除以时,所得的余数就等于.例如,当多项式除以时,所得的余数就等于.根据以上材料回答问题:已知多项式,则______,除以时所得的余数等于______;已知多项式(m、n为常数),若除以时所得余数为7,除以时所得余数为3,则的值为______.
23.如图,在中,.现将沿过A点的一条直线折叠,使点B落在线段AC的延长线上的点E处,的角平分线与折痕交于点D,连接BD,DE.若中一个内角的度数是另一个内角度数的3倍,则的度数为______.
二、解答题.(本大题共3小题共30分)
24.(8分)某电力公司为了鼓励居民节约用电,采用分段计费的方法计算电费;第一档:每月用电不超过180度时,按每度0.5元计费;第二档:每月用电超过180度但不足280度时,其中超过部分按每度0.6元计费;第三档:280度以上时,超出部分按每度0.8元计费.
(1)若李明家1月份用电140度应交电费______元,2月份用电250度应交电费______元.
(2)若设某月用电量为x度,应交电费为y元,请求出y与x的关系式.并利用关系式求某月交电费120元时的用电量.
25.(10分)如图1,有A型、B型、C型三种不同的纸板,其中:A型:边长为a厘米的正方形;B型:边长为b厘米的正方形;C型:长为a厘米,宽为b厘米的长方形.
(1)取A型4块,B型4块,C型9块,此时纸板的总面积为______平方厘米;从这17块纸板中拿掉1块C型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.剩下纸板的总面积为______平方厘米,这个大正方形的边长为______厘米;
(2)小明同学又用x张A型,y张B型,z张C型拼出了一个面积为的长方形,求的值.
(3)现将一个A型与一个B型拼成图2,且,求图2中阴影部分的面积.
26.(12分)已知中,BE平分.
(1)如图1,若点P在射线BE上,,并且平分,求的度数;
(2)如图2,在中,,BE平分,P为BE上一点,于P交CA延长线于点F,,,求的度数(用含m,n的代数式表示).
(3)如图3,的平分线交BE于点O,连接CO,过点O作交边AB于点D.作外角的平分线交BE于点P.若,将绕点A顺时针旋转一定角度后得,旋转后的三角形一边所在直线与PB平行,请直接写出所有符合条件的旋转角度的值.
同课章节目录
