高中数学人教A版(2019)必修2 9.2.1 总体取值规律的估计 第2课时(24页ppt)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 9.2.1 总体取值规律的估计 第2课时(24页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 08:47:30 | ||
图片预览



文档简介
(共24张PPT)
第九章
9.2.1 总体取值规律的估计 第2课时
人教A版(2019)
教学目标
学习目标 数学素养
1.掌握常用三种统计图表(条形统计图、扇形统计图、折线统计图)的功能及特点. 1.数据分析素养.
2.能针对实际问题好收集的数据的特点,选择科学的统计图表,能从统计图表中获取有价值的信息. 2.数据分析素养和运算素养.
温故知新
1.求极差
2.决定组距和组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
绘制频率分布直方图的步骤
一组数据中最大值与最小值的差
组数若则组数若则组数为不小于的最小整数
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
频数分布表与频率分布直方图的不同
频数分布表能使我们清楚地知道数据分布在各个小组的个数,而频率分布直方图则是从各个小组数据在样本容量中所占比例大小的角度来表示数据分布的规律.
温故知新
除频率分布直方图外,我们在初中还学习过条形图、扇形图、折线图、频数分布直方图等.不同的统计图在表示数据上有不同的特点.
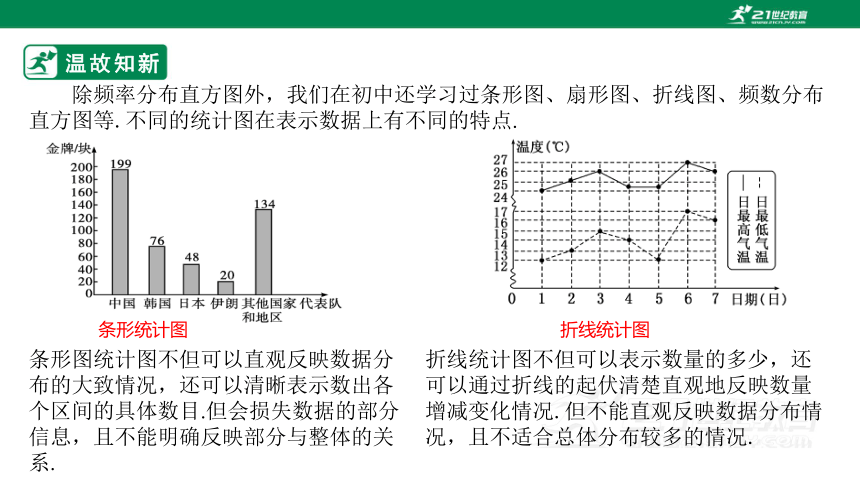
条形统计图
条形图统计图不但可以直观反映数据分布的大致情况,还可以清晰表示数出各个区间的具体数目.但会损失数据的部分信息,且不能明确反映部分与整体的关系.
折线统计图
折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地反映数量增减变化情况.但不能直观反映数据分布情况,且不适合总体分布较多的情况.
温故知新
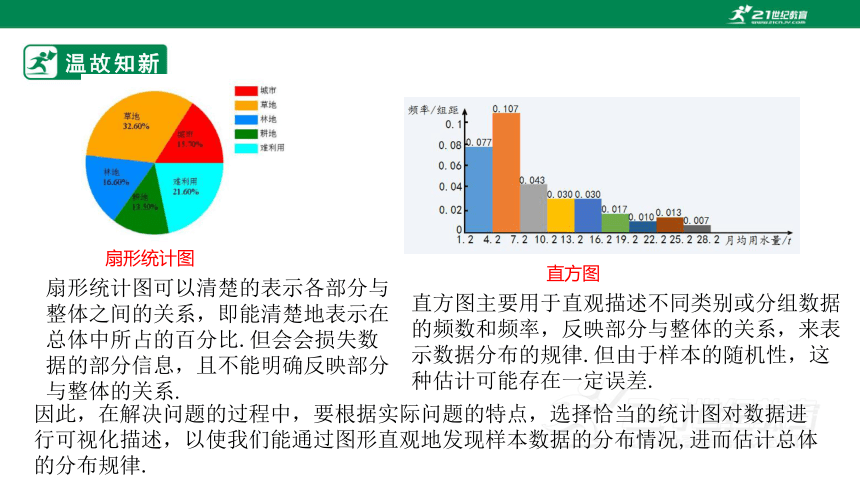
扇形统计图可以清楚的表示各部分与整体之间的关系,即能清楚地表示在总体中所占的百分比.但会会损失数据的部分信息,且不能明确反映部分与整体的关系.
扇形统计图
直方图
直方图主要用于直观描述不同类别或分组数据的频数和频率,反映部分与整体的关系,来表示数据分布的规律.但由于样本的随机性,这种估计可能存在一定误差.
因此,在解决问题的过程中,要根据实际问题的特点,选择恰当的统计图对数据进行可视化描述,以使我们能通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律.
知新探究
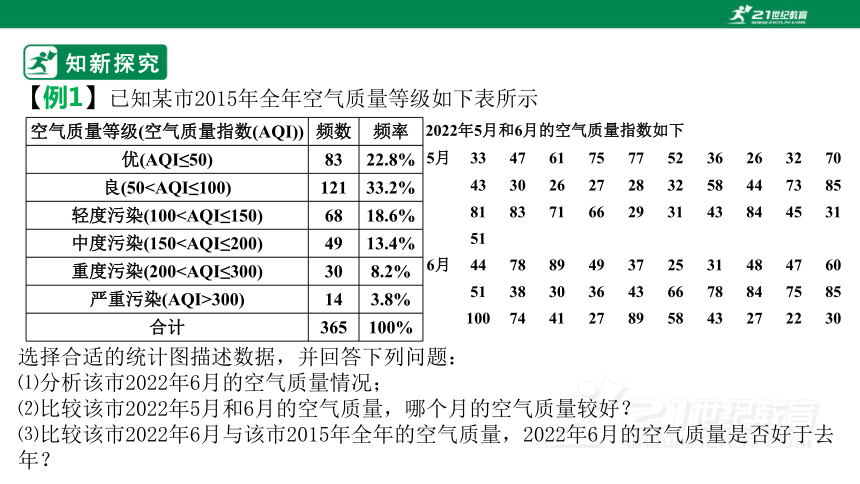
【例1】已知某市2015年全年空气质量等级如下表所示
选择合适的统计图描述数据,并回答下列问题:
⑴分析该市2022年6月的空气质量情况;
⑵比较该市2022年5月和6月的空气质量,哪个月的空气质量较好?
⑶比较该市2022年6月与该市2015年全年的空气质量,2022年6月的空气质量是否好于去年?
空气质量等级(空气质量指数(AQI)) 频数 频率
优(AQI≤50) 83 22.8%
良(50轻度污染(100中度污染(150重度污染(200严重污染(AQI>300) 14 3.8%
合计 365 100%
2022年5月和6月的空气质量指数如下 5月 33 47 61 75 77 52 36 26 32 70
43 30 26 27 28 32 58 44 73 85
81 83 71 66 29 31 43 84 45 31
51
6月 44 78 89 49 37 25 31 48 47 60
51 38 30 36 43 66 78 84 75 85
100 74 41 27 89 58 43 27 22 30
知新探究
解:
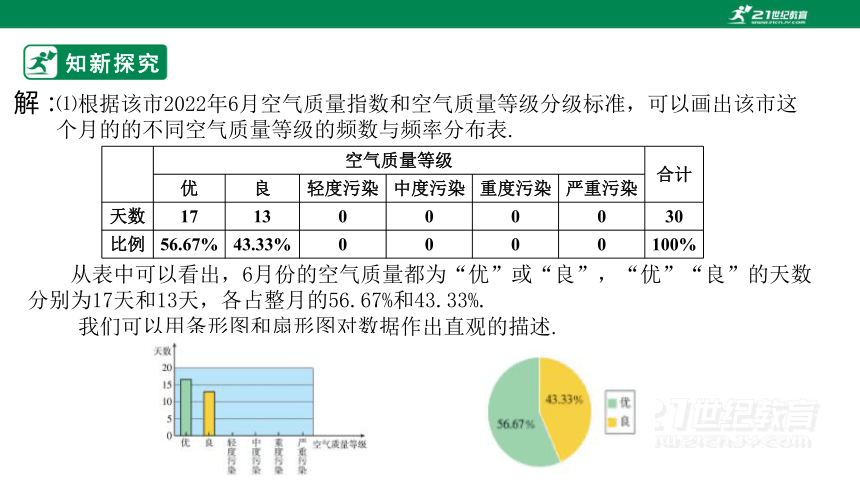
⑴根据该市2022年6月空气质量指数和空气质量等级分级标准,可以画出该市这个月的的不同空气质量等级的频数与频率分布表.
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 13 0 0 0 0 30
比例 56.67% 43.33% 0 0 0 0 100%
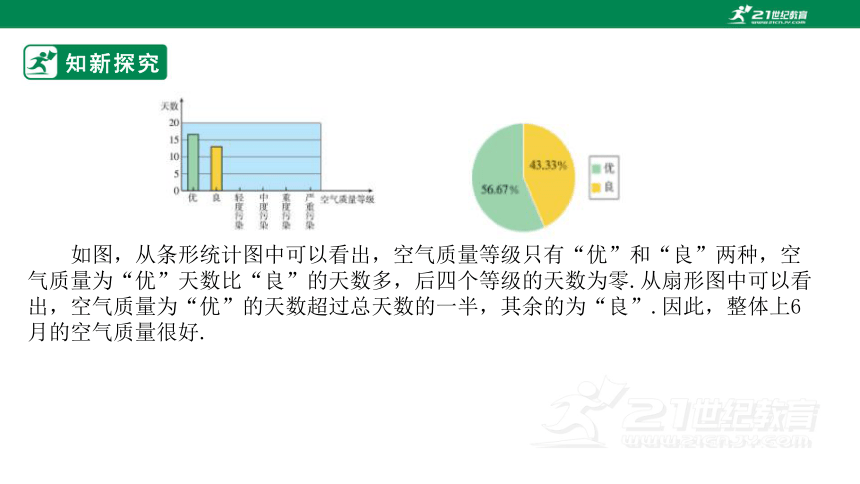
从表中可以看出,6月份的空气质量都为“优”或“良”,“优”“良”的天数分别为17天和13天,各占整月的56.67%和43.33%.
我们可以用条形图和扇形图对数据作出直观的描述.
知新探究
如图,从条形统计图中可以看出,空气质量等级只有“优”和“良”两种,空气质量为“优”天数比“良”的天数多,后四个等级的天数为零.从扇形图中可以看出,空气质量为“优”的天数超过总天数的一半,其余的为“良”.因此,整体上6月的空气质量很好.
知新探究
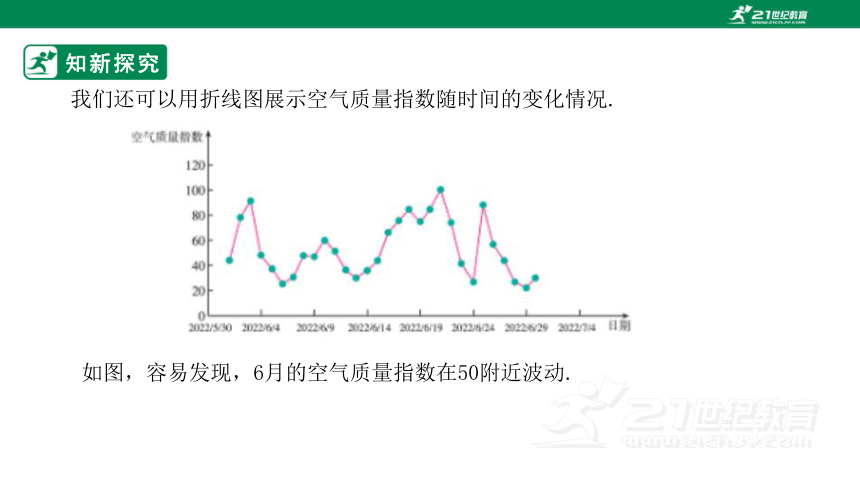
我们还可以用折线图展示空气质量指数随时间的变化情况.
如图,容易发现,6月的空气质量指数在50附近波动.
知新探究
解:
⑵根据该市2022年6月空气质量指数和空气质量等级分级标准,可以画出该市这个月的的不同空气质量等级的频数与频率分布表.
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 14 0 0 0 0 31
比例 54.84% 45.16% 0 0 0 0 100%
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上.通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较.
知新探究
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 14 0 0 0 0 31
比例 54.84% 45.16% 0 0 0 0 100%
由表和图可以发现,5月和6月空气质量基本相同.“优”的天数相同,均为17天,5月“良”的天数比6月多1天,两个月均没有为轻度污染以上的天数.
知新探究
解:
⑶把2022年6月和2015年全年的空气质量进行比较,由于一个月和一年的天数差别很大,所以直接通过频数比较没有意义,应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较.
通过上图可以看出,虽然2022年6月的空气质量为“优”和“良”的频率明显高于2015年,而且2022年6月空气质量为污染天气频率为0,明显小于2015年.所以从整体上看,2022年6月的空气质量明显好于2015年全年的空气质量.
由此,你能得出“2022年的空气质量比2015年明显改善了 ”的结论吗?为什么
知新探究
【例2】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶供学生饮用.中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如下两张不完整的人数统计图:
选择合适的统计图描述数据,并回答下列问题:
⑴本次被调查的学生有多少名?
⑵补全右面的条形统计图⑴,并计算出喜好菠萝味牛奶的学生人数在扇形统计图⑵中所占圆心角的度数;
知新探究
解:
⑴由条形统计图和扇形统计图可知,喜好核桃味的学生人数为10名,占被调查学生的5%,则被调查学生人数为
10÷5%=200(名)
⑵右面的条形统计图⑴补全如下:
喜好菠萝味牛奶的学生人数在扇形统计图(2)中所占圆心角的度数为
.
知新探究
⑶该校共有1 200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味的多送多少盒?
解:
⑶草莓味要比原味的盒数为
×(62-38)=144(盒).
初试身手
1.甲、乙两个城市2020年4月中旬每天的最高气温统计图如图所示,则这9天里,气温比较稳定的是________(选填“甲”或“乙”)城市.
解:
由折线统计图可知,这9天里,甲城市气温比较稳定.
甲
初试身手
2.某校为了了解高三学生的身体状况,抽取了100名
女生的体重.将所得的数据整理后,画出了如图的频
率分布直方图,则所抽取的女生中体重在40~45 kg
的人数是( )
A.10 B.2 C.5 D.15
解:
由题意及频率分布直方图可知,频率=×组距.
体重在40~45 kg的女生的频率=0.02×5=0.1.
∴女生中体重在40~45 kg的人数为0.1×100=10.
初试身手
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
⑴该厂第一季度 月的产量最高;
⑵该厂一月份产量占第一季度总产量的 %;
解:
⑴由条形图可知,三月的产量最高;
三
⑵该厂一月份产量占第一季度总产量的1-38%-32%=30%;
30
初试身手
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
⑶该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计该厂第一季度生产了多少件合格的产品
解:
⑶该厂第一季度共生产1 900÷38%=5 000(件)产品.
答:该厂第一季度大约生产了4 900件合格的产品.
∵合格率为98%,
∴合格的产品有5 000×98%=4 900(件).
课堂小结
1.常见统计图表的特点.
条形图统计图不但可以直观反映数据分布的大致情况,还可以清晰表示数出各个区间的具体数目.但会损失数据的部分信息,且不能明确反映部分与整体的关系.
折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地反映数量增减变化情况.但不能直观反映数据分布情况,且不适合总体分布较多的情况.
扇形统计图可以清楚的表示各部分与整体之间的关系,即能清楚地表示在总体中所占的百分比.但会会损失数据的部分信息,且不能明确反映部分与整体的关系.
直方图主要用于直观描述不同类别或分组数据的频数和频率,反映部分与整体的关系,来表示数据分布的规律.但由于样本的随机性,这种估计可能存在一定误差.
2.扇形图、条形图和折线图的应用.
在解决问题的过程中,要根据实际问题的特点,选择恰当的统计图对数据进行可视化描述,以使我们能通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律.
作业布置
作业: P202 练习 第1题.
补充:
1.如图是甲、乙、丙、丁四组人数的扇形统计图的部分结
果,根据扇形统计图的情况可以知道丙、丁两组人数和
为( )
A.250 B.150 C.400 D.300
2.200辆汽车经过某一雷达地区,时速的频率分布直
方图如图所示,则时速超过60 km/h(含60 km/h)的汽
车数量为( )
A.65辆 B.76辆 C.88辆 D.95辆
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第九章
9.2.1 总体取值规律的估计 第2课时
人教A版(2019)
教学目标
学习目标 数学素养
1.掌握常用三种统计图表(条形统计图、扇形统计图、折线统计图)的功能及特点. 1.数据分析素养.
2.能针对实际问题好收集的数据的特点,选择科学的统计图表,能从统计图表中获取有价值的信息. 2.数据分析素养和运算素养.
温故知新
1.求极差
2.决定组距和组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
绘制频率分布直方图的步骤
一组数据中最大值与最小值的差
组数若则组数若则组数为不小于的最小整数
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
频数分布表与频率分布直方图的不同
频数分布表能使我们清楚地知道数据分布在各个小组的个数,而频率分布直方图则是从各个小组数据在样本容量中所占比例大小的角度来表示数据分布的规律.
温故知新
除频率分布直方图外,我们在初中还学习过条形图、扇形图、折线图、频数分布直方图等.不同的统计图在表示数据上有不同的特点.
条形统计图
条形图统计图不但可以直观反映数据分布的大致情况,还可以清晰表示数出各个区间的具体数目.但会损失数据的部分信息,且不能明确反映部分与整体的关系.
折线统计图
折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地反映数量增减变化情况.但不能直观反映数据分布情况,且不适合总体分布较多的情况.
温故知新
扇形统计图可以清楚的表示各部分与整体之间的关系,即能清楚地表示在总体中所占的百分比.但会会损失数据的部分信息,且不能明确反映部分与整体的关系.
扇形统计图
直方图
直方图主要用于直观描述不同类别或分组数据的频数和频率,反映部分与整体的关系,来表示数据分布的规律.但由于样本的随机性,这种估计可能存在一定误差.
因此,在解决问题的过程中,要根据实际问题的特点,选择恰当的统计图对数据进行可视化描述,以使我们能通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律.
知新探究
【例1】已知某市2015年全年空气质量等级如下表所示
选择合适的统计图描述数据,并回答下列问题:
⑴分析该市2022年6月的空气质量情况;
⑵比较该市2022年5月和6月的空气质量,哪个月的空气质量较好?
⑶比较该市2022年6月与该市2015年全年的空气质量,2022年6月的空气质量是否好于去年?
空气质量等级(空气质量指数(AQI)) 频数 频率
优(AQI≤50) 83 22.8%
良(50
合计 365 100%
2022年5月和6月的空气质量指数如下 5月 33 47 61 75 77 52 36 26 32 70
43 30 26 27 28 32 58 44 73 85
81 83 71 66 29 31 43 84 45 31
51
6月 44 78 89 49 37 25 31 48 47 60
51 38 30 36 43 66 78 84 75 85
100 74 41 27 89 58 43 27 22 30
知新探究
解:
⑴根据该市2022年6月空气质量指数和空气质量等级分级标准,可以画出该市这个月的的不同空气质量等级的频数与频率分布表.
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 13 0 0 0 0 30
比例 56.67% 43.33% 0 0 0 0 100%
从表中可以看出,6月份的空气质量都为“优”或“良”,“优”“良”的天数分别为17天和13天,各占整月的56.67%和43.33%.
我们可以用条形图和扇形图对数据作出直观的描述.
知新探究
如图,从条形统计图中可以看出,空气质量等级只有“优”和“良”两种,空气质量为“优”天数比“良”的天数多,后四个等级的天数为零.从扇形图中可以看出,空气质量为“优”的天数超过总天数的一半,其余的为“良”.因此,整体上6月的空气质量很好.
知新探究
我们还可以用折线图展示空气质量指数随时间的变化情况.
如图,容易发现,6月的空气质量指数在50附近波动.
知新探究
解:
⑵根据该市2022年6月空气质量指数和空气质量等级分级标准,可以画出该市这个月的的不同空气质量等级的频数与频率分布表.
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 14 0 0 0 0 31
比例 54.84% 45.16% 0 0 0 0 100%
为了便于比较,我们选用复合条形图,将两组数据同时反映到一个条形图上.通过条形图中柱的高低,可以更直观地进行两个月的空气质量的比较.
知新探究
空气质量等级 合计
优 良 轻度污染 中度污染 重度污染 严重污染 天数 17 14 0 0 0 0 31
比例 54.84% 45.16% 0 0 0 0 100%
由表和图可以发现,5月和6月空气质量基本相同.“优”的天数相同,均为17天,5月“良”的天数比6月多1天,两个月均没有为轻度污染以上的天数.
知新探究
解:
⑶把2022年6月和2015年全年的空气质量进行比较,由于一个月和一年的天数差别很大,所以直接通过频数比较没有意义,应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较.
通过上图可以看出,虽然2022年6月的空气质量为“优”和“良”的频率明显高于2015年,而且2022年6月空气质量为污染天气频率为0,明显小于2015年.所以从整体上看,2022年6月的空气质量明显好于2015年全年的空气质量.
由此,你能得出“2022年的空气质量比2015年明显改善了 ”的结论吗?为什么
知新探究
【例2】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶供学生饮用.中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如下两张不完整的人数统计图:
选择合适的统计图描述数据,并回答下列问题:
⑴本次被调查的学生有多少名?
⑵补全右面的条形统计图⑴,并计算出喜好菠萝味牛奶的学生人数在扇形统计图⑵中所占圆心角的度数;
知新探究
解:
⑴由条形统计图和扇形统计图可知,喜好核桃味的学生人数为10名,占被调查学生的5%,则被调查学生人数为
10÷5%=200(名)
⑵右面的条形统计图⑴补全如下:
喜好菠萝味牛奶的学生人数在扇形统计图(2)中所占圆心角的度数为
.
知新探究
⑶该校共有1 200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味的多送多少盒?
解:
⑶草莓味要比原味的盒数为
×(62-38)=144(盒).
初试身手
1.甲、乙两个城市2020年4月中旬每天的最高气温统计图如图所示,则这9天里,气温比较稳定的是________(选填“甲”或“乙”)城市.
解:
由折线统计图可知,这9天里,甲城市气温比较稳定.
甲
初试身手
2.某校为了了解高三学生的身体状况,抽取了100名
女生的体重.将所得的数据整理后,画出了如图的频
率分布直方图,则所抽取的女生中体重在40~45 kg
的人数是( )
A.10 B.2 C.5 D.15
解:
由题意及频率分布直方图可知,频率=×组距.
体重在40~45 kg的女生的频率=0.02×5=0.1.
∴女生中体重在40~45 kg的人数为0.1×100=10.
初试身手
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
⑴该厂第一季度 月的产量最高;
⑵该厂一月份产量占第一季度总产量的 %;
解:
⑴由条形图可知,三月的产量最高;
三
⑵该厂一月份产量占第一季度总产量的1-38%-32%=30%;
30
初试身手
3.某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:
⑶该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计该厂第一季度生产了多少件合格的产品
解:
⑶该厂第一季度共生产1 900÷38%=5 000(件)产品.
答:该厂第一季度大约生产了4 900件合格的产品.
∵合格率为98%,
∴合格的产品有5 000×98%=4 900(件).
课堂小结
1.常见统计图表的特点.
条形图统计图不但可以直观反映数据分布的大致情况,还可以清晰表示数出各个区间的具体数目.但会损失数据的部分信息,且不能明确反映部分与整体的关系.
折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地反映数量增减变化情况.但不能直观反映数据分布情况,且不适合总体分布较多的情况.
扇形统计图可以清楚的表示各部分与整体之间的关系,即能清楚地表示在总体中所占的百分比.但会会损失数据的部分信息,且不能明确反映部分与整体的关系.
直方图主要用于直观描述不同类别或分组数据的频数和频率,反映部分与整体的关系,来表示数据分布的规律.但由于样本的随机性,这种估计可能存在一定误差.
2.扇形图、条形图和折线图的应用.
在解决问题的过程中,要根据实际问题的特点,选择恰当的统计图对数据进行可视化描述,以使我们能通过图形直观地发现样本数据的分布情况,进而估计总体的分布规律.
作业布置
作业: P202 练习 第1题.
补充:
1.如图是甲、乙、丙、丁四组人数的扇形统计图的部分结
果,根据扇形统计图的情况可以知道丙、丁两组人数和
为( )
A.250 B.150 C.400 D.300
2.200辆汽车经过某一雷达地区,时速的频率分布直
方图如图所示,则时速超过60 km/h(含60 km/h)的汽
车数量为( )
A.65辆 B.76辆 C.88辆 D.95辆
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
