五年级上册数学青岛版第1讲:比比速算课件(共22张PPT)
文档属性
| 名称 | 五年级上册数学青岛版第1讲:比比速算课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-01 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
讲故事
比比速算
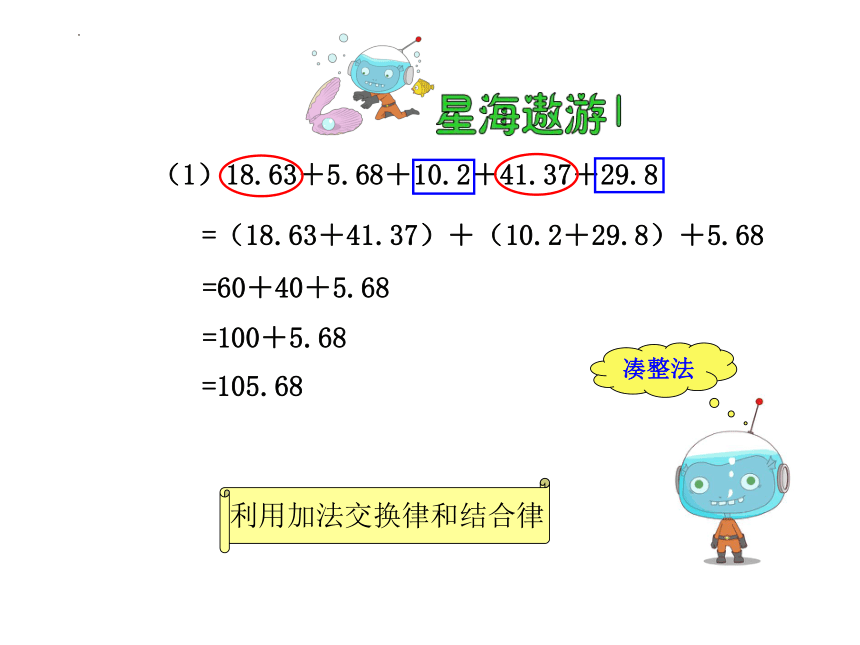
(1)18.63+5.68+10.2+41.37+29.8
凑整法
=(18.63+41.37)+(10.2+29.8)+5.68
利用加法交换律和结合律
=60+40+5.68
=100+5.68
=105.68
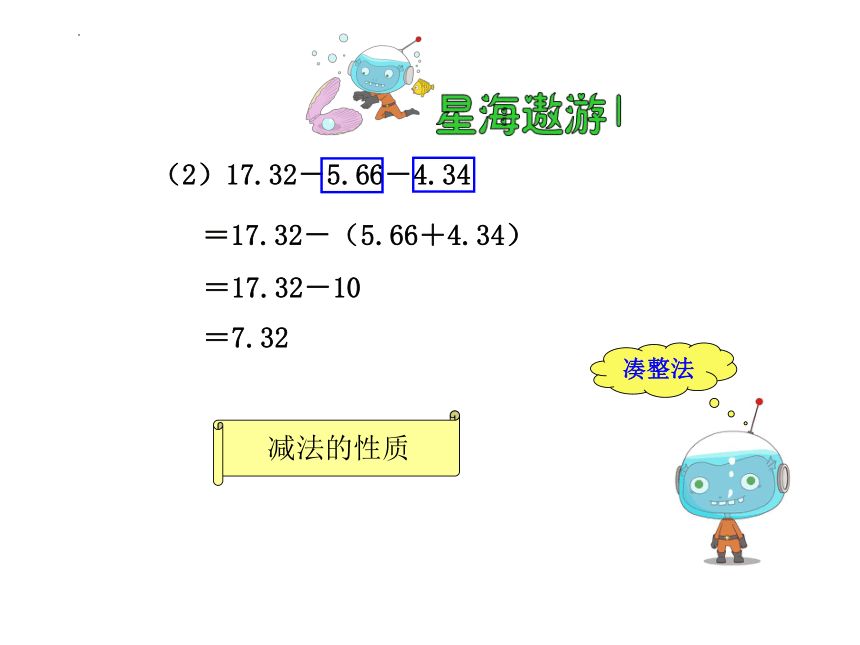
(2)17.32-5.66-4.34
凑整法
=17.32-(5.66+4.34)
减法的性质
=17.32-10
=7.32
4.3+2.18+5.7+7.82
凑整法
=(4.3+5.7)+(2.18+7.82)
利用加法交换律和结合律
= 10+10
= 20
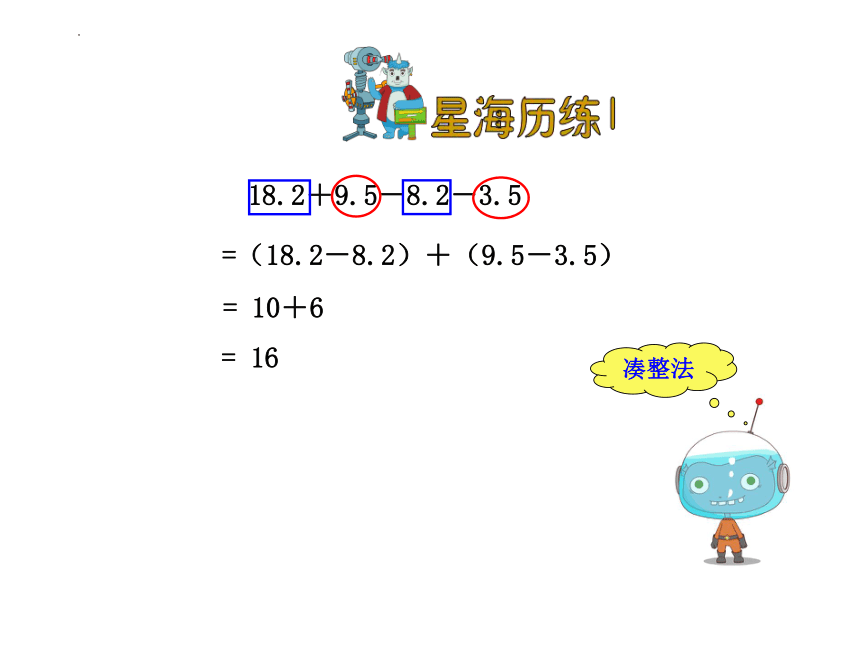
18.2+9.5-8.2-3.5
凑整法
=(18.2-8.2)+(9.5-3.5)
= 10+6
= 16
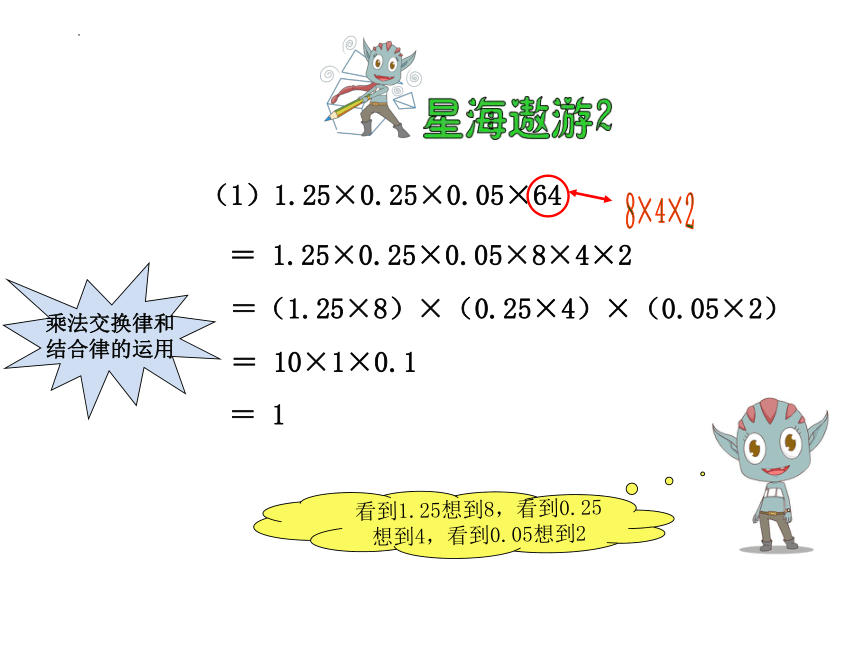
(1)1.25×0.25×0.05×64
8×4×2
看到1.25想到8,看到0.25
想到4,看到0.05想到2
= 1.25×0.25×0.05×8×4×2
乘法交换律和
结合律的运用
=(1.25×8)×(0.25×4)×(0.05×2)
= 10×1×0.1
= 1
(2)49÷3.5÷2
=49÷(3.5×2)
=49÷7
=7
凑整法
除法的性质
速算的方法有:
(1)利用加法交换律,加法结合律,乘法交换律,乘法
结合律,使题目中的数字凑成整数,计算起来会更
简便。
(2)利用减法的性质、除法的性质来做,主要也是使题
目中的数字凑整。
(3)记住一些特殊的等式,使计算简便。
1.31×12.5×0.15×8×2
看到12.5想到8,看到0.15想到2
= 1.31×(12.5×8)×(0.15×2)
乘法交换律和
结合律的运用
= 1.31×100×0.3
= 39.3
1÷64÷0.05÷0.25÷0.125
除法的性质
8×4×2
=1÷(64×0.05×0.25×0.125)
看到0.125想到8,看到0.25
想到4,看到0.05想到2
=1÷(2×0.05×4×0.25×8×0.125)
=1÷0.1
=10
1. 0.25+0.47+4.75+9.53
看谁最厉害!
2. 5.42-1.26-3.74
3. 125×4×25×8
4. 77×4.8-72×4.8
77×4.8-72×4.8
乘法分配律的逆运算
=(77-72)×4.8
= 5×4.8
= 24
2.25×0.16+264×0.0225+5.2×2.25+0.225×20
把四个因数变成一样的
=0.225×1.6+26.4×0.225+52×0.225+0.225×20
=0.225×(1.6+26.4+52+20)
=0.225×100
乘法分配律的逆运用
=22.5
4.82×0.59+0.41×1.59-0.323×5.9
把2个因数变成一样的
=4.82×0.59-3.23×0.59+0.41×1.59
=(4.82-3.23)×0.59+0.41×1.59
=1.59×0.59+0.41×1.59
乘法分配律的逆运用
=(0.59+0.41)×1.59
=1.59
41.2×8.1+11×9.25+537×0.19
使因数变成一样的
=412×0.81+537×0.19+11×9.25
=412×0.81+(412+125)×0.19+11×9.25
=412×0.81+412×0.19+125×0.19+11×9.25
乘法分配律的逆运用
=412×(0.81+0.19)+125×0.19+11×(1.25+8)
412+125
=412+1.25×19+11×1.25+11×8
=412+1.25×(19+11)+88
=412+1.25×30+88
=537.5
1.234×3456.7+0.1234×12345+0.01234×530880
把三个因数变成一样的
=1.234×3456.7+1.234×1234.5+1.234×5308.8
=1.234×(3456.7+1234.5+5308.8)
=1.234×10000
乘法分配律的逆运用
=12340
0.4444+2.222×2222.2+17777.6×2.222
2.222×0.2
乘法分配律的逆运用
=0.4444+2.222×(2222.2+17777.6)
=0.4444+2.222×19999.8
=2.222×0.2+2.222×19999.8
=2.222×(0.2+19999.8)
=2.222×20000
=44440
(2.15+5.17+3.62)×(5.17+2.15+8.5)-(3.62+2.15+8.5
+5.17)×(2.15+5.17)
假设法
设a=2.15+5.17+3.62 b=2.15+5.17
原式=a×(8.5+b)-(a+8.5)×b
=8.5a+ab-ab-8.5b
=8.5×(a-b)
乘法分配律
=8.5×3.62
=30.77
(2+3.15+5.87)×(3.15+5.87+7.32)-(2+3.15+
5.87+7.32)×(3.15+5.87)
假设法
设a=2+3.15+5.87 b=3.15+5.87
原式=a×(b+7.32)-(a+7.32)×b
=ab+7.32a-ab-7.32b
=7.32×(a-b)
乘法分配律
=7.32×2
=14.64
(1+0.12+0.23)×(0.12+0.23+0.34)-(1+0.12+
0.23+0.34)×(0.12+0.23)
假设法
设a=1+0.12+0.23 b=0.12+0.23
原式=a×(b+0.34)-(a+0.34)×b
=ab+0.34a-ab-0.34b
=0.34×(a-b)
乘法分配律
=0.34×1
=0.34
速算的方法很多,这节课主要讲了两种方法:
(1)乘法分配律的逆运用:a×b+a×c=a×(b+c)或者a×b-a×c=a×(b-c)
(2)假设法:用一个字母代替几个数的运算,这样使计算简便。
讲故事
比比速算
(1)18.63+5.68+10.2+41.37+29.8
凑整法
=(18.63+41.37)+(10.2+29.8)+5.68
利用加法交换律和结合律
=60+40+5.68
=100+5.68
=105.68
(2)17.32-5.66-4.34
凑整法
=17.32-(5.66+4.34)
减法的性质
=17.32-10
=7.32
4.3+2.18+5.7+7.82
凑整法
=(4.3+5.7)+(2.18+7.82)
利用加法交换律和结合律
= 10+10
= 20
18.2+9.5-8.2-3.5
凑整法
=(18.2-8.2)+(9.5-3.5)
= 10+6
= 16
(1)1.25×0.25×0.05×64
8×4×2
看到1.25想到8,看到0.25
想到4,看到0.05想到2
= 1.25×0.25×0.05×8×4×2
乘法交换律和
结合律的运用
=(1.25×8)×(0.25×4)×(0.05×2)
= 10×1×0.1
= 1
(2)49÷3.5÷2
=49÷(3.5×2)
=49÷7
=7
凑整法
除法的性质
速算的方法有:
(1)利用加法交换律,加法结合律,乘法交换律,乘法
结合律,使题目中的数字凑成整数,计算起来会更
简便。
(2)利用减法的性质、除法的性质来做,主要也是使题
目中的数字凑整。
(3)记住一些特殊的等式,使计算简便。
1.31×12.5×0.15×8×2
看到12.5想到8,看到0.15想到2
= 1.31×(12.5×8)×(0.15×2)
乘法交换律和
结合律的运用
= 1.31×100×0.3
= 39.3
1÷64÷0.05÷0.25÷0.125
除法的性质
8×4×2
=1÷(64×0.05×0.25×0.125)
看到0.125想到8,看到0.25
想到4,看到0.05想到2
=1÷(2×0.05×4×0.25×8×0.125)
=1÷0.1
=10
1. 0.25+0.47+4.75+9.53
看谁最厉害!
2. 5.42-1.26-3.74
3. 125×4×25×8
4. 77×4.8-72×4.8
77×4.8-72×4.8
乘法分配律的逆运算
=(77-72)×4.8
= 5×4.8
= 24
2.25×0.16+264×0.0225+5.2×2.25+0.225×20
把四个因数变成一样的
=0.225×1.6+26.4×0.225+52×0.225+0.225×20
=0.225×(1.6+26.4+52+20)
=0.225×100
乘法分配律的逆运用
=22.5
4.82×0.59+0.41×1.59-0.323×5.9
把2个因数变成一样的
=4.82×0.59-3.23×0.59+0.41×1.59
=(4.82-3.23)×0.59+0.41×1.59
=1.59×0.59+0.41×1.59
乘法分配律的逆运用
=(0.59+0.41)×1.59
=1.59
41.2×8.1+11×9.25+537×0.19
使因数变成一样的
=412×0.81+537×0.19+11×9.25
=412×0.81+(412+125)×0.19+11×9.25
=412×0.81+412×0.19+125×0.19+11×9.25
乘法分配律的逆运用
=412×(0.81+0.19)+125×0.19+11×(1.25+8)
412+125
=412+1.25×19+11×1.25+11×8
=412+1.25×(19+11)+88
=412+1.25×30+88
=537.5
1.234×3456.7+0.1234×12345+0.01234×530880
把三个因数变成一样的
=1.234×3456.7+1.234×1234.5+1.234×5308.8
=1.234×(3456.7+1234.5+5308.8)
=1.234×10000
乘法分配律的逆运用
=12340
0.4444+2.222×2222.2+17777.6×2.222
2.222×0.2
乘法分配律的逆运用
=0.4444+2.222×(2222.2+17777.6)
=0.4444+2.222×19999.8
=2.222×0.2+2.222×19999.8
=2.222×(0.2+19999.8)
=2.222×20000
=44440
(2.15+5.17+3.62)×(5.17+2.15+8.5)-(3.62+2.15+8.5
+5.17)×(2.15+5.17)
假设法
设a=2.15+5.17+3.62 b=2.15+5.17
原式=a×(8.5+b)-(a+8.5)×b
=8.5a+ab-ab-8.5b
=8.5×(a-b)
乘法分配律
=8.5×3.62
=30.77
(2+3.15+5.87)×(3.15+5.87+7.32)-(2+3.15+
5.87+7.32)×(3.15+5.87)
假设法
设a=2+3.15+5.87 b=3.15+5.87
原式=a×(b+7.32)-(a+7.32)×b
=ab+7.32a-ab-7.32b
=7.32×(a-b)
乘法分配律
=7.32×2
=14.64
(1+0.12+0.23)×(0.12+0.23+0.34)-(1+0.12+
0.23+0.34)×(0.12+0.23)
假设法
设a=1+0.12+0.23 b=0.12+0.23
原式=a×(b+0.34)-(a+0.34)×b
=ab+0.34a-ab-0.34b
=0.34×(a-b)
乘法分配律
=0.34×1
=0.34
速算的方法很多,这节课主要讲了两种方法:
(1)乘法分配律的逆运用:a×b+a×c=a×(b+c)或者a×b-a×c=a×(b-c)
(2)假设法:用一个字母代替几个数的运算,这样使计算简便。
同课章节目录
