四年级下册数学冀教版第二单元 用字母表示数量关系课件(共30张PPT)
文档属性
| 名称 | 四年级下册数学冀教版第二单元 用字母表示数量关系课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-01 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
第二单元 用字母表示数
1.用字母表示数量关系
麦当劳
停车场
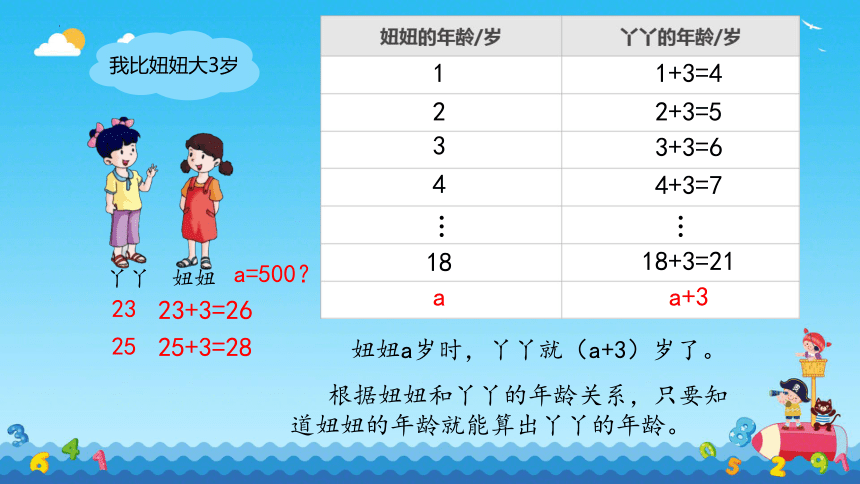
妞妞
丫丫
我比妞妞大3岁
a
23+3=26
a+3
1+3=4
2+3=5
3+3=6
18+3=21
1
2
3
…
…
4
妞妞a岁时,丫丫就(a+3)岁了。
18
4+3=7
根据妞妞和丫丫的年龄关系,只要知道妞妞的年龄就能算出丫丫的年龄。
23
25+3=28
25
a=500?
例2:用含有字母的式子表示买 铅笔盒的钱数。
买3个铅笔盒需要( )元;
买5个铅笔盒需要( )元;
买18个铅笔盒需要( )元;
买a个铅笔盒需要( )元;
3×9=27
5×9=45
18×9=162
9×a
省略乘号时,一般把数写在字母的前面
x+y
2x+2y
3x+y
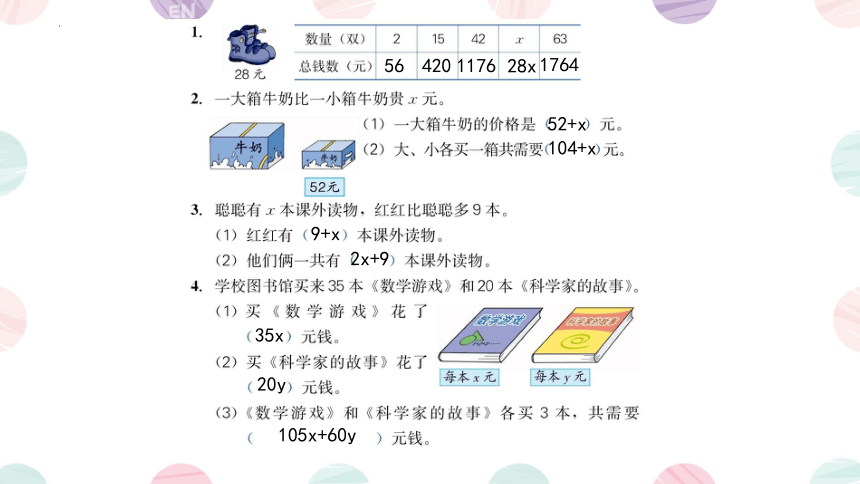
52+x
56
420
1176
28x
1764
104+x
9+x
2x+9
35x
20y
105x+60y
2.用字母表示公式
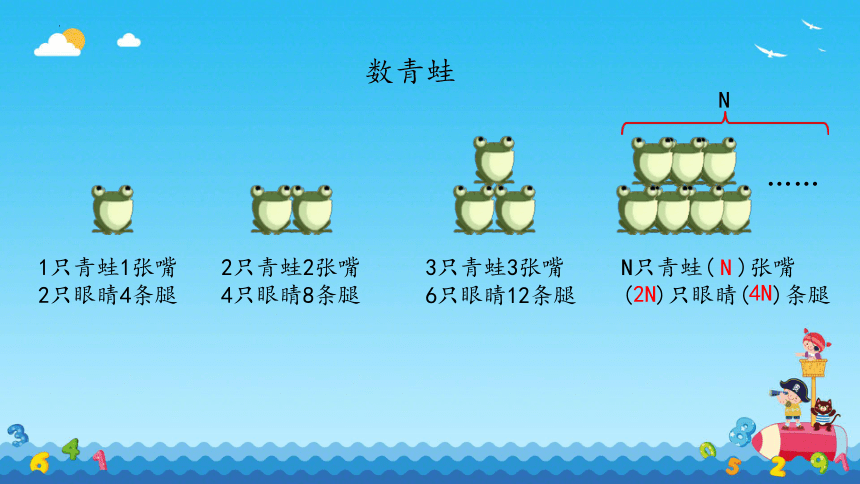
1只青蛙1张嘴
2只眼睛4条腿
数青蛙
2只青蛙2张嘴
4只眼睛8条腿
3只青蛙3张嘴
6只眼睛12条腿
N只青蛙( )张嘴
( )只眼睛( )条腿
……
N
N
4N
2N
a和b可以分别表示哪些数?
例3:学校计划每月用a吨水,实际平均每月 节约b吨水。
用洗过手的水喷洒教室吧!
怎样节约用水?
因为时学校用水,所以a和b都不能为0;
b表示平均每个月节约的水量,所以a>b。
(1)a-b:
(2)3a:
(3)3b:
(4)12(a-b):
表示实际每月用水的吨数。
表示3个月(一个季度)计划用水的吨数。
表示一个季度平均节约用水的吨数。
表示一年(12个月)实际用水的吨数。
说一说下面的式子表示什么意思。
理解含有字母的式子的含义时:要先理解式子中每个字母表示什么,不同的情景中,字母的取值范围也有所不同。
学校计划每月用a吨水,
实际平均每月节约b吨水。
例4:用字母表示正方形的面积公式和周长公式。
a
字母a
表示什么?
字母a
表示边长
正方形的周长=边长×4
C
a
=
×4
C=4a
正方形的面积=边长×边长
S
=
×
S=a2
a2
读作:a的平方
a
a
1.用含有字母的式子表示长方形的周长和面积。
a
b
长方形的面积=长×宽
长方形的周长=(长+宽)×2
C=_______
S=_______
C
=
×2
(a+b)
C=(a+b)×2
S
a
b
=
×
S=ab
2(a+b)
ab
(长)
(宽)
=2×(a+b)
=2(a+b)
C
2(a+b)
ab
3x
200-3x
3.用字母表示加法运算定律
例5:(1)不计算,在圈里填上合适的符号。
78+301
301+78
219+86
86+219
说一说你是怎么想的。
(2)用 、 表示任意两个数,在圈里应该填什么符号?
+
+
交换两个加数的位置,
和不变。
这叫做加法交换律。
=
=
=
(3)如果a表示一个加数,b表示另一个加数,加法 交换律可以用字母公式表示为:
a+b=b+a
加法交换律:交换两个加数的位置,和不变。
例6:计算下面两组题。
(1)
(18+49)+43
18+(49+43)
(2)
(125+68)+32
125+(68+32)
通过计算,你发现了什么?
=67
+43
=110
=18
+92
=110
=193
=125
=225
=225
+32
+100
这叫做加法结合律。
三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
如果a、b、c分别表示三个加数,加法结合律可以用字母公式表示为:
(a+b)+c=a+(b+c)
应用加法运算定律,可以进行简便运算。
(1) 27+34+66
(2) 75+39+125
加法结合律
=27
=127
+100
=75+125+39
=200+39
=239
加法交换律
=27+(34+66)
1.用简便方法计算。
336+245+264
139+256+161+244
189+425+275
312+188+247+153
=336+264+245
=600+245
=845
凑整
凑整
=(139+161)+(256+244)
=300+500
=800
=(312+188)+(247+153)
=500+400
=900
=189+(425+275)
=189+700
=889
加法交换律
凑整
770
720
680
540
420
800-n
80-x
15
35
320-102
320-218
c-b
c-a
和同近积大
a=50,b=50的时候积最大。
a=1,b=99或a=99,b=1的时候积最小。
第二单元 用字母表示数
1.用字母表示数量关系
麦当劳
停车场
妞妞
丫丫
我比妞妞大3岁
a
23+3=26
a+3
1+3=4
2+3=5
3+3=6
18+3=21
1
2
3
…
…
4
妞妞a岁时,丫丫就(a+3)岁了。
18
4+3=7
根据妞妞和丫丫的年龄关系,只要知道妞妞的年龄就能算出丫丫的年龄。
23
25+3=28
25
a=500?
例2:用含有字母的式子表示买 铅笔盒的钱数。
买3个铅笔盒需要( )元;
买5个铅笔盒需要( )元;
买18个铅笔盒需要( )元;
买a个铅笔盒需要( )元;
3×9=27
5×9=45
18×9=162
9×a
省略乘号时,一般把数写在字母的前面
x+y
2x+2y
3x+y
52+x
56
420
1176
28x
1764
104+x
9+x
2x+9
35x
20y
105x+60y
2.用字母表示公式
1只青蛙1张嘴
2只眼睛4条腿
数青蛙
2只青蛙2张嘴
4只眼睛8条腿
3只青蛙3张嘴
6只眼睛12条腿
N只青蛙( )张嘴
( )只眼睛( )条腿
……
N
N
4N
2N
a和b可以分别表示哪些数?
例3:学校计划每月用a吨水,实际平均每月 节约b吨水。
用洗过手的水喷洒教室吧!
怎样节约用水?
因为时学校用水,所以a和b都不能为0;
b表示平均每个月节约的水量,所以a>b。
(1)a-b:
(2)3a:
(3)3b:
(4)12(a-b):
表示实际每月用水的吨数。
表示3个月(一个季度)计划用水的吨数。
表示一个季度平均节约用水的吨数。
表示一年(12个月)实际用水的吨数。
说一说下面的式子表示什么意思。
理解含有字母的式子的含义时:要先理解式子中每个字母表示什么,不同的情景中,字母的取值范围也有所不同。
学校计划每月用a吨水,
实际平均每月节约b吨水。
例4:用字母表示正方形的面积公式和周长公式。
a
字母a
表示什么?
字母a
表示边长
正方形的周长=边长×4
C
a
=
×4
C=4a
正方形的面积=边长×边长
S
=
×
S=a2
a2
读作:a的平方
a
a
1.用含有字母的式子表示长方形的周长和面积。
a
b
长方形的面积=长×宽
长方形的周长=(长+宽)×2
C=_______
S=_______
C
=
×2
(a+b)
C=(a+b)×2
S
a
b
=
×
S=ab
2(a+b)
ab
(长)
(宽)
=2×(a+b)
=2(a+b)
C
2(a+b)
ab
3x
200-3x
3.用字母表示加法运算定律
例5:(1)不计算,在圈里填上合适的符号。
78+301
301+78
219+86
86+219
说一说你是怎么想的。
(2)用 、 表示任意两个数,在圈里应该填什么符号?
+
+
交换两个加数的位置,
和不变。
这叫做加法交换律。
=
=
=
(3)如果a表示一个加数,b表示另一个加数,加法 交换律可以用字母公式表示为:
a+b=b+a
加法交换律:交换两个加数的位置,和不变。
例6:计算下面两组题。
(1)
(18+49)+43
18+(49+43)
(2)
(125+68)+32
125+(68+32)
通过计算,你发现了什么?
=67
+43
=110
=18
+92
=110
=193
=125
=225
=225
+32
+100
这叫做加法结合律。
三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
如果a、b、c分别表示三个加数,加法结合律可以用字母公式表示为:
(a+b)+c=a+(b+c)
应用加法运算定律,可以进行简便运算。
(1) 27+34+66
(2) 75+39+125
加法结合律
=27
=127
+100
=75+125+39
=200+39
=239
加法交换律
=27+(34+66)
1.用简便方法计算。
336+245+264
139+256+161+244
189+425+275
312+188+247+153
=336+264+245
=600+245
=845
凑整
凑整
=(139+161)+(256+244)
=300+500
=800
=(312+188)+(247+153)
=500+400
=900
=189+(425+275)
=189+700
=889
加法交换律
凑整
770
720
680
540
420
800-n
80-x
15
35
320-102
320-218
c-b
c-a
和同近积大
a=50,b=50的时候积最大。
a=1,b=99或a=99,b=1的时候积最小。
