数学:第2章《数列》教案(苏教版必修5)
文档属性
| 名称 | 数学:第2章《数列》教案(苏教版必修5) |
|
|
| 格式 | rar | ||
| 文件大小 | 74.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
本章复习与小结(1)
【三维目标】:
1.系统掌握数列的有关概念和公式。
2.了解数列的通项公式与前n项和公式的关系。
3.能通过前项和公式求出数列的通项公式。
【授课类型】:复习课
【课时安排】:1课时
【教学思路】:
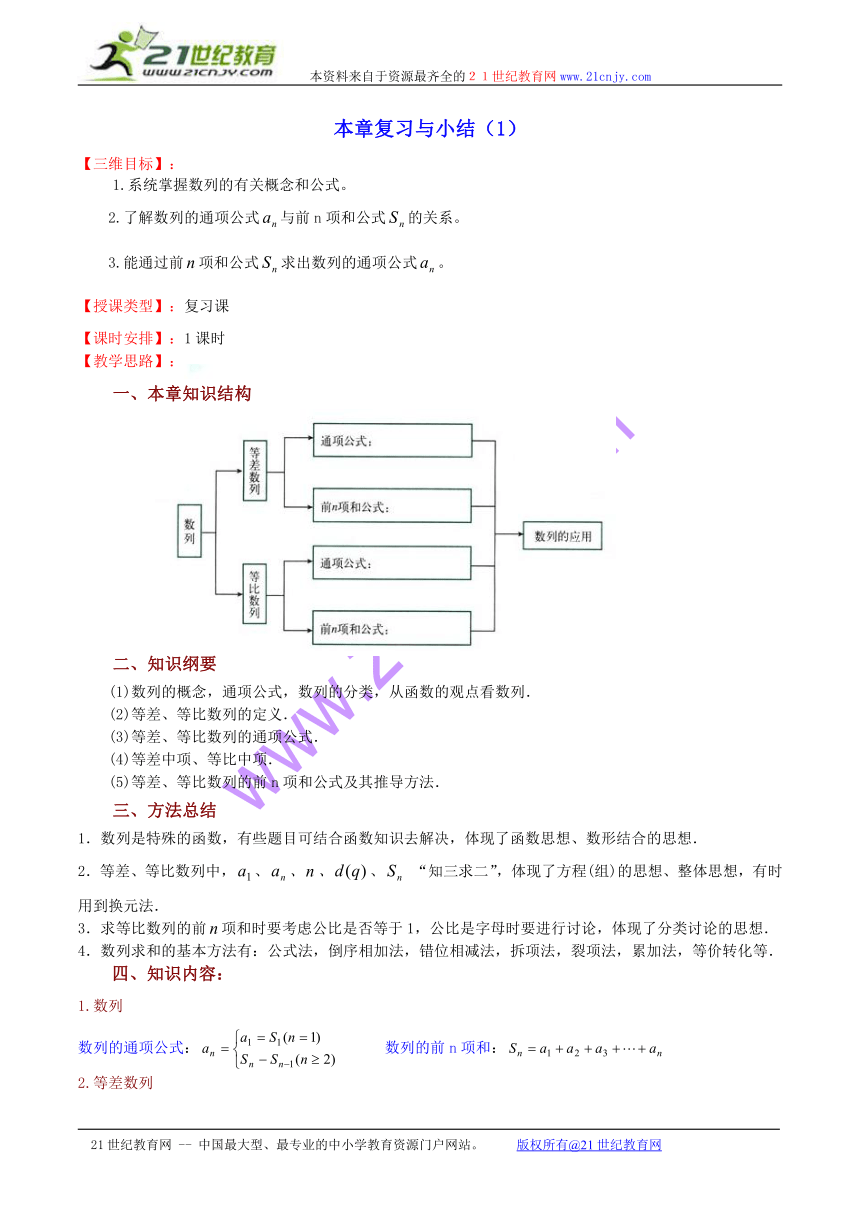
一、本章知识结构
二、知识纲要
(1)数列的概念,通项公式,数列的分类,从函数的观点看数列.
(2)等差、等比数列的定义.
(3)等差、等比数列的通项公式.
(4)等差中项、等比中项.
(5)等差、等比数列的前n项和公式及其推导方法.
三、方法总结
1.数列是特殊的函数,有些题目可结合函数知识去解决,体现了函数思想、数形结合的思想.
2.等差、等比数列中,、、、、 “知三求二”,体现了方程(组)的思想、整体思想,有时用到换元法.
3.求等比数列的前项和时要考虑公比是否等于1,公比是字母时要进行讨论,体现了分类讨论的思想.
4.数列求和的基本方法有:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等.
四、知识内容:
1.数列
数列的通项公式: 数列的前n项和:
2.等差数列
等差数列的定义:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母表示。
等差数列的判定方法:
(1)定义法:对于数列,若(常数),则数列是等差数列。
(2)等差中项:对于数列,若,则数列是等差数列。
等差数列的通项公式:
如果等差数列的首项是,公差是,则等差数列的通项为。
说明:该公式整理后是关于的一次函数。
等差数列的前项和:① ②
说明:对于公式②整理后是关于的没有常数项的二次函数。
等差中项:
如果,,成等差数列,那么叫做与的等差中项。即:或
说明:在一个等差数列中,从第2项起,每一项(有穷等差数列的末项除外)都是它的前一项与后一项的等差中项;事实上等差数列中某一项是与其等距离的前后两项的等差中项。
等差数列的性质:
(1)等差数列任意两项间的关系:如果是等差数列的第项,是等差数列的第项,且,公差为,则有
(2)对于等差数列,若,则。
也就是:,如图所示:
(3)若数列是等差数列,是其前n项的和,,那么,,成等差数列。如下图所示:
3.等比数列
等比数列的概念:
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示()。
等比中项:
如果在与之间插入一个数,使,,成等比数列,那么叫做与的等比中项。
也就是,如果是的等比中项,那么,即。
等比数列的判定方法:
(1)定义法:对于数列,若,则数列是等比数列。
(2)等比中项:对于数列,若,则数列是等比数列。
等比数列的通项公式:
如果等比数列的首项是,公比是,则等比数列的通项为。
等比数列的前n项和:
当时,
等比数列的性质:
①等比数列任意两项间的关系:如果是等比数列的第项,是等差数列的第项,且,公比为,则有
②对于等比数列,若,则
也就是:。如图所示:
③若数列是等比数列,是其前n项的和,,那么,,成等比数列。如下图所示:
4.数列前n项和
(1)重要公式:
;
;
(2)等差数列中,
(3)等比数列中,
(4)裂项求和:;()
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
本章复习与小结(1)
【三维目标】:
1.系统掌握数列的有关概念和公式。
2.了解数列的通项公式与前n项和公式的关系。
3.能通过前项和公式求出数列的通项公式。
【授课类型】:复习课
【课时安排】:1课时
【教学思路】:
一、本章知识结构
二、知识纲要
(1)数列的概念,通项公式,数列的分类,从函数的观点看数列.
(2)等差、等比数列的定义.
(3)等差、等比数列的通项公式.
(4)等差中项、等比中项.
(5)等差、等比数列的前n项和公式及其推导方法.
三、方法总结
1.数列是特殊的函数,有些题目可结合函数知识去解决,体现了函数思想、数形结合的思想.
2.等差、等比数列中,、、、、 “知三求二”,体现了方程(组)的思想、整体思想,有时用到换元法.
3.求等比数列的前项和时要考虑公比是否等于1,公比是字母时要进行讨论,体现了分类讨论的思想.
4.数列求和的基本方法有:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等.
四、知识内容:
1.数列
数列的通项公式: 数列的前n项和:
2.等差数列
等差数列的定义:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母表示。
等差数列的判定方法:
(1)定义法:对于数列,若(常数),则数列是等差数列。
(2)等差中项:对于数列,若,则数列是等差数列。
等差数列的通项公式:
如果等差数列的首项是,公差是,则等差数列的通项为。
说明:该公式整理后是关于的一次函数。
等差数列的前项和:① ②
说明:对于公式②整理后是关于的没有常数项的二次函数。
等差中项:
如果,,成等差数列,那么叫做与的等差中项。即:或
说明:在一个等差数列中,从第2项起,每一项(有穷等差数列的末项除外)都是它的前一项与后一项的等差中项;事实上等差数列中某一项是与其等距离的前后两项的等差中项。
等差数列的性质:
(1)等差数列任意两项间的关系:如果是等差数列的第项,是等差数列的第项,且,公差为,则有
(2)对于等差数列,若,则。
也就是:,如图所示:
(3)若数列是等差数列,是其前n项的和,,那么,,成等差数列。如下图所示:
3.等比数列
等比数列的概念:
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示()。
等比中项:
如果在与之间插入一个数,使,,成等比数列,那么叫做与的等比中项。
也就是,如果是的等比中项,那么,即。
等比数列的判定方法:
(1)定义法:对于数列,若,则数列是等比数列。
(2)等比中项:对于数列,若,则数列是等比数列。
等比数列的通项公式:
如果等比数列的首项是,公比是,则等比数列的通项为。
等比数列的前n项和:
当时,
等比数列的性质:
①等比数列任意两项间的关系:如果是等比数列的第项,是等差数列的第项,且,公比为,则有
②对于等比数列,若,则
也就是:。如图所示:
③若数列是等比数列,是其前n项的和,,那么,,成等比数列。如下图所示:
4.数列前n项和
(1)重要公式:
;
;
(2)等差数列中,
(3)等比数列中,
(4)裂项求和:;()
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
