数学:1.1.2《弧度制》教案(苏教版必修4)
文档属性
| 名称 | 数学:1.1.2《弧度制》教案(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第 2 课时:§1.1.2 弧度制
【三维目标】:
一、知识与技能
1.使学生理解弧度的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数
2.了解角的集合与实数集之间可以建立起一一对应关系。
3.掌握弧度制下的弧长公式,会利用弧度制解决某些简单的实际问题;
二、过程与方法
1.通过单位圆中的圆心角引入弧度的概念,比较两种度量角的方法探究角度制与弧度制之间的互化;应用在特殊角的角度制与弧度制的互化,帮助学生理解掌握;
2.以针对性的例题和习题使学生掌握弧长公式和扇形的面积公式;以具体的实例学习角度制与弧度制的互化,能正确使用计算器.
3.通过自主学习和合作学习,树立学生正确的学习态度。
三、情感、态度与价值观
1. 通过弧度制的学习,使学生理解并认识到角度制与弧度制都是度量角制度,二者虽单位不同,但是互相联系的、辩证统一的,进一步加强对辩证统一思想的理解;
2.在弧度制下,角的加、减运算可以像十进制一样进行,而不需要进行角度制与十进制之间的互化,化简了六十进制给角的加、减运算带来的诸多不便,体现了弧度制的简捷美;
3.通过弧度制与角度制的比较,使学生认识到引入弧度制的优越性,激发学生的学习兴趣和求知欲望,养成良好的学习品质。
4.教师可以向学生介绍或让学生查阅弧度制的历史和有关欧拉的资料,这有助于激发学生学习数学的兴趣和积极性。欧拉的有关事迹有助于陶冶学生情操,培养学生坚韧不拔的意志、实事求是的科学态度和勇于创新精神。
【教学重点与难点】:
重点:理解弧度制的意义,正确进行弧度与角度的换算;弧长和面积公式及应用。
难点:弧度的概念
关键:弄清1弧度的角的含义是建立弧度概念的关键
【学法与教学用具】:
1. 学法:在我们所掌握的知识中,知道角的度量是用角度制,但是为了以后的学习,我们引入了弧度制的概念,我们一定要准确理解弧度制的定义,在理解定义的基础上熟练掌握角度制与弧度制的互化. 在学习中,通过自主学习的形式,让学生感受弧度制的优越性,在类比中理解掌握弧度制。
在初中,我们非常熟悉角度制表示角,但在进行角的运算时,运用六十进制出现了很不习惯的问题,与我们常用的十进制不一样,正因为这样,所以有必要引入弧度制;
2. 教学用具:计算器、多媒体、实物投影仪、三角板.
【教学方法】:
通过几何画板多媒体课件的演示,给学生以直观的形象,使学生进一步理解弧度作为角的度量单位的可靠性和可行性。从特殊到一般,是人类认识事物的一般规律,让学生从某一个简单的、特殊的情况开始着手,更利于教学的开展和学生思维的拓展,共同找出弧度与角度换算的方法。通过设置问题启发引导学生观察、分析、归纳,使学生在独立思考的基础上更好地进行合作交流。
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
在初中几何里,我们学习过角的度量,1°的角是怎样定义的呢 (周角的为1°的角)
这种用度作为单位来度量角的单位制叫做角度制,但在数学和其他科学中我们还经常用到另一种度量角的单位制——弧度制。下面我们就来学习弧度制的有关概念.(板书课题)弧度制的单位是rad,读作弧度.
二、研探新知
长度等于半径的圆弧所对的圆心角称为1弧度的角,记作1 。用弧度作为角的单位来度量角的单位制称为弧度制(radian measure)。
正角的弧度数是正数,负角的弧度数是负数,零角的弧度数为0。若圆的半径为,圆心角所对的圆弧长为,则其弧度数就是;若半径为,圆心角所对的圆的弧长为,则其弧度数就是,故有
度
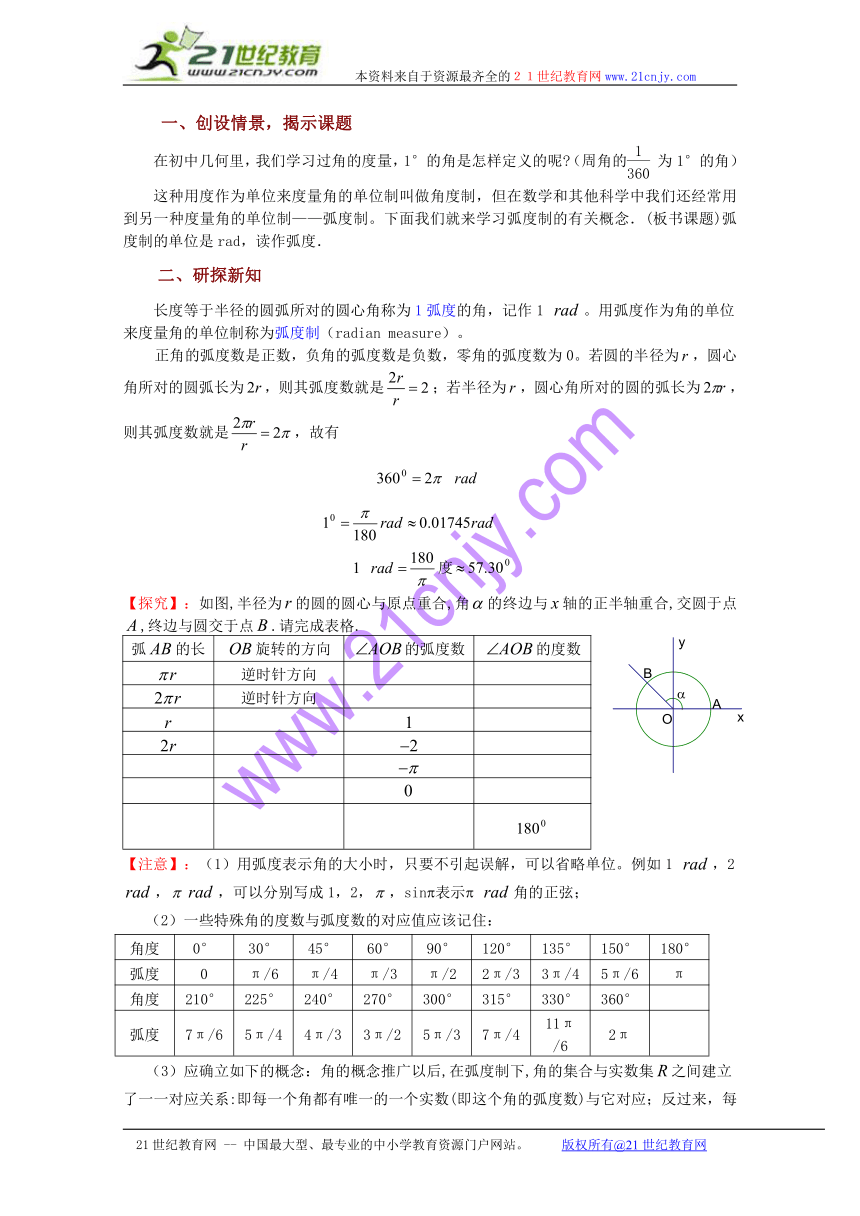
【探究】:如图,半径为的圆的圆心与原点重合,角的终边与轴的正半轴重合,交圆于点,终边与圆交于点.请完成表格.
弧的长 旋转的方向 的弧度数 的度数
逆时针方向
逆时针方向
【注意】:(1)用弧度表示角的大小时,只要不引起误解,可以省略单位。例如1 ,2 ,,可以分别写成1,2,,sin表示 角的正弦;
(2)一些特殊角的度数与弧度数的对应值应该记住:
角度 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π
角度 210° 225° 240° 270° 300° 315° 330° 360°
弧度 7π/6 5π/4 4π/3 3π/2 5π/3 7π/4 11π/6 2π
(3)应确立如下的概念:角的概念推广以后,在弧度制下,角的集合与实数集之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
任意角的集合 实数集R
弧长公式:
由公式: (比公式简单)
弧长等于弧所对的圆心角(的弧度数)的绝对值与半径的积
扇形面积公式: 其中是扇形弧长,是圆的半径。
(.这比扇形面积公式 要简单)
说明:①弧度制下的公式要显得简洁的多了;②以上公式中的必须为弧度单位.
三、质疑答辩,排难解惑,发展思维
例1(教材例1)把下列各角从弧度化为度:(1) (2)
解:(1) (2)
【举一反三】
1.将化为角度制是_____,5是第____象限角。
2.若为第四象限角,则为第____象限角
3.有以下四组角:①;②;③;④,,其中终边相同的是( ) .①和② .①、②和③ .①、②和④ .①、②、③和④
例2(教材例1)把下列各角从度化为弧度:(1);(2)
【举一反三】
1.将化为弧度制是____
2.比较大小:3_____, _____
3.集合,,则( )
. . . .
【触类旁通】
1. 在同一直角坐标系中用阴影画出集合:,
,并写出和
2.已知集合,,试求
例3 (教材例3)已知扇形的周长为8,圆心角为2,求该扇形的面积。
解:设扇形的半径为,弧长为,则有,解得,故扇形的面积为
【举一反三】
1.地球的赤道半径为6370千米,则赤道上1度的圆心角所对的弧长是_____,1弧度的圆心角所对的弧长是_____
2.若1弧度的圆心角所对的弧长为2,则此圆心角所夹的扇形的面积等于_____
3.一个半径为的扇形,若它的周长等于弧所在的半圆的长,那么扇形的圆心角是多少弧度?扇形的面积是多少?
例4 已知一扇形的周长为c(c>0),当扇形的弧长为何值时,它有最大面积?并求出面积的最大值.
【举一反三】
现有一根长为的铁丝,学生甲用它围成一个面积最大的矩形,学生乙用它围成一个面积最大的扇形,则两人围成的图形中,哪个面积较大?试说明理由。
四、巩固深化,反馈矫正
1.把45°化成弧度。解:45°=×45rad=rad.
2.把rad化成度。解:rad=×180°=108°.
3.将下列各角化成2k+(k的形式。(1); (2)
4.写出阴影部分的角的集合:
5.圆的半径变为原来的,而弧长不变,则该弧所对的圆心角是原来的 倍。
6.已知扇形的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
7.若2弧度的圆心角所对的弧长是,则这个圆心角所在的扇形面积是 .
五、归纳整理,整体认识
1.本节主要学习了弧度制的定义;弧度制与角度制的区别,角度与弧度的换算公式,使角的集合与实数集之间建立起一一对应关系;特殊角的弧度数;弧度制下的弧长公式、扇形面积公式
2.在本节课的学习过程中,还有那些不太明白的地方,请向老师提出。
六、承上启下,留下悬念
1.时钟的分针经过40分钟时间旋转的角度是______
2.把化成的形式是______
3.集合和关系是( )
(A) (B) (C) (D)
4.集合的关系是( )
(A) (B) (C) (D)以上都不对。
5.已知集合,则等于( )
(A) (B) (C) (D)或
6.下列各对角中终边相同的角是( )
A.(k∈Z) B. -和π C.-和 D.
7.设,则的取值范围是_______
8.将下列各角化成的形式,并确定其所在的象限
(1);(2)
9.已知集合,试求,,试求
10.一个扇形周长等于它的弧所在圆的周长的一半,若圆的半径为,求扇形的面积。
11.2弧度的圆心角所对的弦长为2,求这个圆心角所对的弧长,及圆心角所夹扇形面积(要求作图)。
12.已知扇形的周长为30,当它的半径和圆心角各取多少值时,扇形面积最大,最大值为多少?
13.(1)已知扇形的圆心角为,半径,求弧长及扇形面积。
(2)已知扇形周长为,当扇形的中心角为多大时它有最大面积,最大面积是多少?
预习提纲:锐角三角函数是用边的比来定义的,任意角的三角函数是怎样定义的
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
正角
零角
负角
正实数
零
负实数
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第 2 课时:§1.1.2 弧度制
【三维目标】:
一、知识与技能
1.使学生理解弧度的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数
2.了解角的集合与实数集之间可以建立起一一对应关系。
3.掌握弧度制下的弧长公式,会利用弧度制解决某些简单的实际问题;
二、过程与方法
1.通过单位圆中的圆心角引入弧度的概念,比较两种度量角的方法探究角度制与弧度制之间的互化;应用在特殊角的角度制与弧度制的互化,帮助学生理解掌握;
2.以针对性的例题和习题使学生掌握弧长公式和扇形的面积公式;以具体的实例学习角度制与弧度制的互化,能正确使用计算器.
3.通过自主学习和合作学习,树立学生正确的学习态度。
三、情感、态度与价值观
1. 通过弧度制的学习,使学生理解并认识到角度制与弧度制都是度量角制度,二者虽单位不同,但是互相联系的、辩证统一的,进一步加强对辩证统一思想的理解;
2.在弧度制下,角的加、减运算可以像十进制一样进行,而不需要进行角度制与十进制之间的互化,化简了六十进制给角的加、减运算带来的诸多不便,体现了弧度制的简捷美;
3.通过弧度制与角度制的比较,使学生认识到引入弧度制的优越性,激发学生的学习兴趣和求知欲望,养成良好的学习品质。
4.教师可以向学生介绍或让学生查阅弧度制的历史和有关欧拉的资料,这有助于激发学生学习数学的兴趣和积极性。欧拉的有关事迹有助于陶冶学生情操,培养学生坚韧不拔的意志、实事求是的科学态度和勇于创新精神。
【教学重点与难点】:
重点:理解弧度制的意义,正确进行弧度与角度的换算;弧长和面积公式及应用。
难点:弧度的概念
关键:弄清1弧度的角的含义是建立弧度概念的关键
【学法与教学用具】:
1. 学法:在我们所掌握的知识中,知道角的度量是用角度制,但是为了以后的学习,我们引入了弧度制的概念,我们一定要准确理解弧度制的定义,在理解定义的基础上熟练掌握角度制与弧度制的互化. 在学习中,通过自主学习的形式,让学生感受弧度制的优越性,在类比中理解掌握弧度制。
在初中,我们非常熟悉角度制表示角,但在进行角的运算时,运用六十进制出现了很不习惯的问题,与我们常用的十进制不一样,正因为这样,所以有必要引入弧度制;
2. 教学用具:计算器、多媒体、实物投影仪、三角板.
【教学方法】:
通过几何画板多媒体课件的演示,给学生以直观的形象,使学生进一步理解弧度作为角的度量单位的可靠性和可行性。从特殊到一般,是人类认识事物的一般规律,让学生从某一个简单的、特殊的情况开始着手,更利于教学的开展和学生思维的拓展,共同找出弧度与角度换算的方法。通过设置问题启发引导学生观察、分析、归纳,使学生在独立思考的基础上更好地进行合作交流。
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
在初中几何里,我们学习过角的度量,1°的角是怎样定义的呢 (周角的为1°的角)
这种用度作为单位来度量角的单位制叫做角度制,但在数学和其他科学中我们还经常用到另一种度量角的单位制——弧度制。下面我们就来学习弧度制的有关概念.(板书课题)弧度制的单位是rad,读作弧度.
二、研探新知
长度等于半径的圆弧所对的圆心角称为1弧度的角,记作1 。用弧度作为角的单位来度量角的单位制称为弧度制(radian measure)。
正角的弧度数是正数,负角的弧度数是负数,零角的弧度数为0。若圆的半径为,圆心角所对的圆弧长为,则其弧度数就是;若半径为,圆心角所对的圆的弧长为,则其弧度数就是,故有
度
【探究】:如图,半径为的圆的圆心与原点重合,角的终边与轴的正半轴重合,交圆于点,终边与圆交于点.请完成表格.
弧的长 旋转的方向 的弧度数 的度数
逆时针方向
逆时针方向
【注意】:(1)用弧度表示角的大小时,只要不引起误解,可以省略单位。例如1 ,2 ,,可以分别写成1,2,,sin表示 角的正弦;
(2)一些特殊角的度数与弧度数的对应值应该记住:
角度 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π
角度 210° 225° 240° 270° 300° 315° 330° 360°
弧度 7π/6 5π/4 4π/3 3π/2 5π/3 7π/4 11π/6 2π
(3)应确立如下的概念:角的概念推广以后,在弧度制下,角的集合与实数集之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
任意角的集合 实数集R
弧长公式:
由公式: (比公式简单)
弧长等于弧所对的圆心角(的弧度数)的绝对值与半径的积
扇形面积公式: 其中是扇形弧长,是圆的半径。
(.这比扇形面积公式 要简单)
说明:①弧度制下的公式要显得简洁的多了;②以上公式中的必须为弧度单位.
三、质疑答辩,排难解惑,发展思维
例1(教材例1)把下列各角从弧度化为度:(1) (2)
解:(1) (2)
【举一反三】
1.将化为角度制是_____,5是第____象限角。
2.若为第四象限角,则为第____象限角
3.有以下四组角:①;②;③;④,,其中终边相同的是( ) .①和② .①、②和③ .①、②和④ .①、②、③和④
例2(教材例1)把下列各角从度化为弧度:(1);(2)
【举一反三】
1.将化为弧度制是____
2.比较大小:3_____, _____
3.集合,,则( )
. . . .
【触类旁通】
1. 在同一直角坐标系中用阴影画出集合:,
,并写出和
2.已知集合,,试求
例3 (教材例3)已知扇形的周长为8,圆心角为2,求该扇形的面积。
解:设扇形的半径为,弧长为,则有,解得,故扇形的面积为
【举一反三】
1.地球的赤道半径为6370千米,则赤道上1度的圆心角所对的弧长是_____,1弧度的圆心角所对的弧长是_____
2.若1弧度的圆心角所对的弧长为2,则此圆心角所夹的扇形的面积等于_____
3.一个半径为的扇形,若它的周长等于弧所在的半圆的长,那么扇形的圆心角是多少弧度?扇形的面积是多少?
例4 已知一扇形的周长为c(c>0),当扇形的弧长为何值时,它有最大面积?并求出面积的最大值.
【举一反三】
现有一根长为的铁丝,学生甲用它围成一个面积最大的矩形,学生乙用它围成一个面积最大的扇形,则两人围成的图形中,哪个面积较大?试说明理由。
四、巩固深化,反馈矫正
1.把45°化成弧度。解:45°=×45rad=rad.
2.把rad化成度。解:rad=×180°=108°.
3.将下列各角化成2k+(k的形式。(1); (2)
4.写出阴影部分的角的集合:
5.圆的半径变为原来的,而弧长不变,则该弧所对的圆心角是原来的 倍。
6.已知扇形的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
7.若2弧度的圆心角所对的弧长是,则这个圆心角所在的扇形面积是 .
五、归纳整理,整体认识
1.本节主要学习了弧度制的定义;弧度制与角度制的区别,角度与弧度的换算公式,使角的集合与实数集之间建立起一一对应关系;特殊角的弧度数;弧度制下的弧长公式、扇形面积公式
2.在本节课的学习过程中,还有那些不太明白的地方,请向老师提出。
六、承上启下,留下悬念
1.时钟的分针经过40分钟时间旋转的角度是______
2.把化成的形式是______
3.集合和关系是( )
(A) (B) (C) (D)
4.集合的关系是( )
(A) (B) (C) (D)以上都不对。
5.已知集合,则等于( )
(A) (B) (C) (D)或
6.下列各对角中终边相同的角是( )
A.(k∈Z) B. -和π C.-和 D.
7.设,则的取值范围是_______
8.将下列各角化成的形式,并确定其所在的象限
(1);(2)
9.已知集合,试求,,试求
10.一个扇形周长等于它的弧所在圆的周长的一半,若圆的半径为,求扇形的面积。
11.2弧度的圆心角所对的弦长为2,求这个圆心角所对的弧长,及圆心角所夹扇形面积(要求作图)。
12.已知扇形的周长为30,当它的半径和圆心角各取多少值时,扇形面积最大,最大值为多少?
13.(1)已知扇形的圆心角为,半径,求弧长及扇形面积。
(2)已知扇形周长为,当扇形的中心角为多大时它有最大面积,最大面积是多少?
预习提纲:锐角三角函数是用边的比来定义的,任意角的三角函数是怎样定义的
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
正角
零角
负角
正实数
零
负实数
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
