数学:1.2.1《任意角的三角函数(二)》教案(苏教版必修4)
文档属性
| 名称 | 数学:1.2.1《任意角的三角函数(二)》教案(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第 4 课时:§1.2.1 任意角的三角函数(二)
【三维目标】:
一、知识与技能
1. 会用角的正弦线、余弦线、正切线分别表示任意角的正弦、余弦、正切函数值
2.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义;
3.能利用三角函数线解决一些简单的三角函数问题(利用三角函数线比较两个同名三角函数值的大小及表示角的范围)。
二、过程与方法
1.借助几何画板让学生经历概念的形成过程,提高学生观察、发现、类比、猜想和实验探索的能力;
2.在论坛上开展研究性学习,让学生借助所学知识自己去发现新问题,并加以解决,提高学生抽象概括、分析归纳、数学表述等基本数学思维能力.
三、情感、态度与价值观
1. 激发学生对数学研究的热情,培养学生勇于发现、勇于探索、勇于创新的精神;通过学生之间、师生之间的交流合作,实现共同探究、教学相长的教学情境.
2.通过三角函数的几何表示,使学生进一步加深对数形结合思想的理解,培养良好的思维习惯,拓展思维空间
【教学重点、难点与关键】:
重点:三角函数线的作法及其简单应用(利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切函数值分别用它们的几何形式表示出来).
难点:正确地用三角函数线表示任意角的三角函数值
关键:掌握有向线段及其数量的概念是克服难点的关键
【学法与教学用具】:
1.教法选择:“设置问题,探索辨析,归纳应用,延伸拓展”——科研式教学.
2.学法指导:类比、联想,产生知识迁移;观察、实验,体验知识的形成过程;猜想、求证,达到知识的延展.
3.教学手段:本节课教学地点选在多媒体网络教室,学生利用几何画板软件探讨数学问题,做数学实验;借助网络论坛交流各自的观点,展示自己的才能.
4. 教学用具:多媒体、实物投影仪.
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
1. 前面我们学习了角的弧度制,角弧度数的绝对值,其中是以角作为圆心角时所对弧的长,r是圆的半径。特别地, 当r =1时,,此时的圆称为单位圆,这样就可以用单位圆中弧的长度表示所对圆心角弧度数的绝对值,那么能否用几何图形来表示任意角的正弦、余弦、正切函数值呢?这就是我们今天一起要研究的问题.
二、研探新知
1.基本概念
(1)单位圆:圆心在圆点,半径等于单位长的圆叫做单位圆。
(2)有向线段:带有方向的线段.
坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向。
方向:按书写顺序,前者为起点,后者为终点,由起点指向终点.
如:有向线段,为起点,为终点,由点指向点.
(动态演示)
数值:(只考虑在坐标轴上或与坐标轴平行的有向线段)
绝对值等于线段的长度,若方向与坐标轴同向,取正值;与坐标轴反向,取负值.如:
= 1,
= -1,
=
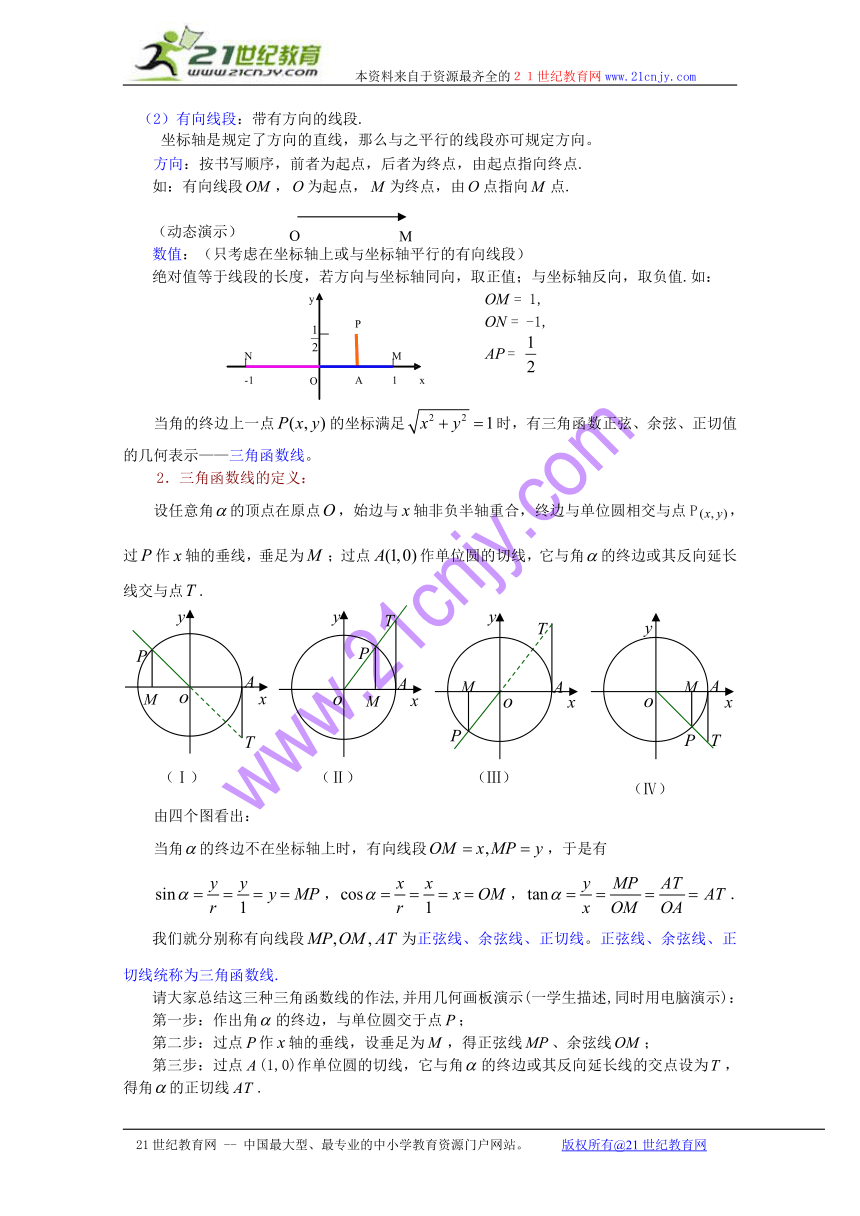
当角的终边上一点的坐标满足时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。
2.三角函数线的定义:
设任意角的顶点在原点,始边与轴非负半轴重合,终边与单位圆相交与点P,过作轴的垂线,垂足为;过点作单位圆的切线,它与角的终边或其反向延长线交与点.
由四个图看出:
当角的终边不在坐标轴上时,有向线段,于是有
,,.
我们就分别称有向线段为正弦线、余弦线、正切线。正弦线、余弦线、正切线统称为三角函数线.
请大家总结这三种三角函数线的作法,并用几何画板演示(一学生描述,同时用电脑演示):
第一步:作出角的终边,与单位圆交于点;
第二步:过点作轴的垂线,设垂足为,得正弦线、余弦线;
第三步:过点(1,0)作单位圆的切线,它与角的终边或其反向延长线的交点设为,得角的正切线.
特别注意:三角函数线是有向线段,在用字母表示这些线段时,要注意它们的方向,分清起点和终点,书写顺序不能颠倒.余弦线以原点为起点,正弦线和正切线以此线段与坐标轴的公共点为起点,其中点为定点(1,0).
【说明】:
①三条有向线段的位置:正弦线为的终边与单位圆的交点到轴的垂直线段;余弦线在轴上;正切线在过单位圆与轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
②三条有向线段的方向:正弦线由垂足指向的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与的终边的交点。
③三条有向线段的正负:三条有向线段凡与轴或轴同向的为正值,与轴或轴反向的为负值。
④三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。
三、质疑答辩,排难解惑,发展思维
例1.利用几何画板画出下列各角的正弦线、余弦线、正切线:
(1); (2); (3); (4).
学生先做,然后投影展示一学生的作品,并强调三角函数线的位置和方向.
例2.利用三角函数线比较下列各组数的大小:
(1)与 (2)tan与tan (3)cot与cot
解: 如图可知:
tan tan,cot cot
例3 利用几何画板画出适合下列条件的角的终边的范围,并由此写出角的集合:
(1) ; (2)≤- .
分析:先作出满足,的角的终边,然后根据已知条件确定角终边的范围.(几何画板动态演示)
答案:(1){}.
(2){}
【延伸】:通过(1)、(2)两图形的复合又可以得出不等式组的解集:
{}.
观察角的终边在各位置的情形,结合三角函数线和已学知识,你能发现什么规律,得出哪些结论?请说明你的观点和理由,并发表于教育论坛。
学生得出的结论有以下几种:
(1) sin2 + cos2 = 1;
(2)│sin│ + │cos │≥1;
(3) -1≤sin≤1, -1≤cos≤1, tan∈R;
(4) 若两角终边互为反向延长线,则两角的正切值相等,正弦、余弦值互为相反数;
(5) 当角的终边在第一象限逆时针旋转时,正弦、正切值逐渐增大,余弦值逐渐减小;
(6) 当角的终边在直线的右下方时, sin<cos;当角的终边在直线的左上方时, sin>cos。
【触类旁通】:利用三角函数线写符合下列条件的角的集合:(1) (2)
四、巩固深化,反馈矫正
1.利用三角函数线作出符合下列条件的角的终边,并写出这些角的集合:
(1) (2) (3)
2.利用三角函数线作出符合下列条件的角的终边,并写出这些角的集合:
(1) (2)
五、归纳整理,整体认识
1.三角函数线的定义;会画任意角的三角函数线
2.利用单位圆比较三角函数值的大小,求角的范围。
3.三角函数线的应用
六、承上启下,留下悬念
1.作出下列各角的正弦线、余弦线、正切线。
(1); (2); (3); (4); (5)-45°
2.利用单位圆写出符合下列条件的角的范围。
(1); (2); (3)tan (3);
(4)且; (5)且.
答案:(1);(2);
(3); (4);
(5).
3.类比正切线的作法,你能作出余切线吗?
4.结合三角函数线我们已经发现了一些很有价值的结论,你还能得出哪些结论?请大家继续在论坛上交流.
5.查阅数学家欧拉的生平事迹,了解他在数学方面的突出贡献,谈谈你的学习感受,并发表于论坛交流.
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
O
M
(Ⅳ)
(Ⅲ)
(Ⅱ)
(Ⅰ)
A
B
o
T2
T1
S2 S1
P2
P1
M2 M1 S1
x
y
o
P1
P2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第 4 课时:§1.2.1 任意角的三角函数(二)
【三维目标】:
一、知识与技能
1. 会用角的正弦线、余弦线、正切线分别表示任意角的正弦、余弦、正切函数值
2.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义;
3.能利用三角函数线解决一些简单的三角函数问题(利用三角函数线比较两个同名三角函数值的大小及表示角的范围)。
二、过程与方法
1.借助几何画板让学生经历概念的形成过程,提高学生观察、发现、类比、猜想和实验探索的能力;
2.在论坛上开展研究性学习,让学生借助所学知识自己去发现新问题,并加以解决,提高学生抽象概括、分析归纳、数学表述等基本数学思维能力.
三、情感、态度与价值观
1. 激发学生对数学研究的热情,培养学生勇于发现、勇于探索、勇于创新的精神;通过学生之间、师生之间的交流合作,实现共同探究、教学相长的教学情境.
2.通过三角函数的几何表示,使学生进一步加深对数形结合思想的理解,培养良好的思维习惯,拓展思维空间
【教学重点、难点与关键】:
重点:三角函数线的作法及其简单应用(利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切函数值分别用它们的几何形式表示出来).
难点:正确地用三角函数线表示任意角的三角函数值
关键:掌握有向线段及其数量的概念是克服难点的关键
【学法与教学用具】:
1.教法选择:“设置问题,探索辨析,归纳应用,延伸拓展”——科研式教学.
2.学法指导:类比、联想,产生知识迁移;观察、实验,体验知识的形成过程;猜想、求证,达到知识的延展.
3.教学手段:本节课教学地点选在多媒体网络教室,学生利用几何画板软件探讨数学问题,做数学实验;借助网络论坛交流各自的观点,展示自己的才能.
4. 教学用具:多媒体、实物投影仪.
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
1. 前面我们学习了角的弧度制,角弧度数的绝对值,其中是以角作为圆心角时所对弧的长,r是圆的半径。特别地, 当r =1时,,此时的圆称为单位圆,这样就可以用单位圆中弧的长度表示所对圆心角弧度数的绝对值,那么能否用几何图形来表示任意角的正弦、余弦、正切函数值呢?这就是我们今天一起要研究的问题.
二、研探新知
1.基本概念
(1)单位圆:圆心在圆点,半径等于单位长的圆叫做单位圆。
(2)有向线段:带有方向的线段.
坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向。
方向:按书写顺序,前者为起点,后者为终点,由起点指向终点.
如:有向线段,为起点,为终点,由点指向点.
(动态演示)
数值:(只考虑在坐标轴上或与坐标轴平行的有向线段)
绝对值等于线段的长度,若方向与坐标轴同向,取正值;与坐标轴反向,取负值.如:
= 1,
= -1,
=
当角的终边上一点的坐标满足时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。
2.三角函数线的定义:
设任意角的顶点在原点,始边与轴非负半轴重合,终边与单位圆相交与点P,过作轴的垂线,垂足为;过点作单位圆的切线,它与角的终边或其反向延长线交与点.
由四个图看出:
当角的终边不在坐标轴上时,有向线段,于是有
,,.
我们就分别称有向线段为正弦线、余弦线、正切线。正弦线、余弦线、正切线统称为三角函数线.
请大家总结这三种三角函数线的作法,并用几何画板演示(一学生描述,同时用电脑演示):
第一步:作出角的终边,与单位圆交于点;
第二步:过点作轴的垂线,设垂足为,得正弦线、余弦线;
第三步:过点(1,0)作单位圆的切线,它与角的终边或其反向延长线的交点设为,得角的正切线.
特别注意:三角函数线是有向线段,在用字母表示这些线段时,要注意它们的方向,分清起点和终点,书写顺序不能颠倒.余弦线以原点为起点,正弦线和正切线以此线段与坐标轴的公共点为起点,其中点为定点(1,0).
【说明】:
①三条有向线段的位置:正弦线为的终边与单位圆的交点到轴的垂直线段;余弦线在轴上;正切线在过单位圆与轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
②三条有向线段的方向:正弦线由垂足指向的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与的终边的交点。
③三条有向线段的正负:三条有向线段凡与轴或轴同向的为正值,与轴或轴反向的为负值。
④三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。
三、质疑答辩,排难解惑,发展思维
例1.利用几何画板画出下列各角的正弦线、余弦线、正切线:
(1); (2); (3); (4).
学生先做,然后投影展示一学生的作品,并强调三角函数线的位置和方向.
例2.利用三角函数线比较下列各组数的大小:
(1)与 (2)tan与tan (3)cot与cot
解: 如图可知:
tan tan,cot cot
例3 利用几何画板画出适合下列条件的角的终边的范围,并由此写出角的集合:
(1) ; (2)≤- .
分析:先作出满足,的角的终边,然后根据已知条件确定角终边的范围.(几何画板动态演示)
答案:(1){}.
(2){}
【延伸】:通过(1)、(2)两图形的复合又可以得出不等式组的解集:
{}.
观察角的终边在各位置的情形,结合三角函数线和已学知识,你能发现什么规律,得出哪些结论?请说明你的观点和理由,并发表于教育论坛。
学生得出的结论有以下几种:
(1) sin2 + cos2 = 1;
(2)│sin│ + │cos │≥1;
(3) -1≤sin≤1, -1≤cos≤1, tan∈R;
(4) 若两角终边互为反向延长线,则两角的正切值相等,正弦、余弦值互为相反数;
(5) 当角的终边在第一象限逆时针旋转时,正弦、正切值逐渐增大,余弦值逐渐减小;
(6) 当角的终边在直线的右下方时, sin<cos;当角的终边在直线的左上方时, sin>cos。
【触类旁通】:利用三角函数线写符合下列条件的角的集合:(1) (2)
四、巩固深化,反馈矫正
1.利用三角函数线作出符合下列条件的角的终边,并写出这些角的集合:
(1) (2) (3)
2.利用三角函数线作出符合下列条件的角的终边,并写出这些角的集合:
(1) (2)
五、归纳整理,整体认识
1.三角函数线的定义;会画任意角的三角函数线
2.利用单位圆比较三角函数值的大小,求角的范围。
3.三角函数线的应用
六、承上启下,留下悬念
1.作出下列各角的正弦线、余弦线、正切线。
(1); (2); (3); (4); (5)-45°
2.利用单位圆写出符合下列条件的角的范围。
(1); (2); (3)tan (3);
(4)且; (5)且.
答案:(1);(2);
(3); (4);
(5).
3.类比正切线的作法,你能作出余切线吗?
4.结合三角函数线我们已经发现了一些很有价值的结论,你还能得出哪些结论?请大家继续在论坛上交流.
5.查阅数学家欧拉的生平事迹,了解他在数学方面的突出贡献,谈谈你的学习感受,并发表于论坛交流.
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
O
M
(Ⅳ)
(Ⅲ)
(Ⅱ)
(Ⅰ)
A
B
o
T2
T1
S2 S1
P2
P1
M2 M1 S1
x
y
o
P1
P2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
