数学:1.2《余弦定理(1)》教案(苏教版必修5)
文档属性
| 名称 | 数学:1.2《余弦定理(1)》教案(苏教版必修5) |  | |
| 格式 | rar | ||
| 文件大小 | 45.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 08:02:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.2 30°,45°,60°角的三角函数值 同步练习
一、填空题: (4分×6=24分)
1.在Rt△ABC中,∠C=90°,∠A=30°,则sinB=______,tanA=_______.
2.计算: =____________.
3.已知,则锐角α的度数为_____;
若,则锐角α的度数为_____.
4.已知∠B是锐角,若,则tanB的值为_______.
5.式子1-2sin30°·cos30°的值为_________.
6.在△ABC中,若∠B=30°,tanC=2,AB=2,则BC=_______.
二、选择题: (4分×6=24分)
7.在△ABC中,∠C=90°,sinA=,则cosB的值为( )
A.1 B. C. D.
8.若tana=,且α为锐角,则cosα等于( )
A. B. C. D.
9.在△ABC中,∠C=90°,如果AB=2,BC=1,那么∠A的度数为( )
A.30° B.45° C.60° D.90°
10.在Rt△ABC中,∠C=90°,且tanA=,则sinB的值为( )
A. B. C. D.
11.在△ABC中,若,则∠C的度数为( )
A.30° B.60° C.90° D.120°
12.计算5sin30°+2cos245°-tan260°的值是( )
A. B. C.- D.1
三、解答题: (52分)
13.计算:
(1)tan60°·cos30°-3tan30°·tan45°;
(2)sin30°+cos60°-tan45°-tan30°·tan60°;
(3);
(4)cos60°-3tan30°+tan60°+2sin245°.
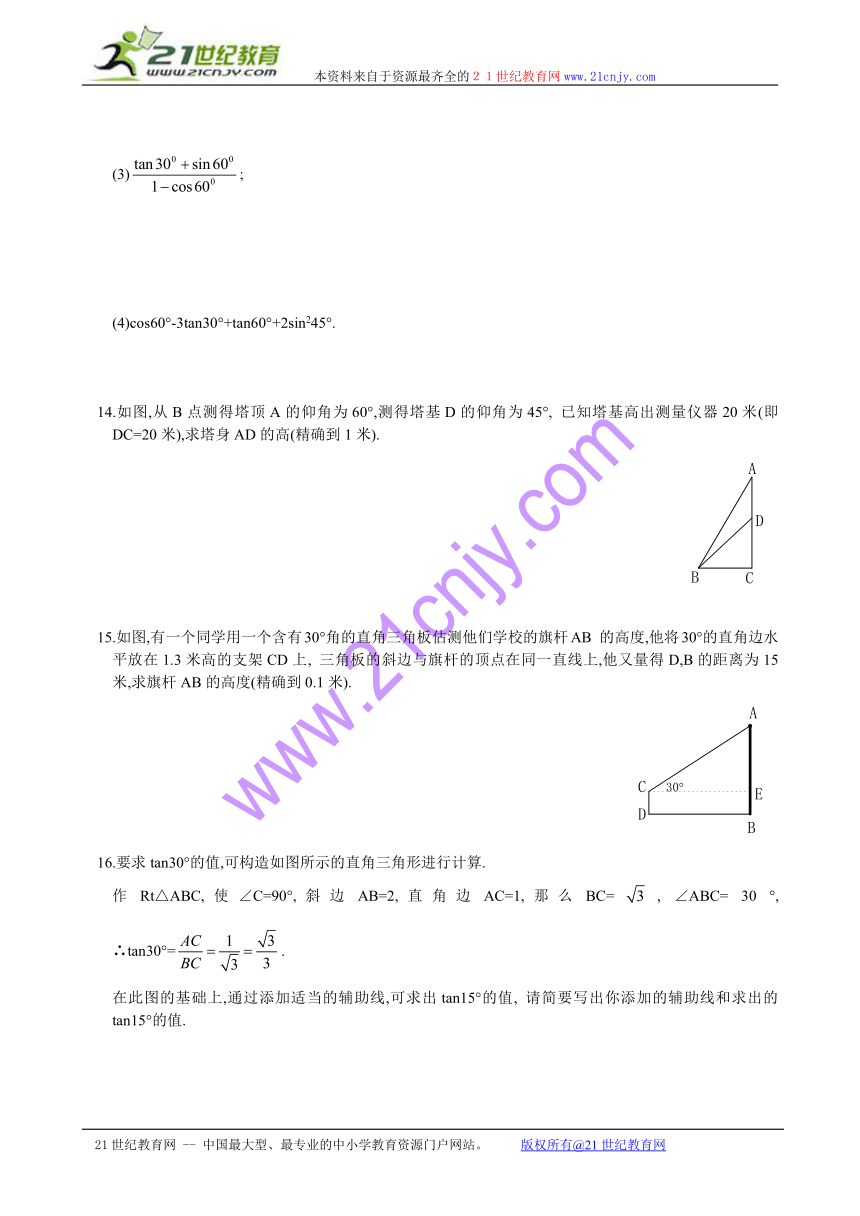
14.如图,从B点测得塔顶A的仰角为60°,测得塔基D的仰角为45°, 已知塔基高出测量仪器20米(即DC=20米),求塔身AD的高(精确到1米).
15.如图,有一个同学用一个含有30°角的直角三角板估测他们学校的旗杆AB 的高度,他将30°的直角边水平放在1.3米高的支架CD上, 三角板的斜边与旗杆的顶点在同一直线上,他又量得D,B的距离为15米,求旗杆AB的高度(精确到0.1米).
16.要求tan30°的值,可构造如图所示的直角三角形进行计算.
作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=, ∠ABC= 30 °, ∴tan30°=.
在此图的基础上,通过添加适当的辅助线,可求出tan15°的值, 请简要写出你添加的辅助线和求出的tan15°的值.
17.某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米)
18.如图,点A的坐标是(0.5,0),现在点A绕着点O按逆时针方向旋转, 每秒钟旋转30°,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11 秒钟时到达图中的P点处,求P点的坐标.
答案:
1. 2. 3.60°,30° 4. 5.1- 6. 7.B 8.A 9.A 10.A 11.D 12. B
13.(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
14.在Rt△BCD中,tan∠CBD=tan45°==1,故BC=DC=20米.
在Rt△ABC中,tan ∠ABC=tan60°=,
故AC=BCtan60°=米,从而AD=AC-CD=-20≈15米.
15.CE=BD=15米.在Rt△ACE中,∠ACE=30°,故tan30°=,AE=15×=5 (米), 故AB=AE+BE=5+1.3≈8.66+1.3=9.96≈10.0(米).
16.延长CB到D,使BD=BA,则∠D=∠DAB.又∠D+∠DAB=30°,故∠D=15°.
DC=BD+ BC=2+,
故tan15°=.
17.如图,由已知得∠AMB=90°,∠A=30°,MN=0.7千米.
在Rt△AMN中,∵∠A=30°,∠ANM=90°,MN=0.7千米.
∴AM=2MN=1.4(千米).
在Rt△AMB中,∵∠A=30°,∠AMB=90°,AM=1.4千米.
∴AB=≈1.6(千米)
即湖心亭A到游船码头B的距离约为1.6千米.
18.由已知得,点A到P时旋转了330°,故∠POx=30°,OP=0.5+11×0.5=6.过P作PB ⊥x轴于B,则在Rt△POB中,OB=OP.cos30°=3,PB=OP·sin30°=3.故P(3,-3)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.2 30°,45°,60°角的三角函数值 同步练习
一、填空题: (4分×6=24分)
1.在Rt△ABC中,∠C=90°,∠A=30°,则sinB=______,tanA=_______.
2.计算: =____________.
3.已知,则锐角α的度数为_____;
若,则锐角α的度数为_____.
4.已知∠B是锐角,若,则tanB的值为_______.
5.式子1-2sin30°·cos30°的值为_________.
6.在△ABC中,若∠B=30°,tanC=2,AB=2,则BC=_______.
二、选择题: (4分×6=24分)
7.在△ABC中,∠C=90°,sinA=,则cosB的值为( )
A.1 B. C. D.
8.若tana=,且α为锐角,则cosα等于( )
A. B. C. D.
9.在△ABC中,∠C=90°,如果AB=2,BC=1,那么∠A的度数为( )
A.30° B.45° C.60° D.90°
10.在Rt△ABC中,∠C=90°,且tanA=,则sinB的值为( )
A. B. C. D.
11.在△ABC中,若,则∠C的度数为( )
A.30° B.60° C.90° D.120°
12.计算5sin30°+2cos245°-tan260°的值是( )
A. B. C.- D.1
三、解答题: (52分)
13.计算:
(1)tan60°·cos30°-3tan30°·tan45°;
(2)sin30°+cos60°-tan45°-tan30°·tan60°;
(3);
(4)cos60°-3tan30°+tan60°+2sin245°.
14.如图,从B点测得塔顶A的仰角为60°,测得塔基D的仰角为45°, 已知塔基高出测量仪器20米(即DC=20米),求塔身AD的高(精确到1米).
15.如图,有一个同学用一个含有30°角的直角三角板估测他们学校的旗杆AB 的高度,他将30°的直角边水平放在1.3米高的支架CD上, 三角板的斜边与旗杆的顶点在同一直线上,他又量得D,B的距离为15米,求旗杆AB的高度(精确到0.1米).
16.要求tan30°的值,可构造如图所示的直角三角形进行计算.
作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=, ∠ABC= 30 °, ∴tan30°=.
在此图的基础上,通过添加适当的辅助线,可求出tan15°的值, 请简要写出你添加的辅助线和求出的tan15°的值.
17.某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米)
18.如图,点A的坐标是(0.5,0),现在点A绕着点O按逆时针方向旋转, 每秒钟旋转30°,同时点A离开O点的距离以每秒0.5个单位的速度在增大,当A点第11 秒钟时到达图中的P点处,求P点的坐标.
答案:
1. 2. 3.60°,30° 4. 5.1- 6. 7.B 8.A 9.A 10.A 11.D 12. B
13.(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
14.在Rt△BCD中,tan∠CBD=tan45°==1,故BC=DC=20米.
在Rt△ABC中,tan ∠ABC=tan60°=,
故AC=BCtan60°=米,从而AD=AC-CD=-20≈15米.
15.CE=BD=15米.在Rt△ACE中,∠ACE=30°,故tan30°=,AE=15×=5 (米), 故AB=AE+BE=5+1.3≈8.66+1.3=9.96≈10.0(米).
16.延长CB到D,使BD=BA,则∠D=∠DAB.又∠D+∠DAB=30°,故∠D=15°.
DC=BD+ BC=2+,
故tan15°=.
17.如图,由已知得∠AMB=90°,∠A=30°,MN=0.7千米.
在Rt△AMN中,∵∠A=30°,∠ANM=90°,MN=0.7千米.
∴AM=2MN=1.4(千米).
在Rt△AMB中,∵∠A=30°,∠AMB=90°,AM=1.4千米.
∴AB=≈1.6(千米)
即湖心亭A到游船码头B的距离约为1.6千米.
18.由已知得,点A到P时旋转了330°,故∠POx=30°,OP=0.5+11×0.5=6.过P作PB ⊥x轴于B,则在Rt△POB中,OB=OP.cos30°=3,PB=OP·sin30°=3.故P(3,-3)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
