数学:1.3.2《三角函数的图象和性质(三)》教案(苏教版必修4)
文档属性
| 名称 | 数学:1.3.2《三角函数的图象和性质(三)》教案(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 67.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第 11 课时:§1.3.2 三角函数的图象和性质(三)
【三维目标】:
一、知识与技能
1.借助正切线画出正切函数的图象,并通过图象理解正切函数的性质。
2.能够应用正切函数性质解决一些相关问题。
3.掌握用数形结合的思想理解和处理有关问题的技能;发现数学规律,提高数学素质,培养实践第一观点.
二、过程与方法
1.类比正、余弦函数的概念,引入正切函数的概念;让学生通过类比,联系正弦函数图像的作法,通过单位圆中的有向线段得到正切函数的图像;能学以致用,结合图像分析得到正切函数的诱导公式和正切函数的性质。
2.通过作图来认识三角函数性质,充分发挥图象在认识和研究函数性质中的作用,渗透“数形结合”的思想
三、情感、态度与价值观
1.会用联系的观点看问题,使学生理解动与静的辩证关系。
2.通过学生动手操作,激发学生学习数学的兴趣和积极性,陶冶学生的情操,培养学生坚忍不拔的意志、实事求是的科学学习态度和勇于创新的精神。
【教学重点与难点】:
重点:正切函数的图象和性质;
难点:正切函数的图象和性质
教学疑点:正切函数在每个单调区间是增函数,并非整个定义域内的增函数;
【学法与教学用具】:
1. 学法:通过单位圆中的正切线画出正切函数的图像,并从图像观察总结出正切函数的性质。
2. 教学用具:三角板、多媒体、实物投影仪.
3. 教学模式:启发、诱导发现教学、讲练结合
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
1.回忆正、余弦函数的性质:定义域、值域、周期性、奇偶性、单调性。
2.求出下列函数的最小正周期,并说明下列函数是否有最大值、最小值,如果有,请写出取最大值、最小值时的自变量的集合. (1);(2).
3. 提问:如何比较与的大小?
4. 提问:能否类比研究正弦、余弦函数性质的方法来研究正切函数的图象和性质?
5.练习画下切线(分四个象限)
二、研探新知
1.正切函数的定义域是什么?
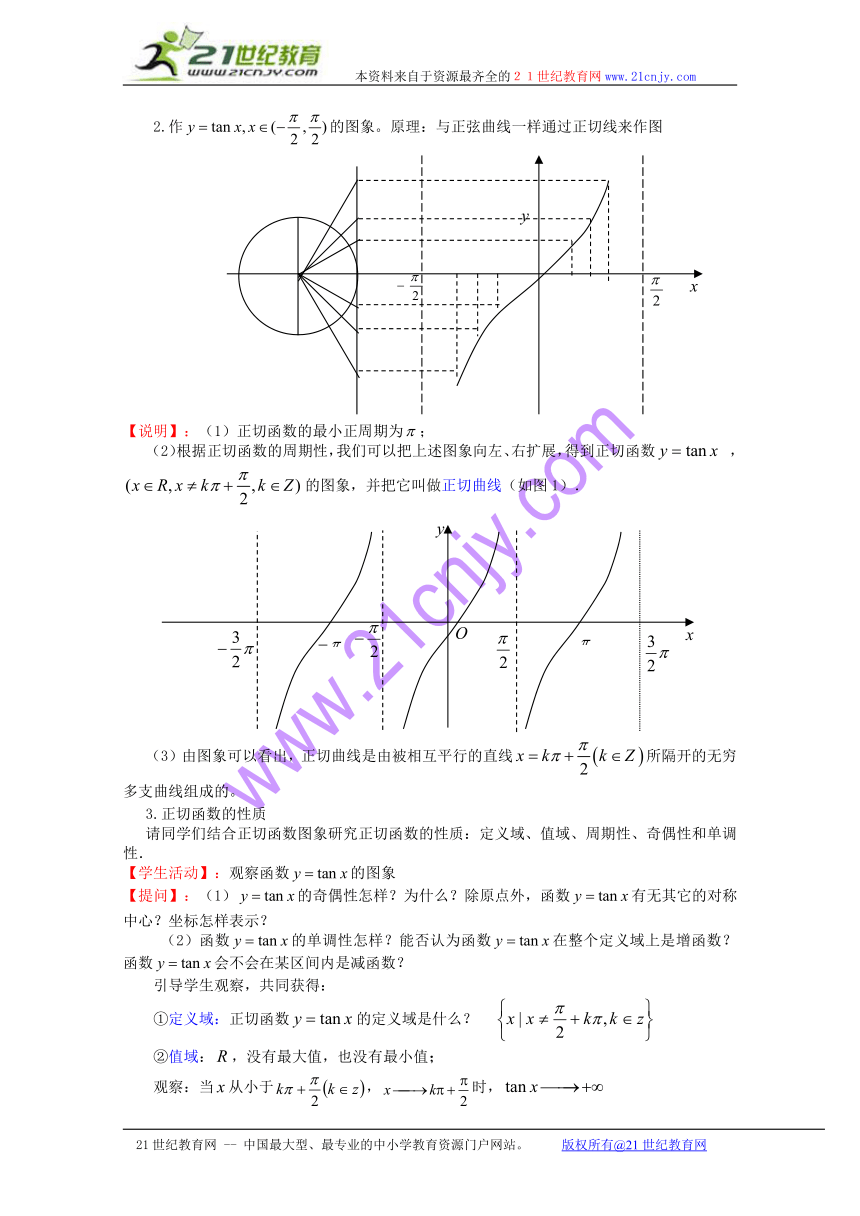
2.作的图象。原理:与正弦曲线一样通过正切线来作图
【说明】:(1)正切函数的最小正周期为;
(2)根据正切函数的周期性,我们可以把上述图象向左、右扩展,得到正切函数 ,的图象,并把它叫做正切曲线(如图1).
(3)由图象可以看出,正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的。
3.正切函数的性质
请同学们结合正切函数图象研究正切函数的性质:定义域、值域、周期性、奇偶性和单调性.
【学生活动】:观察函数的图象
【提问】:(1)的奇偶性怎样?为什么?除原点外,函数有无其它的对称中心?坐标怎样表示?
(2)函数的单调性怎样?能否认为函数在整个定义域上是增函数?函数会不会在某区间内是减函数?
引导学生观察,共同获得:
①定义域:正切函数的定义域是什么?
②值域:,没有最大值,也没有最小值;
观察:当从小于,时,
当从大于,时,。
③周期性:由诱导公式可知,正切函数是周期函数,最小正周期是.
④奇偶性:,∴正切函数是奇函数,正切曲线关于原点对称.
⑤单调性:由正切曲线图象可知:由正切线的变化规律可以看出,正切函数在内是增函数,又由正切函数的周期性可知,正切函数在开区间内都是增函数(在整个定义域内是增函数吗?)
⑥对称性:对称中心为(有对称轴吗 )
【强调】:a.不能说正切函数在整个定义域内是增函数
b.正切函数在每个单调区间内都是增函数
c.每个单调区间都包括两个象限:四、一或二、三
三、质疑答辩,排难解惑,发展思维
例1.(教材例4)求函数的定义域
例2.比较与的大小
例3.观察正切曲线写出满足下列条件的的值的范围:(1)(2)
例4.讨论函数的性质
四、巩固深化,反馈矫正
1.下列函数的单调增区间:(1)y=sin() (2) y=sin()
(3) (4) (5)
(6) (7) y=-cosx
【引申】:函数y=,在[ , ]是递 函数;
函数y=(cosx),在[ 0, ]是递 函数
2.(1)比较大小;
(2); (3)
3.判断下列函数的奇偶性
(1) y=sin(-2x) (2)f(x)=sin4x-cos4x+cos2x;
(3) (4)y=cosxlg(sinx+)
(5)f(x)=sin(2x+)
【引申】:已知(a、b为常数),且,求
4.(1)函数图象的对称轴是 ;对称中心是 .
(2)函数的对称轴是________;(3)的对称轴是________
(4)的对称中心为
(5)函数的图象的对称轴方程是_______
5. 求下列函数的最大值及取得最大值时自变量的集合:
(1);(2)
6. 求下列函数的最小正周期:(1) y=|sinx| (2)y=|sinx|+|cosx|
7. 根据正弦函数、余弦函数的图象,写出使下列不等式成立的x的集合
(1)sinx≥ (2)cosx≤- (3)2cosx-1>0
(1)sinx≥(x∈R) (2)+2cosx≥0 (x∈R)
五、归纳整理,整体认识
(1)这节课我们采用类比的思想方法来学习正切函数的图象和性质
(2)正切函数的作图是利用平移正切线得到的,当我们获得一个周期上图象后,再利用周期性把该段图象向左右延伸、平移。
因为正切函数的定义域是,所以它的图象被等相互平行的直线所隔开,而在相邻平行线间的图象是连续的。作出正切函数的图象,是先作出长度为一个周期(-π/2,π/2)的区间内的函数的图象,然后再将它沿轴向左或向右移动,每次移动的距离是π个单位,就可以得到整个正切函数的图象。
(3)正切函数的性质(周期的求法、奇偶性的判断、单调区间的求法)
讨论函数的单调性应借助图象或相关的函数的单调性;形如,≠ (k∈Z)的周期T=;注意正切函数的图象是由不连续的无数条曲线组成的
六、承上启下,留下悬念
预习函数y=Asin(ωx+φ)的图象
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
y
y
0
x
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第 11 课时:§1.3.2 三角函数的图象和性质(三)
【三维目标】:
一、知识与技能
1.借助正切线画出正切函数的图象,并通过图象理解正切函数的性质。
2.能够应用正切函数性质解决一些相关问题。
3.掌握用数形结合的思想理解和处理有关问题的技能;发现数学规律,提高数学素质,培养实践第一观点.
二、过程与方法
1.类比正、余弦函数的概念,引入正切函数的概念;让学生通过类比,联系正弦函数图像的作法,通过单位圆中的有向线段得到正切函数的图像;能学以致用,结合图像分析得到正切函数的诱导公式和正切函数的性质。
2.通过作图来认识三角函数性质,充分发挥图象在认识和研究函数性质中的作用,渗透“数形结合”的思想
三、情感、态度与价值观
1.会用联系的观点看问题,使学生理解动与静的辩证关系。
2.通过学生动手操作,激发学生学习数学的兴趣和积极性,陶冶学生的情操,培养学生坚忍不拔的意志、实事求是的科学学习态度和勇于创新的精神。
【教学重点与难点】:
重点:正切函数的图象和性质;
难点:正切函数的图象和性质
教学疑点:正切函数在每个单调区间是增函数,并非整个定义域内的增函数;
【学法与教学用具】:
1. 学法:通过单位圆中的正切线画出正切函数的图像,并从图像观察总结出正切函数的性质。
2. 教学用具:三角板、多媒体、实物投影仪.
3. 教学模式:启发、诱导发现教学、讲练结合
【授课类型】:新授课
【课时安排】:1课时
【教学思路】:
一、创设情景,揭示课题
1.回忆正、余弦函数的性质:定义域、值域、周期性、奇偶性、单调性。
2.求出下列函数的最小正周期,并说明下列函数是否有最大值、最小值,如果有,请写出取最大值、最小值时的自变量的集合. (1);(2).
3. 提问:如何比较与的大小?
4. 提问:能否类比研究正弦、余弦函数性质的方法来研究正切函数的图象和性质?
5.练习画下切线(分四个象限)
二、研探新知
1.正切函数的定义域是什么?
2.作的图象。原理:与正弦曲线一样通过正切线来作图
【说明】:(1)正切函数的最小正周期为;
(2)根据正切函数的周期性,我们可以把上述图象向左、右扩展,得到正切函数 ,的图象,并把它叫做正切曲线(如图1).
(3)由图象可以看出,正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的。
3.正切函数的性质
请同学们结合正切函数图象研究正切函数的性质:定义域、值域、周期性、奇偶性和单调性.
【学生活动】:观察函数的图象
【提问】:(1)的奇偶性怎样?为什么?除原点外,函数有无其它的对称中心?坐标怎样表示?
(2)函数的单调性怎样?能否认为函数在整个定义域上是增函数?函数会不会在某区间内是减函数?
引导学生观察,共同获得:
①定义域:正切函数的定义域是什么?
②值域:,没有最大值,也没有最小值;
观察:当从小于,时,
当从大于,时,。
③周期性:由诱导公式可知,正切函数是周期函数,最小正周期是.
④奇偶性:,∴正切函数是奇函数,正切曲线关于原点对称.
⑤单调性:由正切曲线图象可知:由正切线的变化规律可以看出,正切函数在内是增函数,又由正切函数的周期性可知,正切函数在开区间内都是增函数(在整个定义域内是增函数吗?)
⑥对称性:对称中心为(有对称轴吗 )
【强调】:a.不能说正切函数在整个定义域内是增函数
b.正切函数在每个单调区间内都是增函数
c.每个单调区间都包括两个象限:四、一或二、三
三、质疑答辩,排难解惑,发展思维
例1.(教材例4)求函数的定义域
例2.比较与的大小
例3.观察正切曲线写出满足下列条件的的值的范围:(1)(2)
例4.讨论函数的性质
四、巩固深化,反馈矫正
1.下列函数的单调增区间:(1)y=sin() (2) y=sin()
(3) (4) (5)
(6) (7) y=-cosx
【引申】:函数y=,在[ , ]是递 函数;
函数y=(cosx),在[ 0, ]是递 函数
2.(1)比较大小;
(2); (3)
3.判断下列函数的奇偶性
(1) y=sin(-2x) (2)f(x)=sin4x-cos4x+cos2x;
(3) (4)y=cosxlg(sinx+)
(5)f(x)=sin(2x+)
【引申】:已知(a、b为常数),且,求
4.(1)函数图象的对称轴是 ;对称中心是 .
(2)函数的对称轴是________;(3)的对称轴是________
(4)的对称中心为
(5)函数的图象的对称轴方程是_______
5. 求下列函数的最大值及取得最大值时自变量的集合:
(1);(2)
6. 求下列函数的最小正周期:(1) y=|sinx| (2)y=|sinx|+|cosx|
7. 根据正弦函数、余弦函数的图象,写出使下列不等式成立的x的集合
(1)sinx≥ (2)cosx≤- (3)2cosx-1>0
(1)sinx≥(x∈R) (2)+2cosx≥0 (x∈R)
五、归纳整理,整体认识
(1)这节课我们采用类比的思想方法来学习正切函数的图象和性质
(2)正切函数的作图是利用平移正切线得到的,当我们获得一个周期上图象后,再利用周期性把该段图象向左右延伸、平移。
因为正切函数的定义域是,所以它的图象被等相互平行的直线所隔开,而在相邻平行线间的图象是连续的。作出正切函数的图象,是先作出长度为一个周期(-π/2,π/2)的区间内的函数的图象,然后再将它沿轴向左或向右移动,每次移动的距离是π个单位,就可以得到整个正切函数的图象。
(3)正切函数的性质(周期的求法、奇偶性的判断、单调区间的求法)
讨论函数的单调性应借助图象或相关的函数的单调性;形如,≠ (k∈Z)的周期T=;注意正切函数的图象是由不连续的无数条曲线组成的
六、承上启下,留下悬念
预习函数y=Asin(ωx+φ)的图象
七、板书设计(略)
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
y
y
0
x
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
