2024年湖北省武汉市中考数学复习专题——常见相似模型课件(25张PPT)
文档属性
| 名称 | 2024年湖北省武汉市中考数学复习专题——常见相似模型课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 14:56:30 | ||
图片预览



文档简介
(共25张PPT)
常见相似模型
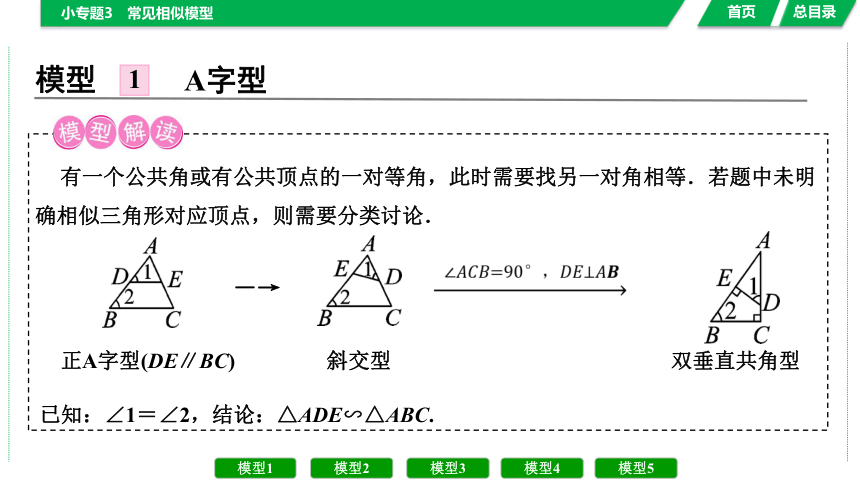
有一个公共角或有公共顶点的一对等角,此时需要找另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论.
A字型
模型
1
―→
正A字型(DE∥BC) 斜交型 双垂直共角型
已知:∠1=∠2,结论:△ADE∽△ABC.
1.(2023·杭州) 如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直
线DE对称.设=k,若AD=DF,则=_________(结果用含k的代数式表示).
线段等
直角三角形ABF , BCF
等腰三角形EFC
与
斜A型相似)
有一个公共角,又已知一对角相等,可以得到两个三角形相似.不仅要熟记模型,还要熟记模型的结论,当题目中给出三角形边的乘积或比例关系时,要能快速地判断题中的相似三角形,模型中由△ACD ∽△ABC可以得到AC2=AD·AB.
母子型
模型
2
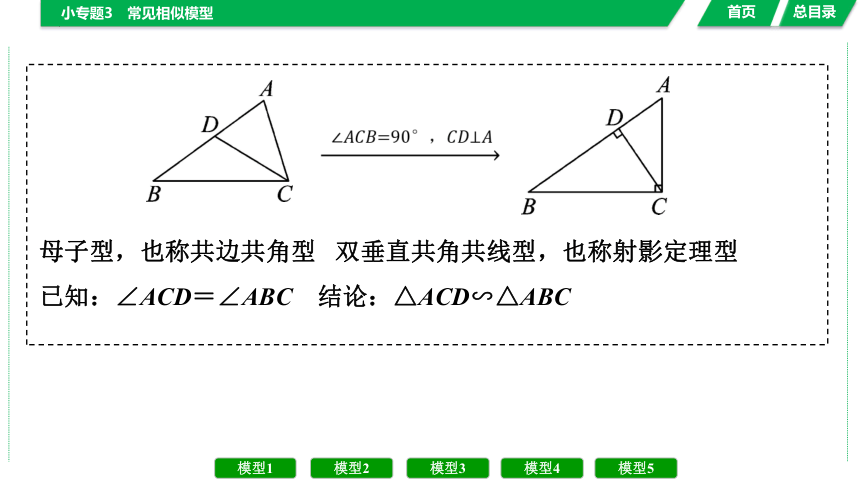
母子型,也称共边共角型 双垂直共角共线型,也称射影定理型
已知:∠ACD=∠ABC 结论:△ACD∽△ABC
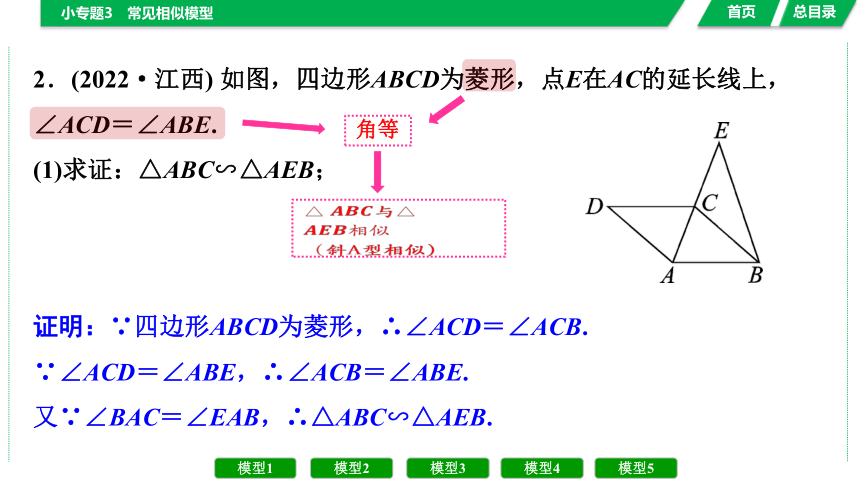
2.(2022·江西) 如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
证明:∵四边形ABCD为菱形,∴∠ACD=∠ACB.
∵∠ACD=∠ABE,∴∠ACB=∠ABE.
又∵∠BAC=∠EAB,∴△ABC∽△AEB.
角等
与
斜A型相似)
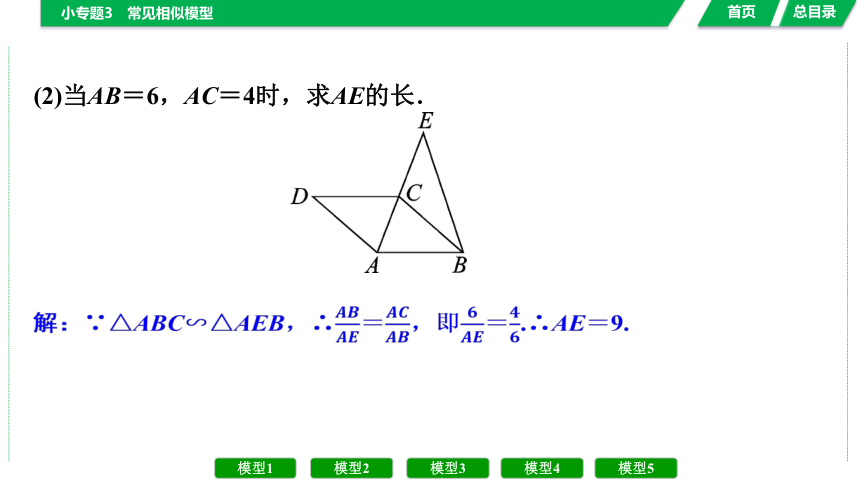
(2)当AB=6,AC=4时,求AE的长.
解:∵△ABC∽△AEB,∴=,即=.∴AE=9.
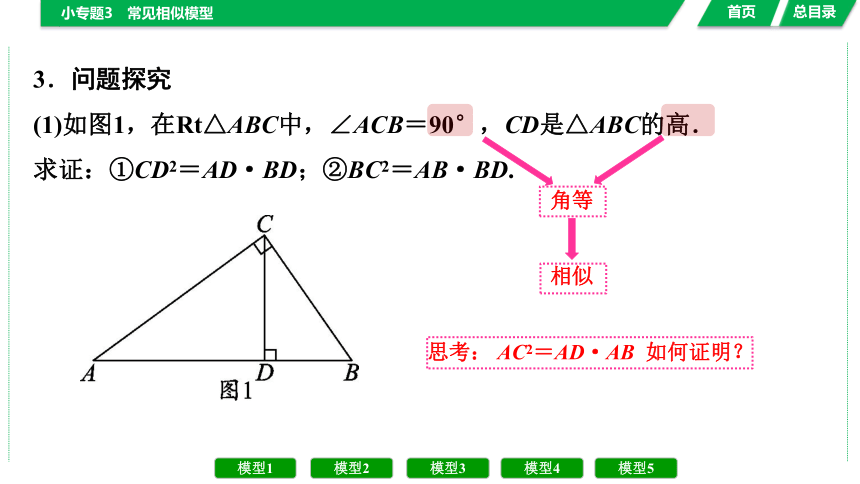
3.问题探究
(1)如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高.
求证:①CD2=AD·BD;②BC2=AB·BD.
角等
相似
思考: AC2=AD·AB 如何证明?
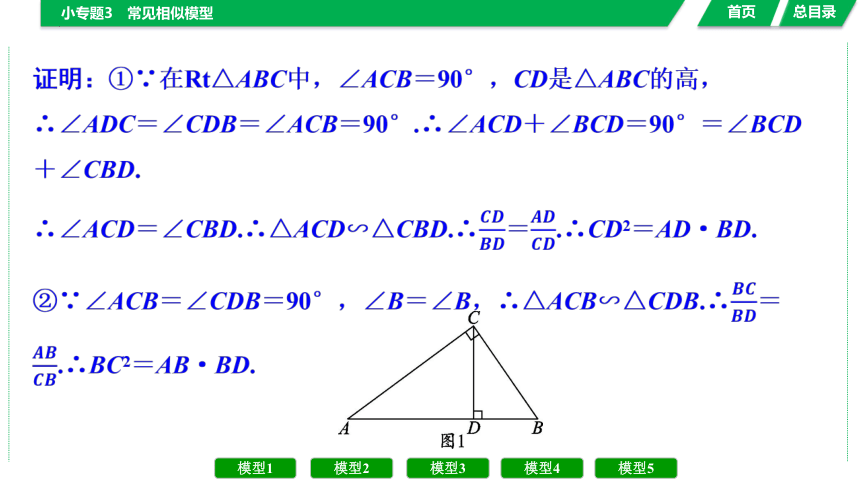
证明:①∵在Rt△ABC中,∠ACB=90°,CD是△ABC的高,
∴∠ADC=∠CDB=∠ACB=90°.∴∠ACD+∠BCD=90°=∠BCD+∠CBD.
∴∠ACD=∠CBD.∴△ACD∽△CBD.∴=.∴CD2=AD·BD.
②∵∠ACB=∠CDB=90°,∠B=∠B,∴△ACB∽△CDB.∴=.∴BC2=AB·BD.
迁移运用
(2)如图2,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,若BE=4,CD=6,求CE的长.
解:图2中,延长BO交AD于点G,连接OD.
∵OA=OD,AB=BD,∴直线BG是线段AD的垂
直平分线.∴∠AGO=90°,AG=DG.
∵BE⊥AC,∴∠AGO=∠BEO=90°.
又∵∠AOG=∠BOE,OA=OB,∴△AGO≌△BEO(AAS).
注意:证垂直的规范
充分运用题目中的相等线段(包括半径=半径)和相等角(尤其是直角)挖掘图中的全等三角形和相似三角形
∴AG=BE=4.∴DG=AG=4.∴AD=8.
∵AC是⊙O的直径,∴∠ABC=∠ADC=90°.
∵CD=6,∴AC==10.
∵∠ABC=∠AEB=∠BEC=90°,∴∠BAE+
∠ABE=90°,∠ABE+∠CBE=90°.
∴∠BAE=∠CBE.∴△ABE∽△BCE.∴=.∴=.∴CE=2或8(舍去).
∴CE的长为2.
射影型相似
有一组隐含的等角(对顶角),需要从已知条件、图中隐含条件或通过证明得到另一对角相等.若题中未明确指出相似三角形对应顶点,则需要分类讨论.
8字型
模型
3
AB∥CD正8字型
∠A=∠C或∠B=∠D斜8字型
AB∥CD∥EF三平行型
∠A=∠C或∠ABF=∠CDF共享型
4.(2023·乐山) 如图,在平行四边形ABCD中,E是线段AB上一点,连
接AC,DE交于点F.若=,则=______.
平行
线段相等
八字型相似
5.如图,已知在△ABC中,AB=AC,点D,E分别在边CB,AC的延长线上,且∠DAB=∠EBC,EB的延长线交AD于点F.
(1)求证:△DBF∽△EBC;
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠ABC,∠ACB分别是△ADB和△BCE的外角,
∴∠ABC=∠DAB+∠D,∠ACB=∠EBC+∠E.
∵∠DAB=∠EBC,∴∠D=∠E.
又∵∠DBF=∠EBC,∴△DBF∽△EBC.
角相等
相似(八字型)
相似(斜A型)
(2)如果AB=BC,求证:EC2=DF·DA.
证明:∵∠DBF=∠EBC,∠DAB=∠EBC,
∴∠DBF=∠DAB.
又∵∠D=∠D,∴△DBF∽△DAB.∴=,
即DB2=DF·DA.
在△ADB和△BEC中,∴△ADB≌△BEC(AAS).
∴DB=EC.∴EC2=DF·DA.
根据两组对应边之比始终相等,以及旋转角相等得到两个三角形相似,该模型的难度较大,常出现在压轴题中,以直角三角形为背景出题,对考生的综合能力要求较高,考查知识点有相似,旋转、勾股定理、锐角三角函数等.
“手拉手”旋转型
模型
4
6.(1)如图1,△ABC和△ADE都是等边三角形,连接BD,CE,求证:BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠BAE=∠DAE-∠BAE.∴∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).∴BD=CE.
共顶点的等边三角形
手拉手全等
(2)如图2,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,AB=BC,连接BD,CE,求的值.
解:∵AB=BC,设BC=4x,则AB=3x.
∵△ABC是直角三角形,∠ABC=90°,
∴AC==5x.
∵∠ABC=∠ADE=90°,∠ACB=∠AED,
∴△ABC∽△ADE.∴=,∠DAE=∠BAC.
∴=,∠DAE-∠BAE=∠BAC-∠BAE.
∴∠DAB=∠EAC.∴△DAB∽△EAC.∴===.即的值为.
共锐角顶点的直角三角形
手拉手相似
1.点P在线段AB上(同侧型)
一线三等角型(K型)
模型
5
已知:∠1=∠2=∠3,结论:△APC∽△BDP.
2.点P在线段AB的延长线上(异侧型)
已知:∠1=∠2=∠3,结论:△APC∽△BDP.
7.(2023·东营) 如图,△ABC为等边三角形,点D,E分别在边BC,
AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
C
A.1.8
B.2.4
C.3
D.3.2
60°
一线三等角相似
先证∠CAD=∠BDE,再根据∠B=∠C=60°,得出△ADC ∽
△DEB,根据相似三角形的性质即可求出AD的长.
本讲内容结束
常见相似模型
有一个公共角或有公共顶点的一对等角,此时需要找另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论.
A字型
模型
1
―→
正A字型(DE∥BC) 斜交型 双垂直共角型
已知:∠1=∠2,结论:△ADE∽△ABC.
1.(2023·杭州) 如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直
线DE对称.设=k,若AD=DF,则=_________(结果用含k的代数式表示).
线段等
直角三角形ABF , BCF
等腰三角形EFC
与
斜A型相似)
有一个公共角,又已知一对角相等,可以得到两个三角形相似.不仅要熟记模型,还要熟记模型的结论,当题目中给出三角形边的乘积或比例关系时,要能快速地判断题中的相似三角形,模型中由△ACD ∽△ABC可以得到AC2=AD·AB.
母子型
模型
2
母子型,也称共边共角型 双垂直共角共线型,也称射影定理型
已知:∠ACD=∠ABC 结论:△ACD∽△ABC
2.(2022·江西) 如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.
(1)求证:△ABC∽△AEB;
证明:∵四边形ABCD为菱形,∴∠ACD=∠ACB.
∵∠ACD=∠ABE,∴∠ACB=∠ABE.
又∵∠BAC=∠EAB,∴△ABC∽△AEB.
角等
与
斜A型相似)
(2)当AB=6,AC=4时,求AE的长.
解:∵△ABC∽△AEB,∴=,即=.∴AE=9.
3.问题探究
(1)如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高.
求证:①CD2=AD·BD;②BC2=AB·BD.
角等
相似
思考: AC2=AD·AB 如何证明?
证明:①∵在Rt△ABC中,∠ACB=90°,CD是△ABC的高,
∴∠ADC=∠CDB=∠ACB=90°.∴∠ACD+∠BCD=90°=∠BCD+∠CBD.
∴∠ACD=∠CBD.∴△ACD∽△CBD.∴=.∴CD2=AD·BD.
②∵∠ACB=∠CDB=90°,∠B=∠B,∴△ACB∽△CDB.∴=.∴BC2=AB·BD.
迁移运用
(2)如图2,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,若BE=4,CD=6,求CE的长.
解:图2中,延长BO交AD于点G,连接OD.
∵OA=OD,AB=BD,∴直线BG是线段AD的垂
直平分线.∴∠AGO=90°,AG=DG.
∵BE⊥AC,∴∠AGO=∠BEO=90°.
又∵∠AOG=∠BOE,OA=OB,∴△AGO≌△BEO(AAS).
注意:证垂直的规范
充分运用题目中的相等线段(包括半径=半径)和相等角(尤其是直角)挖掘图中的全等三角形和相似三角形
∴AG=BE=4.∴DG=AG=4.∴AD=8.
∵AC是⊙O的直径,∴∠ABC=∠ADC=90°.
∵CD=6,∴AC==10.
∵∠ABC=∠AEB=∠BEC=90°,∴∠BAE+
∠ABE=90°,∠ABE+∠CBE=90°.
∴∠BAE=∠CBE.∴△ABE∽△BCE.∴=.∴=.∴CE=2或8(舍去).
∴CE的长为2.
射影型相似
有一组隐含的等角(对顶角),需要从已知条件、图中隐含条件或通过证明得到另一对角相等.若题中未明确指出相似三角形对应顶点,则需要分类讨论.
8字型
模型
3
AB∥CD正8字型
∠A=∠C或∠B=∠D斜8字型
AB∥CD∥EF三平行型
∠A=∠C或∠ABF=∠CDF共享型
4.(2023·乐山) 如图,在平行四边形ABCD中,E是线段AB上一点,连
接AC,DE交于点F.若=,则=______.
平行
线段相等
八字型相似
5.如图,已知在△ABC中,AB=AC,点D,E分别在边CB,AC的延长线上,且∠DAB=∠EBC,EB的延长线交AD于点F.
(1)求证:△DBF∽△EBC;
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠ABC,∠ACB分别是△ADB和△BCE的外角,
∴∠ABC=∠DAB+∠D,∠ACB=∠EBC+∠E.
∵∠DAB=∠EBC,∴∠D=∠E.
又∵∠DBF=∠EBC,∴△DBF∽△EBC.
角相等
相似(八字型)
相似(斜A型)
(2)如果AB=BC,求证:EC2=DF·DA.
证明:∵∠DBF=∠EBC,∠DAB=∠EBC,
∴∠DBF=∠DAB.
又∵∠D=∠D,∴△DBF∽△DAB.∴=,
即DB2=DF·DA.
在△ADB和△BEC中,∴△ADB≌△BEC(AAS).
∴DB=EC.∴EC2=DF·DA.
根据两组对应边之比始终相等,以及旋转角相等得到两个三角形相似,该模型的难度较大,常出现在压轴题中,以直角三角形为背景出题,对考生的综合能力要求较高,考查知识点有相似,旋转、勾股定理、锐角三角函数等.
“手拉手”旋转型
模型
4
6.(1)如图1,△ABC和△ADE都是等边三角形,连接BD,CE,求证:BD=CE.
证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠BAE=∠DAE-∠BAE.∴∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).∴BD=CE.
共顶点的等边三角形
手拉手全等
(2)如图2,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,AB=BC,连接BD,CE,求的值.
解:∵AB=BC,设BC=4x,则AB=3x.
∵△ABC是直角三角形,∠ABC=90°,
∴AC==5x.
∵∠ABC=∠ADE=90°,∠ACB=∠AED,
∴△ABC∽△ADE.∴=,∠DAE=∠BAC.
∴=,∠DAE-∠BAE=∠BAC-∠BAE.
∴∠DAB=∠EAC.∴△DAB∽△EAC.∴===.即的值为.
共锐角顶点的直角三角形
手拉手相似
1.点P在线段AB上(同侧型)
一线三等角型(K型)
模型
5
已知:∠1=∠2=∠3,结论:△APC∽△BDP.
2.点P在线段AB的延长线上(异侧型)
已知:∠1=∠2=∠3,结论:△APC∽△BDP.
7.(2023·东营) 如图,△ABC为等边三角形,点D,E分别在边BC,
AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
C
A.1.8
B.2.4
C.3
D.3.2
60°
一线三等角相似
先证∠CAD=∠BDE,再根据∠B=∠C=60°,得出△ADC ∽
△DEB,根据相似三角形的性质即可求出AD的长.
本讲内容结束
同课章节目录
