2024年湖北省武汉市中考数学专题复习专题——几何综合与探究课件(42张PPT)
文档属性
| 名称 | 2024年湖北省武汉市中考数学专题复习专题——几何综合与探究课件(42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览






文档简介
(共42张PPT)
几何综合与探究
类比应用与拓展探究题是近几年的常考题,其特点是“图形变化,结构不变;方法类似,思路顺延;类比渗透,知识迁移”.先探究特殊图形情况下的相关结论,再推广到一般图形,利用图形之间相通或不变的性质,结合相同的思路去解决问题.解决关键是对题中的变量过程进行分析,把握原有图形的特点,探究变化量的特点.一般情况下,问题之间的方法的关联性很强,常常通过类比字母、类比辅助线、类比结构、类比思路来解决类比探究问题.这类题目往往是数形结合、转化、从特殊到一般、类比和方程等思想的运用,综合性很强.
类比应用与拓展探究
类型
1
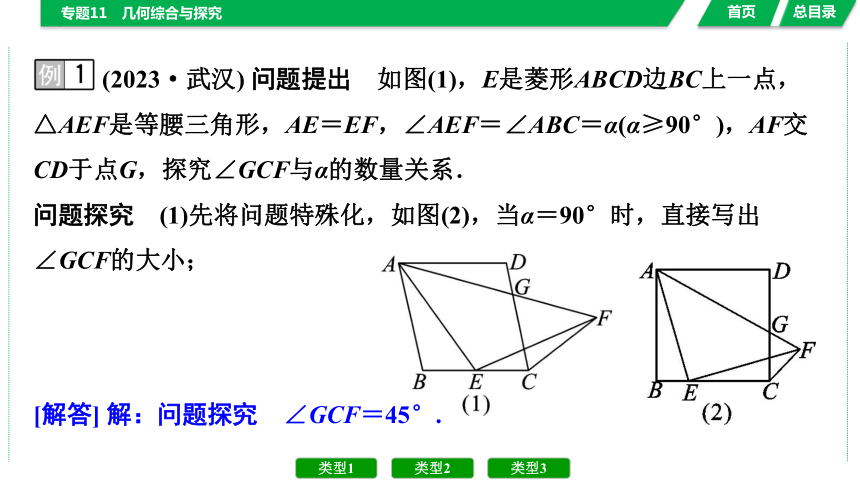
(2023·武汉) 问题提出 如图(1),E是菱形ABCD边BC上一点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°),AF交CD于点G,探究∠GCF与α的数量关系.
问题探究 (1)先将问题特殊化,如图(2),当α=90°时,直接写出∠GCF的大小;
[解答] 解:问题探究 ∠GCF=45°.
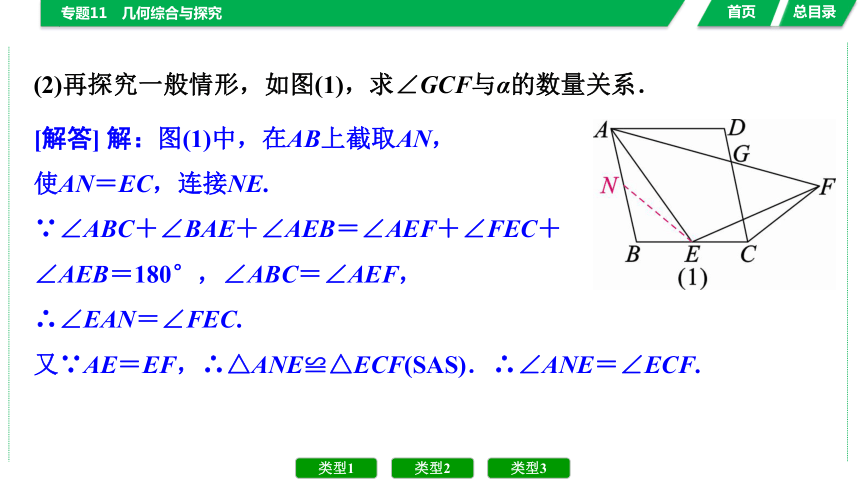
(2)再探究一般情形,如图(1),求∠GCF与α的数量关系.
[解答] 解:图(1)中,在AB上截取AN,
使AN=EC,连接NE.
∵∠ABC+∠BAE+∠AEB=∠AEF+∠FEC+
∠AEB=180°,∠ABC=∠AEF,
∴∠EAN=∠FEC.
又∵AE=EF,∴△ANE≌△ECF(SAS).∴∠ANE=∠ECF.
∵AB=BC,∴BN=BE.∵∠EBN=α,
∴∠BNE=90°-α.
∴∠GCF=∠ECF-∠BCD=∠ANE-∠BCD
=90°+α-(180°-α)=α-90°.
另解:连接AC,由△ABE∽△ACF,得∠ACF=∠ABC=α,则∠GCF=∠ACF-∠ACD=α-α-90°.
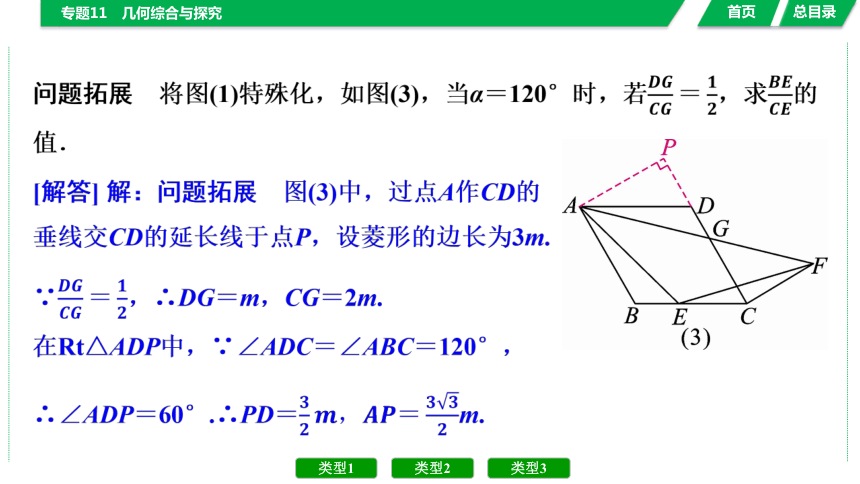
问题拓展 将图(1)特殊化,如图(3),当α=120°时,若,求的值.
[解答] 解:问题拓展 图(3)中,过点A作CD的
垂线交CD的延长线于点P,设菱形的边长为3m.
∵,∴DG=m,CG=2m.
在Rt△ADP中,∵∠ADC=∠ABC=120°,
∴∠ADP=60°.∴PD=m.
又α=120°,由(2)知,∠GCF=α-90°=90°.
∵∠AGP=∠FGC,∠P=∠GCF,∴△APG∽△FCG.
∴,即.∴FC=m.
由(2)知,BE=m,∴CE=m.∴.
另解:过点F作FM∥BC交CD于点M.
设菱形的边长为3m,BE=x,则CF=x,在Rt△CMF中,∠CMF=∠DCB=60°,CM=x,MF=2x.再根据建立方程,求出x即可.
变式1 (2023·武汉四调) 探索发现 如图(1),E,F,H分别是正方形ABCD边CD,DA,BC上三点,连接BE,CF交于点G,连接AG,GH,CE=DF.
(1)判定BE与CF的位置关系,并证明你的结论;
探索发现 解:BE与CF的位置关系是互相垂直.
证明:∵四边形ABCD是正方形,∴BC=CD,∠BCE=∠CDF=90°.
又∵CE=DF,∴△BCE≌△CDF(SAS).
∴∠CBE=∠DCF.∴∠CBE+∠CEG=∠DCF+∠CEG=90°.∴∠EGC=90°,即BE⊥CF.
(2)若CE=CH,求证:∠BAG=∠CHG.
证明:∵∠ECB=∠CGB=90°,∠CBE=∠GBC,∴△CEB∽△GCB.∴.
∵CE=CH,CB=AB,∴.∴.
∵∠GCB+∠GBC=∠GBA+∠GBC=90°,∴∠GCB=∠GBA.
∴△GCH∽△GBA.∴∠BAG=∠CHG.
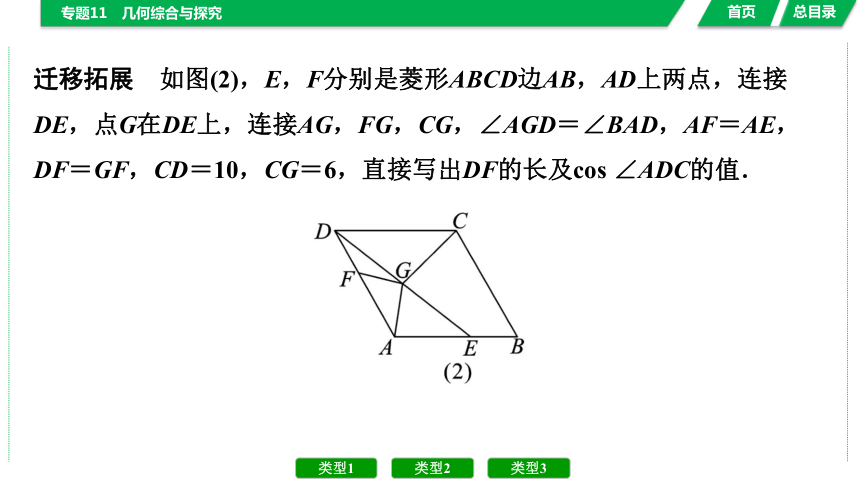
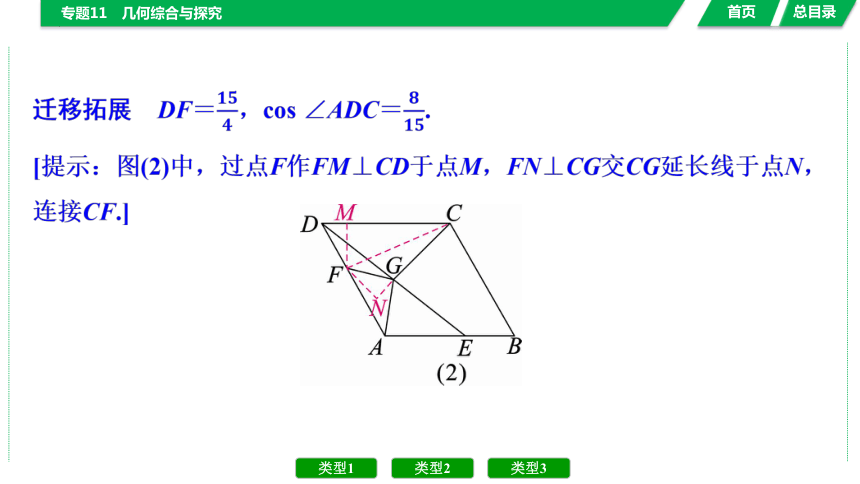
迁移拓展 如图(2),E,F分别是菱形ABCD边AB,AD上两点,连接DE,点G在DE上,连接AG,FG,CG,∠AGD=∠BAD,AF=AE,DF=GF,CD=10,CG=6,直接写出DF的长及cos ∠ADC的值.
迁移拓展 DF=,cos ∠ADC=.
[提示:图(2)中,过点F作FM⊥CD于点M,FN⊥CG交CG延长线于点N,连接CF.]
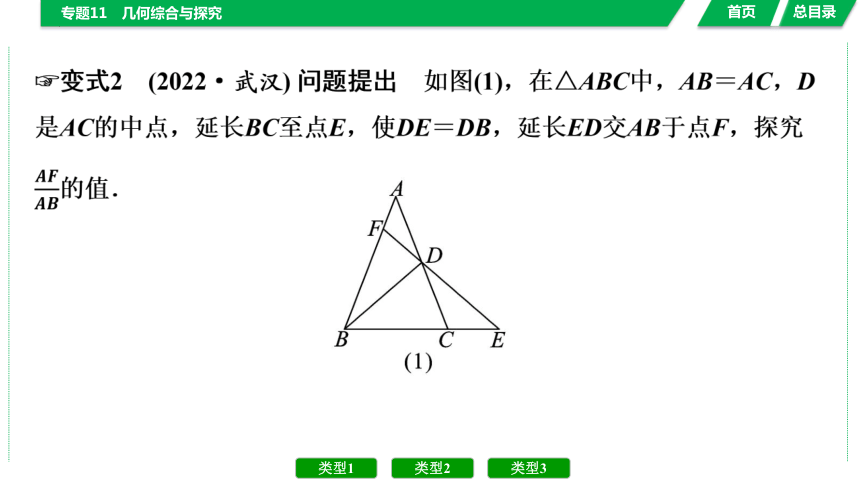
变式2 (2022·武汉) 问题提出 如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究 (1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
问题探究.
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
证明:图(1)中,取BC的中点H,连接DH.
∵D是AC的中点,∴DH∥AB,DH=AB.
∵AB=AC,∴DH=AC=DC.∴∠DHC=∠DCH.
∵BD=DE,∴∠DBH=∠DEC.
∴∠BDH=∠EDC.∴△DBH≌△DEC(ASA).
∴BH=EC=HC.∴.
∵DH∥AB,∴△EDH∽△EFB.∴.
∴.∴.
另解1:证明∠ADF=∠ABD,得△ADF∽△ABD也可求解.
另解2:取AB的中点M,证明△ECD≌△DMB也可求解.
问题拓展 如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
问题拓展 . [取BC的中点H,连接DH,由(2)同理可证明△DGH≌△DEC(ASA),∴GH=CE.∴HE=CG.∵.∴.∴.∴.∵DH∥BF,∴△EDH∽△EFB.∴.∵DH=AB,∴.∴.]
解决动点引起的类比探究题的一般思路通常需要先分析点在线段上运动的情况,运用相关知识,得到相关结论,再将问题进行升华,探究点在线段延长线上或反向延长线上的情况,抓住运动过程中不变的量和探究对象之间的关系,通过研究基本图形,分析运动过程,运用全等、相似、三角函数、勾股定理等知识,从特殊情况入手再到一般情形来解决问题.
动态问题探究
类型
2
(2023·青山区模拟) 在矩形ABCD中,E是对角线BD上一动点.点F在射线AB上运动,连接CE,EF,∠AFE=∠BCE.
(1)如图1,若AB=AD,F为线段AB上一点(不与端点A,B重合),求证:CE=EF且CE⊥EF;
[解答]证明:图1中,过点E作EH⊥BC于点H,EQ⊥AB于点Q.
∵AB=AD,∴矩形ABCD是正方形.∴∠ABE=∠CBE=45°.
∴EQ=EH.
在△FQE和△CHE中,
∴△FQE≌△CHE(AAS).∴CE=EF,∠QEF=∠CEH.
∴∠CEF=∠CEH+∠FEH=∠QEF+∠FEH=∠QEH=90°.∴CE⊥EF.
(2)如图2,点F在射线AB运动,①若BC=4,CD=3,探究线段CE与EF之间的关系,并说明理由;②在①的条件下,过点E作EH⊥BD交BC于点H,延长FE交AD边于点G,若△CDE是等腰三角形,直接写出的值.
解:①EF∶CE=4∶3且CE⊥EF,理由如下:
图2中,过点E作EH⊥BC于点H,EQ⊥AB于点Q.
∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°.
∴四边形BHEQ为矩形.∴∠QEH=90°,QE=BH.
∵∠FQE=∠CHE=90°,∠AFE=∠BCE,∴△QEF∽△HEC.
∴∠QEF=∠HEC,.∴∠CEF=∠CEH+
∠FEH=∠QEF+∠FEH=∠QEH=90°.
∴CE⊥EF.∵EH∥CD,∴△BEH∽△BDC.∴.
∵CD=3,BC=4,∴.∴.
②的值为或或. [若△CDE是等腰三角形,则分三种情况,利用
勾股定理、相似三角形等知识分别求出EH和CG的长度即可求出比值.]
变式 (2022·绍兴) 如图,在矩形ABCD中,AB=6,BC=8,动点E从点A出发,沿边AD,DC向点C运动,A,D关于直线BE的对称点分别为M,N,连接MN.
(1)如图,当点E在边AD上且DE=2时,求∠AEM的度数;
解:∵四边形ABCD是矩形,∴∠A=90°,AD=BC=8.
∵DE=2,∴AE=AB=6.∴∠AEB=∠ABE=45°.
如图1,由对称性知∠BEM=45°.∴∠AEM=90°.
(2)当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由;
解:如图2,∵AB=6,AD=8,∴BD=10.
∵当点N落在BC的延长线上时,BN=BD=10,∴CN=2.
由对称性,得∠ENC=∠BDC,DE=EN.
∴cos ∠ENC==cos ∠BDC=.∴.
∴EN=.∴DE=EN=.
MN∥BD.理由:∵BN=BD,MN=AD=BC,
∴Rt△BMN≌Rt△DCB(HL).∴∠DBC=∠BNM.∴MN∥BD.
(3)当直线MN恰好经过点C时,求DE的长.
解:如图3,当点E在边AD上时,BM=AB=6,∠BMC=∠A=90°=∠D.
∴MC=.
又∵BM=AB=CD,∠DEC=∠MCB,∴△BCM≌△CED(AAS).∴DE=MC=2;
如图4,当点E在边CD上时,连接AM,DN.
∵BM=AB=6,MN=AD=BC=8,
∴MC=2.
∵∠BMC=∠CNE=∠BCD=90°,
∴∠BCM+∠ECN=90°,∠BCM+∠CBM=90°.
∴∠CBM=∠ECN.∴△BMC∽△CNE.∴.
∴NE=.∴DE=NE=.
综上所述,DE的长为2或.
全等与相似的综合应用题是各地中考热点试题之一,这类题目考查的知识点多、条件隐晦,主要考查学生综合应用所学几何知识进行分析、推理、论证的能力.要求学生有较强的理解、分析、解决问题的能力,并有较强的创新意识与创新能力.
全等与相似的综合应用
类型
3
这类题常以全等形、相似形、勾股定理、三角函数等知识为考查重点,并贯穿其他几何、代数知识,以几何计算、证明、探究等题型出现.解决这类题目的关键是要对基本几何模型、常用辅助线、常用数学方法融会贯通;重视数形结合,多角度、全方位观察图形,挖掘隐含条件,寻找数量关系和相等关系;并要将几何图形的性质与代数知识以及计算与证明有机地融合起来.这类题目虽然难,但有梯度,一般题目中由浅入深有1~3个问题,解答这种题一般用综合法进行分析、推理,从而达到解决问题的目的.
(2023·宜昌) 如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点,
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
[解答]①证明:∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∵∠CEF=90°,∴∠AEF+∠CED=90°,
∠DCE+∠CED=90°.
∴∠AEF=∠DCE.∴△AEF∽△DCE.
②如图2,当tan ∠FCE=时,求AF的长.
解:图2中,延长DA交CF的延长线于点G,过点
G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED.∴.
∵CD=2,AE=ED=1,∴GH=2EH.设EH=m,GH=2m.
∵CE=,∴CH=m+.
∵tan ∠ECF=,∴.∴m=.
∴EH=.
∴EG=.
∴AG=EG-AE=.
∵AF∥CD,∴,即.∴AF=.
(2)如图3,延长CF,DA交于点G,当GE=DE,
sin ∠FCE=时,求证:AE=AF.
证明:图3中,过点G作GH⊥CE交CE的延长
线于点H.
设AD=CD=a,GE=DE=t,EH=x,
GH=y,CE=n.
∵∠H=∠D=90°,∠GEH=∠CED,∴△GEH∽△CED.
∴,即.∴x=.
在Rt△CGH中,sin ∠FCE=,
∴CG=3GH,CH=2GH.
∴x+n=2y,即.
∴t2+n2=2at.
在Rt△CDE中,n2=t2+a2,∴2at=2t2+a2.∴a=t.
∵AF∥CD,∴,即.∴AF==a-t.
∵AE=a-t,∴AE=AF.
变式 (2022·武汉四调) 如图,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别是边BC,AB上的点,∠ADC=∠EDB,过点E作EF⊥AD,垂足为F,交AC于点G.
(1)如图(1),求证:△AGE∽△BDE;
证明:∵EF⊥AD,∴∠AFG=90°.
又∵∠ACB=90°,∴∠AGF+∠GAF=
∠ADC+∠GAF=90°.∴∠AGF=∠ADC.
又∵∠ADC=∠EDB,∴∠AGF=∠EDB.
∵AC=BC,∴∠CAB=∠CBA.∴△AGE∽△BDE.
(2)如图(2),若点G恰好与顶点C重合,求证:BD=CD;
证明:图(2)中,过点B作BC的垂线交CE的延长线于点H.
∵∠ACF+∠DAC=∠ACF+∠HCB=90°,
∴∠DAC=∠HCB.
又∵∠ACD=∠CBH=90°,AC=CB,
∴△ACD≌△CBH(ASA).
∴CD=BH,∠ADC=∠CHB.∵∠ADC=∠BDE,
∴∠BDE=∠BHE.又∵∠DBE=∠HBE=45°,BE=BE,∴△BDE≌△BHE(AAS),∴BD=BH.∴BD=CD.
(3)如图(1),若,直接写出的值.
解:. [图(1)中,过点E作ET⊥BC于
点T.设CD=a.
∵,∴CB=CA=na.∴BD=BC-CD
=na-a=(n-1)a.
设DT=x,则BT=CB-CD-DT=na-a-x.
∵∠C=∠ETD=90°,∠ADC=∠EDT,
∴△ADC∽△EDT.∴,即.∴ET=nx.
∵∠B=45°,∴△ETB为等腰直角三角形.
∴ET=BT,BE=nx.
∴nx=na-a-x.∴x=.
∵AB=na,∴AE=AB-BE=
n(a-x).
∵△AGE∽△BDE,∴,即.
∴.∴AG=2a.∴.]
本讲内容结束
几何综合与探究
类比应用与拓展探究题是近几年的常考题,其特点是“图形变化,结构不变;方法类似,思路顺延;类比渗透,知识迁移”.先探究特殊图形情况下的相关结论,再推广到一般图形,利用图形之间相通或不变的性质,结合相同的思路去解决问题.解决关键是对题中的变量过程进行分析,把握原有图形的特点,探究变化量的特点.一般情况下,问题之间的方法的关联性很强,常常通过类比字母、类比辅助线、类比结构、类比思路来解决类比探究问题.这类题目往往是数形结合、转化、从特殊到一般、类比和方程等思想的运用,综合性很强.
类比应用与拓展探究
类型
1
(2023·武汉) 问题提出 如图(1),E是菱形ABCD边BC上一点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°),AF交CD于点G,探究∠GCF与α的数量关系.
问题探究 (1)先将问题特殊化,如图(2),当α=90°时,直接写出∠GCF的大小;
[解答] 解:问题探究 ∠GCF=45°.
(2)再探究一般情形,如图(1),求∠GCF与α的数量关系.
[解答] 解:图(1)中,在AB上截取AN,
使AN=EC,连接NE.
∵∠ABC+∠BAE+∠AEB=∠AEF+∠FEC+
∠AEB=180°,∠ABC=∠AEF,
∴∠EAN=∠FEC.
又∵AE=EF,∴△ANE≌△ECF(SAS).∴∠ANE=∠ECF.
∵AB=BC,∴BN=BE.∵∠EBN=α,
∴∠BNE=90°-α.
∴∠GCF=∠ECF-∠BCD=∠ANE-∠BCD
=90°+α-(180°-α)=α-90°.
另解:连接AC,由△ABE∽△ACF,得∠ACF=∠ABC=α,则∠GCF=∠ACF-∠ACD=α-α-90°.
问题拓展 将图(1)特殊化,如图(3),当α=120°时,若,求的值.
[解答] 解:问题拓展 图(3)中,过点A作CD的
垂线交CD的延长线于点P,设菱形的边长为3m.
∵,∴DG=m,CG=2m.
在Rt△ADP中,∵∠ADC=∠ABC=120°,
∴∠ADP=60°.∴PD=m.
又α=120°,由(2)知,∠GCF=α-90°=90°.
∵∠AGP=∠FGC,∠P=∠GCF,∴△APG∽△FCG.
∴,即.∴FC=m.
由(2)知,BE=m,∴CE=m.∴.
另解:过点F作FM∥BC交CD于点M.
设菱形的边长为3m,BE=x,则CF=x,在Rt△CMF中,∠CMF=∠DCB=60°,CM=x,MF=2x.再根据建立方程,求出x即可.
变式1 (2023·武汉四调) 探索发现 如图(1),E,F,H分别是正方形ABCD边CD,DA,BC上三点,连接BE,CF交于点G,连接AG,GH,CE=DF.
(1)判定BE与CF的位置关系,并证明你的结论;
探索发现 解:BE与CF的位置关系是互相垂直.
证明:∵四边形ABCD是正方形,∴BC=CD,∠BCE=∠CDF=90°.
又∵CE=DF,∴△BCE≌△CDF(SAS).
∴∠CBE=∠DCF.∴∠CBE+∠CEG=∠DCF+∠CEG=90°.∴∠EGC=90°,即BE⊥CF.
(2)若CE=CH,求证:∠BAG=∠CHG.
证明:∵∠ECB=∠CGB=90°,∠CBE=∠GBC,∴△CEB∽△GCB.∴.
∵CE=CH,CB=AB,∴.∴.
∵∠GCB+∠GBC=∠GBA+∠GBC=90°,∴∠GCB=∠GBA.
∴△GCH∽△GBA.∴∠BAG=∠CHG.
迁移拓展 如图(2),E,F分别是菱形ABCD边AB,AD上两点,连接DE,点G在DE上,连接AG,FG,CG,∠AGD=∠BAD,AF=AE,DF=GF,CD=10,CG=6,直接写出DF的长及cos ∠ADC的值.
迁移拓展 DF=,cos ∠ADC=.
[提示:图(2)中,过点F作FM⊥CD于点M,FN⊥CG交CG延长线于点N,连接CF.]
变式2 (2022·武汉) 问题提出 如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究 (1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
问题探究.
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
证明:图(1)中,取BC的中点H,连接DH.
∵D是AC的中点,∴DH∥AB,DH=AB.
∵AB=AC,∴DH=AC=DC.∴∠DHC=∠DCH.
∵BD=DE,∴∠DBH=∠DEC.
∴∠BDH=∠EDC.∴△DBH≌△DEC(ASA).
∴BH=EC=HC.∴.
∵DH∥AB,∴△EDH∽△EFB.∴.
∴.∴.
另解1:证明∠ADF=∠ABD,得△ADF∽△ABD也可求解.
另解2:取AB的中点M,证明△ECD≌△DMB也可求解.
问题拓展 如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
问题拓展 . [取BC的中点H,连接DH,由(2)同理可证明△DGH≌△DEC(ASA),∴GH=CE.∴HE=CG.∵.∴.∴.∴.∵DH∥BF,∴△EDH∽△EFB.∴.∵DH=AB,∴.∴.]
解决动点引起的类比探究题的一般思路通常需要先分析点在线段上运动的情况,运用相关知识,得到相关结论,再将问题进行升华,探究点在线段延长线上或反向延长线上的情况,抓住运动过程中不变的量和探究对象之间的关系,通过研究基本图形,分析运动过程,运用全等、相似、三角函数、勾股定理等知识,从特殊情况入手再到一般情形来解决问题.
动态问题探究
类型
2
(2023·青山区模拟) 在矩形ABCD中,E是对角线BD上一动点.点F在射线AB上运动,连接CE,EF,∠AFE=∠BCE.
(1)如图1,若AB=AD,F为线段AB上一点(不与端点A,B重合),求证:CE=EF且CE⊥EF;
[解答]证明:图1中,过点E作EH⊥BC于点H,EQ⊥AB于点Q.
∵AB=AD,∴矩形ABCD是正方形.∴∠ABE=∠CBE=45°.
∴EQ=EH.
在△FQE和△CHE中,
∴△FQE≌△CHE(AAS).∴CE=EF,∠QEF=∠CEH.
∴∠CEF=∠CEH+∠FEH=∠QEF+∠FEH=∠QEH=90°.∴CE⊥EF.
(2)如图2,点F在射线AB运动,①若BC=4,CD=3,探究线段CE与EF之间的关系,并说明理由;②在①的条件下,过点E作EH⊥BD交BC于点H,延长FE交AD边于点G,若△CDE是等腰三角形,直接写出的值.
解:①EF∶CE=4∶3且CE⊥EF,理由如下:
图2中,过点E作EH⊥BC于点H,EQ⊥AB于点Q.
∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°.
∴四边形BHEQ为矩形.∴∠QEH=90°,QE=BH.
∵∠FQE=∠CHE=90°,∠AFE=∠BCE,∴△QEF∽△HEC.
∴∠QEF=∠HEC,.∴∠CEF=∠CEH+
∠FEH=∠QEF+∠FEH=∠QEH=90°.
∴CE⊥EF.∵EH∥CD,∴△BEH∽△BDC.∴.
∵CD=3,BC=4,∴.∴.
②的值为或或. [若△CDE是等腰三角形,则分三种情况,利用
勾股定理、相似三角形等知识分别求出EH和CG的长度即可求出比值.]
变式 (2022·绍兴) 如图,在矩形ABCD中,AB=6,BC=8,动点E从点A出发,沿边AD,DC向点C运动,A,D关于直线BE的对称点分别为M,N,连接MN.
(1)如图,当点E在边AD上且DE=2时,求∠AEM的度数;
解:∵四边形ABCD是矩形,∴∠A=90°,AD=BC=8.
∵DE=2,∴AE=AB=6.∴∠AEB=∠ABE=45°.
如图1,由对称性知∠BEM=45°.∴∠AEM=90°.
(2)当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由;
解:如图2,∵AB=6,AD=8,∴BD=10.
∵当点N落在BC的延长线上时,BN=BD=10,∴CN=2.
由对称性,得∠ENC=∠BDC,DE=EN.
∴cos ∠ENC==cos ∠BDC=.∴.
∴EN=.∴DE=EN=.
MN∥BD.理由:∵BN=BD,MN=AD=BC,
∴Rt△BMN≌Rt△DCB(HL).∴∠DBC=∠BNM.∴MN∥BD.
(3)当直线MN恰好经过点C时,求DE的长.
解:如图3,当点E在边AD上时,BM=AB=6,∠BMC=∠A=90°=∠D.
∴MC=.
又∵BM=AB=CD,∠DEC=∠MCB,∴△BCM≌△CED(AAS).∴DE=MC=2;
如图4,当点E在边CD上时,连接AM,DN.
∵BM=AB=6,MN=AD=BC=8,
∴MC=2.
∵∠BMC=∠CNE=∠BCD=90°,
∴∠BCM+∠ECN=90°,∠BCM+∠CBM=90°.
∴∠CBM=∠ECN.∴△BMC∽△CNE.∴.
∴NE=.∴DE=NE=.
综上所述,DE的长为2或.
全等与相似的综合应用题是各地中考热点试题之一,这类题目考查的知识点多、条件隐晦,主要考查学生综合应用所学几何知识进行分析、推理、论证的能力.要求学生有较强的理解、分析、解决问题的能力,并有较强的创新意识与创新能力.
全等与相似的综合应用
类型
3
这类题常以全等形、相似形、勾股定理、三角函数等知识为考查重点,并贯穿其他几何、代数知识,以几何计算、证明、探究等题型出现.解决这类题目的关键是要对基本几何模型、常用辅助线、常用数学方法融会贯通;重视数形结合,多角度、全方位观察图形,挖掘隐含条件,寻找数量关系和相等关系;并要将几何图形的性质与代数知识以及计算与证明有机地融合起来.这类题目虽然难,但有梯度,一般题目中由浅入深有1~3个问题,解答这种题一般用综合法进行分析、推理,从而达到解决问题的目的.
(2023·宜昌) 如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点,
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
[解答]①证明:∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∵∠CEF=90°,∴∠AEF+∠CED=90°,
∠DCE+∠CED=90°.
∴∠AEF=∠DCE.∴△AEF∽△DCE.
②如图2,当tan ∠FCE=时,求AF的长.
解:图2中,延长DA交CF的延长线于点G,过点
G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED.∴.
∵CD=2,AE=ED=1,∴GH=2EH.设EH=m,GH=2m.
∵CE=,∴CH=m+.
∵tan ∠ECF=,∴.∴m=.
∴EH=.
∴EG=.
∴AG=EG-AE=.
∵AF∥CD,∴,即.∴AF=.
(2)如图3,延长CF,DA交于点G,当GE=DE,
sin ∠FCE=时,求证:AE=AF.
证明:图3中,过点G作GH⊥CE交CE的延长
线于点H.
设AD=CD=a,GE=DE=t,EH=x,
GH=y,CE=n.
∵∠H=∠D=90°,∠GEH=∠CED,∴△GEH∽△CED.
∴,即.∴x=.
在Rt△CGH中,sin ∠FCE=,
∴CG=3GH,CH=2GH.
∴x+n=2y,即.
∴t2+n2=2at.
在Rt△CDE中,n2=t2+a2,∴2at=2t2+a2.∴a=t.
∵AF∥CD,∴,即.∴AF==a-t.
∵AE=a-t,∴AE=AF.
变式 (2022·武汉四调) 如图,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别是边BC,AB上的点,∠ADC=∠EDB,过点E作EF⊥AD,垂足为F,交AC于点G.
(1)如图(1),求证:△AGE∽△BDE;
证明:∵EF⊥AD,∴∠AFG=90°.
又∵∠ACB=90°,∴∠AGF+∠GAF=
∠ADC+∠GAF=90°.∴∠AGF=∠ADC.
又∵∠ADC=∠EDB,∴∠AGF=∠EDB.
∵AC=BC,∴∠CAB=∠CBA.∴△AGE∽△BDE.
(2)如图(2),若点G恰好与顶点C重合,求证:BD=CD;
证明:图(2)中,过点B作BC的垂线交CE的延长线于点H.
∵∠ACF+∠DAC=∠ACF+∠HCB=90°,
∴∠DAC=∠HCB.
又∵∠ACD=∠CBH=90°,AC=CB,
∴△ACD≌△CBH(ASA).
∴CD=BH,∠ADC=∠CHB.∵∠ADC=∠BDE,
∴∠BDE=∠BHE.又∵∠DBE=∠HBE=45°,BE=BE,∴△BDE≌△BHE(AAS),∴BD=BH.∴BD=CD.
(3)如图(1),若,直接写出的值.
解:. [图(1)中,过点E作ET⊥BC于
点T.设CD=a.
∵,∴CB=CA=na.∴BD=BC-CD
=na-a=(n-1)a.
设DT=x,则BT=CB-CD-DT=na-a-x.
∵∠C=∠ETD=90°,∠ADC=∠EDT,
∴△ADC∽△EDT.∴,即.∴ET=nx.
∵∠B=45°,∴△ETB为等腰直角三角形.
∴ET=BT,BE=nx.
∴nx=na-a-x.∴x=.
∵AB=na,∴AE=AB-BE=
n(a-x).
∵△AGE∽△BDE,∴,即.
∴.∴AG=2a.∴.]
本讲内容结束
同课章节目录
