数学:1.3.4《三角函数的应用(二)》教案(苏教版必修4)
文档属性
| 名称 | 数学:1.3.4《三角函数的应用(二)》教案(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 80.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-19 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第 15 课时:§1.3.4 三角函数的应用(二)
【三维目标】:
一、知识与技能
1. 会用三角函数的图象和性质解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型.
2.掌握三角函数模型应用基本步骤:(1)根据图象建立解析式;(2)根据解析式作出图象; (3)将实际问题抽象为与三角函数有关的简单函数模型.
3.能正确分析收集到的数据,选择恰当的函数模型刻画数据所蕴含的规律,能根据问题的实际意义,利用模型解释有关实际问题,为决策提供依据。
4.让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的建模、分析问题、数形结合、抽象概括等能力.培养学生用已有的知识解决实际问题的能力. 培养学生数学应用意识;提高学生利用信息技术处理一些实际计算的能力。
二、过程与方法
1.从实际的应用中体会数学与生活是相关的,不是完全脱离现实的,同时理解三角函数在描述周期性现象时的重要作用。
2.讲解例题,总结方法,巩固练习。
三、情感、态度与价值观
1.培养学生应用数学的能力,让学生体会到数学在实际生活中的应用,意识到只要认真观察思考,会发现数学来源于生活。
2.让学生切身感受数学建模的过程,体验数学在解决实际问题中的价值和作用,从而激发学生的学习兴趣,培养锲而不舍的钻研精神;
3.培养学生勇于探索、勤于思考的精神。
【教学重点与难点】:
重点:用三角函数模型刻画潮汐等现象的变化规律,用函数思想解决具有周期变化的实际问题;对问题实际意义的数学解释,从实际问题中抽象出三角函数模型。
难点:(1)分析、整理、利用信息,
从实际问题中抽取基本的数学关系来建立数学模型,
并调动相关学科的知识来解决问题.(2)由图象求解析式时的确定。
【学法与教学用具】:
1.学法:
2.教学用具:多媒体、实物投影仪.
【授课类型】:新授课
【课时安排】:1课时
【教学流程】:
实例背景,资料数据,提出问题
根据散点图形特征,选择适当的函数拟合
求解函数模型
利用函数模型解决实际问题
反思解题过程,总结解题方法,提炼数学思想
【教学思路】:
一、创设情景,揭示课题
【复习提问】:1.回顾教材“三角函数的周期性”;
2.求函数的解析式。(1) 函数f (x)的横坐标伸长为原来的2倍,再向左平移个单位所得的曲线是的图像,试求的解析式.(2) 函数的最小值是2,其图象最高点与最低点横坐标差是3,且图象过点(0,1),求函数解析式.
3.讨论:(1)如何由图观察得到三角函数的各系数? 如何确定初相?(特殊点法)
(2)在现实生活中,哪些现象具有周期性?(温度、白昼、振动、情绪、智力、体力等)函数y=Asin(ωx+φ)的性质问题,是三角函数中的重要问题,是高中数学的重点内容,也是高考的热点.三角函数能够模拟许多周期现象,因此在解决实际问题中有着广泛的应用.
二、研探新知
例1 (学生自学完成教材例1)
点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3cm,周期为3s,且物体向右运动到距平衡位置最远处时开始计时.
(1)求物体对平衡位置的位移(cm)和时间t(s)之间的函数关系;
(2)求该物体在t=5s时的位置.
(教师进行适当的评析.并回答下列问题:根据物理常识,应选择怎样的函数式模拟物体的运动;怎样求和初相位θ;第二问中的“t=5s时的位置”与函数式有何关系?)
例2(学生自学完成教材例2)一半径为的水轮如图1-3-22所示,水轮圆心距离水面,已知水轮每分钟转动4圈,如果当水轮上点从水中浮现时(图中点)开始计算时间。
(1)将点距离水面的高度表示为时间的函数;
(2)点第一次到达最高点大约要多长时间?
例3 (教材探究案例)海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般的早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮是返回海洋.下面给出了某港口在某季节每天几个时刻的水深.
时间 0.00 3.00 6.00 9.00 12.00 15.00 18.00 21.00 24.00
水深 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系,并给出在整点时的近似数值.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
【问题】:
(1)选择怎样的数学模型反映该实际问题?
(2)图表中的最大值与三角函数的哪个量有关?
(3)函数的周期为多少?
(4)“吃水深度”对应函数中的哪个字母?
请同学们看下面这个问题:
【问题探究1】:请同学们仔细观察表格中的数据,你能够从中得到一些什么信息?
小组合作发现,代表发言。可能结果:
1)水深的最大值是7.5米,最小值是2.5米。
2)水的深度开始由5.0米增加到7.5米,后逐渐减少一直减少到2.5,又开始逐渐变深,增加到7.5米后,又开始减少。
3)水深变化并不是杂乱无章,而是呈现一种周期性变化规律。
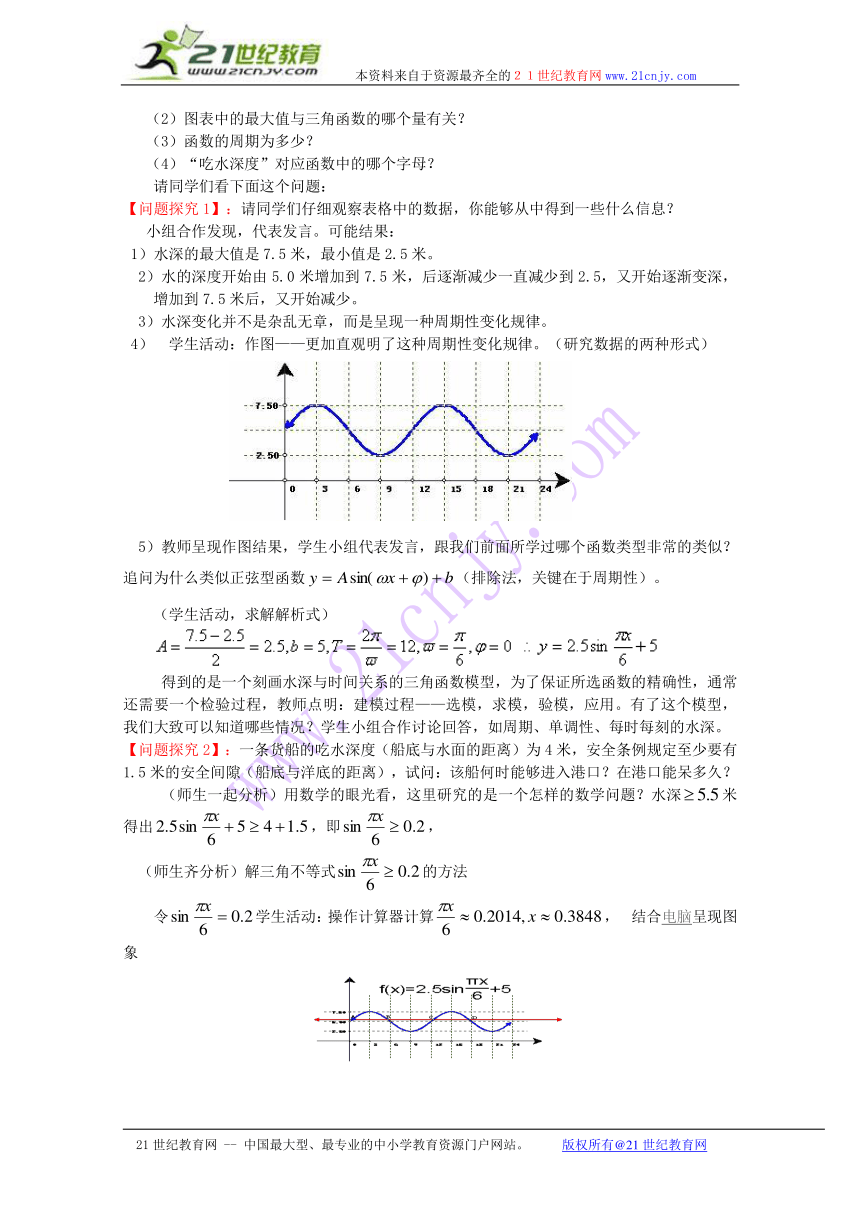
4) 学生活动:作图——更加直观明了这种周期性变化规律。(研究数据的两种形式)
5)教师呈现作图结果,学生小组代表发言,跟我们前面所学过哪个函数类型非常的类似?追问为什么类似正弦型函数(排除法,关键在于周期性)。
(学生活动,求解解析式)
得到的是一个刻画水深与时间关系的三角函数模型,为了保证所选函数的精确性,通常还需要一个检验过程,教师点明:建模过程——选模,求模,验模,应用。有了这个模型,我们大致可以知道哪些情况?学生小组合作讨论回答,如周期、单调性、每时每刻的水深。
【问题探究2】:一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
(师生一起分析)用数学的眼光看,这里研究的是一个怎样的数学问题?水深米得出,即,
(师生齐分析)解三角不等式的方法
令学生活动:操作计算器计算, 结合电脑 ( http: / / www. / " \t "_blank )呈现图象
发现:在[0,24]范围内,方程的解一共有4个,从小到大依次记为:
那么其他三个值如何求得呢?(学生思考)
得到了4个交点的横坐标值后,结合图象说说货船应该选择什么时间进港?什么时间出港呢?
(学生讨论,交流)
可能结果:【生1】货船可以在0时30分钟左右进港,早晨5时30分钟左右出港;或者是中午12时30分钟左右进港,在傍晚17时30分钟左右出港。
【生2】货船可以在0时30分钟左右进港,可以选择早晨5时30分,中午12时30分,或者傍晚17时30分左右出港。
……
(学生讨论,最后确定方案1为安全方案,因为当实际水深小于安全深度时,货船尽管没有行驶,但是搁浅后船身完全可以馅入淤泥,即使后来水位上涨,也很可能船身不再上浮)
刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随着船身自身重量的减小,船身会上浮,这样一来当两者都在改变的时候,我们又该如何选择进出港时间呢?请看下面问题:
【问题探究3】:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
(学生讨论)安全即需要:实际水深安全水深,即:
,
讨论求解方法:用代数的方法?几何的角度?(电脑 ( http: / / www. / " \t "_blank )作图并呈现)
通过图象可以看出,当快要到P时刻的时候,货船就要停止卸货,驶向深水区。那么P点的坐标如何求得呢?(学生思考,讨论,交流)求 P点横坐标即解方程
数形结合,二分法求近似解:
由图得点P点横坐标在[6,7],故我们只需要算出6,6.5,7三个时刻的安全水深与实际水深的数值表就可以回答上面的问题。
时间 实际水深 安全水深 是否安全
6.0 5米 4.3米 安全
6.5 4.2米 4.1米 较安全
7.0 3.8米 4.0米 危险
货船应该在6时30分左右驶离港口。(可能有的同学有些异议,可以讨论)
从这这个问题可以看出,如果有时候时间控制不当,货船在卸货的过程中,就会出现货还没有卸完,不得已要暂时驶离港口,进入深水区,等水位上涨后在驶回来。这样对公司来说就会造成才力、物力上的巨大浪费?那该怎么来做呢? (学生讨论)
可以加快卸货速度,也就是加快安全深度下降速度。
【问题探究4】:若船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,货物卸空后吃水深度为2米,为了保证进入码头后一次性卸空货物,又能安全驶离码头,那么每小时吃水深度至少要以多少速度减少?---探究3的变式(学生课后探究)
三、质疑答辩,排难解惑,发展思维
1.如图,单摆从某点给一个作用力后开始来回摆动,离开平衡位置O的距离s厘米和时间t秒的函数关系为.
(1)单摆摆动5秒时,离开平衡位置多少厘米?
(2)单摆摆动时,从最右边到最左边的距离为多少厘米?
(3)单摆来回摆动10次所需的时间为多少秒?
2.如图,某地一天从6~14时的温度变化曲线近似满足函数.
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
【问题的反思】:
①一般地,所求出的函数模型只能近似刻画这天某个时段的温度变化情况,因此应当特别注意自变量的变化范围;
②与学生一起探索的各种求法;(这是本题的关键!也是难点!)(用最大小值点代入不容易出现错误)
③如何根据图像求解析式中的待定参数
④探究其他解法:或 等
⑤借助三角函数模型研究的思想方法研究一些较复杂的三角函数。
四、巩固深化,反馈矫正
1.某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:小时)的函数,经过长期观察,该函数的图象可以近似地看成. 下表是测得的某日各时的浪高数据:
t(时) 0 3 6 9 12 15 18 21 24
y(米) 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
依规定,当浪高不低于1米时浴场才开放,试安排白天内开放浴场的具体时间段.
2.某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记为y=,下面是某日水深数据:
t(时) 0 3 6 9 12 15 18 21 24
y(米) 10.0 13.0 9.9 7.0 10.0 13.0 10.1 7.0 10.0
经过长期观察,y=的曲线可以近似看成y=Asint+b的图象.
(i)根据以上数据求出y=的近似表达式;
(ii)船底离海底5米或者5米以上是安全的,某船的吃水深度为6.5米(船底离水面距离),如果此船在凌晨4点进港,希望在同一天安全出港,那么此船最多在港口停留多少时间?
教法:从表中读到一些什么数据? → 依次求各系数 → 应用模型解决问题
答案:(0≤t≤24); 13(小时).
小结:读取与分析表中的数据,是一种数学思维能力的训练. 求得模型后,把第(2)问的情景转化为一个简单的三角不等式,再运用整体思想,借助函数的图象或者单位圆可以求解.
3.某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试建立出厂价格、销售价格的模型,并求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数.
五、归纳整理,整体认识
从以上问题可以发现三角函数知识在解决实际问题中有着十分广泛的应用,而待定系数法是三角函数中确定函数解析式最重要的方法.三角函数知识作为数学工具之一,在以后的学习中将经常有所涉及.学数学是为了用数学,通过学习我们逐步提高自己分析问题解决问题的能力.
三角函数应用模型的三种模式:一是给定呈周期变化规律的三角函数模型,根据所给模型,结合三角函数的性质,解决一些实际问题;而是给定呈周期变化的图象,利用待定系数法求出函数模型,再解决其他问题;三是搜集一个实际问题的调查数据,根据数据作出散点图,通过拟合函数图象,求出可以近似表示变化规律的函数模型,进一步用函数模型来解决问题.
回顾整个探究过程,经历了第一阶段:收集数据-----画散点图
第二阶段:根据图象特征---选模、求模、验模
第三阶段:函数模型应用
在整个探究过程,我们用到数学常见的一些思想方法:
(1)对实际问题处理过程是,首先是挖掘其中的数学本质,将实际问题转化为数学问题;体现了数学中的转化思想;
(2)在对一些数据处理的过程用到了估算的思想;
(3)在用代数方法处理困难的一些题目的解决中,用到了数形结合的思想;
(4)在方程的求解过程中,用到了算法中“二分法”思想。
六、承上启下,留下悬念
七、板书设计
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第 15 课时:§1.3.4 三角函数的应用(二)
【三维目标】:
一、知识与技能
1. 会用三角函数的图象和性质解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型.
2.掌握三角函数模型应用基本步骤:(1)根据图象建立解析式;(2)根据解析式作出图象; (3)将实际问题抽象为与三角函数有关的简单函数模型.
3.能正确分析收集到的数据,选择恰当的函数模型刻画数据所蕴含的规律,能根据问题的实际意义,利用模型解释有关实际问题,为决策提供依据。
4.让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的建模、分析问题、数形结合、抽象概括等能力.培养学生用已有的知识解决实际问题的能力. 培养学生数学应用意识;提高学生利用信息技术处理一些实际计算的能力。
二、过程与方法
1.从实际的应用中体会数学与生活是相关的,不是完全脱离现实的,同时理解三角函数在描述周期性现象时的重要作用。
2.讲解例题,总结方法,巩固练习。
三、情感、态度与价值观
1.培养学生应用数学的能力,让学生体会到数学在实际生活中的应用,意识到只要认真观察思考,会发现数学来源于生活。
2.让学生切身感受数学建模的过程,体验数学在解决实际问题中的价值和作用,从而激发学生的学习兴趣,培养锲而不舍的钻研精神;
3.培养学生勇于探索、勤于思考的精神。
【教学重点与难点】:
重点:用三角函数模型刻画潮汐等现象的变化规律,用函数思想解决具有周期变化的实际问题;对问题实际意义的数学解释,从实际问题中抽象出三角函数模型。
难点:(1)分析、整理、利用信息,
从实际问题中抽取基本的数学关系来建立数学模型,
并调动相关学科的知识来解决问题.(2)由图象求解析式时的确定。
【学法与教学用具】:
1.学法:
2.教学用具:多媒体、实物投影仪.
【授课类型】:新授课
【课时安排】:1课时
【教学流程】:
实例背景,资料数据,提出问题
根据散点图形特征,选择适当的函数拟合
求解函数模型
利用函数模型解决实际问题
反思解题过程,总结解题方法,提炼数学思想
【教学思路】:
一、创设情景,揭示课题
【复习提问】:1.回顾教材“三角函数的周期性”;
2.求函数的解析式。(1) 函数f (x)的横坐标伸长为原来的2倍,再向左平移个单位所得的曲线是的图像,试求的解析式.(2) 函数的最小值是2,其图象最高点与最低点横坐标差是3,且图象过点(0,1),求函数解析式.
3.讨论:(1)如何由图观察得到三角函数的各系数? 如何确定初相?(特殊点法)
(2)在现实生活中,哪些现象具有周期性?(温度、白昼、振动、情绪、智力、体力等)函数y=Asin(ωx+φ)的性质问题,是三角函数中的重要问题,是高中数学的重点内容,也是高考的热点.三角函数能够模拟许多周期现象,因此在解决实际问题中有着广泛的应用.
二、研探新知
例1 (学生自学完成教材例1)
点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3cm,周期为3s,且物体向右运动到距平衡位置最远处时开始计时.
(1)求物体对平衡位置的位移(cm)和时间t(s)之间的函数关系;
(2)求该物体在t=5s时的位置.
(教师进行适当的评析.并回答下列问题:根据物理常识,应选择怎样的函数式模拟物体的运动;怎样求和初相位θ;第二问中的“t=5s时的位置”与函数式有何关系?)
例2(学生自学完成教材例2)一半径为的水轮如图1-3-22所示,水轮圆心距离水面,已知水轮每分钟转动4圈,如果当水轮上点从水中浮现时(图中点)开始计算时间。
(1)将点距离水面的高度表示为时间的函数;
(2)点第一次到达最高点大约要多长时间?
例3 (教材探究案例)海水受日月的引力,在一定的时候发生涨落的现象叫潮汐,一般的早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮是返回海洋.下面给出了某港口在某季节每天几个时刻的水深.
时间 0.00 3.00 6.00 9.00 12.00 15.00 18.00 21.00 24.00
水深 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系,并给出在整点时的近似数值.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
【问题】:
(1)选择怎样的数学模型反映该实际问题?
(2)图表中的最大值与三角函数的哪个量有关?
(3)函数的周期为多少?
(4)“吃水深度”对应函数中的哪个字母?
请同学们看下面这个问题:
【问题探究1】:请同学们仔细观察表格中的数据,你能够从中得到一些什么信息?
小组合作发现,代表发言。可能结果:
1)水深的最大值是7.5米,最小值是2.5米。
2)水的深度开始由5.0米增加到7.5米,后逐渐减少一直减少到2.5,又开始逐渐变深,增加到7.5米后,又开始减少。
3)水深变化并不是杂乱无章,而是呈现一种周期性变化规律。
4) 学生活动:作图——更加直观明了这种周期性变化规律。(研究数据的两种形式)
5)教师呈现作图结果,学生小组代表发言,跟我们前面所学过哪个函数类型非常的类似?追问为什么类似正弦型函数(排除法,关键在于周期性)。
(学生活动,求解解析式)
得到的是一个刻画水深与时间关系的三角函数模型,为了保证所选函数的精确性,通常还需要一个检验过程,教师点明:建模过程——选模,求模,验模,应用。有了这个模型,我们大致可以知道哪些情况?学生小组合作讨论回答,如周期、单调性、每时每刻的水深。
【问题探究2】:一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
(师生一起分析)用数学的眼光看,这里研究的是一个怎样的数学问题?水深米得出,即,
(师生齐分析)解三角不等式的方法
令学生活动:操作计算器计算, 结合电脑 ( http: / / www. / " \t "_blank )呈现图象
发现:在[0,24]范围内,方程的解一共有4个,从小到大依次记为:
那么其他三个值如何求得呢?(学生思考)
得到了4个交点的横坐标值后,结合图象说说货船应该选择什么时间进港?什么时间出港呢?
(学生讨论,交流)
可能结果:【生1】货船可以在0时30分钟左右进港,早晨5时30分钟左右出港;或者是中午12时30分钟左右进港,在傍晚17时30分钟左右出港。
【生2】货船可以在0时30分钟左右进港,可以选择早晨5时30分,中午12时30分,或者傍晚17时30分左右出港。
……
(学生讨论,最后确定方案1为安全方案,因为当实际水深小于安全深度时,货船尽管没有行驶,但是搁浅后船身完全可以馅入淤泥,即使后来水位上涨,也很可能船身不再上浮)
刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随着船身自身重量的减小,船身会上浮,这样一来当两者都在改变的时候,我们又该如何选择进出港时间呢?请看下面问题:
【问题探究3】:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
(学生讨论)安全即需要:实际水深安全水深,即:
,
讨论求解方法:用代数的方法?几何的角度?(电脑 ( http: / / www. / " \t "_blank )作图并呈现)
通过图象可以看出,当快要到P时刻的时候,货船就要停止卸货,驶向深水区。那么P点的坐标如何求得呢?(学生思考,讨论,交流)求 P点横坐标即解方程
数形结合,二分法求近似解:
由图得点P点横坐标在[6,7],故我们只需要算出6,6.5,7三个时刻的安全水深与实际水深的数值表就可以回答上面的问题。
时间 实际水深 安全水深 是否安全
6.0 5米 4.3米 安全
6.5 4.2米 4.1米 较安全
7.0 3.8米 4.0米 危险
货船应该在6时30分左右驶离港口。(可能有的同学有些异议,可以讨论)
从这这个问题可以看出,如果有时候时间控制不当,货船在卸货的过程中,就会出现货还没有卸完,不得已要暂时驶离港口,进入深水区,等水位上涨后在驶回来。这样对公司来说就会造成才力、物力上的巨大浪费?那该怎么来做呢? (学生讨论)
可以加快卸货速度,也就是加快安全深度下降速度。
【问题探究4】:若船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,货物卸空后吃水深度为2米,为了保证进入码头后一次性卸空货物,又能安全驶离码头,那么每小时吃水深度至少要以多少速度减少?---探究3的变式(学生课后探究)
三、质疑答辩,排难解惑,发展思维
1.如图,单摆从某点给一个作用力后开始来回摆动,离开平衡位置O的距离s厘米和时间t秒的函数关系为.
(1)单摆摆动5秒时,离开平衡位置多少厘米?
(2)单摆摆动时,从最右边到最左边的距离为多少厘米?
(3)单摆来回摆动10次所需的时间为多少秒?
2.如图,某地一天从6~14时的温度变化曲线近似满足函数.
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
【问题的反思】:
①一般地,所求出的函数模型只能近似刻画这天某个时段的温度变化情况,因此应当特别注意自变量的变化范围;
②与学生一起探索的各种求法;(这是本题的关键!也是难点!)(用最大小值点代入不容易出现错误)
③如何根据图像求解析式中的待定参数
④探究其他解法:或 等
⑤借助三角函数模型研究的思想方法研究一些较复杂的三角函数。
四、巩固深化,反馈矫正
1.某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:小时)的函数,经过长期观察,该函数的图象可以近似地看成. 下表是测得的某日各时的浪高数据:
t(时) 0 3 6 9 12 15 18 21 24
y(米) 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
依规定,当浪高不低于1米时浴场才开放,试安排白天内开放浴场的具体时间段.
2.某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,记为y=,下面是某日水深数据:
t(时) 0 3 6 9 12 15 18 21 24
y(米) 10.0 13.0 9.9 7.0 10.0 13.0 10.1 7.0 10.0
经过长期观察,y=的曲线可以近似看成y=Asint+b的图象.
(i)根据以上数据求出y=的近似表达式;
(ii)船底离海底5米或者5米以上是安全的,某船的吃水深度为6.5米(船底离水面距离),如果此船在凌晨4点进港,希望在同一天安全出港,那么此船最多在港口停留多少时间?
教法:从表中读到一些什么数据? → 依次求各系数 → 应用模型解决问题
答案:(0≤t≤24); 13(小时).
小结:读取与分析表中的数据,是一种数学思维能力的训练. 求得模型后,把第(2)问的情景转化为一个简单的三角不等式,再运用整体思想,借助函数的图象或者单位圆可以求解.
3.某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试建立出厂价格、销售价格的模型,并求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数.
五、归纳整理,整体认识
从以上问题可以发现三角函数知识在解决实际问题中有着十分广泛的应用,而待定系数法是三角函数中确定函数解析式最重要的方法.三角函数知识作为数学工具之一,在以后的学习中将经常有所涉及.学数学是为了用数学,通过学习我们逐步提高自己分析问题解决问题的能力.
三角函数应用模型的三种模式:一是给定呈周期变化规律的三角函数模型,根据所给模型,结合三角函数的性质,解决一些实际问题;而是给定呈周期变化的图象,利用待定系数法求出函数模型,再解决其他问题;三是搜集一个实际问题的调查数据,根据数据作出散点图,通过拟合函数图象,求出可以近似表示变化规律的函数模型,进一步用函数模型来解决问题.
回顾整个探究过程,经历了第一阶段:收集数据-----画散点图
第二阶段:根据图象特征---选模、求模、验模
第三阶段:函数模型应用
在整个探究过程,我们用到数学常见的一些思想方法:
(1)对实际问题处理过程是,首先是挖掘其中的数学本质,将实际问题转化为数学问题;体现了数学中的转化思想;
(2)在对一些数据处理的过程用到了估算的思想;
(3)在用代数方法处理困难的一些题目的解决中,用到了数形结合的思想;
(4)在方程的求解过程中,用到了算法中“二分法”思想。
六、承上启下,留下悬念
七、板书设计
八、课后记:
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
